不同介質下不耦合裝藥爆破ALE空間范圍的研究

黃瑞彬, 吳 磊

(西南交通大學土木工程學院, 四川成都 610000)

數值模擬作為一種經濟有效的研究方法，被廣泛應用于各種工程領域。對于爆炸動力學問題，由于其過程的復雜性、作用時間的短暫性，實際試驗的危險性，使數值模擬成為研究該類問題不可或缺的手段。利用LS-DYNA，可以模擬爆炸的整個過程并再現爆炸過程中產生的應力波和沖擊波，已經解決了許多實際工程上的問題。在LS-DYNA中模擬爆炸問題有幾種常見的方法：拉格朗日方法，歐拉法，多物質ALE流固耦合法[1]。其中拉格朗日方法炸藥和結構采用共節點或設置滑移接觸，其優點是計算時間短，與爆炸實際比較符合，并具有清晰的物質界面，但網格會產生較大畸變，常導致負體積，導致計算中止。歐拉法的空間網格不動，材料網格可以在空間網格中流動，這樣就解決了網格畸變的問題，其缺點是物質界面模糊計算時間長。多物質ALE流固耦合法綜合了上述兩種算法的優點，炸藥等采用ALE算法，結構采用Lagrangian算法，兩者之間定義流固耦合關系，在許多研究成果中被采用。

諸多學者都對LS-DYNA模擬計算的影響因素進行了研究，李利莎[4]等人分析了Lagrange、ALE和SPH三種算法的接觸爆炸模擬計算的優缺點。鄧麗梅[5]等人研究了方型藥包ALE空間的大小對數值分析的影響；黃佑鵬[6]等人研究了不同裝藥半徑，不耦合系數和網格精度條件下流固耦合范圍對計算結果的影響。

模擬不耦合裝藥爆破常采用多物質ALE流固耦合法，該方法的一個特點就是需要建立一個炸藥可能膨脹的ALE空間網格與被爆炸物網格重疊[2]。因為炸藥爆炸膨脹會超過物質邊界，其目的就是為炸藥物質的運動提供流動空間。在諸多采用流固耦合法模擬的不耦合裝藥爆破的研究成果中，對于流固耦合法的ALE空間提及不多，對它的大小如何取值以及不同介質對其的影響研究較少，而ALE空間的耦合范圍決定了網格數量的多少，對整個數值模擬計算特別是大型3D模型的時長和精度有著比較顯著的影響：耦合范圍過小，計算結果不準確，耦合范圍過大，計算時間增大，而不耦合裝藥爆破模擬過程中又常出現空氣介質和水介質[3]，因此有必要研究不同介質條件下不耦合裝藥爆破的最小ALE空間耦合范圍取值。

本文采用LS-DYNA進行大量數值計算，討論了3種不耦合系數(K)下空氣和水介質條件下ALE空間耦合范圍(R)對于爆炸結果的影響，并進行了誤差分析，得出了對于不耦合裝藥爆破，在同一藥徑下，空氣和水介質條件下分別的最小合理耦合范圍Rmin取值，對比了不同介質之間Rmin的差異，為相關不耦合裝藥爆破的數值模擬提供參考。

1 模型的建立

模型由炸藥，不耦合介質(空氣或水)，巖體部分組成，由于需要進行多次大量數值模擬計算，為節約計算量，模型采用單層的實體網格模型進行數值模擬分析[7]。炸藥空氣水介質均采用多物質ALE算法，巖石采用拉格朗日算法，它們之間采用流固耦合，所有計算均采用cm·g·μs單位制。

模型尺寸為300 cm×300 cm×1 cm,裝藥長度為220 cm,炸藥直徑為40 mm,位于模型中心。ALE空間采用空氣材料，耦合區域半徑(炸藥中心到ALE空間網格邊緣)為R，前后面設置約束條件，左右和下邊界進行無條件反射設置，起爆點設置為炸藥中心，如圖1所示。

圖1 模型示意

2 材料及狀態方程

模型中涉及到的材料包括：炸藥，空氣，水，巖石。其中炸藥空氣水都采用多物質ALE算法，巖石采用拉格朗日算法，炸藥采用MAT_HIGH_EXPLOSIVE_BURN材料和JWL狀態方程描述描述,相關參數為[8]：

ρ0=1.09g/cm3,D=0.43cm/μs,Pcj=4.36GPa,A=214,B=0.182,R1=4.2,R2=0.9,θ=0.15,E0=4.192。

空氣采用MAT_NULL材料和EOS_LINEAR_POLYNOMIAL狀態方程，水采用EOS_GRUNEISEN狀態方程。空氣材料參數：ρ0=1.09g/cm3,C0=-1e-6,C4=0.4,C5=0.4,E0=2.5e-6。

水材料參數：ρ0=0.998g/cm3,C=0.165,S1=1.921,S1=-0.096,θ=0.35,E0=2.89e-6。

巖石采用JHC模型材料描述，相關參數見參考文獻[9]。

采用CONSTRAINED_LAGRANGE_IN_SOLID關鍵字定義ALE流固耦合作用，NQUAD=3,其他參數采用缺省值。

3 模擬結果

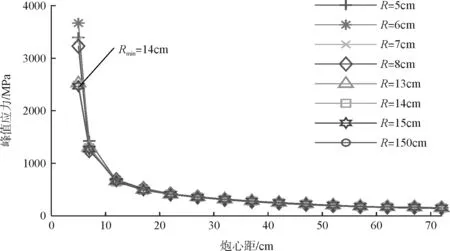
在保證ALE空間網格重至少與巖體網格重疊1 cm的條件下，進行大量不同耦合半徑的數值模擬。從炮孔壁中心處附近開始依次每隔5 cm取一個測點，圖2分別給出了不耦合系數為K=2、3、4，空氣和水介質條件下峰值應力衰減曲線隨耦合半徑變化情況。可以看出：不管是在空氣還是水介質條件下，耦合半徑R對于計算結果的影響主要是集中在炮孔近區特別是孔壁附近(峰值應力絕對誤差超過50 %)，對遠區幾乎沒有影響(峰值應力絕對誤差不超過5 %)，故重點討論孔壁處峰值應力的變化。

如圖2(a)，圖2(b)所示：當K=2時，空氣介質條件下，孔壁處峰值應力有較大差異，在達到最小合理耦合半徑前，孔壁峰值變化不穩定，最大可達到3 670 MPa，R越小，孔壁處峰值變化應力越大，耦合范圍R對其他點處的峰值應力幾乎沒有影響，從總體來看，峰值應力衰減曲線隨著R的增大而逐漸收斂，當R增大到14 cm時，即最小耦合半徑Rmin=14cm，曲線已經收斂，孔壁處的峰值應力穩定到2 469 MPa左右，繼續增大R應力衰減曲線基本一致，各點峰值應力誤差不超過5 %，衰減曲線已經收斂并保持穩定；水介質條件下，峰值應力在達到最小合理耦合半徑前峰值應力的不穩定性相比于空氣條件下增加，且不僅影響孔壁處的應力峰值，還會影響炮心距15 cm范圍內計算點的峰值應力，隨著不耦系數的增加影響范圍擴大到30 cm左右，R越小，孔壁處峰值應力越小，最小值只有2 385 MPa，隨著R的增大，孔壁處峰值應力增大，隨后穩定到4 285 MPa左右。當R增大到23 cm時，曲線收斂。

(a)空氣介質：K=2

如圖2(c)，圖2(d)所示：K=3時，空氣介質條件下，耦合半徑達到最小耦合范圍Rmin=22cm，孔壁處峰值應力穩定在1 999 MPa左右;水介質條件下，最小耦合范圍Rmin=35cm，孔壁處峰值應力穩定在2 803 MPa左右，峰值應力衰減曲線重疊趨于一致。

如圖2(e)，圖2(f)所示：K=4時，空氣介質條件下，耦合半徑達到最小耦合范圍Rmin=31cm后,孔壁處峰值應力穩定在1 640 MPa左右;水介質條件下，耦合半徑達到最小耦合范圍最小耦合范圍Rmin=49cm，孔壁峰值應力穩定在2 398 MPa左右，峰值應力衰減曲線重疊趨于一致。

為驗證最小耦合半徑Rmin準確性，取K=2時，分析空氣介質和水介質條件下200 us時的應力云圖。結果顯示,空氣介質條件下,耦合半徑R=14cm,應力云圖開始穩定；水介質條件下，耦合半徑R達到23 cm應力云圖開始穩定，如圖3所示。

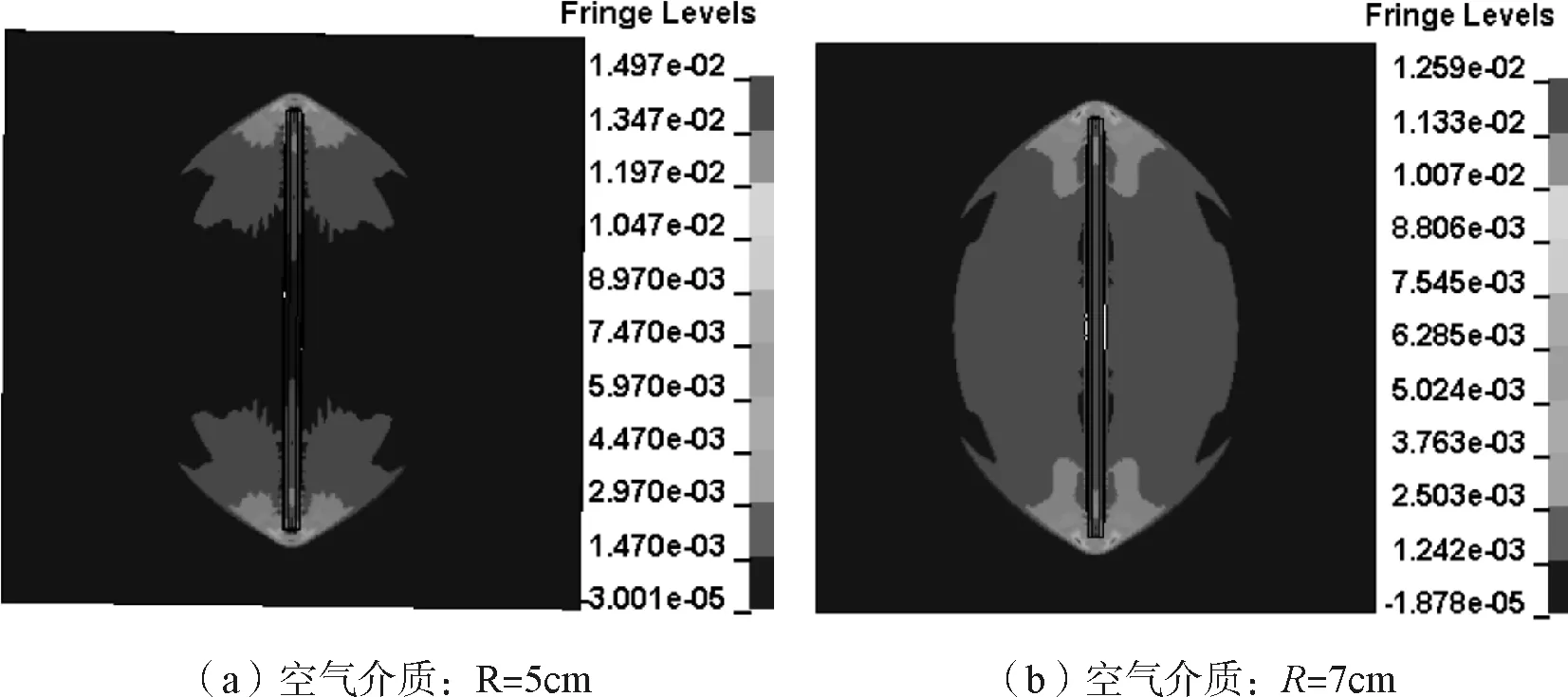
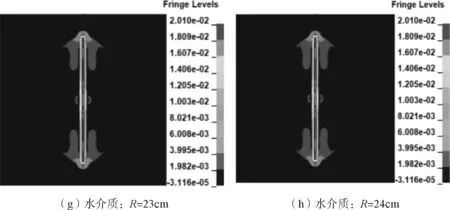
圖3 不同介質下200us應力云圖

4 結論

(1)通過對峰值應力衰減曲線的分析，ALE空間耦合范圍對模擬結果的影響主要是在炮孔近區，特別是孔壁處影響較大，對遠區幾乎沒有影響。

(2)同一藥徑下，相比空氣介質條件，水介質條件的最小耦合半徑Rmin更大，大約是空氣介質條件下的1.6倍左右。空氣介質條件下Rmin取值為7～16 cm，水介質條件下取值為12～25 cm(不耦合系數大取小值，不耦合系數小取大值)。故在有水條件下，建議適當增加流固耦合范圍。

(3)隨著不耦合系數的增大，耦合半徑對于結果的影響逐漸減小，當不耦合系數較大時，耦合范圍應適當增加。

(4)在較小的耦合范圍內，炮孔近區峰值應力和應力云圖不穩定，空氣介質條件下的峰值應力較大，水介質條件下的峰值應力較小，且水介質條件下的不穩定性較大，隨著耦合范圍的增大，應力云圖高應力區增加，峰值應力與應力云圖逐漸穩定并趨于一致。

(5)對于大型3D模型而言，ALE空間耦合范圍的選擇尤為重要，過大會使網格數量成倍增加，影響計算效率，過小會使計算結果不準確。