機組非停擾動下PSS調節性能評估及參數校核
孟凡超,胡文平,劉翔宇
(國網河北省電力有限公司電力科學研究院,河北 石家莊 050021)
0 引言
隨著遠距離大容量輸電系統的不斷發展,電力系統穩定問題日趨復雜。暫態穩定呈現出了新的特點,動態穩定、電壓穩定問題均日益嚴重,特別是以低頻振蕩為代表的小干擾穩定問題,對電網穩定的影響越來越突出[1-3]。
在低頻功率振蕩的抑制措施中,電力系統穩定器(PSS)具有概念清晰、結構簡單、效果良好等優點,在國內外得到了廣泛應用。作為同步發電機的一種附加勵磁控制,PSS主要是通過在勵磁電壓調節器中引入領先于軸角速度的附加信號,增加系統的正阻尼轉矩來實現對低頻振蕩的抑制。目前為止,PSS仍然是阻尼局部功率振蕩最經濟有效的措施。深入研究低頻振蕩的產生機理,結合工程現場實際系統地研究PSS參數對低頻振蕩抑制效果的影響以及PSS參數的優化整定方法,具有重要的學術價值和實際工程意義[4]。
至今,無論是在理論還是實踐中,PSS參數整定已有眾多的方法和技術。這些方法總體上分為兩大類[5],一類是現場試驗法,即在機組運行中,通過測試機組及其勵磁系統的開環響應特性,進而設定PSS控制參數;另一類是模型分析法,即通過機組和電網的數學模型,通過理論推導或時域仿真來設計和校驗PSS參數。現場測試法的局限在于只能在機網少數運行方式和振蕩模式情況下整定和驗證PSS控制參數;模型分析法的缺陷在于模型的準確性存疑。
考慮到實際電網的不斷演變以及運行方式多變性,PSS實際控制效果如何,就成為十分重要的問題。但長期以來,缺乏一套對PSS 抑制低頻振蕩的實效進行在線評估的手段[6]。火電機組是一個包括鍋爐、汽輪機、發電機的復雜發電系統,由于鍋爐泄漏、汽輪機振動、熱工保護動作、廠用電系統故障等原因引起的機組非計劃停運(簡稱“非停”)時有發生。基于WAMS系統數據,利用非停機組對在運機組的大擾動,提出一種在線評估PSS調節性能的方法[7]。
1 PSS性能評估方法的相移原理
PSS性能評估的基本原理見圖1。
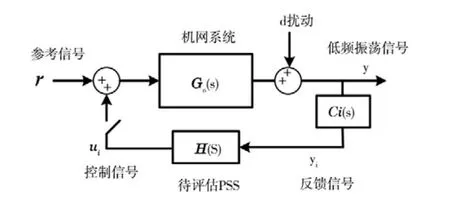
圖1 PSS性能評估的基本原理
如圖1所示,當待評估PSS未投運時,稱為開環系統,而當待評估PSS投運時,稱為閉環系統。設d為系統等效擾動,y o(y c)為開環(閉環)系統在受到擾動后產生的能代表系統低頻振蕩特性的動態響應信號,y i,u i為PSS的反饋信號和控制輸出信號,G o(s),H(s)分別為開環系統和待評估PSS的近似線性化系統傳遞函數,各信號之間的關系如下:

當PSS投入閉環運行時,按照線性疊加原理,則有:
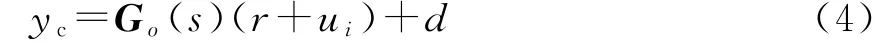
將式(2)-(3)代入式(4),則有:
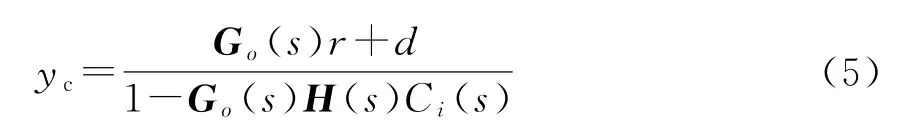
對于抑制低頻振蕩而言,目標是使得功率波動趨向于0,即r=0,進而有:
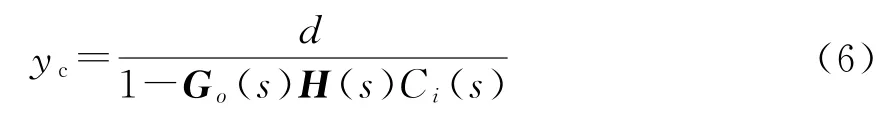
當系統發生擾動,導致某一模態出現功率振蕩時,可令s=jω表示角頻率為ω的功率振蕩,則該振蕩模態的動態過程可近似描述為:
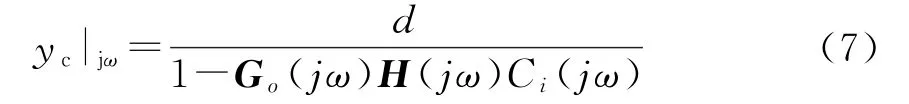
對于特定的系統運行方式,即G o(jω),C i(jω)一定的條件下,如果PSS的增益固定(受限于控制能量約束),則可知:對于頻率為ω的振蕩模式,PSS相移滿足以下條件時:
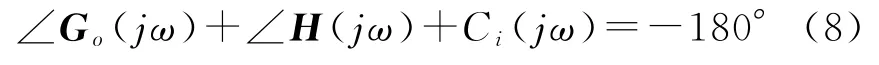
其振蕩的幅值最小;換言之,該模式對于擾動有最好的魯棒穩定特性;而且PSS的相移特性越接近于滿足式(8),對應模式的振蕩幅值越小。因此,可以通過在線分析PSS輸入-輸出的相移特性來檢驗PSS的效用,考慮到信號的偏差,設置相移區間為150°~210°,這就是在線評估PSS 的相移原理。
2 仿真分析
2.1 仿真分析系統
2.1.1 機組-電網模型
為驗證機組非停工況下PSS調節性能,本節采用實際電網離線數據進行仿真分析。離線數據中的發電機、勵磁系統、PSS、調速系統均按照實際電網模型建模,參數為工程實測參數,少數未實測機組采用典型參數,采用BPA 軟件計算不同負荷水平時機組非停故障下PSS的調節性能。
2.1.2 勵磁系統與PSS的模型及參數
機組勵磁系統AVR 具有IEEE ST1A 標準模型,其傳遞函數如圖2所示。
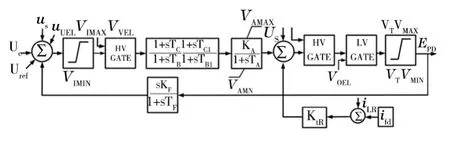
圖2 IEEE ST1A 靜態勵磁系統
AVR 的典型參數為:TC=3 s,TB=4 s,TB1=0.06 s,TC1=0.03 s,KF=0,TF=1 s,KA=56.25,TA=0.02 s。
機組的PSS 具有IEEE PSS2B 標準模型,其傳遞函數如圖3所示。
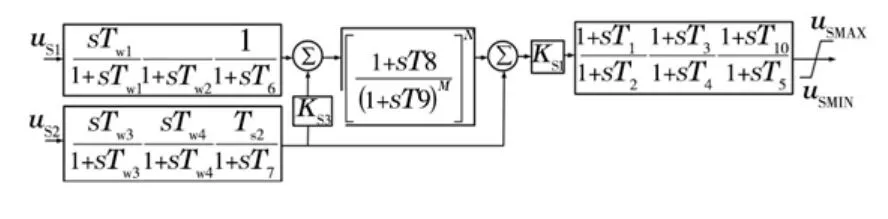
圖3 IEEE PSS2B雙輸入電力系統穩定器
PSS的典型參數為:Ks1=7,Ks2=6.8,Ks3=1.2,T1=0.05 s,T2=0.19 s,T3=0.05 s,T4=0.19 s,T4=0.1 s,T5=0.1 s,T10=0,T6=0.2 s,M=2,N=1,Tw1=6 s,Tw2=6 s,Tw3=6,Tw4=6 s,T7=6 s,T8=0.6 s,T9=0.09 s;圖中us1代表以轉速偏差作為系統的反饋量,us2代表以功率偏差作為系統的反饋量,在本例中只取功率作為系統的反饋量。
2.2 仿真分析結果
在PSS參數確定的情況下,機組非停工況下PSS調節性能與勵磁系統無補償特性密切相關。而勵磁系統無補償特性對并列機組數量、并網電氣距離、電網負荷水平、臨近機組PSS投退等因素不敏感,對機組有功、無功出力影響顯著[8]。本節僅對不同有功功率、無功功率情況下PSS的調節性能進行仿真分析。選取某發電廠作為研究對象,安裝有2 臺機組,其發電機額定有功功率為330 MW,額定無功功率為160 MVar。
2.2.1 機組額定有功功率時PSS性能分析
保持運行方式不變,發電機遲相運行,在有功功率為330 MW,無功功率為160 MVar工況下,切除1 號機組,分析2 號機組PSS 的調節性能。額定有功功率非停時機組仿真曲線見圖4。
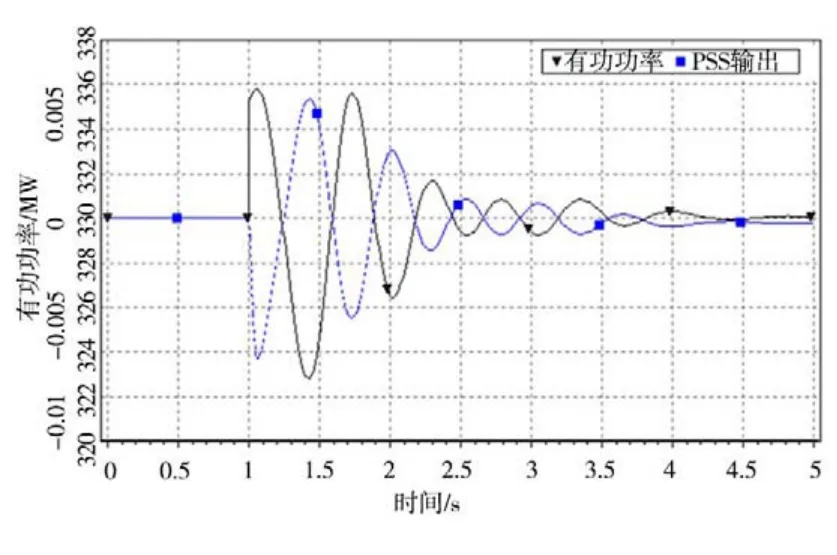
圖4 額定有功功率非停時機組仿真曲線
由圖4可知,有功功率振蕩次數為3次,振蕩頻率為1.52 Hz,阻尼比為0.12,滿足標準要求。此時有功功率第1次最大值時間為1.06 s,PSS輸出第1次最大值時間為1.43 s,兩者的相位差為201°,滿足PSS相移區間的設定。
2.2.2 機組50%額定有功功率時PSS性能分析
保持運行方式不變,發電機遲相運行,在有功功率為165 MW,無功功率為80 MVar工況下,切除1 號機組,分析2 號機組PSS 的調節性能。50%額定有功功率非停時機組仿真曲線見圖5。
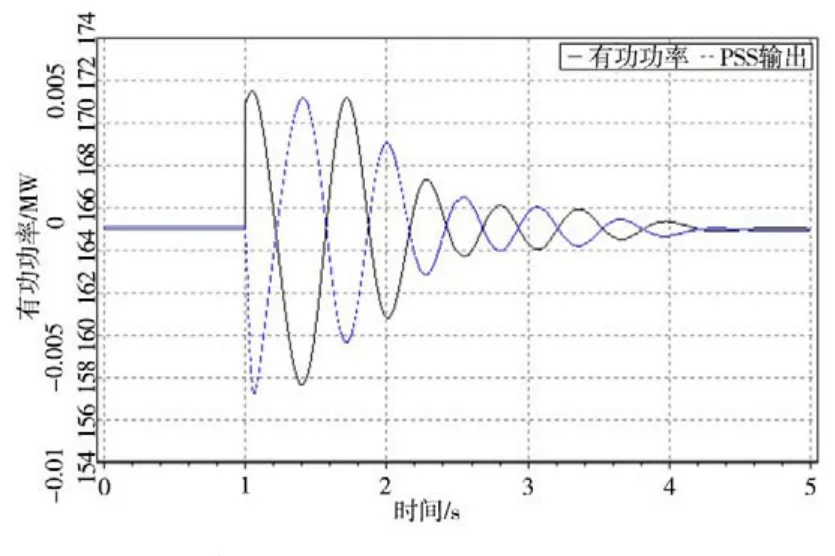
圖5 50%額定有功功率非停時機組仿真曲線
由圖5可知,有功功率振蕩次數為3次,振蕩頻率為1.49 Hz,阻尼比為0.11,滿足標準要求。此時有功功率第1次最大值時間為1.05 s,PSS輸出第1次最大值時間為1.41 s,兩者的相位差為193°,滿足PSS相移區間的設定。
2.2.3 發電機進相時PSS性能分析
保持運行方式不變,發電機進相運行,在有功功率為165 MW,無功功率為-45 MVar工況下,切除1 號機組,分析2 號機組PSS 的調節性能。額定有功功率非停時機組仿真曲線見圖6。
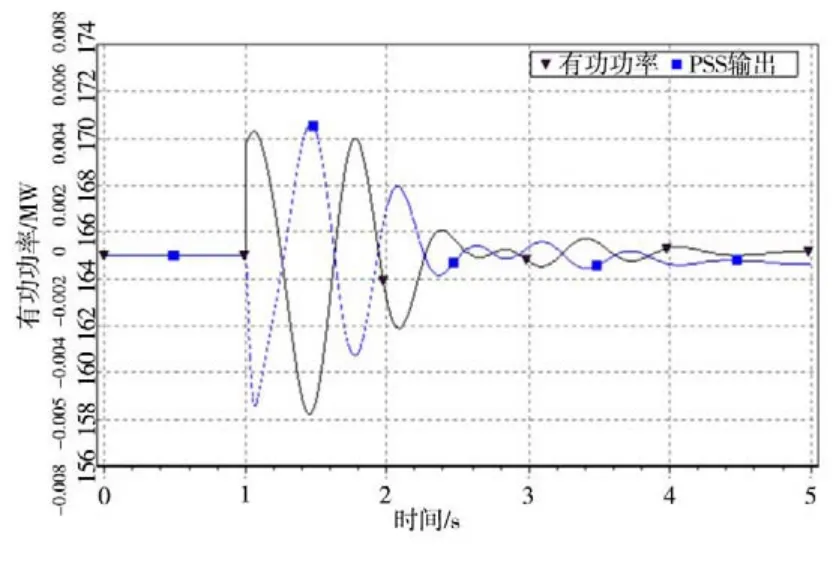
圖6 額定有功功率非停時機組仿真曲線
由圖6可知,有功功率振蕩次數為3次,振蕩頻率為1.39 Hz,阻尼比為0.13,滿足標準要求。此時有功功率第1次最大值時間為1.06 s,PSS輸出第1次最大值時間為1.46 s,兩者的相位差為200°,滿足PSS相移區間的設定。
在發電機額定有功功率、50%額定有功功率、發電機進相3種負荷水平時,機組非停擾動下對PSS調節性能進行了分析,當有功功率與PSS輸出相位差在設定的PSS相移區間時,PSS的調節性能滿足標準要求,能夠有效抑制低頻振蕩。
3 PSS性能評估的工程應用
3.1 機組非停概況
2019年3月4日11:16,河北省南部電網某熱電廠1號機組跳閘,機組容量330 MW,原因為汽輪機DEH 主蒸汽閥門及調門異常關閉,汽包壓力升高,汽包水位低保護動作切機。機組非停前,全網統調發購25 236 MW,1號機組故障前出力260 MW,占河北省南部電網統調發購的百分比為1.03%。由電氣專業的發變組A 柜逆功率跳閘,24 ms后主斷路器跳開,88 ms后滅磁斷路器跳開,機組與系統解列。
3.2 PMU 裝置錄波分析
1號機組非停過程中,PMU 裝置錄取的2號機組的有功功率及PSS輸出信號。正常情況下有功功率和PSS輸出信號均出現小幅波動,有功功率波動為249~251 MW,波動幅值為2 MW,PSS輸出信號波動為0~0.1 V,波動幅值為0.1 V。在11:14:19時,1號機組跳閘,2號機組有功功率和PSS輸出信號均出現大幅波動。有功功率波動為247~253 MW,波動幅值為6 MW,PSS輸出信號波動為-0.4~0.3 V,波動幅值為0.7 V。有功功率波動幅值擴大3倍,PSS輸出信號波動幅值擴大7倍。有功功率和PSS輸出信號相位差為162°,在PSS的有效相移區間內,PSS參數能夠有效抑制本次低頻振蕩。
3.3 PSS性能試驗驗證
由于受到現場試驗條件的限制,僅對本機振蕩頻率的PSS阻尼效果進行了驗證。發電機并網運行,發電機有功功率為300 MW,無功功率為80 Mvar,PSS退出,將發電機TV 及TA 二次側三相電壓和三相電流接入WFLC電量分析儀中準備錄波,在此情況下進行負載電壓2%階躍試驗,同時啟動WFLC 錄波,記錄有功功率的擺動次數。再將PSS投入,同樣工況下重復以上試驗。
PSS不投入時,有功功率擺動次數約為4次;PSS投入后,有功功率擺動次數約為1次。由此可知,有功功率的擺動次數減少,PSS對于本機振蕩有明顯的抑制作用。
4 結論
通過理論分析、仿真計算和現場試驗相結合的方法,研究了基于WAMS系統數據的機組非停擾動下PSS調節性能的評估和參數校核方法。得出如下結論:
a.通過在線分析PSS輸入-輸出的相移特性即有功功率與PSS輸出的相位差能夠檢驗PSS的效用,相移可以設為150°~210°;
b.依據PSS輸入-輸出的相移特性評估PSS參數與進組有功功率、無功功率等因素不敏感;
c.經機組故障跳閘后WAMS系統數據的分析證實了應用PSS輸入-輸出的相移特性評估其參數切實可行。

