線型聚能切割爆破的理論研究

李曉杰，閆鴻浩，王小紅，王宇新

(1.大連理工大學運載工程與力學學部工程力學系，遼寧 大連 116024; 2.工業裝備結構分析國家重點實驗室，遼寧 大連 116024)

線型聚能爆炸切割是在1888年C.E. Munroe發現空穴裝藥聚能效應之后，在空穴裝藥基礎上1894年又提出的聚能爆破技術，現已廣泛用于軍事、民用爆破工程等領域中。如：火箭的級間分離、導彈出倉、破甲彈和魚雷等戰斗部、地雷、工兵爆破裝置等大型軍事裝備[1-3]，對飛機艙體、艙蓋、防盜門、墻壁、大巴車等開設應急通道[4-6]，以及拆除鋼筋混凝土、切割鋼結構、采石、隧道掘進、邊坡預裂、油氣井施工、海洋油井與平臺拆解等工程爆破[7-17]。由于聚能爆炸切割問題的三維復雜性，所以開始一直沿用二維流體聚能破甲理論[18]。隨著科技發展，至上世紀70～80年代人們逐步提出了聚能切割的三維流體理論[19]。但由于涉及軍事原因，各國的研究幾乎都是獨立進行的，資料交流很少。在此期間，我國也開始了三維聚能切割理論研究[20-22]，并發展了準定常理論和切割器最佳頂角等原理，并指導了工程應用。近年來，隨著計算技術的發展，尤其是無網格方法進入到大型爆炸問題的研究后，人們開始對采用二維、三維模型對爆炸切割問題進行研究[23-28]，并對其原理認知更加清晰。本文通過建立聚能切割的三維不可壓縮流體模型，推導出聚能射流參數關系，并結合聚能破甲理論，對爆炸切割器的設計要點進行了分析。系統地說明了線型聚能爆破的切割深度、切割器炸高、聚能罩最佳頂角、聚能罩材料及其與切割器參數的關系、切割器裝藥量的選取原則，以及各種爆轟方式對切割能力的影響等。文章在理論分析過程中，盡量采用簡潔直觀的方法推導，著重物理概念的闡述與分析，作為基本理論研究，以期對爆炸聚能切割器的設計與應用起到促進作用。

1 線型聚能切割器理論

1.1 端部起爆的線型聚能切割理論解

圖1 線型聚能切割的立體透視Fig.1 Stereoscopic perspective of linear shaped-charge cutting

為了更清晰地分析聚能罩碰撞、射流和杵體的關系，現將切割器橫截面I與碰撞對稱面xy上的圖像繪制在一起，如圖2所示。圖2a中聚能罩母線的O′A′顯然對應面II上的OA，長度為h。A′B′為聚能罩邊緣的飛行距離，應與O′A′相垂直。定義A′B′方向的坐標為y′，弧長坐標為s，如圖3所示。

圖2 線型聚能切割(截面)Fig.2 Linear shaped-charge cutting(section)

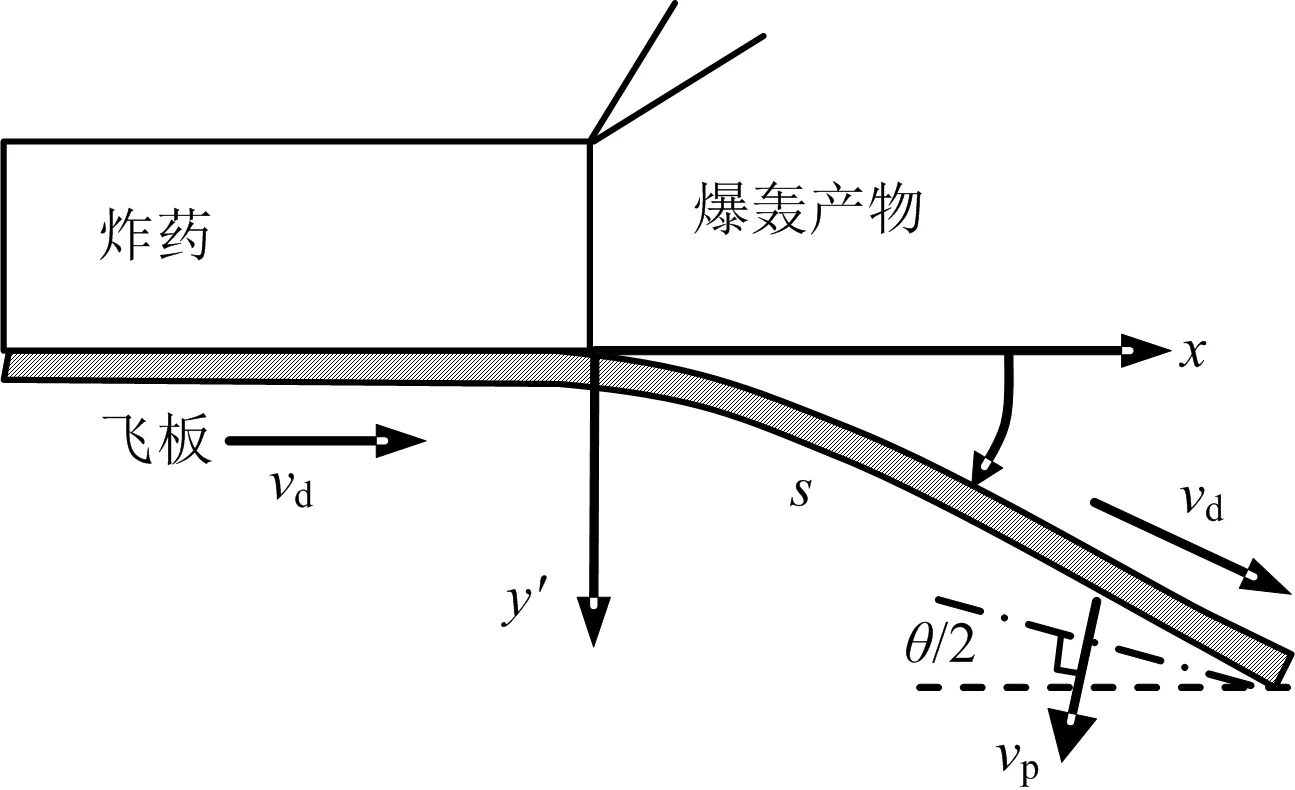
圖3 滑移爆轟驅動飛板運動Fig.3 Plate flyer driven by sweeping detonation

根據滑移爆轟驅動平板的原理，令彎折角為θ，有：

(1)

在θ角為常數時，有：

y′=x·tgθ；y′=s·sinθ

(2)

再回到圖2a可見，A′B′長度即是y′, 圖2b中的GB即是x, 可有：

A′B′=h·tgφ=GB·tgθ?GB=

h·tgφ/tgθ

O′B′=h/cosφ=OG

H=O′B′-h·cosφ=(h·sinφtgφ-h·cosφ)

(3)

圖2b中注意OG和GB的三角關系，可得：

tgβ=OG/GB= tgθ/sinφ

(4)

再根據聚能罩流速與杵體的流速相等，在同一時間流動長度也相等，可得到圖1中的AB是流動的弧長s，必然與圖2b中的OK和OF相等，則可得：

再與射流刀、杵體刀寬度為h的三角關系：

得到：

tg (α-β)=tg (β-ψ)=sinθ/tgφ

(5)

將上式用正切和角公式打開，并將式(4)代入，經整理可得：

(6)

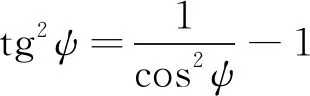
(7)

再用半角公式cosψ=1-2sin2(ψ/2)代入上式，求解得：

(8)

進一步從圖3飛板運動關系還可以得到，飛板的對地拋擲速度方向是垂直于θ角平分線的，其速度vp值可用Taylor公式計算：

vp=2vdsin (θ/2)

(9)

如果把Taylor公式推廣用于描述杵體與射流，也可見杵體與射流的對地拋擲速度是分別垂直于ψ和α角平分線的，速度值分別為

(10)

將式(8)代入(10)，可得：

(11)

由于切割器罩體被炸藥拋擲碰撞后分成了射流與杵體，碰撞前后動能是守恒的。故設切割器罩體單位面積質量為m, 射流為2mj，則杵體質量為2(m-mj)，有如下能量關系：

將式(8)、式(9)、式(11)代入上式，可得：

2mj/m=1-cosθcosφ

(12)

至此，已經完全得到了一端起爆的聚能線型切割器的射流與杵體的理論解。射流與杵體為與聚能罩等寬的刀片狀流體，射流質量為式(12)的2mj，杵體質量為2(m-mj), 分別以式(11)中的vpj和vps速度，以垂直于α和ψ角平分線方向對地運動，射流與杵體的彎折角α和ψ可用式(6) ～式(8)計算。

1.2 刀狀聚能射流對靶板的切割

1.1節討論了聚能切割器形成刀片狀射流的理論解，下面探討聚能射流切割靶板問題。

1)切割深度。寬度h的刀片狀射流以彎折角α斜碰撞在靶板上，并以速度vd沿-x方向水平移動，射流相對靶板的速度為vpj與寬度方向呈α/2夾角。當把動坐標放置在碰撞點上，以vd速度隨動時，可見如圖4所示的定常流動圖像。

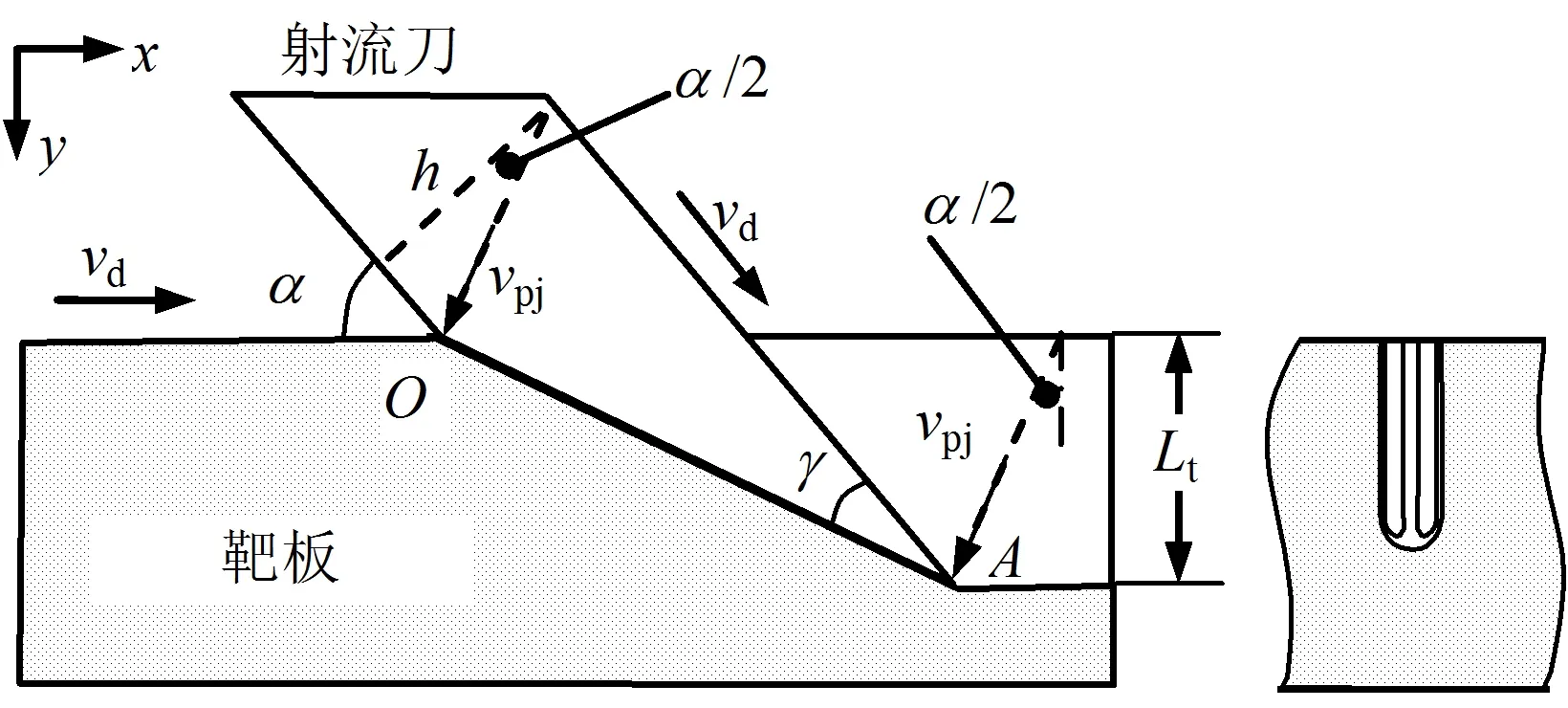
圖4 聚能射流刀片切割靶板Fig.4 Target slab cut by a shaped charge jet blade

從圖4可見，射流在vpj方向的寬度為h/cos(α/2)，在該方向的切割深度為Lt/cos (α/2)，根據定常射流破甲理論公式，有：

(13)

式(13)即為切割器流體破甲深度公式。式中：ρt和Lt為靶板密度和切割深度；ρ和h為聚能罩密度和可用邊長，h也是射流刀的寬度。對于考慮靶板強度的定常破甲深度，也可采用如下公式：

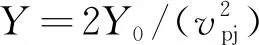
2)炸高。聚能切割器的橫截面(見圖2)的幾何關系得到式(3), 可以寫為

H/h=sinφtgφ

(14)

式(14)即為聚能切割器的理論炸高H的計算式。炸高小于該式計算值，則聚能罩邊緣在碰撞匯聚之前就會撞擊到靶板上，造成浪費；炸高高于該式值，聚能罩則可完全利用；但炸高過高時，片狀射流可能會波動分散，使切割能力下降。

3)聚能罩最佳頂角。聚能切割器產生的射流是傾斜入射在靶板上的。實際上主要起破甲作用的是射流垂直向下y方向的分速度，水平x方向的速度應該是一種浪費。另外，如果射流y方向的速度很高，射流質量很小是對切割無宜，故選用y方向射流的速度與質量組合的能量作為切割能力的評價指標。先計算射流y方向的速度：

則由上式和式(7)、式(8)、式(12), 可得射流動能為

(15)

將上式對φ求導，并令導數?E/?=0，可求得E的極值條件：

注意cosφcosθ≤1，故上式取負號，E的極值條件即為

cosφ=(1-sinθ)/cosθ

(16)

式(16)經驗證為射流動能E的極大值條件。在爆炸切割時，聚能罩拋擲角θ在15°～25°之間，以上式計算得到2φ在80°～101°之間，故式(10)可作為確定聚能罩最佳頂角2φ的條件。

使用式(15)和式(16)計算的射流y方向速度vjy及能量E與φ的關系如圖5所示，可見射流的vjy速度在φ=20°附近達到最大值vd，在最佳頂角附近下降到(0.6～0.8)vd, 該vjy也是隨θ角而增加的。由于爆炸切割一般都采用高能炸藥，爆速在6.0～7.5 km/s左右，因此，即便是vjy下降到0.6vd也在3.6 km/s以上，對于靶板仍有足夠的切割能力。但在該點之后vjy隨φ的下降幅度較快，所以在切割器設計時，頂角φ不應大于最佳頂角過多，以免vjy下降造成切割能力下降。

圖5 射流垂向速度、能量與φ 角的關系Fig.5 Relationship of jet vertical velocity, energy and φ

4)聚能罩材料。由圖2可見，由碰撞棱流出的射流與杵體都是vd流速的。那么可以想見，入射與兩股出流沿碰撞棱方向的流速分量是連續的，垂直與碰撞棱的流速分量才是發生碰撞的，這個分量值就是碰撞的來流速度vf。從圖2求取射流垂直流出碰撞棱的速度分量，并利用式(5)和三角函數關系，可得：

(17)

由于vf才是主導產生碰撞射流與杵體的流速，所以聚能罩材料屬性對流速vf有一定的要求。 作為出流條件，要求vf小于材料聲速，且使駐點壓力遠高于聚能罩材料強度，即：

(18)

式中:Rm為材料強度;N為比強度倍數，按爆炸焊接強度限，可產生射流時N=10，要順利產生射流N在20以上。退火軟銅的抗拉強度Rm在0.22 GPa左右，密度8.93 g/cm3，取N=10時，vf≥0.70 km/s; 取N=20時，vf≥0.99 km/s。采用普碳鋼Q235作為聚能罩時，Rm在0.40 GPa左右，密度7.85 g/cm3，取N=10時，vf≥1.01 km/s ; 取N=20時，vf≥1.43 km/s。

以式(17)并取爆速vd=6.0 km/s繪制的碰撞流速vf與切割器半頂角φ的關系如圖6所示。由圖可見，材料的出流限制會影響切割器參數設計。當采用vf=1.0 km/s為低限時，切割器半頂角φ的最大值在55°～70°；當采用vf=1.5 km/s為低限時，半頂角φ的最大值在45°～60°。對于聲速限制，純銅體波聲速為3.91 km/s，半頂角φ下降到25°時就已經接近聲速了。如果使用鉛作為聚能罩時，鉛合金體波聲速在2.0 km/s左右，半頂角φ就需要在35°～50°以上了。

圖6 切割器碰撞流速vf與φ 的關系Fig.6 Collision flow velocity vfvs φ of cutter

2 線型聚能切割的其他問題

線型聚能切割器的常用起爆方式是一端起爆，依靠滑移爆轟驅動聚能罩。但滑移爆轟驅動飛板的加速能力并不強，因此人們也在想法以各種方式來提高聚能切割器的切割能力。

2.1 切割器的頂部同步起爆

線型聚能切割器要完全實現頂部同步起爆是非常困難的，盡管可以使用平面波發生器，但在實際工程中可行性較低。研究頂部起爆，主要是針對較長的線型聚能切割器中部起爆時，研究其起爆點下方的運動行為(見圖7)。當聚能切割器在頂部引爆后，爆轟波沿聚能罩向下傳播，聚能罩被壓垮，以彎折角θ斜碰撞在對稱面O′B′上，并產生向下的射流。顯然，聚能罩在對稱面上的碰撞角為(θ+φ), 可以由此計算射流和杵體質量。

圖7 頂部起爆的聚能切割器Fig.7 Shaped charge cutter initiated on top

聚能罩運動的三角關系如圖8所示。從O點爆轟到點A，爆速為vd，行走距離OA; 碰撞點從O移動到B點，速度是vc，行走距離OB；原來的飛板OA變成了AB，減少的長度OB′=SB=OA-AB全部碰撞到對稱面上，這個飛板縮短的速度就是vf；在對稱面上從B點沖出的射流長度BJ應與飛板縮短量OB′相等，則射流與B點的相對速度也是vf，射流的絕對速度就是vj=vc+vf。再者,由已經撞擊的飛板長度OB′與射流長度BJ相等，得到射流長度即等于罩邊長h。杵體是已經撞擊的飛板長度SB=OB′，比OB短，所以多出的長度OS=OB-OS就是由杵體前移造成的；不用過多計算，注意速度是單位時間內的行走長度，即可得杵體運動速度vs=vc-vf。

圖8 頂部起爆切割器的碰撞關系Fig.8 Collision relationship of shaped charge cutter initiated on top

再按圖8中的三角關系，用正弦定理，有：

根據上式進行推導，可求出頂部起爆線型聚能切割器的射流參數關系式：

(19)

由于頂部起爆的線型聚能切割器所產生的射流沒有水平速度，不會造成能量損失，切割能力會高于端部起爆，所以僅需使用式(19)，按與端部起爆類似的設計流程進行計算校核即可。唯一應注意的是，頂部起爆時的炸高H變化較大。按圖7中的三角關系，可得：

(20)

式(20)的炸高值較端部起爆的式(14)增大，正切中增加了θ/2。按常用的爆炸切割器參數θ=20°，φ=45°，可求出H/h=1.01，比端部起爆的0.707增大43%。所以按照端部起爆設計的炸藥，從頂部起爆時，會有部分聚能罩失去作用。

2.2 切割器沿頂部高速起爆

聚能切割器沿頂部高速起爆是指沿切割器長度方向在頂部布置高速藥條進行起爆，這種起爆方法可以由高速敏感藥條帶動鈍感主裝炸藥穩定爆轟，保證爆炸切割效果。通常頂部敏感起爆藥條的爆速D要高于主裝炸藥爆速vd，其聚能切割器的立體透視關系如圖9所示。沿頂部高速起爆的切割器的碰撞運動與普通切割器的圖1差別很小，只是由于起爆藥條的爆速D高于主裝藥爆速vd，使主裝炸藥中爆轟波面由原來的OA向后偏到OE面。

圖9 沿頂部高速起爆聚能切割器的立體透視Fig.9 Stereoscopic perspective of shaped charge cutter high-speed initiated along the top

根據圖9所示關系，爆轟波偏轉角度μ應為

cosμ=vd/D

(21)

主裝炸藥對聚能罩的動態彎折驅動角為θ，有：

vp=2vdsin (θ/2)

(22)

圖10 沿頂部高速起爆的聚能罩立體透視Fig.10 Stereoscopic perspective of shaped charge liner initiated along the top

為了更加清楚方便地觀察高速起爆的切割器碰撞關系，重新繪制了與圖9反向的立體透視圖10。由圖10可見，高爆速炸藥的D帶動爆速vd的主裝藥以夾角μ落后于OA面，沿OE線被爆轟產物壓彎折，彎折角是θ，顯然下彎速度在與OE線為法線的平面內，將速度在此平面內分解，分別得出垂直與OE線的兩個分速度vdsinθ和vd(1-cosθ),vdsinθ在O′B′E面內。進一步將vd(1-cosθ)分解為O′E向和EA向速度。O′E向速度在O′B′E面內，為vd(1-cosθ)sinμ;EA向的速度vd(1-cosθ)cosμ與爆速反向流動。用速度比可以確定EB′的方向角度δ、速度值vE和炸高等，如下：

(23)

H/h=tg (φ+δ)sinφ

(24)

O′B′/h=cosδ/cos (φ+δ)

(25)

vE/vd=sinθ/cosδ

EB′/h=sinφ/cos (φ+δ)

還可用上面求出EB′長度，除以該方向上的速度vE作為聚能罩閉合的時間量tE，則有:

(26)

下面求取碰撞棱的角度β，也就要先求出圖2b中的GB段長度。聚能罩邊緣運動如圖9中的AEB過程，tE只是EB段的時間量，須補上AE段的長度(h·tgμ)。另外還要注意，聚能罩的水平運動速度需要在D上扣除圖10中EA向的速度，即x軸反方向的速度vd(1-cosθ)cosμ。則可得：

GB=h·tgμ+[D-vd(1-cosθ)cosμ]tE

用tgβ=OB′/GB，將式(25)和上式相除，并將式(22)代入，可得：

(27)

再利用圖2b中OK=OF=AEB=D·tE+h·tgμ和三角關系式h/OK=tg(α-β)與h/OF=tg(ψ-α)，可得：

(28)

求得射流角α和杵體角ψ度后，可利用式(21)和如下推廣的Taylor公式，以及碰撞過程的能量守恒關系：

整理后，得：

(29)

至此，已經全部求出沿頂部高速起爆的聚能射流參數。由于解析關系非常復雜，不再像1.1節一樣進行解析公式的最終推導，對于聚能射流參數可用α、β、ψ作為中間量進行計算。也可以簡單地由理論炸高式(24)分析可見，較一端起爆的式(14)多出了δ影響高度，而δ受式(22)控制，與θ/2和μ有關，并且δ<θ/2。所以沿頂部高速起爆炸高介于端部起爆和頂部同時起爆之間，也說明其射流向下的切割能力分量也是介于兩者之間。事實上本節公式是上述各種起爆情況的通用公式，μ=/2時為端部起爆，μ=0時為頂部同時起爆。由利用以上公式計算的各種起爆方式下的切割器射流參數(見表1)可見，沿頂部高速起爆D/vd=1時，所獲得的參數與一端起爆的完全相同；采用D/vd=100的高速起爆，計算結果與頂部同步起爆計算結果也一致。

表1 各種起爆方式下聚能切割器的射流參數

另外從Ejy來看，從一端起爆到高速起爆，一直至頂部同步起爆的Ejy是上升的，提高量13%～18%; 這說明切割能力有所提升，但提升幅度有限。由vf可見，如果使用爆速vd為6.0 km/s，則vf在1.3～1.9 km/s；若爆速vd為4.0 km/s，則vf在0.88～1.3 km/s；對于強度較高的聚能罩材料，vd為4.0 km/s的低爆速已經不太適用。再則，頂部起爆的vf比端部起爆的小，所以即便使用頂部高速起爆，反而可能使聚能切割能力下降。所以按上述方法，一般的工業炸藥用于切割器很難有較好的聚能切割效果。為此，2.3節將討論如何使用工業炸藥進行聚能切割的問題。

2.3切割器外表面高速起爆與爆轟驅動效率

1)切割器外表面高速起爆的解法。外表面高速起爆與端部起爆線型聚能切割理論幾乎完全一樣，如圖11所示，只是低爆速(vd)炸藥被表面高爆速(D)炸藥帶動以斜爆轟波驅動聚能罩，只要用低爆速炸藥的vp反求高速時的θD角，將其代入1.1節推導出的所有端部起爆公式，以θD和D替代θ與vd即可求解。θD的求解過程如下：

(30)

上式中μ如圖11中所示(vd=Dcosμ)。

圖11 沿上表面高速起爆的炸藥驅動飛板運動Fig.11 Plate flyer driven by the explosive high-speed initiated along upper surface

設炸藥爆速仍為上節的vd=4.0 km/s，聚能罩的vp=1.39 km/s，φ取45°,θ≈20°, 計算以D=6.0 km/s高爆速炸藥起爆(θD=13.3°), 計算結果如表2所示。由表中數據可見，理論上頂部高速起爆切割能量最高，但由于碰撞流速vf不到1.0 km/s, 對普通鋼聚能罩流速剛達到強度限，形成的射流必然很弱；對于退火純銅N≈20，形成射流尚可。常規端部起爆和表面高速起爆時，vf均可以使普通鋼聚能罩的N達到17～18, 實現切割。表面高速起爆的切割能量、射流速度、碰撞速度各項指標均比一端起爆略高，但提高的幅值有限，僅在3.5%～5%。

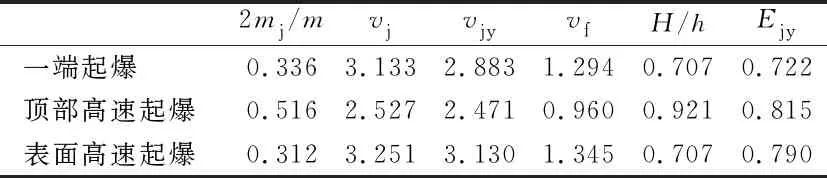
表2 各種起爆方式聚能切割參數對比

2)炸藥爆轟方式對飛片的加速能力。從上述計算看，似乎各種起爆方式對聚能切割的改變并不大，但事實并非如此，這就要從切割器的設計和炸藥驅動過程上考慮。通常為了使聚能罩達到高速度，切割器設計裝藥量很大，當采用工業炸藥時更是如此。而切割器聚能罩的最大飛行距離常常被設計在一到二倍藥厚之間，聚能罩的罩頂部有很大一部分的vp處于加速階段，沒有達到最終速度。罩頂這部分射流流速較低，會影響后續高速射流的前進，使射流縮短達不到h值(見圖12)。尤其是對于加速能力和爆速都不足的工業炸藥，往往是想通過增大聚能罩頂角φ來提高其加速距離，而頂角增加又會使碰撞流速vf下降到強度限以下，限制射流的產生，形成一對“矛盾”。

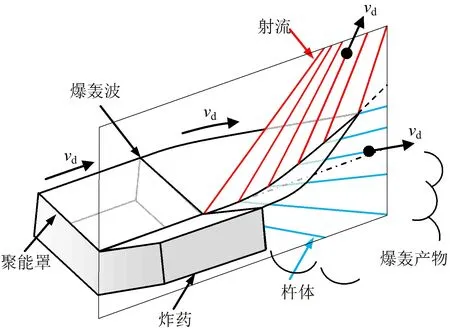
圖12 實際聚能切割器運動的圖像Fig.12 Diagram of actual shaped charge cutter movement

實際上，通過改變炸藥的起爆方式，完全可以縮短聚能炸藥的加速過程[8-9,29]。向一端起爆的滑移爆轟情況，施加在聚能罩上的最大壓力為炸藥爆壓，即：

(31)

式中：ρ0為炸藥密度；k為炸藥多方指數，k=1.6～3.5。

當炸藥逆向起爆或等容爆轟時，聚能罩飛片上的最大壓力pv可以由炸藥多方狀態方程和熟悉的爆轟CJ態密度ρc j=ρ0k/(k+1)，得：

(32)

上式取k=1.4～3.5計算，pv=(0.41～0.47)pcj。注意到飛片加速度與壓力成正比，顯然可知，滑移爆轟的加速能力要比等容爆轟高得多。

當飛片正向起爆時，就如同上述討論的表面高速起爆的爆速為無限大時，由于爆轟波會在飛片上反射而提高壓力，所以加速能力應該最高，爆轟波的固壁反射如圖13所示。

圖13 爆轟波的固壁反射Fig.13 Detonation wave reflected at rigid wall

爆轟波的固壁反射中，入射波后方為爆轟狀態，爆壓如式(31)，波后密度ρcj和速度ucj為

(33)

而反射的沖擊波陣面關系為

其中F下標代表反射波參數。在前面兩式中消去DF后，并通過整理，可有如下形式：

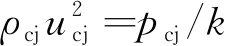
其解為

由于p>pcj, 上式中正解合理。固此，得到爆轟波在固壁上的反射壓力關系：

(34)

式(34)在k=1.4～3.5之間時, 計算反射壓力是爆壓的2.37～2.52倍。這比滑移爆轟高很多，所以加速能力很強。實際上，這不僅是正向起爆驅動飛片聚能的原理，也是爆轟波碰撞聚能[30]的原理所在。

由正向起爆驅動飛片的Aziz解[31]，等容爆轟驅動的Tan-Sun解[32]，滑移爆轟的二維特征線數值解[33]計算得出的飛板加速過程的對比如圖14所示。圖中Δ是以炸藥厚度為單位的無量綱飛行距離；R是單位面積炸藥量與飛片質量的比值。圖中為R=1，k=3的情況，可見各種爆轟方式的加速過程相差很大。以加速的終速的80%來看，等容爆轟Δ=0.18，滑移爆轟Δ=0.15，正向起爆的Δ=0.09，正向起爆的加速距離最短。而當切割器表面高速起爆時，在聚能罩上的斜爆轟波反射所產生的壓力與正反射非常接近，所以對切割器表面實施高速起爆，同樣可以縮短聚能罩加速距離，也就提高了罩頂部的利用率。

圖14 不同引爆方式的飛板運動對比Fig.14 Comparison of flyer motion driven by various detonation

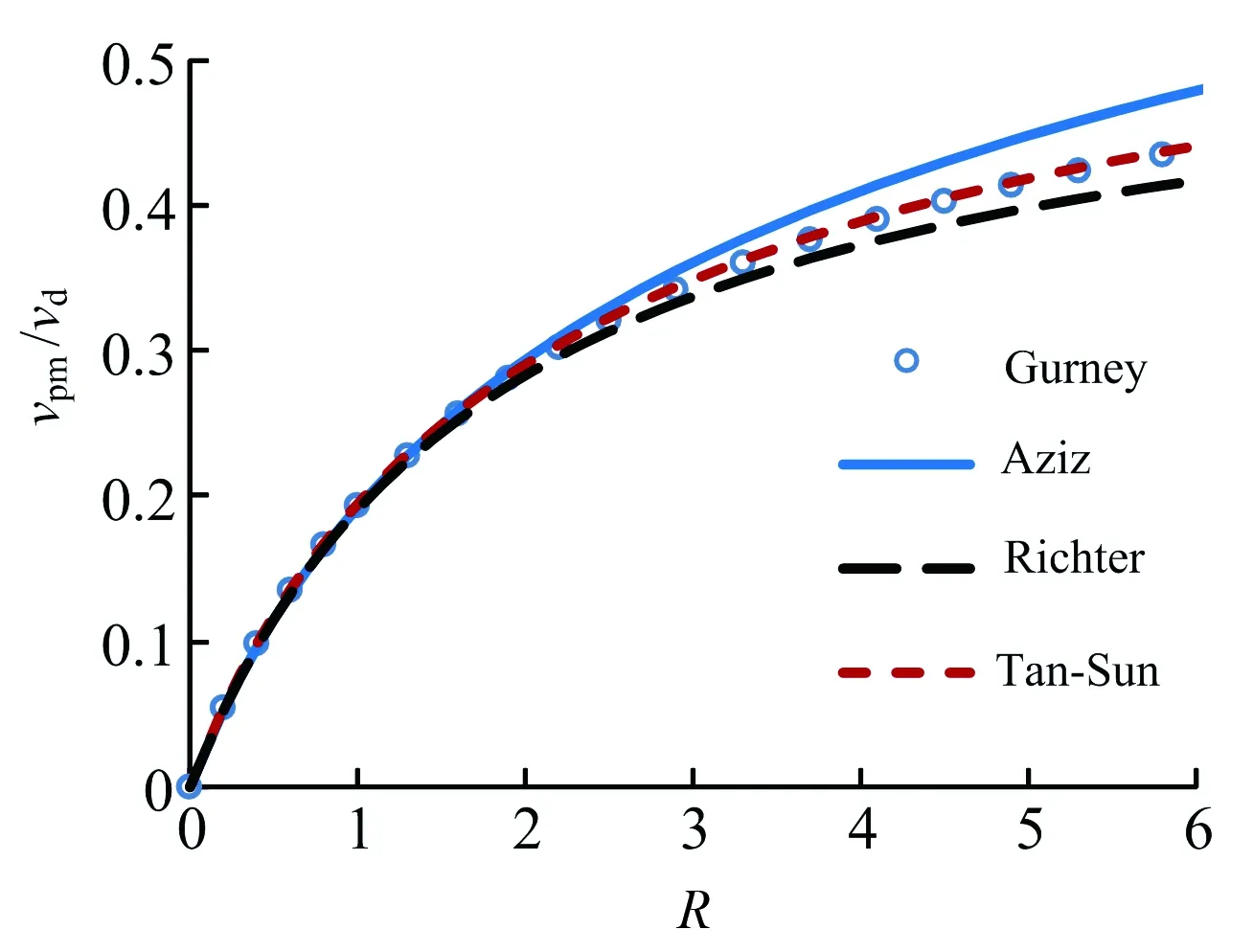
圖15 不同引爆方式的飛板終速對比Fig.15 Comparison of ultimate velocities of flyer driven by various detonation

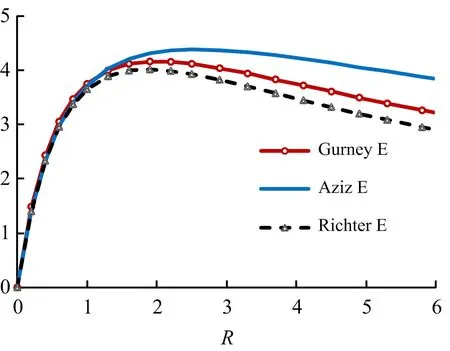
圖16 不同引爆方式的飛板極限動能對比Fig.16 Comparison of ultimate kinetic energies of flyer driven by various detonation

4)聚能切割器的雙線性高速起爆。前面討論了外表面高速起爆對聚能切割器切割能力的提高，但要實現切割器的整個外表面高速起爆并不容易，而且制造成本會很高。為此，作者提出了一種雙線性高速起爆的方案(見圖17)。在工業炸藥切割器的上部兩角處布置高速起爆藥條，如工業導爆索。以兩條高速線起爆，在主裝炸藥中形成錐形爆轟波，并在圖17橫截面中使爆轟波由聚能罩頂向下角逐漸碰撞，實現準外表面高速起爆。這種設計曾經用來切割鋼板，也用于邊坡預裂爆破。

圖17 雙線性引爆的工業炸藥聚能切割器Fig.17 Industrial explosive shaped charge cutter detonated with bi-lines

3 結語

本文從線型聚能切割器的三維流體模型出發，對端部起爆、頂部同步起爆、頂部高速起爆和外表高速起爆問題均給出了理論解法。并利用這些理論解，分析得到了切割器的切割深度、切割器設計炸高、聚能罩最佳頂角、聚能罩材料、裝藥量的計算公式和各種起爆方式的特點。這些理論已經成功用于各種型號線型聚能切割器的設計，如：拆除水下沉船和混凝土結構的爆炸切割器[34]，一次爆炸切斷近海油井的超大型切割器[10-11]，雙線性起爆的工業炸藥切割器[8-9]，以及石材爆破切割、炮孔內爆破切割等。理論和實踐表明，對于線型聚能切割器，完全可以采用上述理論方法結合實際經驗進行設計，設計流程如下：

首先，按破甲理論選定炸藥與聚能罩材料，將切割器的裝藥量選擇在R=1～3之間，以保證飛片吸收爆炸能量最優。然后用飛板拋擲公式或程序計算聚能罩彎折角θ(通常在10°～25°)。再用式(16)計算聚能罩的最佳頂角，并在附近選取φ值。接著對于所需起爆特點的切割器，采用其射流參數公式校核計算流體碰撞速度vf，使N值大于10，最好接近或高于20，以保證射流能克服聚能罩材料強度；同時校核vf小于聚能罩材料聲速。校核射流速度vj與靶板強度關系(見一般穿甲力學)，以保證射流速度足以克服靶板強度。計算確定理論切割深度Lt，以便實驗驗證。確定理論炸高H，并根據切割器形狀預估出正負浮動方向，以便實驗驗證。

端部起爆的聚能切割器由于必然要向爆轟方向分配部分射流能量，所以用于切割的能量會低于頂部高速起爆和頂部同步起爆。但頂部起爆的切割器其射流質量增加，射流速度vj與碰撞流速vf會降低，所以要注意校核射流形成與破甲的強度限；另外，頂部起爆的方式會使炸高增加，也應注意調整設計。表面高速起爆和雙線性起爆會縮短聚能罩的加速距離，提高罩頂部的利用率；實際上也能減少切割器邊部側向稀疏波的減壓；所以有提高聚能切割效果的作用。

本文作為線型聚能切割器設計基本理論，還只是對等藥量的切割器進行計算分析，對于變截面裝藥切割器，尚須根據實際經驗進行設計調整與實驗驗證。相信隨著計算技術的發展，復雜的三維線型聚能切割器設計理論會更加完善、成熟。