黃河河口入海流路的穩定類型和改道閾值體系

王開榮 杜小康 韓沙沙

摘 要：對黃河河口入海流路的穩定類型進行分類整理和概括總結，簡要回顧其人工改道標準閾值的演化和確定過程，初步構建入海流路實施改道的閾值體系，利用實測資料對典型流量級改道水位閾值、河長閾值、海域容沙閾值及其河口容許累計來沙量閾值進行了論證分析和計算。結果表明：現狀流量為3 000 m3/s的改道水位閾值為10.58 m，河長閾值約為89 km，海域容沙閾值約為72.19億m3，相應的利津站累計來沙量閾值約為120.65億t。

關鍵詞：河口;流路;穩定類型;閾值體系;黃河

Abstract：This paper classified， sorted and summarized the stability types of the Yellow River estuarine channel into the sea and briefly reviewed the evolution and determination process of the standard threshold of artificial avulsion. In addition， the threshold system for the implementation of the flow path avulsion into the sea was initially constructed. The threshold value of water level， river length， sea area sediment capacity and the threshold value of allowable cumulative sediment volume in estuary were analyzed and calculated by the measured data. The results show that the threshold of current water level is 10.58 m when the current flow reaches 3 000 m3/s， the threshold of river length is 89 km， the threshold of sea area sediment capacity is 7.219 billion m3 and the corresponding threshold of cumulative sediment inflow at Lijin Station is about 12.065 billion tons.

Key words： estuary; channel; stability types; threshold system; Yellow River

黃河河口入海流路的穩定問題一直是眾多學者所關注的重要課題，其治理實踐有特定的涵義[1]。眾所周知，“淤積、延伸、擺動、改道”是黃河河口在一定水沙條件下的自然規律。這一自然規律是黃河河口入海流路難以在平面區域位置保持穩定的具體表現，其中蘊含著不同類型的穩定問題，亟待給予明確;同時，現有的穩定改道閾值單純用水位特征值作為標準，有一定的局限性，并給人工有計劃改道的具體實施帶來諸多困擾[2] 。因此，如何在西河口（二）站流量為10 000 m3/s的水位達到12 m（大沽高程）這一改道水位閾值的基礎上，進一步補充和提出其他相關閾值指標，進而形成相對完善的黃河河口入海流路穩定閾值體系，也同樣值得研究。

1 河口流路的穩定類型和閾值指標

黃河河口地處陸、海相動力綜合作用的區域，其演變過程十分劇烈和復雜，既具有沖積性河流演變的基本特征，又受海洋動力因素的顯著影響。從實踐角度而言，黃河河口及其三角洲的演變過程盡管沒有絕對的平衡和穩定，卻蘊含著穩定平衡的形成機制和相應的臨界閾值。從現有的諸多研究成果來看，按照研究對象的不同和研究方向的差異，黃河河口的穩定可區分為6種不同的穩定類型，總結分析如下。

1.1 河道沖淤平衡型穩定

該型穩定主要是基于河床在縱向、橫向上抵御變化（形）的能力而提出的，本質上是判斷河床（槽）是否發生沖淤平衡穩定，主要考慮河道水流的挾沙能力及其河床邊界組成（主要是粒徑），落腳于河床[3]。竇國仁先生曾就此提出如下判別指標和控制閾值[4]：

當穩定系數接近于1.024時，即Ky≈1.024 時，河床穩定，不發生變形情況;Ky<<1.024時，發生沖刷;Ky>>1.024時，發生淤積。

這里需要指出的是：所謂沖積河流的穩定性指標，就是用來表明這種局部的、暫時的相對變異幅度，而不是用來闡明一條河流是否正處在平衡狀態[5]。

1.2 自然出汊型穩定

該型穩定是指入海行水河槽自身邊界條件不能滿足泄洪排沙要求，從而導致水流另尋其他捷徑入海的一種結果，落腳于局部河段，尤其是口門附近的尾閭河段，屬于自然演變（人工改汊除外）的范疇[6]。Jerolmack等[7]研究提出的出汊評判指標包括無量綱灘槽差SE、橫比降優勢參數K等[8]，計算公式如下：

1.3 河口沙嘴發育極限型穩定

該型穩定的基本涵義是：在河口沙嘴顯著凸出海岸線并進入濱海深水區時，將難以再向海延伸，從而促使河口沙嘴進入下一個演變周期。劉寶銀等[9]依據平行四邊形法則，建立了符合表達黃河口沙嘴延伸和發育的模型，見式（4），并就此指出當沙嘴發育指數趨近于0時，現行流路上的河口沙嘴將難以再向海延伸。

式中：Ω為黃河口沙嘴延伸和發育指數;L1為沙嘴根部長度;L2為沙嘴主軸長度;ω為沙嘴主軸與河口漲潮流向的夾角;t為河道主槽行水周期;e-it為河道主槽行水周期指數;Si為任一年的造陸面積;α為浪向與正北方向夾角;θ1為沙嘴主軸與正北方向夾角。

1.4 海岸線延伸蝕退平衡型穩定

該型穩定是指在一定來水來沙條件下，河口三角洲岸線的某一區域在某一時段內，因淤積和侵蝕數量相當而導致三角洲總體造陸面積不再增長的一種狀態;其所涉及的區域可以是整個黃河三角洲岸線，也可以是處于行河狀態的流路所涉及的海岸線區域[10-14]。張治昊等[15]利用1977—2002年實測資料，通過多元回歸分析建立了如下黃河口海岸造陸水沙臨界綜合關系式：

1.5 三角洲沖積扇生長極限型穩定

提出該型穩定的主要依據在于：由河流入海泥沙在河口及其鄰近區域不斷堆積而逐漸形成的河口三角洲存在地貌學意義的生長極限[16-18]。曹銀真[19]提出：三角洲沖積扇發育是不斷循環的過程，每一循環過程形成的幾何形態基本一致，即沖積扇的縱軸a（即平行于河道的最大長度）、橫軸b（即垂直于河道的最大長度）、沖積扇的圓心角之間總保持著一定的比例關系，都有一定的臨界幾何形態;統計結果表明，現代河口三角洲只要其形態指標a/b值達1.2左右時，河道便發生決口改道（突變），另循比降大、流程短的地帶重新塑造新三角洲。

1.6 人工改道標準型穩定

該型穩定屬于人工干預下的控制穩定。眾所周知：1855年至20世紀70年代，黃河入海流路的改道多屬于自然、隨機地發生，或者是在極其被動的情況下實施。而在目前，入海流路的改道則完全受制于人類活動的干預和影響，并且是有規劃、有計劃地予以實施。當前，基于現狀條件下現行清水溝流路所能承受的防洪壓力乃至黃河下游的堤防標準情況，其河口入海流路的改道閾值標準是西河口（二）站水位在流量為10 000 m3/s時達到12 m。

西河口（二）站12 m水位改道標準是當前黃河河口綜合治理進程中一項至關重要的控制指標。其存在的重大實踐意義在于：若出現流量為10 000 m3/s的情況，其西河口水位不能超過12 m。若水位超過12 m，為確保防洪安全，必須對其上游相當長的一段堤防進行重新加高加固，但加高黃河堤防絕非治河上策，堤防越高，風險和影響范圍就越大[20]。

需要特別指出的是：在上述6個不同的穩定類型中，人工改道標準型穩定在河口治理實踐中具有特殊的重要地位。鑒于此，本文圍繞這一穩定類型的閾值演化過程和輔助閾值體系作如下進一步分析。

2 流路人工改道標準閾值的演化和確定

縱觀1855年以來黃河河口的演變及其治理進程，其流路改道標準閾值的演化和確定經歷了如下3個階段。

第一階段：1855—1953年自然閾值階段。河口基本屬于自然演變狀態，人工干預強度極弱，其穩定閾值沒有明確的概念和數值大小。

第二階段：1953—1992年10 m（大沽高程）改道標準階段。該階段是流路穩定判別指標由自然狀態下的穩定閾值向人工控制改道標準轉變的階段。1946年開啟人民治黃歷程，1953年前，黃河由甜水溝、宋春榮溝、神仙溝分流入海。長期分流入海造成上游河道壅水淤積，為改善防洪條件，變分流入海為獨流入海，于1953年7月實施了并汊改造。此時的改道一般是相機臨時決定的，并無統一、嚴格的改道標準閾值。1964年因凌汛問題改道刁口河流路后，適逢黃河第三次加高加固黃河大堤（1969—1973年），其下游堤防防御標準為花園口站22 000 m3/s洪水。基于此，20世紀70年代初，根據當時黃河河口堤防的工程標準，把洪峰流量為10 000 m3/s時羅家屋子大體相應的水位達到10 m（大沽高程）作為改道控制水位。

第三階段：1992年至今12 m（大沽高程）改道標準階段。20世紀80年代以來，尤其是1983年東營市的建制成立，河口三角洲地區社會經濟的持續發展，以及勝利油田的大規模開發，對黃河河口入海流路穩定的要求愈發迫切。基于河口地區防洪工程體系的建設現狀，1992年原國家計委正式批復《黃河入海流路規劃報告》，明確了“當西河口（二）水位站水位達12 m時，再根據當時河道狀況及油田開發需要決定改走北汊1或抬高西河口水位繼續走現行河道”。最新的《黃河河口綜合治理規劃報告》即采用了此改道標準。

河口堤防是防御洪水泛濫、保護河口三角洲地區居民和工農業生產的主要工程舉措。現狀條件下的黃河河口河道堤防設防標準與黃河下游的堤防有所不同，其包含了兩層含義，其一是能保障10 000 m3/s流量過程的行洪安全，其二是西河口水位在流量為10 000 m3/s時達到12 m應實施人工有計劃改道。

目前，黃河河口河道堤防（指臨黃堤防）全長約75.9 km，其中左岸堤防全長44.4 km，包括北大堤（四段—三十公里險工）長度30 km、北大堤順六號路延長段（三十公里險工以下至孤東圍堤三號險工）長度14.4 km。堤頂高程自上而下為14.88～7.15 m（黃海高程，下同），西河口水位（二）站對應的左岸堤頂高程約為13.50 m（清1斷面左岸，換算大沽高程為14.98 m）。左岸堤防全長31.5 km，包括臨黃大堤（漁洼—二十一戶）長度3.7 km、防洪堤（二十一戶以下至防潮壩）長度27.8 km，其堤頂高程自上而下為14.30～8.60 m，西河口水位（二）站對應的右岸堤頂高程約為13.35 m（清1斷面右岸，換算大沽高程為14.83 m）。

3 流路改道標準的輔助閾值指標

3.1 輔助閾值指標的構成

目前流路的改道與否是以水位作為控制標準的，由此帶來了如下問題：第一，水位并非表征流路末期演變狀態的唯一特征值，水面比降、尾閭長度、相應濱海區域容沙能力乃至生產實踐的需求等，都在一定程度上影響和決定著入海流路是否要進入改道程序。第二，將水位作為改道的唯一控制標準，需要準確把握河口河段的水位變化，但就黃河河口的基本演變特征而言，預測短時期內的水位變化難度極大。河口河段水位變化十分劇烈，以西河口流量為3 000 m3/s時的水位變化為例，個別年份水位升高值可達0.58 m（1993年），尤其需要指出的是，河口地區的凌汛、風暴潮都有可能導致水位暴漲[21]。1979年1月25日，利津站凌峰流量為1 130 m3/s的水位一度達到了14.76 m，較1978年11月中旬、1979年7月中旬同流量水位分別升高了2.37 m和2.72 m，該數值也超過了1958年流量為10 400 m3/s時的水位13.76 m。顯然，將單一水位閾值作為改道決策依據存在一定的局限性，應參考其他相關閾值并據此形成相對完善的改道輔助閾值體系，才會使得改道的決策更為科學和合理。

基于上述原因，圍繞西河口12 m水位的改道閾值問題，衍生了其他相關的輔助閾值指標，主要包括典型流量級的改道水位閾值、河長閾值、濱海區域容沙體積閾值，其中海域容沙閾值亦可轉化為河口所容許的累計來沙量，見圖1。

3.2 典型流量級的改道水位閾值

自20世紀80年代中期以來，黃河口地區來水來沙量急劇銳減，洪峰流量亦大幅度削減。1986—2016年最大日均流量僅為5 220 m3/s（1988年），多年平均最大日平均流量為2 713 m3/s;31 a中只有9 a最大日平均流量超過3 000 m3/s;而且，在目前黃河多水庫聯合運用和黃河下游滯洪區運用的情況下，河口河段10 000 m3/s洪水出現的概率為千年一遇。鑒于此，十分有必要基于流量為10 000 m3/s時12 m水位的改道標準，分析和計算典型流量級所對應的改道水位閾值。

考慮到在傳統的水文分析計算中，流量為3 000 m3/s的水位已被廣泛采用這一現實，故選用3 000 m3/s作為典型流量級為宜。之所以把流量為3 000 m3/s的水位作為關系指標，主要是基于在進入河口河段的洪峰過程中3 000 m3/s流量出現的頻次最高。統計結果表明：在小浪底水庫運用期的2002—2016年15 a中，各年度最大日均流量的平均值為3 164 m3/s，其中有9 a最大日均流量超過了3 000 m3/s，而超過4 000 m3/s流量過程的年份僅有1 a，因此選用3 000 m3/s對應水位作為關系指標既符合未來的水沙情勢，又可以利用實測資料獲取客觀和真實的數據。

將西河口流量為10 000 m3/s時12 m的改道水位轉換為流量為3 000 m3/s時的相應水位，并沒有改變現行入海流路的改道標準，同時，轉換后的水位指標更切合實際，更容易科學把握。事實上，在開展黃河口入海流路規劃和綜合治理規劃時，其水位指標的轉換已經得到了不同程度的運用，并大致給出了其水位差在1.27～1.87 m之間變化[22-24]。

根據2017年實測資料，西河口水位（二）站附近所對應的斷面（清1斷面）主槽寬度和河床平均高程分別為629.0 m和4.35 m，灘地寬度和灘地平均高程分別為691.4 m和7.53 m，設定主槽綜合曼寧糙率系數為0.0125，灘地糙率分別選用0.02、0.03、0.04和0.05，主槽比降為0.007 5%，灘地比降為1.420/1 000，依據曼寧公式則可得到演算成果（見表1）。由此可見：現狀條件下流量為3 000 m3/s與10 000 m3/s對應水位的差值在0.98～1.57 m之間。在不考慮河床形態、海平面上升等其他相關因素的情況下，若灘地糙率取值為0.04，其現狀流量為3 000 m3/s的改道水位閾值為10.58 m。

3.3 河長閾值

河口流路延伸長度的變化既是表征河口演變的主要特征指標，也是影響河流侵蝕基準面變化的主要因子和制約河口河段水位變化的核心因子。因此，河口入海流路延伸長度的變化一直是開展河口演變規律及其綜合治理研究的核心內容。圍繞流路的河長閾值（西河口以下）問題，相關研究得出和采用的數值介于76.9～83.0 km之間[23-25]。

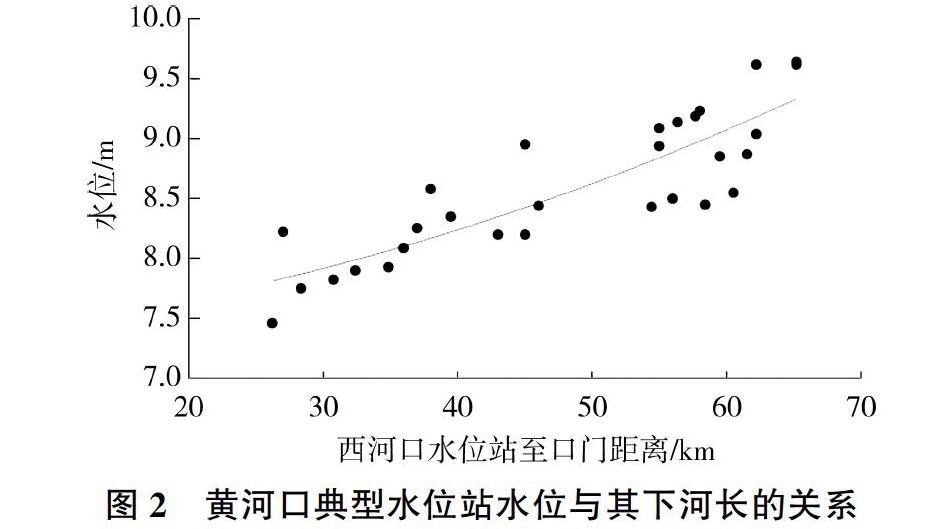
流路河長的變化對于河口尾閭河段的水位升降變化和發展趨勢具有控制性的影響[26]。利用1965—2002年的部分實測資料，并將羅家屋子水位轉換為西河口（二）站水位，可建立其水位與河長間的相關關系（見圖2），并得出如下關系式：

依據式（6），并取西河口流量為10 000 m3/s與3 000 m3/s對應水位差1.42 m（灘地糙率取值0.04），在不考慮海平面上升等因素的情況下，可得出河長閾值約為89 km。

3.4 海域容沙閾值

海域容沙閾值是指基于現狀海域地形條件，在未來清水溝流路行河達到某種特定狀態時，其行河所涉及的海域能夠容納的泥沙數量，此與陳雄波等[27]提出的“流路輸沙容量”概念并無本質的區別。1992年原國家計委正式批復的《黃河入海流路規劃報告》，曾就不同海域的容沙體積（庫容）進行過計算[22]。

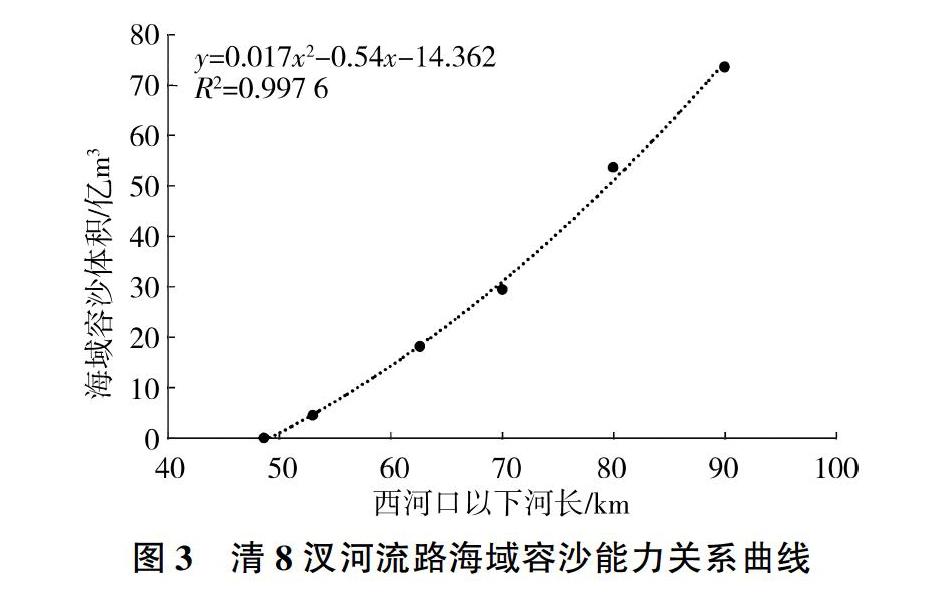
筆者利用1996年的實測濱海地形資料，并以三角洲沖積扇生長極限型穩定所得出的幾何形態閾值為依據[19]，在預測概化清8汊河未來沙嘴形態的基礎上，選擇沙嘴頂部寬度介于3～9 km之間，從而進一步明確了流路河長與海域容沙能力的相關關系（見圖3），得出了在河長達到89 km的情況下，其海域容沙閾值約為72.19億m3。

需要說明的是：海域容沙閾值也可以用利津站所容許的累計來沙量所代替。眾所周知，進入河口的泥沙輸移分配的區域不外乎三個，分別是河道內、濱海區和外海，其中沉淤在河道內、濱海區兩個區域的泥沙均會參與造陸并形成流路河長的延伸。根據以往研究成果，在多年平均情況下河道內、濱海區沉淤的泥沙數量占利津來沙量的比例約為70%。據此可大體得出：當海域容沙能力達到閾值72.19億m3時，其利津站所容許的累計來沙量閾值為103.1億m3（考慮淤積物干密度介于陸上淤積物和濱海區淤積物干密度之間，取1.17 t/m3）[26，28]，則得出相應的利津站累計來沙量閾值約為120.65億t。

截至2018年，清8汊河累計來沙量為36.44億t，尚余84.21億t的容沙能力空間，若考慮未來河口年均入海沙量為3.0億t，則清8汊河的行河年限約為28 a。

4 結論及建議

目前，現行清水溝流路的改道水位標準是西河口水位在流量為10 000 m3/s時達到12 m（大沽高程），由此衍生的其他相關輔助閾值指標包括：①典型流量級的改道水位閾值，若灘地糙率取值為0.04，其現狀流量為3 000 m3/s的改道水位閾值為10.58 m;②河長閾值，基于水位與河長間的相關關系，可得出河長閾值約為89 km;③海域容沙閾值，通過明確流路河長與海域容沙能力的相關關系，得出在河長閾值達到89 km的情況下，其海域容沙閾值約為72.19億m3;④利津站累計來沙量閾值，根據進入河口地區的泥沙輸移分配比例，得出相應的利津站累計來沙量閾值約為120.65億t。目前的清8汊河流路尚余84.21億t的容沙能力空間，若考慮未來河口年均入海沙量為3.0億t，則清8汊河的行河年限約為28 a。

按照研究對象的不同和研究方向的差異，黃河河口的穩定可分為6個種穩定類型，即河道沖淤平衡型穩定、自然出汊型穩定、河口沙嘴發育極限型穩定、海岸線延伸蝕退平衡型穩定、三角洲沖積扇生長極限型穩定、人工改道標準型穩定。鑒于人工改道標準型穩定在河口治理實踐中具有特殊地位，故對其改道閾值體系進行了先期研究。鑒于黃河河口入海流路演變的復雜性以及對流路實施改道的高度敏感性，建議對其他5項穩定指標體系也展開閾值研究，并形成完整的河口入海流路閾值體系。

參考文獻：

[1] 王開榮，杜小康，鄭珊，等.黃河河口及其流路系統的構成和穩定內涵 [J].人民黃河，2018，40（8）：30-35，47.

[2] 王開榮，陳孝田，趙陽.黃河口現行尾閭流路改道標準及其評價[J].人民黃河，2009，31（5）：23-25.

[3] 陸倩，龔政，李歡，等.平原沖積河流及潮汐河口河相關系研究進展[J].人民長江，2013，44（21）：7-11.

[4] 竇國仁.平原沖積河流及潮汐河口的河床形態[J].水利學報，1964（2）：1-13.

[5] 錢寧.沖積河流穩定性指標的商榷[J].地理學報，1958，24（2）：128-144.

[6] 王愷忱.黃河口演變規律及其對下游河道的影響[C]//黃委會水科所.黃委會水科所科學研究論文集（第2集）.鄭州：河南科學技術出版社，1990：154-201.

[7] JEROLMACK D J， PAOLA C. Complexity in a Cellular Modelof River Avulsion[J]. Geomorphology， 2007， 91（3-4）：259-270.

[8] SLINGERLAND R， SMITH N D. Necessary Conditions for a Meandering-River Avulsion[J]. Geology， 1998， 26（5）：435.

[9] 劉寶銀，王巖峰，高俊國.近期黃河口沙嘴演變遙感信息的拓撲模型研究[J].海洋學報（中文版），2000，22（2）：41-47.

[10] 常軍，劉高煥，劉慶生.黃河口海岸線演變時空特征及其與黃河來水來沙關系[J].地理研究，2004，23（3）：339-346.

[11] 王開榮，茹玉英，陳孝田，等.黃河河口三角洲岸線動態平衡問題的探討[J].泥沙研究，2007，32（6）：66-70.

[12] 崔步禮，常學禮，陳雅琳，等.黃河水文特征對河口海岸變化的影響[J].自然資源學報，2006，21（6）：957-964.

[13] CUI B L， LI X Y. Coastline change of the Yellow River Estuary and Its Response to the Sediment and Runoff （1976-2005）[J]. Geomorphology， 2011， 127（1）： 32-40.

[14] WANG S J， MARWAN A H， XIE X P. Relationship Between Suspended Sediment Load， Channel Geometry and Land Area Increment in the Yellow River Delta[J]. Catena， 2006， 65（3）： 302-314.

[15] 張治昊，胡春宏.黃河口水沙過程變異及其對河口海岸造陸的影響[J].水科學進展，2007，18（3）：336-341.