點線嚙合齒輪動態接觸應力仿真分析與齒廓修形

武漢理工大學工程學院 武漢 430063

0 引言

點線嚙合齒輪既具有漸開線齒輪加工方便、可分性的優點，又同時囊括了圓弧齒輪承載能力高的優點，有較好的發展前景。點線嚙合齒輪由漸開線齒輪滾刀滾切而成，在嚙合過程中存在干涉現象[1]，主要有兩種：一種是過渡曲線干涉，一種是旋動曲線干涉。由此造成了齒輪嚙合過程中的沖擊噪聲，一般通過修形解決這一問題。而沖擊噪聲又分為小齒輪齒根與大齒輪齒頂剛進入嚙合時產生的嚙入沖擊，和小齒輪的齒頂提前與大齒輪的過渡曲線接觸而產生的接觸沖擊。

目前，點線嚙合齒輪傳動作為一種新型的齒輪傳動，其接觸問題分析尚不完善，計算上一般采用赫茲公式求取單對嚙合區C點附近接觸應力作為其最大接觸應力，試驗中一般采用經驗數值作為修形參數。因此，明確點線嚙合齒輪在嚙合接觸過程中主要發生的干涉和沖擊類型，產生的接觸應力大小及變化情況，驗證經驗數值修形的可靠性對完善點線嚙合齒輪研究理論體系具有重大意義。

1 點線嚙合齒輪三維建模

由于點線嚙合齒輪齒廓形狀的特殊性，使其無法像一般漸開線齒輪利用三維建模軟件內部某些插件直接生成模型。而為了得到精確的分析結果，則需要更高精度的三維模型。文中以點線嚙合齒輪的齒廓曲線方程為基礎，利用三次樣條曲線分段插值法擬合齒輪齒廓上的點，得到齒廓曲線，在SolidWorks中搭建三維模型。

1.1 點線嚙合齒輪齒廓曲線方程

點線嚙合齒輪的加工方式和漸開線齒輪一樣通常是滾齒機床加工，如圖1所示，根據齒條齒廓上所有點在動坐標系中的坐標，可以求出被加工齒輪齒廓上對應各點在靜坐標系中的坐標，即可求出點線嚙合齒輪的齒廓曲線方程[1]。

圖1 滾刀齒廓

點線嚙合齒輪的干涉主要發生在漸開線齒廓段，這一段由齒條刀具直線段b＇b＇包絡而成，如圖2所示，其上任意一點M＇的法線與M1軸交點N坐標為(x1，y1)。

圖2 滾切點線嚙合齒輪

將式(1)代入被加工齒輪齒廓普遍方程式(2)中，即可得到未修形齒輪齒廓方程

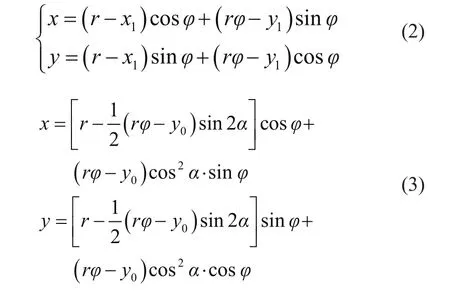
同樣地，對于修形齒廓，文中采用的二次漸開線修形是在刀具刀根處進行修改，如圖3虛線部分所示。當改變刀具壓力角α為α＇時，得到被加工齒輪修形高度ht，修形量Δt。將虛線段上任意一點的法線與Y1軸交點坐標設為Nt(xt，yt)，那么

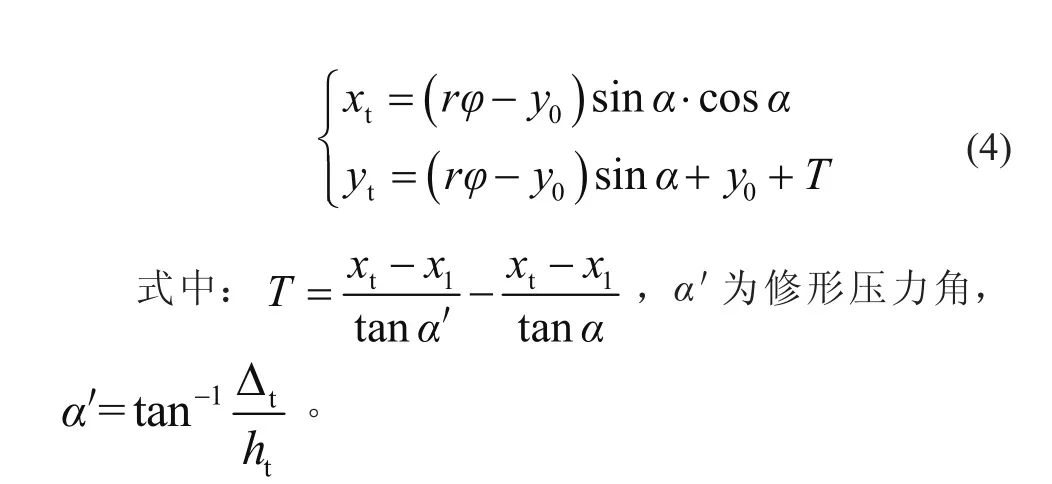
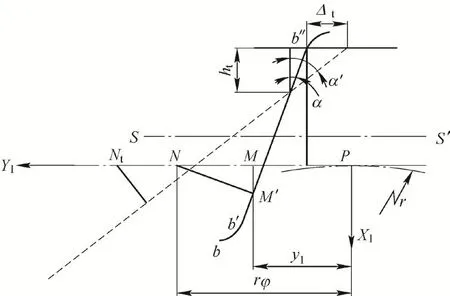
圖3 滾切點線嚙合齒輪修形示意

同樣地，將每一點坐標代入式(2)中，即可得到修形部分的齒輪齒廓方程

1.2 建立三維切齒模型

通過點線嚙合齒輪的齒廓曲線方程，可求得點線嚙合齒輪齒廓曲線上一系列的點集的集合[3]，再利用插值法三次樣條曲線來擬合這些離散點，得到刀具的參數方程，從而推導出點線嚙合齒輪的齒廓方程[4]。

文中針對DZLY180型硬齒面點線嚙合齒輪減速器高速級齒輪副進行研究，分別建立未修形和修形后兩組齒輪副模型，其主要幾何參數及修形參數如表1所示。以未修形齒輪副模型為例，根據齒廓曲線擬合點形成的大齒輪端面齒廓曲線如圖4所示。

圖4 未修形點線嚙合齒輪端面齒廓曲線

表1 高速級齒輪副主要幾何參數及修形參數

由于瞬態動力學計算量較大，為了節省有限元分析的計算時間，又兼顧計算精度，同時考慮到點線嚙合齒輪斜齒輪副的重合度，保留該齒前后各3對輪齒，將完整的齒輪副模型截取7對齒，作為切齒模型進行分析[5]。切齒模型如圖5所示。

圖5 點線嚙合齒輪切齒模型

2 Ansys Workbench瞬態動力學仿真

選用Ansys Workbench中的瞬態動力學模塊對以上點線嚙合齒輪切齒模型進行仿真分析，相較靜態分析計算量龐大，但優勢在于能夠看到輪齒在嚙合過程中接觸應力的動態變化情況。

文中研究的DZLY180型齒輪減速器中高速級齒輪副，大小齒輪所采用的材料是均為合金鋼，其主要材料屬性如表2所示。

表2 DZLY180型減速器齒輪材料屬性

相較于Ansys經典界面，Ansys Workbench可以自動劃分網格，不需要手動選擇網格單元類型。一般來說，六面體網格比四面體網格質量更高，得到的計算結果精度更高，且在同樣網格尺寸的情況下，六面體網格數量較少，可以縮短計算時間。因此，為了保證表面的單元質量，采用六面體主導的網格劃分方法[6]。該單元劃分方法在表面使用六面體單元，在內部也優先使用六面體單元，而當無法用六面體單元時，就用四面體單元填充。對主要參與嚙合的5對輪齒的接觸面再次進行局部網格細化，最終生成網格如圖6所示。

圖6 切齒模型網格劃分

轉速和扭矩載荷通過轉動副載荷實現，設置主動輪轉動副載荷為轉速，從動輪轉動副載荷為轉矩。根據DZLY180型減速器實際參數，主動輪小齒輪轉速1 000 r/min，從動輪大齒輪所受阻力矩2 176.04 N·m。

3 齒廓修形前后接觸分析對比

為方便表述，將完成嚙入到嚙出過程的1對輪齒作為主要觀測對象，記為N齒。分別對修形前、后兩組模型經上述方法進行仿真，得到N齒動態接觸應力變化云圖。為方便觀察，間隔均勻時間截取7張小齒輪上N齒應力云圖，如圖7所示。從左側看，小齒輪順時針旋轉。圖示自上而下為N齒從嚙入到嚙出過程中接觸應力的變化情況，左列為修形前齒輪，右列為修形后齒輪。將兩組齒輪最大接觸應力值隨時間變化圖線繪在一張表上，如圖8所示，方便清晰地對比修形前、后兩組齒輪副上接觸應力變化。圖7中每一幅應力云圖自上而下一一對應a～g時刻。

圖7 修形前（左）與修形后（右）N齒接觸應力

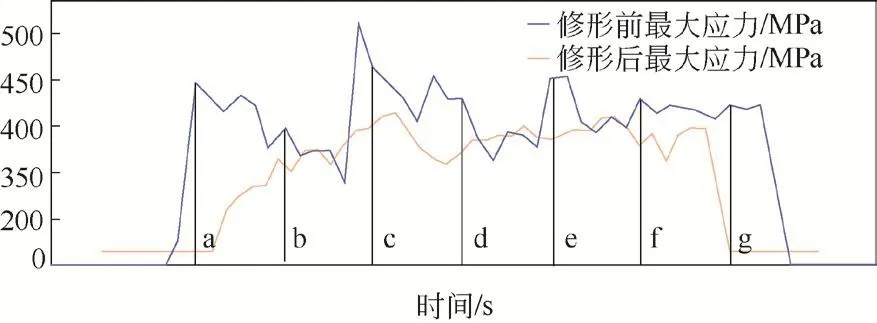
圖8 修形前后最大接觸應力隨時間變化情況

首先比較圖8中兩曲線波動情況，可以看到修形后最大接觸應力變化趨勢明顯減緩，同時，修形后總體接觸應力值也明顯降低。相應地，在圖7中相比左列修形前圖像，右列修形后的應力云圖顏色分布更均勻。說明文中采用的修形方案對這對齒輪嚙合的平穩情況有了較大改善。

其次，對比兩曲線發現，還未修形的齒輪有兩處接觸應力值突增，分別在a時刻和c時刻附近。下面分析這一現象產生的原因。

對于c時刻附近，在t= 6.472 6×10-3s時刻，最大接觸應力突然增大到峰值521.18 MPa。這是由于齒輪在嚙合過程中，一般是單齒嚙合與雙齒嚙合交替進行，在a時刻到c時刻之間，N齒的前一個齒還未退出嚙合，此時N齒與前一齒共同參與嚙合，為雙齒嚙合區；到c時刻，前一齒退出嚙合，由N齒單獨完成嚙合，故此時接觸應力達到峰值，一直到f時刻，為單齒嚙合區；f時刻后，后一齒加入嚙合，再次進入雙齒嚙合區；到g時刻過后，N齒退出嚙合。在齒輪實際傳動過程中，主動輪的基節與被動輪的基節大小不同，交替嚙合時易出現干涉現象，造成齒輪嚙入沖擊。

此時的應力云圖如圖9a所示，接觸的輪齒上產生了較大的應力集中，即圖中紅色區域。且由于該處應力與其余接觸部分應力差值過大，導致其余部分應力云圖難以顯示完整。對該應力集中位置進行端面切片（見圖9b），找到應力集中發生在小齒輪的齒根與大齒輪的齒頂接觸處，說明未修形的齒輪副在嚙入過程中，該處發生干涉，產生嚙入沖擊。

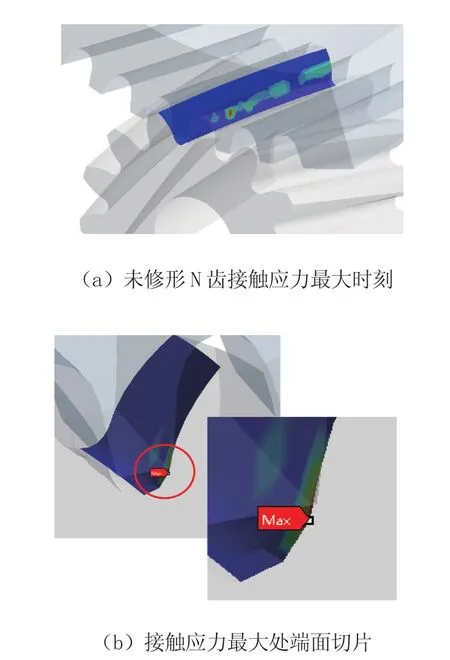
圖9 應力云圖

而在同一時刻，修形后齒輪上應力云圖如圖10a所示，不難看出接觸應力值過渡平緩，沒有產生明顯的應力集中現象。同樣在產生最大應力處切片，如圖10b所示，原本發生在未修形的小齒輪齒根與大齒輪齒頂接觸處的干涉現象已被消除。

圖10 應力云圖

對于a點時刻，修形前、后的最大接觸應力值相差甚遠，對應接觸應力分布分別如圖11a和圖12所示。在這一時刻，N齒剛剛開始進入嚙合，同時前一對齒還未退出嚙合，為雙齒嚙合區，理論上接觸應力應主要由前一對齒承擔。然而，未修形齒輪上出現了應力集中，其最大接觸應力遠超前一對齒。此時在大齒輪齒頂與小齒輪齒根接觸部位發生干涉，造成載荷突變，如圖11b所示。修形之后，載荷均勻分布在前一對齒上，小齒輪齒根的應力集中消除，接觸情況符合理論分析。

圖11 應力云圖

圖12 a時刻的修形后N齒

4 結論

通過查看一對齒在完整嚙合過程中接觸應力隨時間變化的情況，發現點線嚙合齒輪在嚙合過程中產生的沖擊主要是嚙入沖擊，主要發生在小齒輪齒根與大齒輪齒頂接觸時和大齒輪齒頂與小齒輪齒根接觸時兩處。經過二次漸開線修形以后，通過修形前后的結果對比，表明點線嚙合齒輪的應力集中情況以及嚙合的平穩性都有了很大改善，證明試驗中采用的修形方案有一定可行性，更精確的修形參數可進一步研究。