事件觸發機制下的充液航天器姿態控制

董新蕾，齊瑞云，*，盧山，王煥杰

（1.南京航空航天大學 自動化學院，南京211106；2.南京航空航天大學 先進飛行器導航、控制與健康管理工業和信息化部重點實驗室，南京211106；3.上海航天控制技術研究所，上海201109； 4.上海市空間智能控制技術重點實驗室，上海201109）

液體燃料以其經濟、可靠等優勢，在航天運載中得到了廣泛的應用［1］。而航天器執行的空間任務周期更長、要求更高，對液體燃料的需求量也就更多。部分充滿的液體燃料隨著航天器的機動而發生晃動，晃動的液體燃料一方面影響充液航天器的轉動慣量，另一方面對系統產生干擾力、力矩，導致航天器任務的執行失敗，甚至引發航天事故［2］。所以，對液體晃動的建模及對充液航天器控制器設計的研究，十分具有工程意義。

隨著對液體晃動影響的重視，對液體晃動建模方法的研究成果也頗多。其中，等效力學模型簡單、高效，相對于其他試驗、理論、數值仿真等研究方法，更有利于控制器的設計。現有等效力學模型中，研究較為成熟且被控制系統設計廣泛采用的主要有單擺模型，其將晃動的液體部分等效為質量、擺長固定的單擺，用擺角的變化描述液體的晃動行為，一旦液體晃動的幅度占充液腔體半徑的比例達到25%以上，呈現出大幅且非線性的特點，該等效模型則不再適用。此時，可用的等效力學模型主要有運動脈動球模型［3］、多級擺模型、質心面模型［4］等。其中，運動脈動球模型被用在Sloshsat FLEVO（Sloshsat Facility for Liquid Experimentation and Verification On-Orbit）衛星的控制方法研究中，不同工況下的試驗數據表明了該模型可準確地等效液體大幅晃動。

進行充液航天器的姿態控制器設計時，主要考慮轉動慣量的不確定性及外部環境的干擾等因素，所以控制系統應具有良好的自適應性與魯棒性［5］。其研究方法主要有：①滑模控制方法。其是在研究非線性系統時，經常被使用的控制方法，具有魯棒性強、設計與實現簡單的優點。文獻［6］針對欠驅動系統，就航天器和液體晃動的狀態量設計了分層滑模面，具有鎮定姿態和抑制液體燃料在貯箱內晃動的控制效果。文獻［7］在考慮液體大幅晃動和撓性附件振動的情況下，設計了線性滑模面，對姿態系統進行滑模控制，并結合自適應算法來提高控制精度，最終實現了對目標姿態的精確追蹤。文獻［8］將自適應思想與終端滑模控制2種方法結合在一起，在有限時間內實現了各狀態量的收斂，相比于一般漸近穩定的控制方法，該方法在收斂速度上更快、精度也更高。文獻［9］引入輸入整成型技術，在保證控制效果的同時，有效地抑制了變量的抖震。②模糊控制方法。文獻［10］基于局部線性模型的加權和建立了非線性T-S模糊模型，在此基礎上分別設計了并行分配補償（Parallel Distributed Compensation，PDC）控制方法和線性二次調節器（Linear Quadratic Regulator，LQR）控制方法，仿真表明，PDC控制方法在控制性能和魯棒性上效果更佳。③非線性反饋控制方法。文獻［11-12］分別考慮液體小幅、大幅晃動的情況，基于彈簧-質量塊模型和運動脈動球模型，使用基于Lyapunov函數的方法，進行反饋控制器的設計。文獻［13］考慮外部干擾的存在及部分未知的參數，設計了自適應算法與非線性反饋控制方法相結合的混合控制器，獲得了較好的姿態鎮定效果，液體的晃動行為也逐漸平穩。

與此同時，航天器的計算機資源有限，如果通信頻繁，不但會堵塞通信信道，也會對航天器的正常運行、使用壽命造成惡劣的影響［14］。傳統的控制方法每隔固定的時間就會對信號進行更新，但部分信號的更新是沒有必要的，這樣會造成通信的資源浪費。而事件觸發機制只有在滿足事先設定的事件時，才會對信號進行更新，其可以在保證控制效果的同時，顯著地降低通信頻率［15］，減輕通信負載。文獻［16］針對系統傳感器與控制器間狀態量的更新，提出了基于擾動理論的事件觸發機制，最終剛體航天器的姿態實現了指數型穩定。文獻［17］考慮航天器系統存在外部干擾力矩的情況，結合反步法與逆最優控制方法，并在控制器端引入決定控制信號更新的事件觸發機制，穩定性證明與仿真結果都表明該方法保證了航天器系統所有狀態量在一定的界內。文獻［18］考慮同時存在外部干擾且發生執行器故障的情況，根據設計的事件觸發機制，提出了一種自適應分布式協同姿態控制律，以確保航天器系統能夠協同追蹤上期望的姿態軌跡，在設計事件觸發機制的過程中，應確保事件觸發間隔恒大于零，否則會看到在有限時間內無限次事件被觸發的Zeno現象［19］。

本文圍繞通信資源受限、液體大幅晃動下的充液航天器姿態控制系統展開研究。本文的創新點在于：①基于描述充液航天器固-液耦合特性的運動脈動球模型，考慮液體大幅晃動產生的非線性干擾，采用自適應更新與滑模控制相結合的策略，估計干擾項的界并進行補償，提高系統的魯棒性。②考慮到充液航天器的通信資源有限，基于事件觸發的思想，設計了與滑模面有關的觸發閾值，根據系統狀態量與滑模面之間的距離決定控制信號的更新，相比傳統的時間觸發機制，可有效減輕控制器與執行器之間的通信負載，實現對通信資源的高效利用。③針對事件觸發與自適應滑模的復合控制方法，設計Lyapunov函數對充液航天器姿態控制系統進行穩定性分析，證明了系統的狀態量將最終一致有界，而且控制輸入的更新頻率得到顯著降低，不存在Zeno現象，平旋機動下的仿真也驗證了該控制策略的可行性。

1 模型描述與控制目標

1.1 模型描述

本文用運動脈動球模型描述充液航天器中液體的大幅晃動，將任意形狀的貯箱等效為球形貯腔，大幅晃動的液體等效為半徑不斷變化的脈動球［20］，如圖1所示。

圖1 充液航天器的模型示意圖Fig.1 Schematic diagram of liquid-filled spacecraft model

在圖1中，本體坐標系Cxyz以貯箱的幾何中心C為原點，相對于慣性坐標系的角速度為Ω，平動速度為VC。航天器剛體部分的質量為M；相對于質心轉動慣性矩陣為I。FE、TE分別為待設計的控制力、力矩；FL、TL分別為液體在貯箱內晃動而產生的干擾力、力矩；rE和rL分別為FE和FL作用點的位置向量。任意形狀的貯箱被等效為球心在貯箱幾何中心的球形貯腔，半徑為R；其質心的位置向量為rT。液體部分被等效為半徑R-r、質量m、始終與貯腔保持接觸的均勻脈動球，兩者的接觸點為Pa。其中，r為脈動球的質心的位置向量rS的模長，e為rS的單位向量。脈動球相對于貯箱的平動速度為VS、角速度為ωS。

下面給出充液航天器姿態控制系統在本體坐標系Cxyz中的動力學方程。其中，航天器剛體部分為

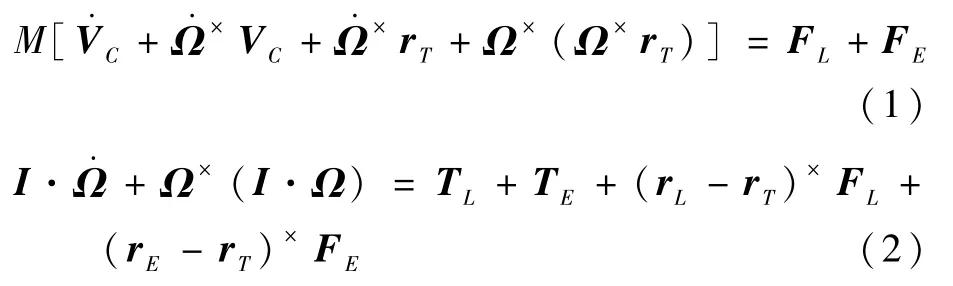
等效為脈動球的液體部分為

在運動脈動球模型中，FL由法向力N e和摩擦力Fb組成，即

式中：ω=e×VS/r為e的轉動速度；σ為液體的表面張力；μ為液體燃料的運動黏性系數；L=R-r為脈動球的半徑。

液體晃動的作用力矩TL的表達式為

式中：Lmin為脈動球的最小半徑，即液體的慣性張量最小時對應的等效半徑；ωr=e·（e·ωS）為ωS沿e的分量；0≤tsr≤1為脈動球繞軸轉動和滾動轉動的權值；ρ為脈動球的密度。

本文中的“×”符號表示若a=［a1a2a3］T，則a×為a的反對稱矩陣：

本文只對充液航天器的姿態控制進行研究，故忽略VC、V·C和式（1）的影響，對式（2）～式（9）進行整理，獲得液體大幅晃動下的充液航天器姿態動力學方程如下：

式中：

進一步簡化，得

式中：J為整個航天器（包括液體部分）的轉動慣量矩陣，由剛體部分固有轉動慣量J0和液體晃動導致的時變轉動慣量ΔJ共同組成，即J=J0+ΔJ，J0=I；u=TE；d為由于液體晃動而作用在充液航天器姿態上的全部干擾力矩。

充液航天器的姿態運動學方程可以表示為

1.2 控制目標

考慮航天器實際的機動情況及下文中對控制器的研究，提出假設：

基于上述假設，針對式（13）和式（15）所描述的航天器姿態控制系統，考慮液體大幅非線性晃動，以及有限的通信資源，設計姿態控制器u，實現姿態四元數q→［1 0 0 0］T，角速度Ω→［0 0 0］T。

2 控制器設計

圖2為本文設計的事件觸發姿態控制系統［15，21-22］。傳感器、控制器及執行器通過網絡進行信息融合。為了實現網絡通信資源的高效利用，在控制器端加入設計的事件觸發，對于傳感器測量得到的狀態量信息，在姿控模塊進行在線計算，滿足觸發條件的控制輸入才會被傳輸到執行器，這樣可減少控制信號傳輸對通信網絡的資源占用。

圖2 事件觸發機制的姿態控制系統框圖［15，21-22］Fig.2 Attitude control system block diagram of event-triggering mechanism［15，21-22］

首先結合控制目標，對于單位四元數描述的姿態控制系統，設計滑模面為

式中：K=diag（K1，K2，K3），Ki＞0，i=1，2，3。

控制信號為

式中：v（t）為待設計的控制信號；tk指第k次觸發事件的時刻。

相比固定閾值的事件觸發機制（觸發閾值為恒定的數值，不發生改變），相對閾值的事件觸發機制（隨狀態量發生變化）可以進一步地減小事件觸發的頻率，提高通信資源的利用率。而在滑模控制器的設計過程中，控制輸入需要讓狀態量先收斂到滑模面上，繼而能夠收斂到平衡點。因此，選擇與滑模面相關的觸發閾值，既有利于控制性能的保證，又能實現通信資源的節約［23］。當系統的狀態量離滑模面的距離較大時，相應地，觸發閾值也大，觸發間隔長，通信負載低；當與滑模面的距離較小時，相應地，觸發閾值也小，控制輸入精準更新，控制精度高。故事件觸發機制為

式中：u（t）=v（tk），tk≤t＜tk+1；k1＞0；0＜α＜1；χ＞0。

對滑模面（16）求導，并代入式（13）和式（15）。

引入向量D，得

綜合上述不等式，可以得到

根據滑模面的定義（16）和單位四元數的性質，得

所以

通過以上分析，基于滑模控制與自適應控制理論，設計如下控制器：

定理1針對充液航天器姿態控制系統（13）和（15），考慮由液體晃動導致的轉動慣量不確定性和干擾力矩，以及有限的通信資源，在假設1、假設2的條件下，基于事件觸發機制（18），設計式（28）所示的控制律和式（29）所示的更新律，則滑模面（16）可以實現全局一致最終有界穩定，從而實現各狀態量的追蹤誤差最終收斂在一定的界內，并且避免Zeno現象的發生。

證明選取如下Lyapunov函數：

對式（30）進行求導，可以得到

將式（19）代入式（31），可以得到

將控制律（28）代入到式（32），可以得到

由式（43）可知，當

將更新律（29）代入到式（34），可以得到

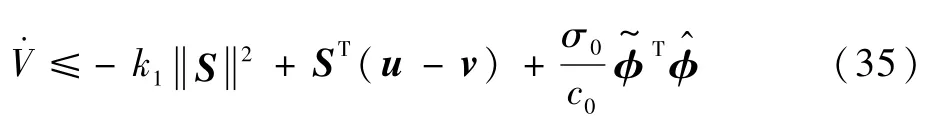
將觸發機制（18）代入到式（35），可以得到

定義η，0＜η＜k1（1-α），則

式中：

所以，

根據式（40），事件觸發下的自適應滑模控制器能夠使得整個系統的狀態量最終一致收斂到邊界內，其界為

基于邊界（41），定義新的Lyapunov函數：

對Lyapunov函數求導，得

為證明避免Zeno現象，此處還需證明?k∈Z+，存在T＞0，使得tk+1-tk＞T。當t∈［tk，tk+1）時，

式中：

對控制輸入v進行求導，得

所以

故式（47）可以表示為

又因為

故ξT＞k1χ，T＞k1χ/ξ，即事件觸發間隔嚴格恒大于0，所以能夠排除Zeno現象的出現，不會在有限時間內觸發無限次事件。證畢

3 仿真校驗

本文以Sloshsat衛星為仿真對象，在初始時刻繞其最大慣性主軸旋轉。在0～33 s內施加力矩，使得其繞中間慣性主軸旋轉［20］。這種平旋機動下，衛星旋轉角速度較高且姿態變化較快，很容易激起液體的大幅晃動。在33 s后開始施加控制力矩，分別對自適應滑模控制策略和本文提出的事件觸發與自適應滑模的復合控制策略展開仿真對比。

2）脈動球的參數取值如下：m=33.5 kg，VS=［0 0 0］Tm/s，ωS=［0 0 0］Trad/s，RS=［0.1 0 0］Tm，R=0.351m，Lmin=0.22m。

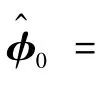
2種控制方法下的充液航天器角速度、姿態四元數、控制力矩及事件觸發間隔的變化曲線分別如圖3～圖6所示。

從圖3的角速度變化曲線可以發現，2種控制策略下的角速度變化趨勢一致，收斂相同、精度相似，約2×10-4rad/s。由于事件觸發機制的存在，角速度變化的平滑性降低。

從圖4中的姿態四元數變化曲線可以發現，2種控制策略下，姿態四元數均在100 s左右收斂，精度約為5×10-4。

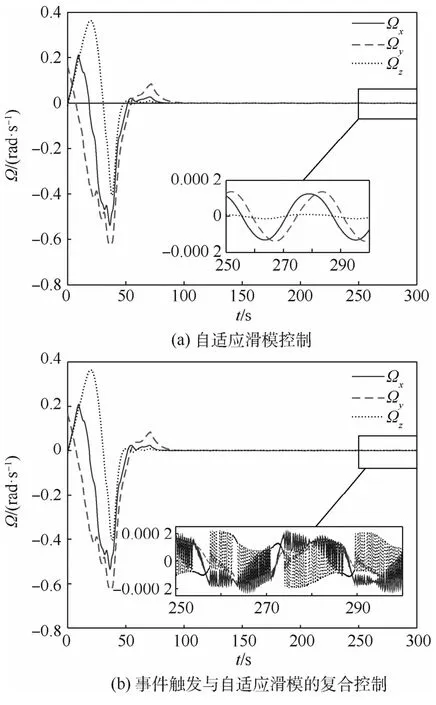
圖3 航天器的角速度變化曲線Fig.3 Curves of spacecraft angular velocities

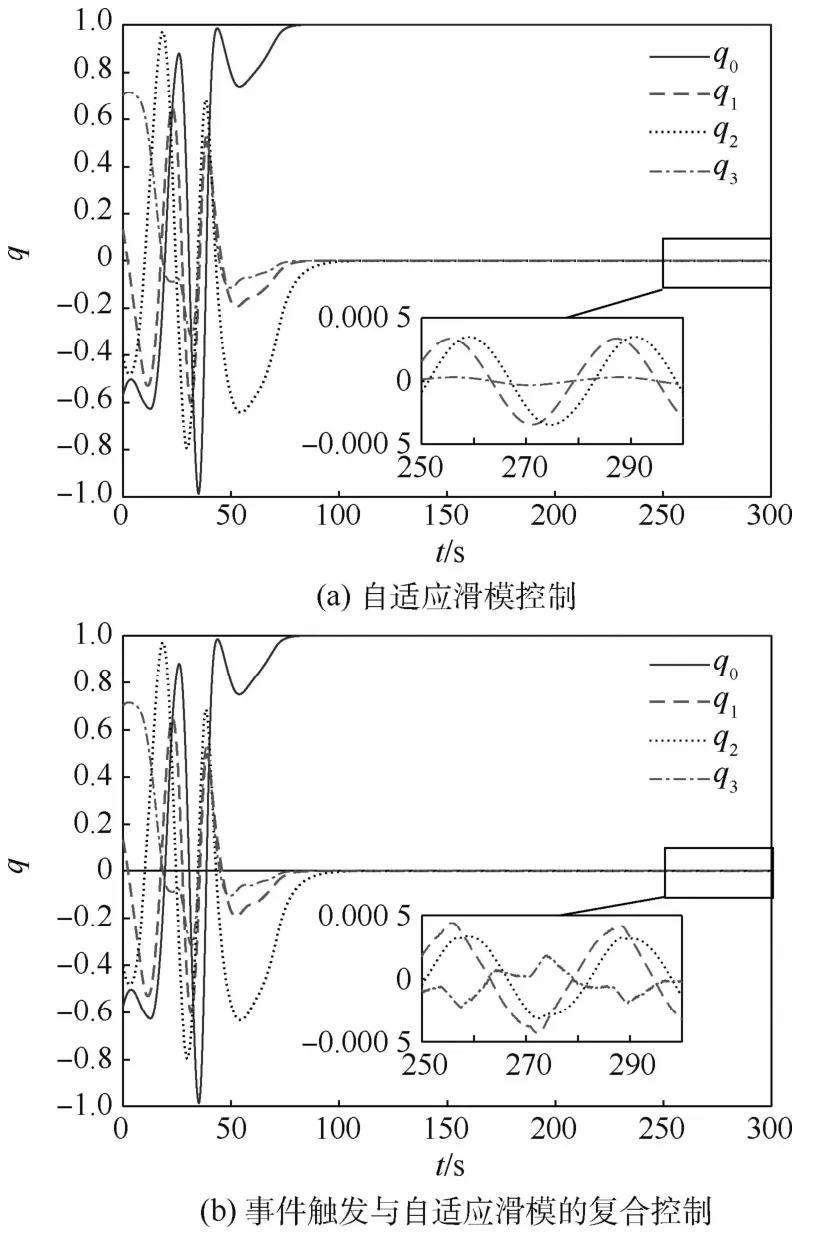
圖4 航天器的姿態四元數變化曲線Fig.4 Curves of spacecraft attitude quaternions

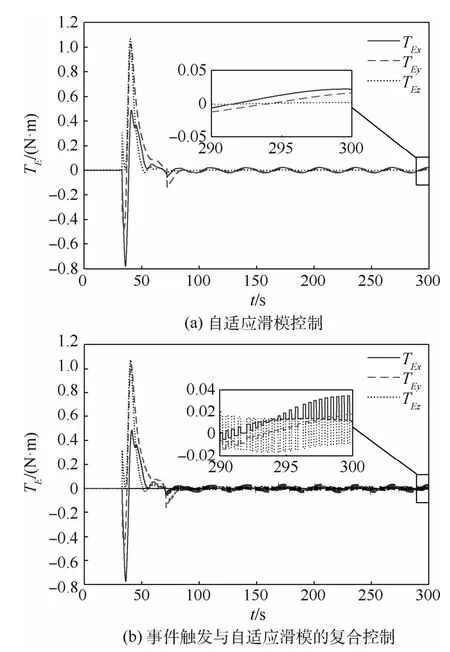
圖5 航天器的控制力矩變化曲線Fig.5 Curves of spacecraft control torques

從圖5和圖6中可以看出，事件觸發與自適應滑模的復合控制策略，只在滿足事件觸發條件的時刻更新控制信號，其他時刻控制量保持不變。在時長300 s、步長0.01 s的仿真中，控制輸入從第33 s開始更新，共計觸發事件878次，平均每0.32 s觸發一次事件，所需通信資源只有自適應滑模控制策略的4%不到，就可實現對航天器姿態系統的有效控制。

圖6 事件觸發的時間間隔Fig.6 Event-triggering interval

4 結 論

1）充液航天器系統具有強耦合、非線性的特點，在液體大幅晃動時更為顯著。滑模變結構控制與自適應更新律相結合的策略，在液體大幅晃動時，依然能實現充液航天器姿態控制系統的各狀態量的一致有界性。

2）在控制器與執行器之間引入事件觸發機制，控制信號的更新閾值與滑模面有關，兼顧對控制精度和通信資源利用率的考量。可有效減少控制輸入的更新次數，釋放更多的通信資源。

3）基于Lyapunov函數的理論分析與平旋機動下的仿真，表明本文提出的控制器既能實現系統各狀態量收斂至較小的界內，也能有效地減小通信頻率，避免對通信資源的浪費。