基于Bisquare 算法的自適應數據采集策略

蔣明佑

(重慶交通大學機電與車輛工程學院)

傳感器數據采集過程中，由于工業現場電器環境惡劣，不可避免的會產生量化噪聲或隨機噪聲[1-8]。在噪聲數據過多的采集任務中，離群數據[9]會影響一元線性回歸模型的擬合過程，降低模型準確度。文章提出了基于Bisquare 算法的自適應數據采集方法，該方法根據數據點的離群程度，對每個數據點分配權值，通過權值分配降低噪聲數據點產生的影響。通過迭代加權最小二乘法實時更新一元線性回歸模型，大大提高了系統采集時間間隔的變化敏感度。通過設置模型置信區間，實現系統對噪聲數據的剔除。文章使用LabVIEW[10]對基于Bisquare 方法的自適數據采集算法進行了仿真試驗，并給出了基于Bisquare 方法的自適應數據采集和依托最小二乘法的自適應數據采集兩者的性能比較結果。

1 數據設計

為了較為準確地模擬傳感器采數據特性，文章基于LabVIEW 設計了幅值為5 的服從正態分布的最優數據源，每秒輸出101 個數據點。將此數據源作為傳感器所采集數據的最優數據源，如圖1 所示。

最優數據源對應函數如下：

其中x 取值范圍為[1，7]。

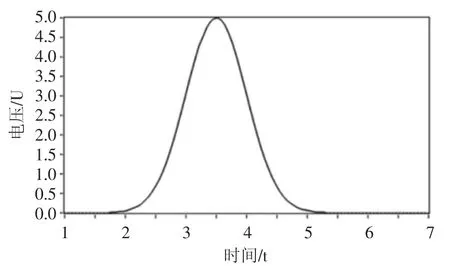
圖1 最優數據源

通常采集測量任務中，大部分噪聲均具有隨機性，其幅度隨時間無規律變化。為模擬真實傳感器采集及數據傳輸時各種噪聲對采集過程的影響，在原有最優數據源基礎上添加了高斯白噪聲及均勻白噪聲。如圖2所示。

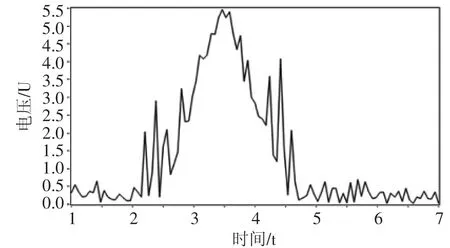
圖2 添加噪聲后的標準數據源

2 最小二乘法自適應采集

2.1 采集策略

基于最小二乘法的自適應數據采集的采集策略可分為兩步：一，掌握數據變化情況。二，動態調整各個采集點之間的時間間隙。其中數據變化情況是系統結合有限個歷史采樣點，通過最小二乘法擬合一元線性回歸模型來反應的。當數據發生變化時，對應的回歸模型也相應發生變化。文章所提的依托最小二乘法的自適應采集中，通過擬合模型中斜率值的變化來調整采集時間間隔。

2.2 最小二乘法自適應采集工作原理

依托模型斜率調整采集時間間隔的最小二乘法自適應采集，其工作原理為：1）系統會結合有限個歷史采樣點，通過最小二乘法構建一元線性回歸模型。

設有s1（x1，y1），（x2，y2）…sn（xn，yn）有限歷史采樣點，最小二乘法擬合如下：

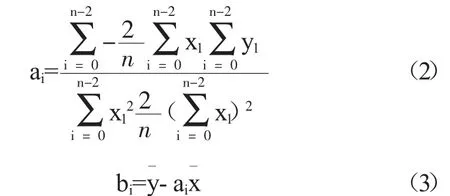
通過上式得到了一元線性回歸模型，將此過程迭代進行，獲得實時變化的擬合模型，即通過模型掌握了數據變化情況。

圖3 示出最小二乘法擬合模型與最佳信號源的對比效果。受噪聲數據影響，在數據急劇變化時，模型擬合效果相對于最佳信號源具有一定偏差。這會導致系統在確定采集時間間隔時出現偏差，進而影響數據采集量，導致關鍵數據缺失。

圖3 最小二乘法與最佳信號擬合模型對比效果

通過此方法，當擬合模型發生變化時，系統的采集時間間隔會根據所設區間發生變化，實現了自適應采集，效果如圖4 所示。

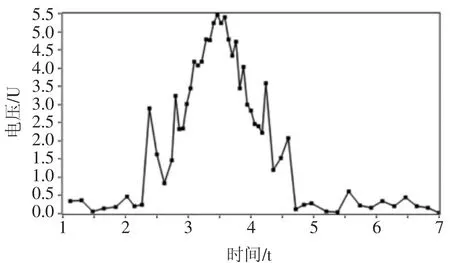
圖4 最小二乘法自適應采集效果

從圖4 可以看出，在區間[1，2]內，數據變化平穩，系統采集到5 個數據點。在區間[2，3]內，數據變化加快，系統采集到11 個數據點。在區間[3，4]內，數據變化最為劇烈，系統采集到17 個數據點。這表明依托最小二乘法，依靠擬合模型斜率調整采集時間間隔的系統具有自適應采集能力。但也可以看出在區間[2，3]和[4，5]內，由于系統對所有數據點等權重看待，所以即使采用變化時間間隔的采集方式也無法完全過濾掉噪聲數據。

3 基于Bisquare 的自適應采集

3.1 采集策略

在掌握數據變化情況方面，此采集策略通過Bisquare[11]算法建立一元線性回歸模型，由模型感知數據變化情況。Bisquare 方法在原有最小二乘法基礎上為每個數據點分配了權重，其中賦予每個數據點的權重取決于該點距離擬合模型的距離，在擬合模型附近的數據點獲得較高權重，遠離擬合模型的數據點獲得較低權重。通過Bisquare 算法很好的降低了噪聲數據對擬合模型的影響，提高了模型準確度。此采集策略通過擬合模型斜率動態調整采集時間間隔，當斜率超過某個設定值時，系統調用對應的采集時間間隔。

3.2 噪聲過濾

基于Bisquare 的自適應采實現了對離群噪聲的過濾，原理如圖5 所示。系統在已有的Bisquare 擬合模型基礎上，在模型兩端設置上下限，上下限閥值ε 可按需而定。當數據點落入區間以內時，如點s1，s2系統將按照指定采集時間間隔對數據點進行采集；對于落入區間以外的點，如點s3系統將不予采集。通過此方法，算法實現了對變時間間隔采集時離群噪聲數據的過濾。

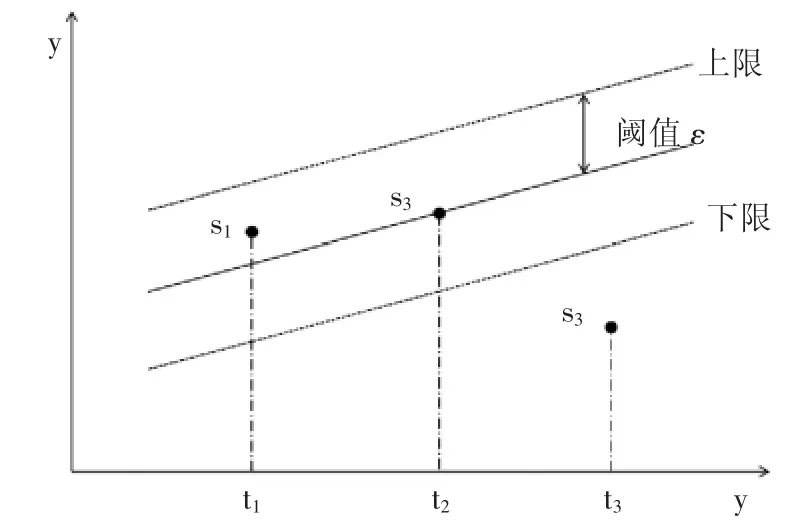
圖5 噪聲過濾原理

3.3 Bisquare 自適應采集工作原理

該算法首先通過最小二乘法對最近有限個離散數據點s2（x2，y2），（x1，y1）…sn（xn，yn）做線性擬合，得到最初擬合模型的斜率與截距的估計值ai與bi，其中i=0，n 為y 的長度。

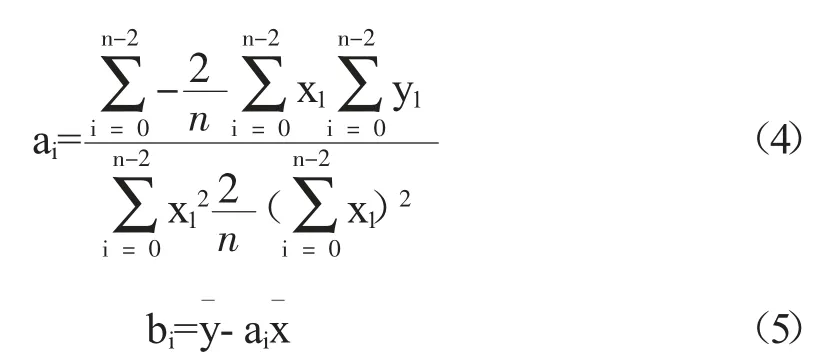
然后通過殘差最小化的方法獲得權重的更新值。Bisquare 算法的殘差計算公式如下，其中wi為對應數據點的權重，fi為對應數據點的最佳擬合值。

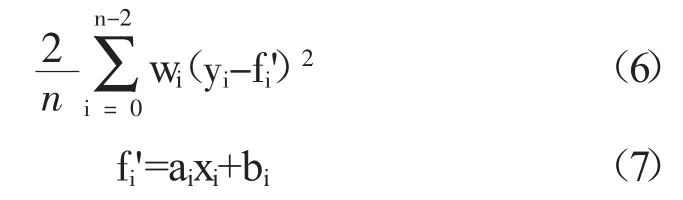
結合已知a0和b0，通過殘差最小化，將上式對ai求導并等于零，可得。

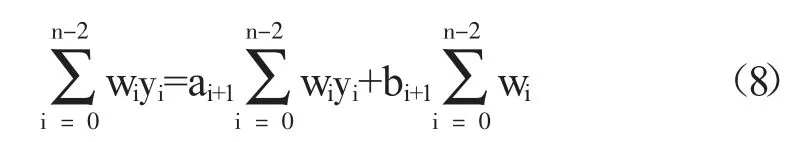
使用新獲得的權重wi做加權最小二乘法，求得ai+2與bi+2：

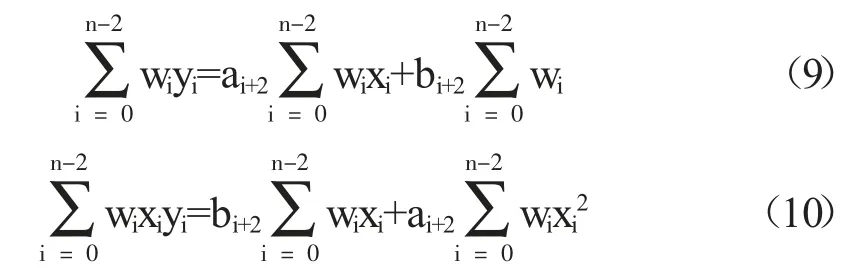
迭代以上過程，當迭代前后兩次擬合多項式斜率與截距的相對差小于容差時，默認為獲得最佳擬合模型，輸出最佳擬合斜率，容差設置為0.000 1。

表1 斜率與采集時間間隔對應表

基于Bisquare 自適應采集時間間隔的確定流程，如圖6 所示。

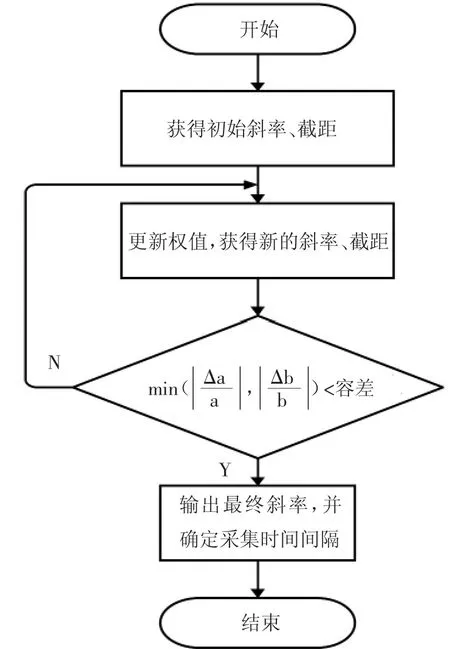
圖6 采集時間間隔確定流程

獲得最佳擬合模型后，系統根據最佳擬合模型斜率確定下次采集時時間間隔。在下次采集過程中，通過將最佳擬合模型上下限與標準數據源做差值處理，差值大于0 的點（即離群數據點）將被剔除。采集過程中離群點的確定，如圖7 所示。

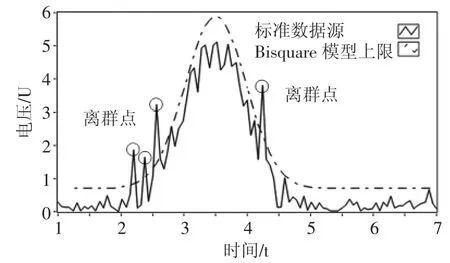
圖7 離群點確定

圖8示出Bisquare 擬合模型與最佳信號源的對比效果。Bisquare 算法很好的降低了噪聲數據對擬合模型的影響。從圖8 可以看出，Bisquare 擬合模型的數據走勢與最佳信號源高度吻合，可以準確反映數據變化情況。

圖8 Bisquare 擬合模型與最佳信號源擬合模型對比效果

通過基于Bisquare 的自適應采集方法，系統同樣實現了具有自適應效果的變時間間隔采集，效果如圖9所示。

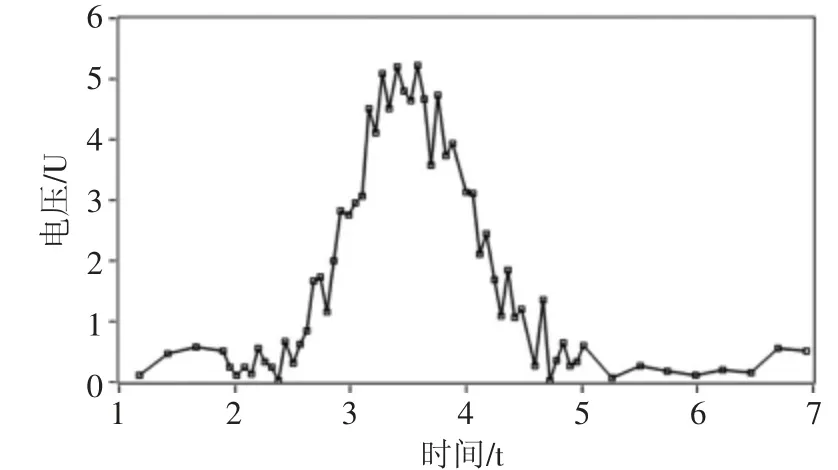
圖9 Bisquare 自適應采集效果

從圖9 可以看出，在區間[1，2]內，數據變化平穩，系統采集到5 個數據點。在區間[2，3]內，數據變化加快，系統采集到15 個數據點。在區間[3，4]內，數據變化最為劇烈，系統采集到17 個數據點。這表明基于Bisquare 算法，系統具有依照模型斜率調整采集時間間隔的能力。另外，系統過濾掉了離群噪聲，所采集數據更加準確反應設備工況。

4 最小二乘法與基于Bisquare 的自適應采集性能比較

針對圖2 提出的標準數據源，分別使用最小二乘法的自適應采集與基于Bisquare 算法的自適應采集進行試驗。試驗采集效果對比，如圖4 和圖9 所示。

其中，使用最小二乘法自適應采集工作60 s 后，系統保存3 240 個數據點，對比傳統的等時間間隔采集，數據量降低了46%；使用基于Bisquare 的自適應采集工作60 s，系統保存3 840 個數據點，對比傳統的等時間間隔采集，數據量降低了37%。

2 種采集方式都減少了數據量的存儲，減緩了系統存儲壓力。但是最小二乘法自適應采集的數據存儲量更低，這是由于擬合模型不準確造成的。受噪聲數據影響，導致在[2，3]和[4，5]內，最小二乘法擬合模型斜率偏低，采集時間間隔增大，因此最小二乘法自適應采集相比于基于Bisquare 的自適應采集，所采集到的數據點更少。

最小二乘法自適應采集失真度相對較高。采用最小二乘法的擬合模型無法區分噪聲數據，可以看到，圖10 中有明顯的離群噪聲點。在噪聲較多的數據區間，模型失真度較高。Bisquare 自適應采集通過權重分配的方法將離群噪聲影響降到最低，所得擬合模型更加接近于最優數據源。模型對比效果，如圖10 所示。

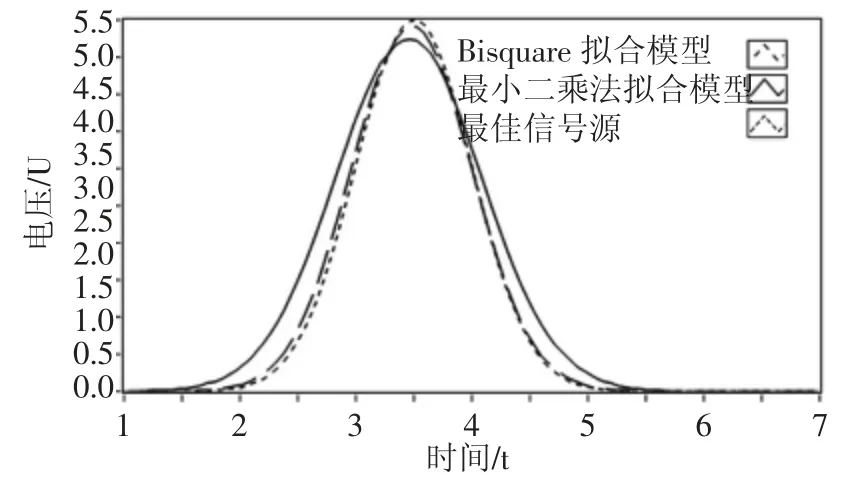
圖10 最小二乘法與Bisquare 擬合模型對比效果

對于2 種方法的采集失真度，可以用2 種方法各自所得數據曲線fi'（x）與fi（x）最優數據源曲線之間所夾面積表示。失真度E（n）計算公式為：

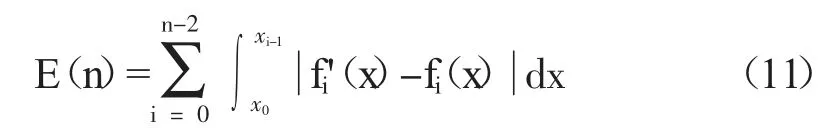
通過計算，同一時刻下，小二乘法的自適應采集的失真度為1.74，基于Bisquare 算法的自適應采集的失真度為1.21。需要說明的是，此試驗的標準數據源時刻在發生變化，因此2 種采集方法的失真度也在變化。

在1 min 的采集試驗內，基于Bisquare 算法的自適應采集平均每個數據點失真度比小二乘法的自適應采集失真度低0.34。

5 結論

文章提出了一種可以通過對數據點分配權重進而降低噪聲影響的自適應采集方法。通過計算機仿真試驗證明，在相同數據源的前提下，該方法在減少數據采集量的同時，可以更好地降低噪聲數據對采集過程的影響，降低數據采集失真度。對比最小二乘法的自適應采集，該方法的失真度明顯小于最小二乘法的自適應采集。通過采用此采集策略，數據采集失真度更小且數據存儲量更低。后期可繼續將Bisquare 算法進行優化，提高算法在無噪聲條件下的應用效果。