PCA 算法在銀屑病BP 神經網絡建模中的應用研究
詹秀菊
(廣州中醫藥大學醫學信息工程學院,廣州510006)
0 引言
銀屑病是一種多因素的慢性炎癥性疾病,病程較長,有易復發傾向,有的病例幾乎終生不愈。據報告,我國目前銀屑病患病率為0.4%,估計有600 余萬患者,歐美國家發病率高于黃種人和黑種人[1],歐洲的患病率為2%-3%[2]。該病發病以青壯年為主,對患者的身體健康和精神狀況影響較大。臨床表現以紅斑、鱗屑為主,全身均可發病,以頭皮、四肢伸側較為常見,多在冬季加重,導致患者出現身體形象以及心理的問題,進而影響患者的正常生活[3]。
英國統計學家卡皮·皮爾遜提出的PCA 算法將多指標化為少數綜合指標的一種統計分析方法[4]。其基本思想是將原有較多變量線性組合轉變為少數新變量來壓縮原有數據矩陣的規模,進而從高維屬性中挖掘出含有信息量最大的影響因子,揭示事物的本質[5]。本研究主要利用PCA 算法將輸入變量降維,用較少的計算量來選擇變量,獲取最佳變量子集合,從而減少BP神經網絡預測模型的運行時間。
1 PCA算法運行步驟
PCA 算法具體步驟如下:
(1)構建樣本矩陣為X={x1,x2,x3,…xn},其中n 表示樣本矩陣的列數,每一列數據代表一個樣本維度。
(2)構建協方矩陣:

(3)計算協方矩陣Cov 的特征值和特征向量,將特征值按照單調遞減排序λ1≥λ2≥λ3…λn,與之對應的特征向量為w1,w2,w3…wn。
(4)選取前k 個特征向量組成矩陣w。

(5)求取主成分Z。
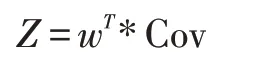
(6)計算主成分貢獻率以及累計貢獻率。

一般選取累計貢獻率達到85%以上的主成分因子作為樣本判別的主要影響因子,作為輸入變量。
2 數據的采集與清洗
(1)文獻數據的采集
將文獻中的文獻題目、發表時間、第一作者、證型、中醫癥狀、收錄范圍、期刊名稱以及治療方法等信息復制到Excel 2016 工作表中,如圖1 所示。

圖1 文獻信息表
(2)癥狀變量選取
選取與銀屑病相關的皮損癥狀、全身癥狀、舌象以及脈象癥狀指標作為輸入變量,其中皮損癥狀有皮疹發展迅速、皮疹經久不退、皮疹消退、皮損鮮紅(紅)、皮損淡紅、皮損暗紅、點滴狀皮疹、斑片狀皮疹、地圖狀皮疹、鱗屑干燥脫落、鱗屑附著緊、皮損肥厚、浸潤明顯、皮膚干燥、皮膚潮濕、皮損灼熱和皮損腫脹等17 個癥狀,全身癥狀有疲乏、咽干、咽燥、咽腫、咽喉痛、肢體倦怠、頭暈、胸悶、納呆、喜冷飲、口干、口渴、口苦、失眠多夢、不寐、心煩易怒、便干、便秘、便溏、小便黃赤和唇青紫等21 個癥狀,舌象有舌紅、舌紫暗、舌暗紅、舌淡紅、瘀斑、苔黃、苔白、苔薄、少苔、舌燥和苔膩等11 個癥狀,脈象有浮脈、沉脈、緩脈、數脈、澀脈、滑脈、弦脈、細脈和濡脈等9 個癥狀。
(3)證型變量選取
趙炳南老中醫將銀屑病分為血熱型、血燥型、血瘀型三型辨證治療,朱仁康認為銀屑病可分為血熱型、血燥型、風濕型、毒熱型[6]。周鳴岐等根據銀屑病的病例特點將其分為風熱血熱與風熱血燥兩型[7]。本研究證型的選取參考《尋常型銀屑病(白疕)中醫藥臨床循證實踐指南2013 版》[8],選取血熱型、血燥型、血瘀型等三型為輸出變量。
(4)數據歸一化處理
數據挖掘的前提是數據歸一化處理,其目的在于將文獻數據轉變為數值類型的數據,有利于機器識別。本研究中自變量X 為癥狀信息,X1,X2,X3,…,X58 分別代表58 個癥狀變量。因變量Y 為證型信息,即Y 代表證型。其中癥狀有無分別設置為1、0,血燥型、血瘀型、血熱型分別設置為1、2、3,并錄入到Excel 2016 工作表中,如表1 所示。

表1 數據量化表
本研究篩選符合條件的文獻共445 篇,每篇文獻錄入一條病案,即錄入Excel 文件中病案共445 條。其中輸入變量有皮損癥狀、全身癥狀、舌象和脈象等58個癥狀,輸出變量為血燥型、血瘀型、血熱型。
3 PCA降維
(1)數據準備將銀屑病數據保存為名為sheji1.xls 的Excel 文件,利用MATLAB 2015a 軟件中xlsread()函數讀取數據,將讀取的數據命名為data1,讀取data1 中1 到58列作為輸入數據命名為input,讀取data1 中第59 列數據作為輸出數據命名為output。具體代碼如下:

(2)算法參數設定
PCA 算法的累計貢獻率變化對BP 神經網絡性能具有一定的影響,為了準確、迅速地選取累計貢獻率,PCA 算法的累計貢獻率在80%到100%之間選取。本研究利用MATLAB 2015a 自帶工具箱實現PCA 降維的功能,代碼如下所示,以BP 神經網絡預測模型的準確率及運行的時間為判斷指標,比較BP 神經網絡與PCA-BP 神經網絡的準確率、時間,選取PCA 參數最合適的累計貢獻率。
實現PCA 模型參數設定的核心代碼如下:


如圖2 所示,從圖形上可看出,PCA-BP 神經網絡模型的運行時間大部分是小于BP 神經網絡模型的運行時間,除了當累計貢獻率為0.95 時,該累計貢獻率可刪除,不選取該值作為PCA 算法的參數值,整體結果可說明PCA 算法能夠減少BP 神經網絡運行時間。當累計貢獻率為0.83、0.84、0.85、0.86、0.88、0.90、0.93、0.94、0.96、1 時,PCA-BP 神經網絡模型的準確率大于BP 神經網絡模型的準確率,收集以上符合條件的累計貢獻率匯總為一個表,如表2 所示,從表中可看出準確率排名前五的累計貢獻率有0.83、0.85、0.88、0.84、0.93,其相對應的準確率分別為0.92、0.90、0.86、0.86、0.85。PCA-BP 神經網絡模型運行的時間排名前五的累計貢獻率有0.93、0.90、0.85、0.88、0.84,其對應的運行時間分別為0.78、0.88、0.95、0.98、1.03。綜合各種因素考慮,PCA 的累計貢獻率設置為0.93,PCA-BP 運行時間為0.78,準確率為0.85。

表2 累計貢獻率表

圖2 PCA參數運行圖
(3)結果分析
PCA 模型根據上面可確定累計貢獻率設置為0.93,運行以下代碼,可得出各個因子的貢獻率以及累計貢獻率,且各因子的貢獻率按降序排列,如表3 所示,從表中可看出第34 個主成分因子的累計貢獻率為0.9267,第35 個主成分因子的累計貢獻率為0.9329,因累計貢獻率參數設置為0.93,即提取前面34 個主成分因子作為BP 神經網絡模型的輸入變量。
實現PCA 降維的代碼如下:


表3 主成分因子貢獻率
綜上所述,PCA 算法具有提取決定性作用指標的特性,以減少計算工作量。本研究PCA 算法的累計貢獻率設置為93%,將58 個癥狀輸入變量變成34 個主成分因子,以減少BP 神經網絡預測模型的運行時間,實驗結果也證明PCA 算法具有消除冗余的特征,減少了銀屑病BP 神經網絡預測模型運行時間,提高模型的運行效率。

