基于QR-m-GARCH(1,1)-GED模型的人民幣匯率隔夜風險測度

張建文, 唐國強, 楊靜凌

(桂林理工大學 理學院, 廣西 桂林 541006)

0 引 言

在經濟全球化盛行的大背景下, 各國經濟發展緊密相連。 作為世界第二大經濟體的中國, 更是深深融入到世界之中。 在當代中國， 經濟全球化很重要的一個標志就是人民幣國際化。就目前的國際金融體系來看, 全球已經有40多個國家把人民幣作為儲備性貨幣。隨著中國國際地位的提高和匯率市場改革的完善, 人民幣的國際影響力不斷提升[1]。近年來， 國際經濟形勢風云詭譎, 人民幣匯率面臨較強的升值壓力。一旦人民幣匯率發生大的波動, 將嚴重危害我國經濟市場的平穩發展。人民幣匯率波動的增加, 顯著減小中國企業對外投資的可能性, 對銀行業超額收益產生負向影響[2-3]。因此, 深入研究人民幣匯率風險, 進而實現風險的防控與管控, 對我國經濟市場平穩運行具有重大意義。

人民幣匯率整日風險嚴格意義上可以分為日內風險和隔夜風險。其中, 隔夜風險是指前一天收盤到第二天開盤期間價格波動引發的風險, 但由于風險值較低, 只引起了小部分學者關注： 彭偉[4]提出了隔夜-AS模型和隔夜-SAV模型對隔夜風險進行測度； 簡志宏等[5-6]使用CAViaR-EVT模型分別在左、 右尾分位數下對極端情況下的隔夜風險進行預測, 并采用HAR-CJ-M模型對高頻數據進行隔夜風險的波動研究, 實現了隔夜風險的可預測。以上文獻雖對隔夜風險進行了一定研究, 但隔夜風險作為整日風險的一部分， 極其隱蔽, 目前實證研究文獻相對較少, 亟待豐富。本文基于QR-m-GARCH(1,1)-GED模型對人民幣匯率隔夜風險進行研究, 既豐富在該方面的研究方法, 又豐富了研究內容。

金融領域的學者將VaR(風險價值)作為風險的測度指標, 故本文將其作為度量人民幣匯率隔夜風險大小的指標, 在實際運用中, 學者們常借助GARCH類模型求解VaR值。申利[7]使用GARCH(1,1)模型推算人民幣兌美元匯率數據的動態VaR； 申世昌等[8]使用GARCH類模型研究健康險收益率的波動性, 并對中國健康保險市場的VaR值進行度量； 曾裕峰等[9]以滬深300股指期貨為研究對象, 使用GARCH模型求解VaR值, 發現廣義誤差(GED)分布相比正態分布和t分布風險的預測精度更優； 李世君等[10]采用偏t分布下的GARCH模型對消費行業的5個板塊指數進行VaR求解, 失敗率檢驗結果表明模型擬合效果較好。雖然使用GARCH類模型進行風險度量在金融市場已得到廣泛應用, 但隨著研究的深入, 也暴露出模型缺點。

GARCH模型需要預先設定誤差服從的分布, 在一定程度上從模型自身角度加大了誤差。由于分位數回歸(quantile regression, QR)理論優良的統計特征, 部分學者開始將GARCH模型和分位數回歸模型進行組合引入VaR的建模求解。陳耀輝等[11]采用QR-GED-GARCH模型和GED-GARCH模型對人民幣匯率收益率風險進行測度, 將二者的擬合成功率進行比較, 發現QR-GED-GARCH模型更適合描述人民幣匯率的數據特征； 涂振興[12]采用歷史模擬法、 QR-GARCH模型、 Gumbel Copula函數法, 對證券市場的4個指數進行研究發現， QR-GARCH模型更適宜刻畫我國證券市場波動現象； 劉亭等[13]研究滬深綜合指數的收益率數據, 建立QR-t-GARCH(1,1)模型與QR-st-GARCH(1,1)模型對指數收益率的風險特征進行全面描述； 王傳美等[14]針對創業板的隔夜收益數據, 使用GARCH類模型與QR-GARCH類模型求解VaR, 發現QR-GARCH類模型得到的結果更準確。以上研究均表明, 將分位數理論與GARCH類模型組合后的模型能夠較好地描述數據特征, 度量得到的風險結果更準確。

本文使用GARCH類模型與分位數回歸模型的組合模型對人民幣匯率進行隔夜風險的測度。由于美元指數在人民幣匯率隔夜風險產生期間發生了完整的交易, 因此在GARCH類模型的均值方程中加入美元指數作為人民幣匯率隔夜收益率的解釋變量, 從中選取最優模型與分位數回歸模型進行組合研究人民幣匯率隔夜風險, 最終建立QR-m-GARCH(1,1)-GED模型求得VaR值, 同時將常數均值方程的QR-GARCH(1,1)-GED模型作為對照, 比較二者擬合成功率。

1 理論介紹

1.1 GARCH族模型

ARCH模型最早由Engle[15]于1982年提出, 但針對具有長期自相關性的數據進行擬合時, 會產生很高的移動平均階數, 增加模型估計的難度， 從而影響ARCH模型的擬合精度。此后Bollerslev[16]在ARCH模型的基礎上進行推廣, 假設條件方差不僅受滯后一階平方擾動項的影響, 而且受自身一階滯后項的影響, 即廣義ARCH模型——GARCH模型。低階的GARCH模型已可以實現大部分非線性條件方差的刻畫, 故使用GARCH(1,1)模型擬合人民幣匯率隔夜收益率數據, 模型如下:

(1)

ut=σtεt；

(2)

(3)

將美元指數日對數收益率mt作為解釋變量, 對應的均值方程如下

rt=at1mt+ut,t=1,2,…,T。

(4)

其中,at1表示美元指數變量前系數。

為彌補GARCH模型不能區分好、 壞消息給金融市場帶來的不同影響, 學者們相繼提出了非對稱沖擊模型, 如TARCH、 EGARCH、 PARCH模型。

TARCH模型是Glosten等[17]提出的, 可以衡量好消息和壞消息對條件方差帶來的不同沖擊, 并且可以檢驗數據是否具有杠桿效應。非對稱模型的均值方程與GARCH模型相同, 不再重復列出, 僅將條件方差方程列出

(5)

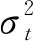
EGARCH模型[18]又稱為指數GARCH模型, 設定標準差與誤差項之間滿足更靈活的指數關系， 對應表達式如下

(6)

其中：ω,α,β,γ均為變量前系數。方程通過設定條件方差的對數形式, 反映呈指數函數變化的杠桿效應。

PARCH模型[19]模擬對象不再局限于方差, 而是標準差的δ次方。這樣可以減弱條件方差受到大幅沖擊時帶來的影響。其方程為

(7)

其中：ω,α,β是常數;γ用來描述非對稱效應;δ是標準差的冪指數參數,δ>0， 通過估計得出, 可以描述沖擊帶來的影響幅度。

1.2 VaR及計算方法

VaR指某金融資產在持有期L內, 在顯著性水平α下, 可能遭受的最大損失值。設FL是金融資產L期內損失函數的累積分布函數, 記為FL(x)=P(L≤x)。VaR其實就是FL的α分位數, 表示為[20]

VaRα=inf(x|FL(x)≥α)。

(8)

在VaR值的計算方法中,方差-協方差方法最為流行, 最簡單的就是借助GARCH模型的參數結果進行求解。以持有期1期為例, 給出3種分布下的計算公式。

1) 正態分布

(9)

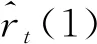
2)t分布

(10)

其中：ν為自由度；tν(α)是對應的α分位數。

3) GED分布

(11)

其中：GEDα,ν,ε是GED分布在自由度為ν下的α分位數。

分位數回歸使用參數估計的方法, 使誤差絕對值的加權之和最小, 不需要假設誤差項的分布, 從模型層面降低了擬合失敗的風險。Taylor[21]將分位數回歸模型引入VaR的求解。在置信水平為(1-α), 持有期為K期的金融資產收益率VaR的計算公式為

Vt,K(α)=β1,α+β2,αK1/2+β3,αK+β4,αK2+

(12)

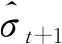
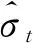
(13)

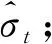
2 實證分析

2.1 數據選取與描述性統計

本文選取人民幣匯率作為研究對象, 選用1美元折合人民幣金額的直接標價法表示匯率價格。實證數據為人民幣匯率和美元指數的每日開盤和收盤價格。數據來源于同花順軟件, 選取的時間為2009-12-10—2019-08-23。

如果將相鄰兩天的收盤價的對數差定義為整日收益率r=lncloset-lncloset-1, 那么可以將其分為兩部分: 日內收益率r1=lncloset-lnopent和隔夜收益率r2=lnopent-lncloset-1。按照上述定義, 根據時間順序, 將人民幣匯率隔夜收益率和美元指數日內收益率的時間關系表示為圖1。美元與中國外匯市場的交易時間規律暗示著美元匯率日內收益的變動可能會對接下來開盤的人民幣匯率產生一定的影響, 從而影響到人民幣隔夜收益率, 即人民幣匯率隔夜風險， 也就是前一天收盤到第二天開盤這段時間會受到美元指數影響的風險。

圖1 人民幣與美元的時間關系

擬合模型前, 先將人民幣匯率序列與美元指數序列的日期進行比對, 剔除不重疊日期對應的數據。針對處理后的數據, 計算人民幣匯率的隔夜收益率和美元指數日內收益率。由于數值量級過小, 為方便參數估計, 將人民幣匯率隔夜收益率序列、 美元指數日內收益率序列放大100倍后再進行研究， 運行結果由Eviews 9.0和R語言實現。

借助人民幣匯率隔夜收益率的時序圖圖2可直觀地分析波動特征。可知, 人民幣匯率隔夜收益率序列圍繞著0值上下波動, 波動幅度在-1.2～1.2, 整體上序列處于平穩狀態。但也觀察到有多次明顯的大幅上升和下降, 說明所選時間段內隔夜風險的確存在且不容忽視。以2015年8月11日匯率改革為分界線, 匯改前人民幣匯率隔夜收益率除幾次大的波動外基本保持平穩, 匯改后波動頻率和幅度明顯加劇。匯率改革提高了人民幣匯率的市場化水平, 增強了外匯市場的透明度, 但也使得匯率的彈性變大。所選取的10年數據中, 2018年人民幣匯率隔夜收益率波動最為劇烈, 這是因為貨幣政策分化和中美貿易戰加大了人民幣匯率的基本面壓力。

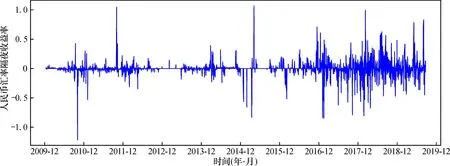
圖2 人民幣匯率隔夜收益率時序圖

為進一步分析人民幣匯率隔夜收益率的數據特征, 對數據進行描述性統計分析, 結果見圖3。人民幣匯率隔夜收益率的均值為-0.001 7, 呈負收益特征; 標準差為0.121 9, 表明人民幣匯率隔夜收益整體波動不大; 偏度為負數, 說明數據整體向左傾斜; 峰度為24.884 8, 遠大于3, 說明數據的“尖峰”特征顯著; J-B統計量為49 657.76, 其對應的p值為0, 表明樣本數據不服從標準正態分布。

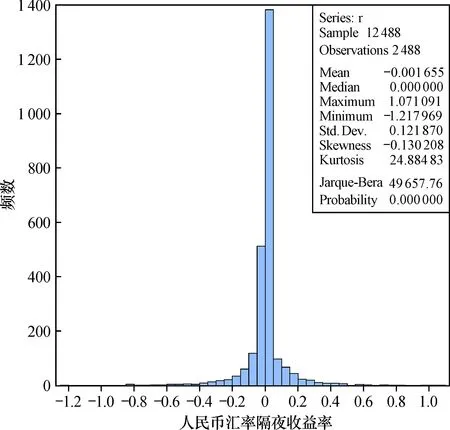
圖3 人民幣匯率隔夜收益率直方圖和基本統計量

2.2 平穩性檢驗及格蘭杰因果關系檢驗

為了從統計角度驗證美元指數會對人民幣匯率的隔夜風險產生影響的猜測, 借助Granger因果關系檢驗驗證二者之間的關系。由于Granger因果關系檢驗對數據有平穩性要求, 故在進行檢驗之前, 先對數據進行平穩性檢驗, 防止出現虛假回歸, 導致檢驗結果的不準確。采用ADF單位根檢驗對美元指數日內收益率與人民幣匯率隔夜收益率進行平穩性檢驗, 結果如表1所示。可以看出, 兩變量單位根檢驗對應的p值均為0, 說明在99%的置信水平下, 人民幣匯率隔夜收益率序列和美元指數日內收益率序列均平穩。

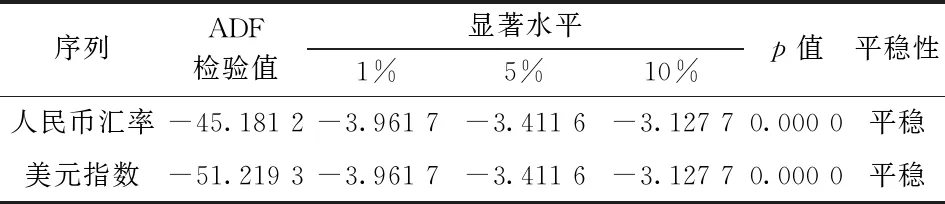
表1 單位根檢驗結果

在兩序列均平穩的前提下, 對人民幣匯率隔夜收益率序列和美元指數日內收益率序列進行格蘭杰因果關系檢驗, 檢驗結果見表2。發現兩個檢驗結論中只有一個拒絕原假設, 說明只存在一個單向格蘭杰因果關系。在1%的顯著性水平下, 美元指數是人民幣匯率的格蘭杰原因, 同時人民幣匯率不是美元指數的格蘭杰原因。這驗證了美元指數日內收益率會影響人民幣匯率隔夜風險的猜測, 證實可以將美元指數日內收益率作為人民幣匯率隔夜收益率數據的解釋變量。這也從側面說明, 中國外匯市場存在被美國外匯市場引導的現象。

表2 Granger因果關系檢驗結果

2.3 ARCH效應檢驗

在建立GARCH類模型之前, 首先要檢驗人民幣隔夜收益率序列是否具有ARCH效應特征。由于要建立兩種不同的均值方程, 加入美元指數日內收益率序列作為解釋變量的均值方程和常數均值方程, 故進行兩次檢驗。使用拉格朗日乘數檢驗, 即ARCH-LM檢驗進行驗證, 滯后1階的ARCH-LM檢驗結果見表3。結果發現, 對應p值均為0, 表明在1%的顯著性水平上拒絕原假設, 說明兩種不同均值方程的殘差序列具有顯著的ARCH效應, 可以建立GARCH類模型。

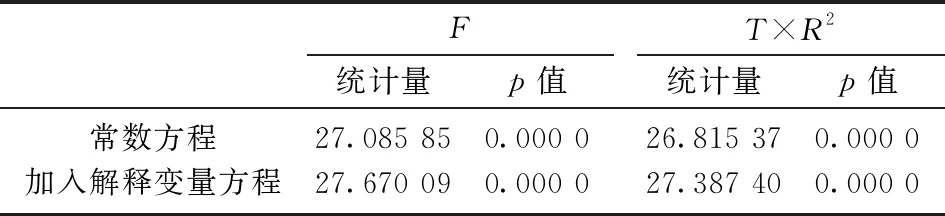
表3 ARCH效應檢驗結果

2.4 模型的建立及VaR的求解

由于人民幣匯率數據存在ARCH效應, 可以建立GARCH類模型來描述數據的“尖峰厚尾”特征, 消除異方差性。為獲取更優的數據擬合效果, 建立4個不同的波動率模型GARCH、 TARCH、 EGARCH、 PARCH進行比較, 從中選出最優模型進一步分析。由于GARCH類模型普適性強, 低階模型就能夠很好地測量數據的時變特征。駱珣等[23]驗證了GARCH(1,1)模型能較好地度量人民幣匯率風險。故選用GARCH(1,1)、 TARCH(1,1)、 EGARCH(1,1)、 PARCH(1,1)模型, 在3種不同的分布(正態、t、 GED)下建模, 通過AIC(Akaike information criterion)和SC(Schwarz criterion)準則從中選出最優模型。由于前文已經證明美元指數是人民幣匯率隔夜收益率數據的格蘭杰因果原因, 故在模型均值方程中加入美元指數收益率數據作為解釋變量, 同時將簡單常數均值方程模型作為對照, 其中誤差服從3種不同的分布, 每種分布對應8個模型, 共建立24種不同的模型, 信息準則結果如表4所示。

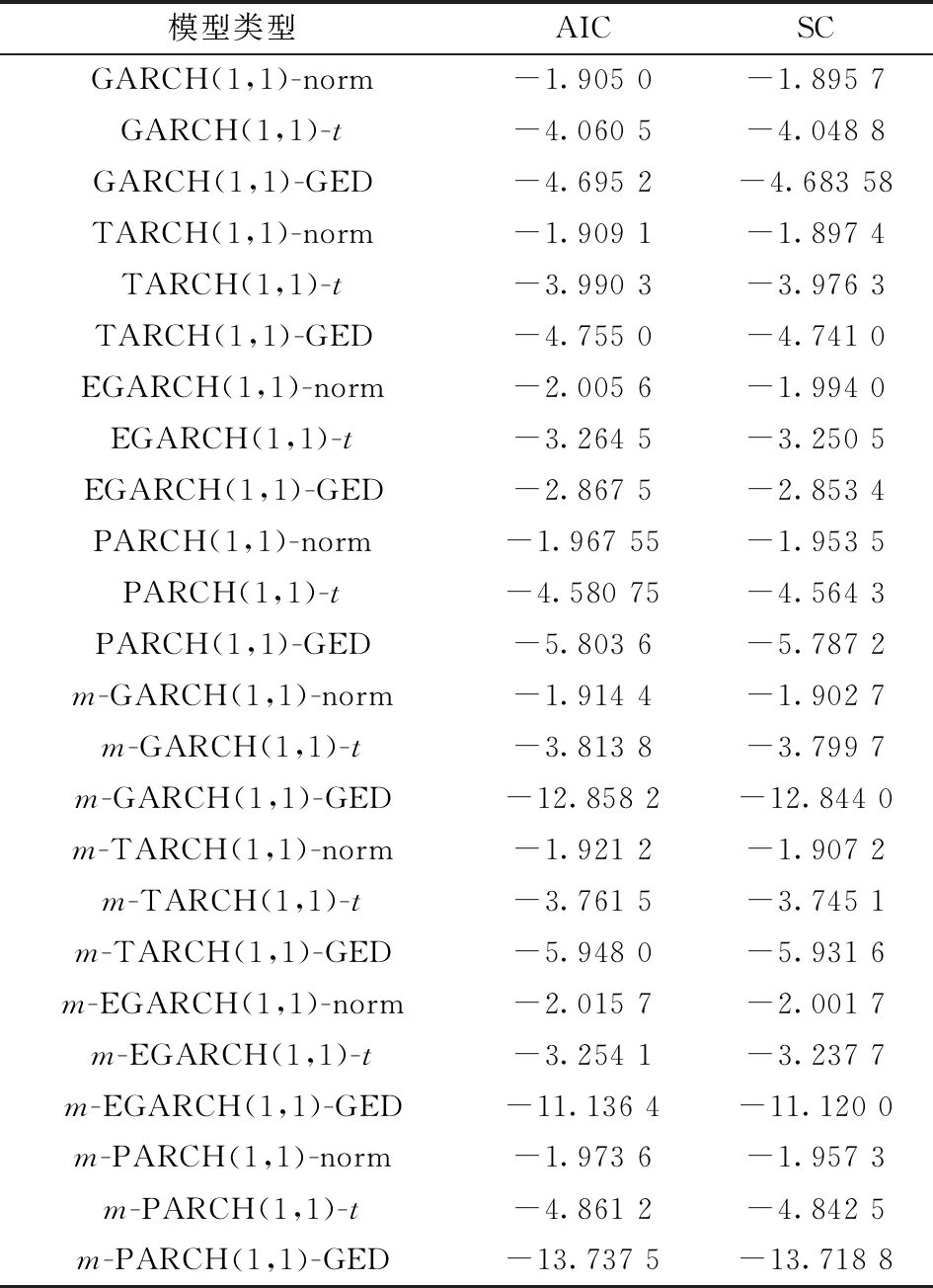
表4 各模型的信息準則結果

從誤差服從不同分布角度分析, 僅有EGARCH(1,1)模型在誤差服從t分布時, 對人民幣匯率隔夜收益率數據的擬合優度高于正態和GED分布。另外7個模型, GED分布比正態、t分布對應的AIC和SC信息準則值更小,擬合優度更高。表明GED分布在測度人民幣匯率隔夜風險的能力要優于正態和t分布。從均值方程角度分析,加入美元指數作為解釋變量的m-GARCH類模型,比簡單常數均值方程的GARCH類模型有更小的AIC和SC值, 且GED分布下兩者差距更明顯。 比如,m-GARCH(1,1)-GED模型對應的AIC值為-12.858 2,顯著小于GARCH(1,1)-GED模型的AIC值-4.695 2。從整體上看, 24個模型中, 加入美元指數的m-PARCH(1,1)-GED模型的擬合優度最高, AIC值和SC值最小分別為-13.737 5和-13.718 8;其次是加入美元指數的m-GARCH(1,1)-GED模型, AIC值和SC值最小分別為-12.858 2和-12.844 0。GED分布下, 信息準則較優的兩個模型及其對照模型的參數估計結果見表5。

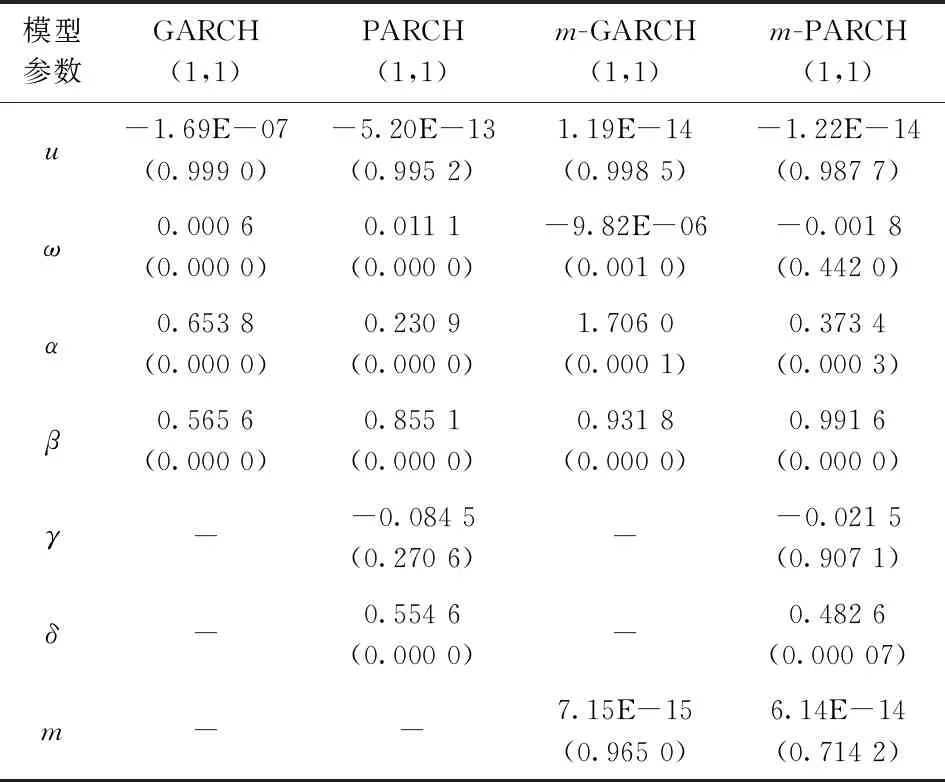
表5 GED分布假設下模型估計結果

其中， PARCH(1,1)模型和m-PARCH(1,1)模型中捕捉非對稱效應的參數γ對應p值為0.270 6和0.907 1均大于0.05, 參數不顯著, 說明人民幣匯率隔夜收益率數據不具有明顯的杠桿效應。權衡參數顯著性和擬合優度兩方面, 選用m-GARCH(1,1)-GED模型刻畫人民幣匯率隔夜風險的波動特征。m-GARCH(1,1)-GED模型中方差一階滯后項參數β對應p值為0, 參數顯著, 表明隔夜風險受滯后風險的影響。

提取出m-GARCH(1,1)-GED模型所擬合的標準差, 繪制成時序圖(圖4)。標準差的變化反映了人民幣匯率隔夜收益率的波動走勢。為檢驗異方差性是否消除, 對標準化殘差進行ARCH效應檢驗。結果顯示調整R2統計量為0.990 6, 其對應的p值為0.000 1, 表明ARCH效應基本消除, 證明了模型的有效性。

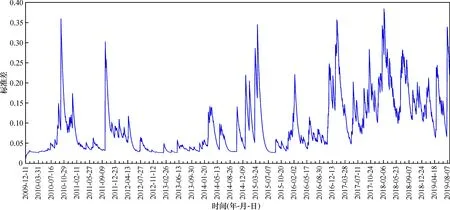
圖4 m-GARCH(1,1)-GED擬合的標準差的時序圖

將m-GARCH(1,1)-GED模型擬合得到的條件方差和標準差估計值代入式(13), 在0.05、 0.01兩個分位點下進行分位數回歸, 求解VaR值。將5%和1%顯著性水平下, QR-m-GARCH(1,1)-GED模型計算出的VaR與人民幣匯率隔夜收益率真實值r繪制在圖5中。可以看出, VaR值的動態走勢與人民幣匯率隔夜收益率波動走勢相近, 表明QR-m-GARCH(1,1)-GED模型能很好地刻畫人民幣匯率隔夜風險的每日動態變化。

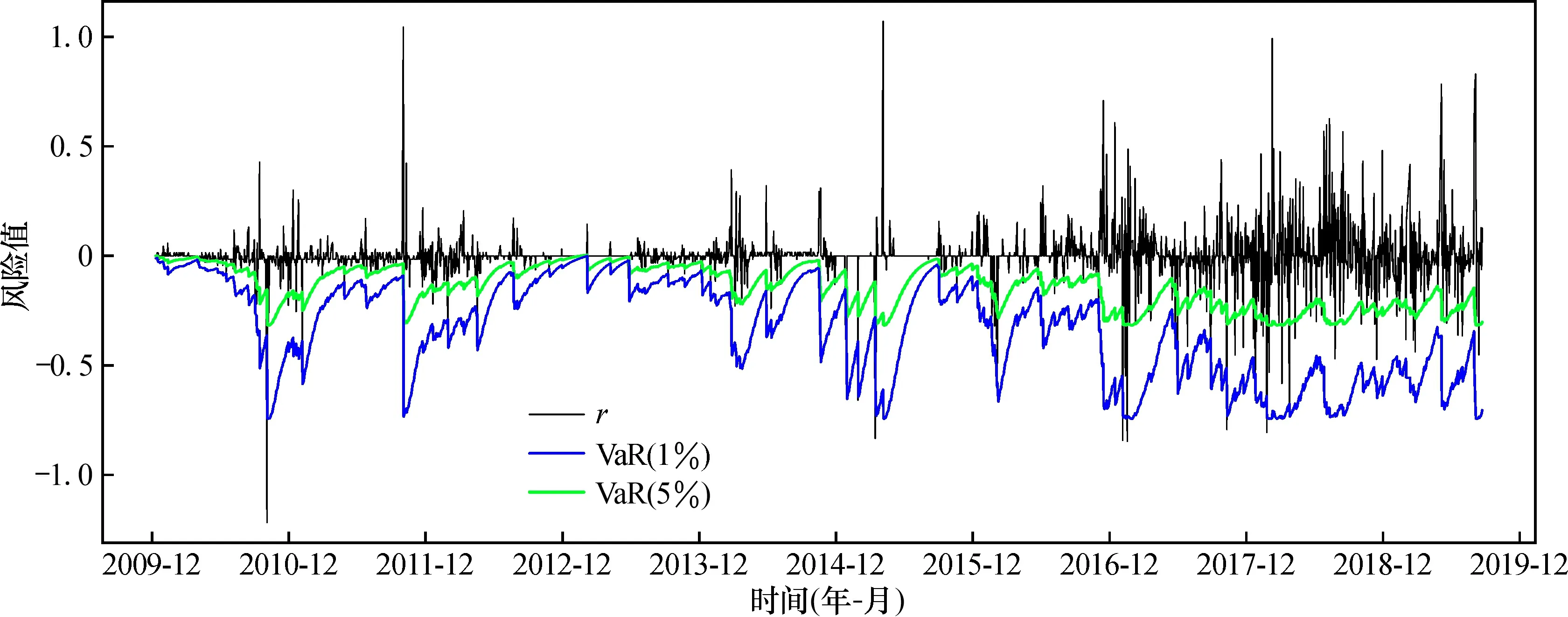
圖5 QR-m-GARCH(1,1)-GED模型風險預測圖

將QR-m-GARCH(1,1)-GED模型求解出的VaR值與人民幣匯率隔夜收益率真實值進行比較, 計算擬合成功率, 擬合成功率越高說明模型的擬合效果越好。同時與常數均值方程的QR-GARCH(1,1)-GED模型的結果進行比較, 結果見表6。

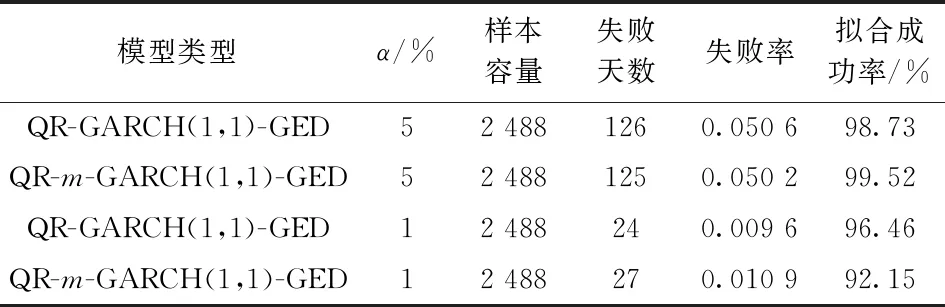
表6 擬合VaR成功率結果

在5%和1%顯著性水平下, 加入美元指數作為解釋變量的QR-m-GARCH(1,1)-GED模型對VaR的擬合成功率為99.52%和92.15%。QR-m-GARCH(1,1)-GED模型在5%的顯著性水平下的預測結果最接近理論值, 但在1%顯著性水平下擬合成功率不如QR-GARCH(1,1)-GED模型, 這表明QR-m-GARCH(1,1)-GED模型在高顯著性水平下更有優勢。5%的顯著性水平下, 均值方程中加入美元指數的QR-m-GARCH(1,1)-GED模型與QR-GARCH(1,1)-GED模型相比, 擬合成功率增加了0.79%， 這在一定程度上驗證了美元指數價格波動與人民幣匯率隔夜風險密切關聯。

3 結束語

由于中國和美國外匯交易市場開盤和收盤時間不同, 使得美元指數價格波動對人民幣匯率隔夜風險產生影響。本文在人民幣匯率隔夜風險的研究中, 加入美元指數作為人民幣匯率隔夜收益率序列的解釋變量, 建立QR-m-GARCH(1,1)-GED模型進行實證研究, 同時與常數均值方程的QR-GARCH(1,1)-GED模型進行對比。結果發現: 1)所選數據期間, 人民幣匯率隔夜風險的確存在, 并且匯率改革后波動明顯加劇； 2)人民幣匯率價格走勢存在被美元指數引導的現象； 3)人民幣匯率隔夜風險受滯后風險的影響； 4)相比QR-GARCH(1,1)-GED模型, 加入美元指數的QR-m-GARCH(1,1)-GED模型在高顯著性水平下擬合人民幣匯率隔夜風險更具優勢。

本文將美元指數作為人民幣匯率隔夜收益率的解釋變量, 區別于以往的常數均值方程, 更能體現我國外匯市場受美元指數價格波動的影響。使用QR-m-GARCH(1,1)-GED對人民幣匯率隔夜風險進行研究, 為央行和廣大投資者提供決策參考, 具有重要的理論和現實意義， 也為深入研究美元指數與人民幣匯率價格之間的關系提供了研究依據。