基于多元回歸模型和Topsis 模型對貨運線路價格的分析

張子璇 劉 鵬 楊洪滔 王會帆 崔思雯

（1、河北農業大學理學院，河北 保定071000 2、河北農業大學機電工程學院，河北 保定071000）

當今我國運輸市場開放，無車承運行業不斷發展。無車承運主要利用網絡平臺讓每個運輸任務被承運端司機接收，這需要提前將任務以一定的價格發布到互聯網上，司機瀏覽完后決定是否接收該運輸任務，如果任務未被接收，則需要調整價格來確保任務最終被接收，因此承運線路的科學定價問題也成為了無車承運人平臺亟待解決的問題。

1 實驗數據與處理方法

1.1 數據來源

本文所得數據來自我國無車承運人貨運線路歷史交易平臺。

1.2 所用軟件

SPSS、MATLAB。

1.3 數據處理

1.3.1 指標的篩選

為了選擇適當的模型，需要對數據進行預處理，首先確定研究的指標，我們查閱了影響貨運線路定價因素的相關資料后，確定了要研究的指標為：總里程數、線路編號、調價比例、始發網點、目的網點、交易成功時常、車輛長度、車輛噸位、線路總成本、業務類型、需求類型1、需求類型2、運輸等級、調價緊急程度、需求緊急程度。

1.3.2 數據分類

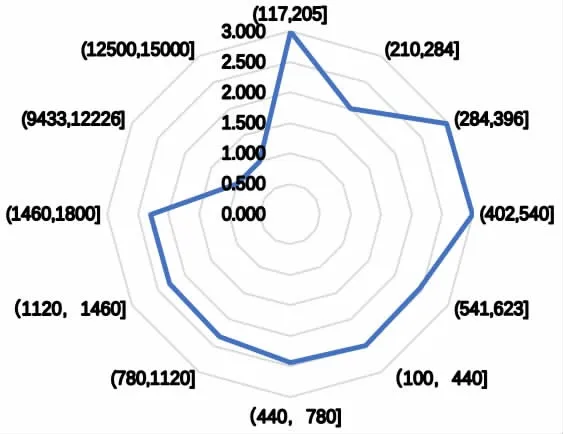
圖1 線路指導價格運輸能力圖

由于數據量太大，不易直接對其價格進行評價，所以我們對數據進行了分類，將線路指導價格分區間組合，共分為12 類，將其可視化如圖1 所示。

1.3.3 數據指標降維

為了便利實驗研究，本文利用因子分析降維。經計算得KMO 值為0.718＞0.5，可知原有因子適合進行因子分析。又經計算得累積方差貢獻率達到82.765%，故降維后的數據能夠代表絕大多數的初始數據。降維后的指標為線路價格、交易成功時長、調價緊急程度、線路成本、調價比例、車輛噸位、運輸等級。其中線路價格用y 表示，其他指標依次用X={x1x2x3…x6}表示。

2 模型的建立與求解

2.1 基于多元回歸模型的線路定價

2.1.1 計算步驟

Step1 線性模型假設

設X 與y 滿足如下線性關系：

Step2 聯合顯著性檢驗

對于多元線性回歸模型，在對每個回歸系數進行顯著性檢驗之前，應該對回歸模型的整體做顯著性檢驗。這就是聯合顯著性檢驗——F 檢驗[1]，假設：

選取F 統計量：F～F（k-1，T-k），我們得到聯合顯著性檢驗F（2，15）=16.008，P=0.0001＜0.01,所以在99%的水平下，拒絕原假設，即通過了聯合顯著性檢驗。

Step3 確定回歸方程

我們對回歸系數β1、β2…β6進行顯著性檢驗，假設：

2.1.2 實驗結果分析

利用上述回歸模型對未知的線路價格進行預測并初次定價，選用部分任務編號下的指標數據例如：

現將自變量取值分別帶入上文求得的回歸模型，我們可以預測得到每個任務編號對應的第一次報價，將其結果和已知實驗數據對比的預測效果比較好。

2.1.3 第二、三次調價策略

無車承運平臺市場復雜多變，假設每條線路最多只能發布三次價格，為了最大程度降低承運人的成本，建立運輸企業與貨主之間的長期供應鏈合作關系，需要我們對調價報價制定一個合理的策略。

（1）將第一次報價分為5 等級（級數越高，定價越高），其中總里程數小（≤100km）、業務類型為重貨、需求類型分別為普通和計劃、續簽狀態為已簽時，我們定義第一次報價等級為0 等級，有一個因素不滿足時，定價水平變為1 等級。

（2）對于第一次報價中未成交的任務，需要進行第一次調價處理，此次調價則以報價合理性為目標，在第一次報價策略的基礎上，每一等級相應的報價都是處于該等級的合理報價。

（3）若兩次報價都未成交，則以讓司機接受任務為目標，進行調價處理，此時每一等級相應的報價都是滿足司機要求的較高報價。

2.2 Topsis 模型對線路價格的評價

2.2.1 模型介紹

為了對線路指導價格進行評價，我們利用Topsis 優劣解距離法[2]對各個類別的價格進行評分，得分越高，則價格區間類別越好，從而確定最優類別價格、最劣類別價格和中間類別價格，并對其進行評價，分析其合理性。

2.2.2 計算步驟

Step1 指標分類

根據實際應用的可操作性，需對文中的七個指標分類，其中，線路價格、交易成功時長、調價緊急程度、線路成本為極小型指標，其他指標分類見表1：

表1 指標分類表

Step2 指標正向化

為了計算方便，需要將上述四種類型的指標正向化處理。

正向化處理的依據：

（1）極小型指標正向化公式：

Step3 標準化處理

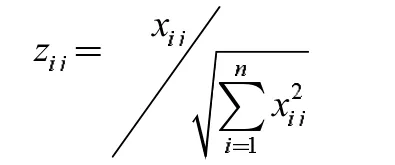
為了避免不同指標量綱的影響，需要對正向化的指標進行標準化處理。本題有12 個要評價的價格區間類別，7 個評價指標構成的正向化矩陣，正向化矩陣中的每一個元素用xij表示，記標準化的矩陣為Z,Z 中每一個元素的計算公式為：

Step4 計算得分并歸一化處理

在標準化后的指標中找到最優方案和最劣方案，然后分別計算評價對象與最優方案和最劣方案間的距離，獲得評價對象與最優方案的相對接近程度，作為評價優劣的依據，計算出價格的各個區間類別的最終得分，并對得分做歸一化處理：

2.2.3 實驗結果分析

將歸一化后得到的得分排序后可視化得到圖2，我們看到得分最低的價格類別是(9433，12226], 得分最高的價格類別是(210，284],得分處于中間的價格類別是(1460，1800]和(780,1120],并且我們得到除最后兩類價格，其他價格得分比較均勻，沒有太大的差異結論。基于實驗結果可以看出各分數段評分大體相同，由此我們認為：平臺定價較為合理，故其有一定的參考價值，在后續分析中我們可以以歷史數據的定價為基礎進行分析。

圖2 各段價格類別分數圖

3 結論

通過研究分析，我們發現無車承運人平臺的線路定價非常重要，對整個競爭市場的格局都產生著非常大的影響，所以，定價調價是具有挑戰性的決策。基于本文的回歸模型與實驗結果，結合我們制定的調價政策，能較為準確的預測出未完成訂單的報價。利用Topsis 模型對預測報價進行評價，發現不同區間之間評分較為均勻，合理性具有一定保證。由此評價結果也可以反應出我們的調價策略與預測結果較為合理，具有一定可行性。