利用雙參數地基模型修正反應位移法彈簧

邱滟佳,張鴻儒，于仲洋

(北京交通大學 土木建筑工程學院，北京 100044)

從20世紀70年代，日本學者提出反應位移法[1]以來，反應位移法由于理論嚴謹、模型簡單的特點逐漸成為實際工程中應用最廣泛的擬靜力方法之一，并且是國家規范[2-4]建議的方法之一，但是該方法也存在一定的缺陷.安軍海等[5]總結了反應位移法的幾個關鍵問題，其中非常重要的一個就是土彈簧剛度的確定方法.反應位移法采用部分近似條件將離散的地基彈簧模擬土層，計算結果存在一定誤差[6].已有研究表明，反應位移法在計算結構變形時誤差可達30%，計算結構內力時最大誤差接近40%[7].為了解決反應位移法計算誤差偏大的問題，大量學者對反應位移法進行了修正.董正方等[8]提出基于土層位移差的反應位移法，該方法適用于埋深較大地下結構；賓佳等[9]利用土-結構相互作用系數法的原理修正反應位移法，提出了基于變形修正的反應位移法，該方法能較好地提高反應位移法計算精度，但在計算中還需要考慮土-結構相互作用系數，會增加計算量.這兩種方法在一定程度上提高了反應位移法計算精度，但都沒有解決土彈簧剛度確定的問題.

為了忽略土彈簧計算帶來的誤差，部分學者提出通過直接建立土-結構分析模型來反映土-結構間相互作用.劉晶波等[10-13]提出的整體式反應位移法、整體強制反應位移法都是直接建立土-結構分析模型的計算方法.這一類方法計算精度明顯高于傳統反應位移法，但引入土單元會使簡單的反應位移法模型復雜化.

本文從另外一個思路出發修正反應位移法，用更接近土體性質的雙參數地基模型簡化土層，得到一種相比傳統反應位移法更加精確，又比整體式反應位移法、整體強制反應位移法模型更加簡單的地下結構抗震設計方法.

1 彈簧修正原理及修正方法計算過程

目前反應位移法已發展了多種計算形式，不同規范給出的計算模型也不相同，劉晶波等[14]以大開車站為案例，對比分析了不同規范中反應位移法的計算精度，結果表明《城市軌道交通結構抗震設計規范》[2]中的反應位移法模型更加合理.

規范[2]建議的反應位移法模型(見圖1)將地震對結構的作用分為3部分，即結構頂底及側墻剪力、結構慣性力以及側墻自由場變形.其中結構頂底剪力、結構慣性力、自由場變形均可由一維場地反應分析得到，側墻剪力取結構頂底剪力的均值[15]，同時反應位移法將周圍土體簡化成離散彈簧.丁德云等[16]總結并對比分析了離散彈簧的各種計算方法.將土體簡化成離散彈簧的方法雖然簡單，卻不能反映土體間的相互作用，影響結構的內力響應.

圖1 反應位移法示意

雙參數模型是一種能反映土體間作用的地基模型，本文利用雙參數地基模型原理對傳統反應位移法的土彈簧進行修正，以考慮土體間的相互作用.

1.1 雙參數模型及修正彈簧的原理

常見的雙參數模型有Filonenko-Boorodich模型、Hetenyi模型和Pasternak模型[17](見圖2).三者都用彈簧模擬土體的抗壓性質，這與溫克爾地基模型相同，但都增加了一個剪切參數來模擬土體之間的作用.3種模型本質是相同的，本文分析計算采用彈簧加剪切層的Pasternak模型.

圖2 雙參數模型

以結構底板為例，土體是摩擦性材料不受拉，可不考慮底板平面以上土層對底板彈簧的影響(見圖3模型A).傳統反應位移法將底板外土層簡化成離散彈簧，底板兩側彈簧不受力可直接去除(見圖3模型B、C),這樣的簡化方法會忽略底板兩側土體對結構的作用.采用Pasternak模型(見圖3模型D)，在剪切層的作用下底板兩側壓縮彈簧受力不能直接去除，能模擬兩側土體對結構的作用.

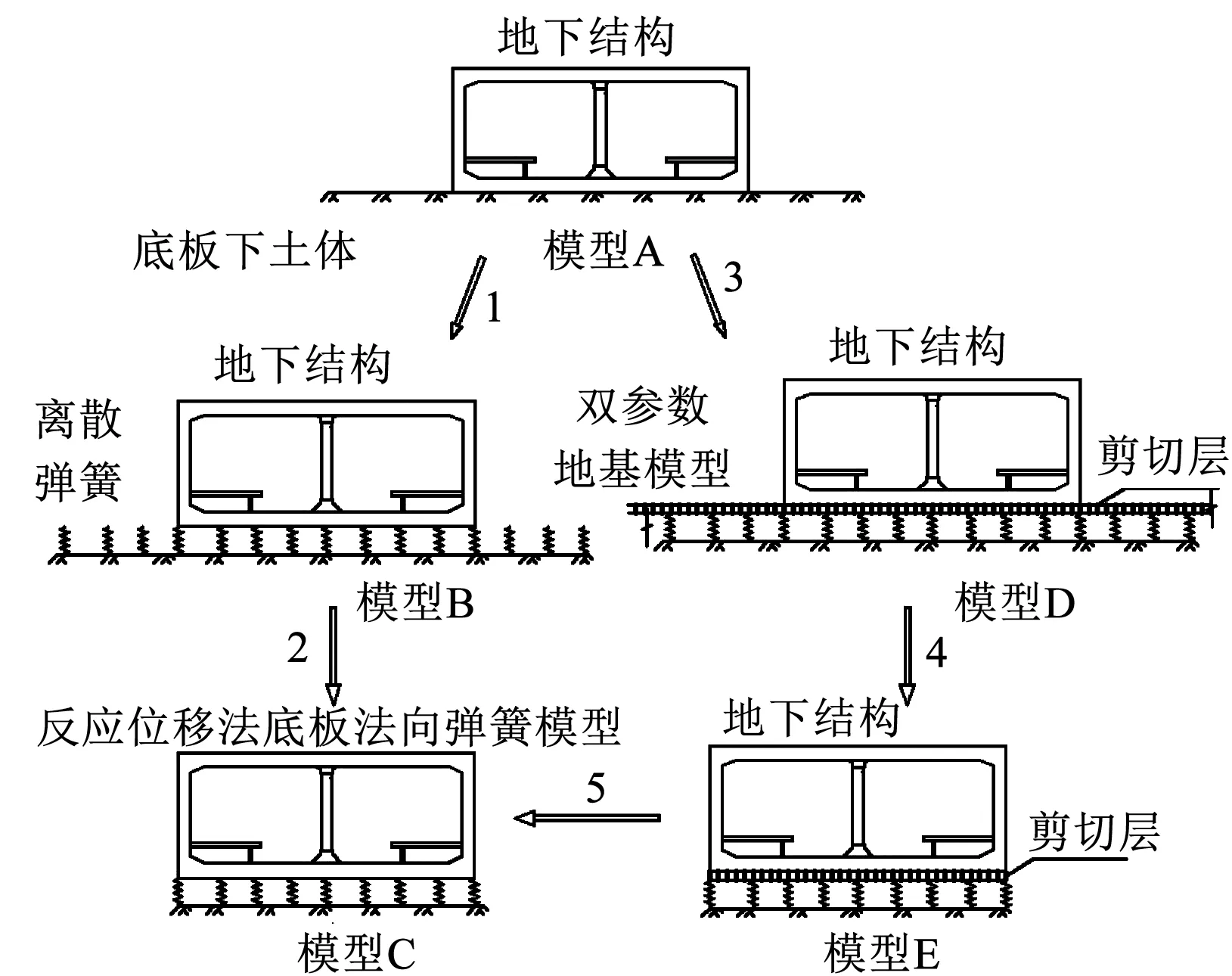
圖3 彈簧的簡化過程示意

為了簡化模型，經過分析可通過修正底板壓縮基床系數去除底板兩側的彈簧(見圖3模型E).以底板邊緣點處彈簧為例，修正原理如圖4所示，在同樣大小集中力F1、F2作用下，模型1結構底板位置的變形與簡化后的模型2相同.

張載[17]給出Pasternak模型在條形荷載作用下變形公式：

(1)

式中：w(y)為任意點變形；w0為力作用點下的變形；b為力的作用范圍，由于是集中力可取0；Ks為壓縮基床系數；Gs為剪切層剪切基床系數，當滿足最小勢能原理時，Gs=Ks.

圖4 雙參數模型簡化原理

模型1與模型2變形相同，則有模型1、2豎向反力F1、F2為

F1=Ks×B×l×w1+2×Ks×B×l×w2+…，

(2)

F2=K×B×l×w1+K×B×l×w2+….

(3)

式中：K為修正后的壓縮基床系數；l為壓縮彈簧的間隔；B為計算單元的寬度，二維模型取1 m.

由模型1、2豎向反力F1、F2相等得

(4)

當彈簧的間距l足夠小，上述求和公式就可以轉換成積分，得

式中L為模型2的寬度,即底板寬度.

利用同樣的方法得到其他位置的基床系數修正公式為

(6)

式中a為修正點到底板角點的距離.

由于結構底板的剪切剛度遠大于雙參數模型剪切層剪切剛度，在計算中可忽略底板下剪切層的作用，得到修正后底板外法向彈簧模型(見圖3模型C)，修正模型與傳統模型相比除了對彈簧系數進行了修正其他一樣.

1.2 雙參數模型的壓縮基床系數確定方法

從式(6)可以看出，修正基床系數K是雙參數模型壓縮基床系數Ks的函數，Ks的確定是修正模型非常重要的一步.其確定原理是在相同荷載作用下，采用不同的模型只會影響受力和變形的分布，不會改變地基土體整體的受力和變形.

目前，規范中有兩種離散地基彈簧的計算方法.其中更為精確且應用更廣泛的是有限元方法，本文Ks的確定方法就基于該方法.有限元計算離散地基彈簧基床系數Kl的公式為

(7)

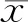
控制雙參數模型變形、受力與有限元計算結果相同，即

(8)

由式(7)和(8)得

(9)

式(9)為本文建議的雙參數模型壓縮基床系數Ks的計算公式，將其代入式(6)中就能得到反應位移法模型任意位置的修正基床系數.

1.3 修正反應位移法的計算過程

修正反應位移法計算過程與傳統反應位移法基本相同，分為3步：1)利用SHAKE91、EERA[18-19]等進行場地反應分析.得到結構位置處土層變形、剪力和加速度;2)求解模型的彈簧系數.模型的剪切彈簧直接利用規范中的有限元方法計算，法向彈簧利用本文的修正方法計算;3)建立模型并施加彈簧和地震荷載.其中頂、底板、側墻剪力以及結構慣性力的施加方法與傳統反應位移法相同.側墻的土層變形可直接施加在修正彈簧的遠離結構一側，也可轉化為由自由場變形乘以修正后彈簧系數得到的等效力.

2 修正反應位移法的驗證

地下結構抗震設計分析方法主要可分為動力時程分析方法和擬靜力分析方法(包含反應位移法)兩類，其中動力時程方法是在時域內直接計算地震反應過程中土-結構的動力相互作用的分析方法，其能夠計算地震反應過程中各時刻結構的內力和變形響應，計算精度高.為了驗證本文提出的修正方法計算精度高于傳統反應位移法，以動力時程的計算結果為基準對比兩種方法.

2.1 車站結構

以標準斷面為單層和雙層的車站結構驗證修正方法的正確性，其中單層車站為單層雙跨結構，車站寬度為12 m，高度為6.2 m；雙層車站為雙層三跨結構，寬度為20.3 m，高度為12.4 m，具體的構件尺寸見圖5.

圖5 計算模型的斷面(單位：m)

2.2 動力時程法

采用線性動力時程分析方法，單層結構模型計算尺寸為200 m×50 m(見圖6)，雙層結構模型計算尺寸為400 m×80 m.采用四節點平面應變減縮積分實體單元模擬土體介質，采用梁單元模擬結構構件.場地土與地鐵車站結構之間的法向接觸采用“硬”接觸的方式，即當場地土與地下結構之間出現拉力時，場地土與地下結構間的接觸面將立即分離；切向接觸服從Coulomb摩擦定律，當接觸面上剪應力大于它們之間的摩擦力時，將發生土體相對地下結構的切向滑動，計算過程中不同模型各個接觸面摩擦系數均取0.45.

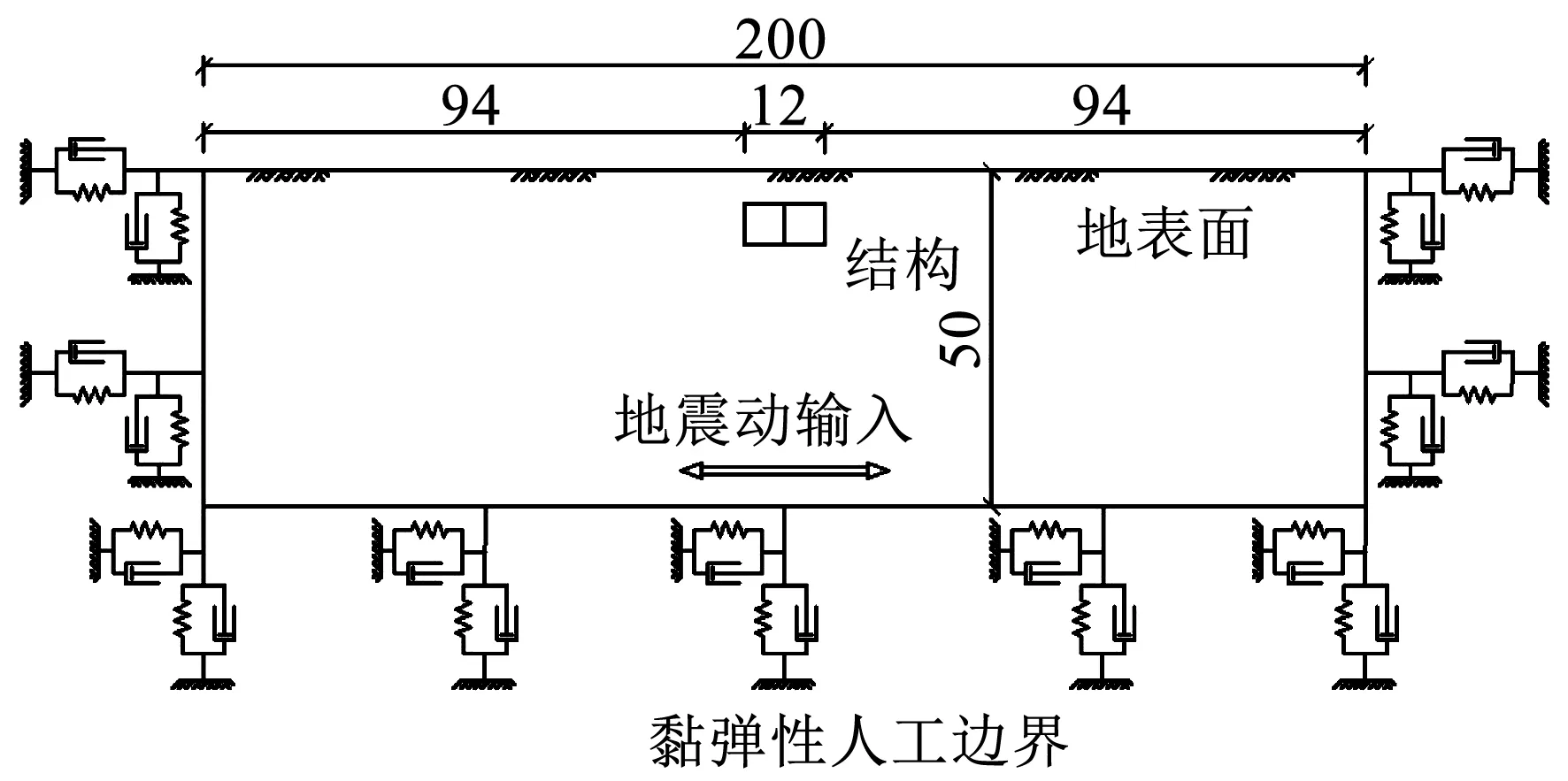
圖6 單層結構動力時程模型(單位：m)

場地土為單一飽和黏性土，并采用等效線性動力本構，即用黏彈性Kelvin模型來反映土體在周期荷載下的滯回性[20].剪切模量比、阻尼比和剪應變關系曲線如圖7所示.車站結構為C40混凝土，用彈性本構模擬.采用劉晶波等[21]提出的黏彈性動力人工邊界，該人工邊界是在模型邊界施加彈簧和阻尼系統以達到耗散和吸收散射波的目的，法向和切向彈簧阻尼參數計算公式為

法向邊界

(10)

切向邊界

(11)

式中：KBN與KBT分別為彈簧法向與切向剛度；R為波源至人工邊界點的距離；cs和cp分別為S波和P波波速；G為介質剪切模量；ρ為介質質量密度；αT與αN分別為切向與法向黏彈性人工邊界參數，取值如表1所示.

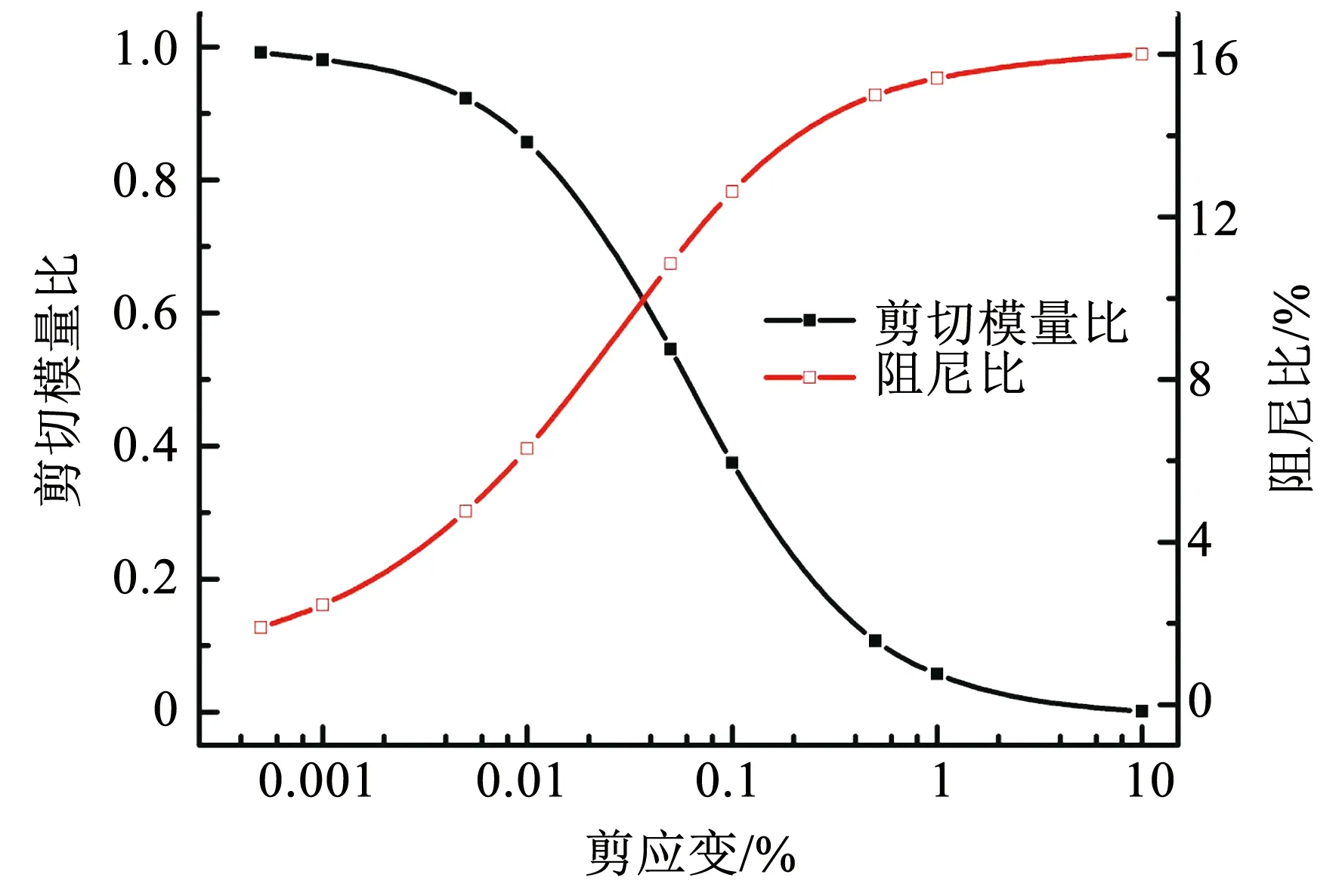
圖7 剪切模量比、阻尼比與剪應變關系

表1 黏彈性人工邊界參數取值

選用一個實際發生的地震波(El-Centro波)和一個人工合成波(北京人工波)作為地震輸入波分析不同地震輸入波對傳統方法及修正方法計算精度的影響.El-Centro波和北京人工波原始波形與頻譜分析見圖8，其中El-Centro頻譜曲線主要分布在低頻區，北京人工合成波分布較為均勻，兩者對比可分析輸入波的頻譜特性對修正方法計算精度的影響.

圖8 地震波原始波形和頻譜分析

2.3 反應位移法計算參數的獲取及計算工況

由于本文計算工況較多，不同工況下的反應位移法計算參數不同.以工況1為例計算傳統反應位移法和修正方法的參數，其他工況的參數用相同方法獲取.首先利用EERA進行場地反應分析，得到埋深2 m、地表峰值加速度為0.2g時，結構位置處土層變形、剪力和加速度，這一步修正方法與傳統反應位移法相同.然后利用有限元方法(見圖9)得到結構四周彈簧的基床系數，有限元的計算范圍與動力時程的計算范圍相同.

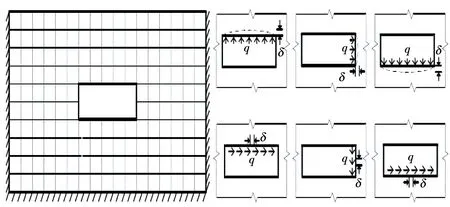
圖9 有限元方法計算基床系數

利用上述有限元方法得到的基床系數，是傳統反應位移法采用的基床系數Kl；根據式(9)得到雙參數模型壓縮基床系數Ks；最后利用式(6)得到修正模型任意點彈簧的修正基床系數K.工況1的傳統及修正基床系數見表2,其中a為彈簧位置到構件角點的距離.

表2 傳統及修正基床系數 kN·m-2

通過改變土體剪切波速、地震強度、結構埋深、結構層數和地震輸入波驗證修正方法在不同條件下的適用性和計算精度，具體的計算工況見表3.

2.4 計算結果及分析

本文計算工況較多， 由于篇幅的限制，只給出第一組工況的內力表(表4)，其他幾組工況的結果均以內力誤差圖的形式給出.

圖10～14給出各種工況下，以動力時程計算結果為基準，傳統反應位移法和本文修正方法的內力及變形誤差對比.綜合對比圖10～14可以得出，相比傳統反應位移法，修正方法的結果更加接近動力時程的計算結果，整體誤差能減小一半左右.

表3 計算工況

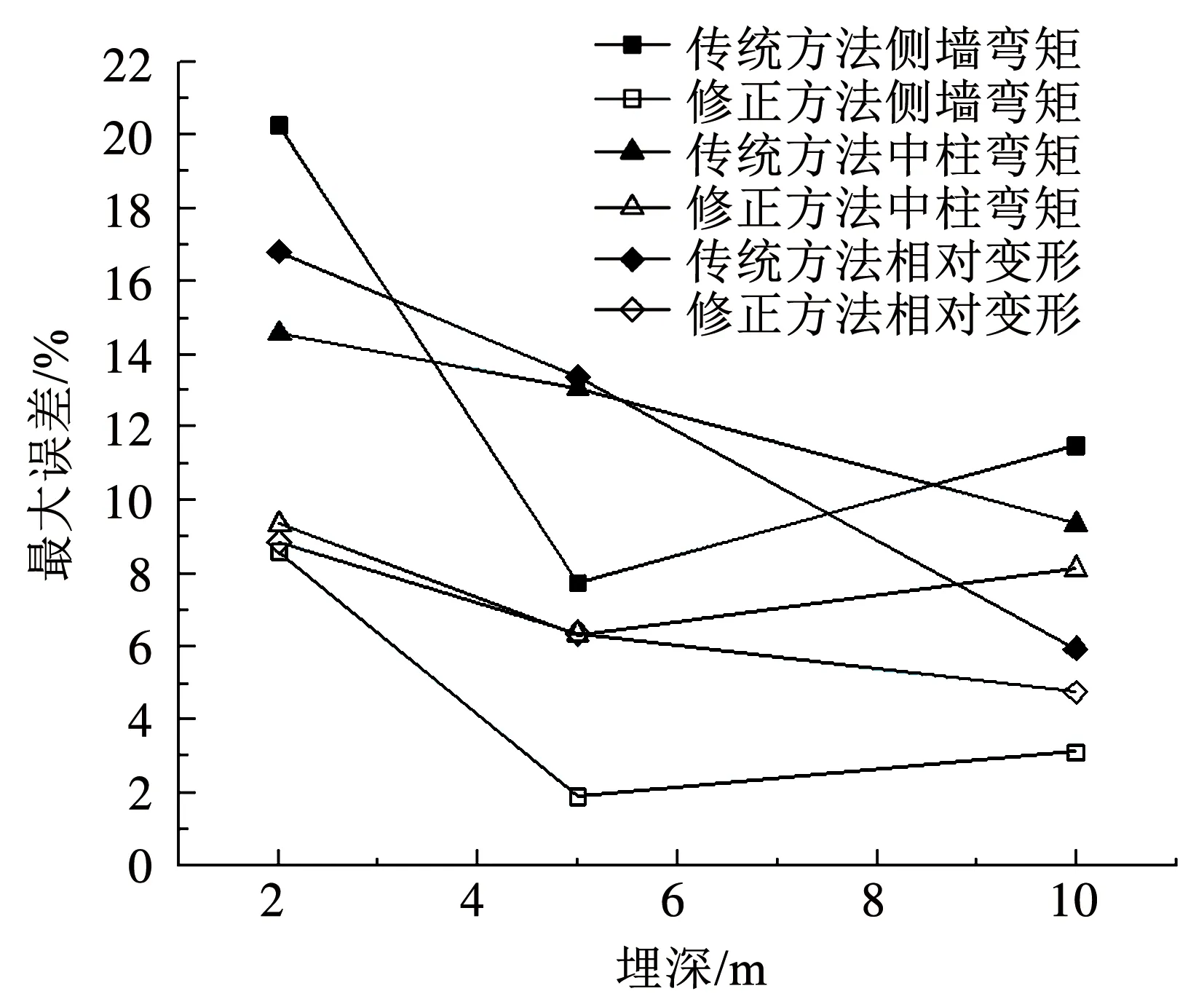
圖10 不同埋深傳統方法和修正方法誤差比較

圖11 不同土層剪切波速傳統方法和修正方法誤差比較

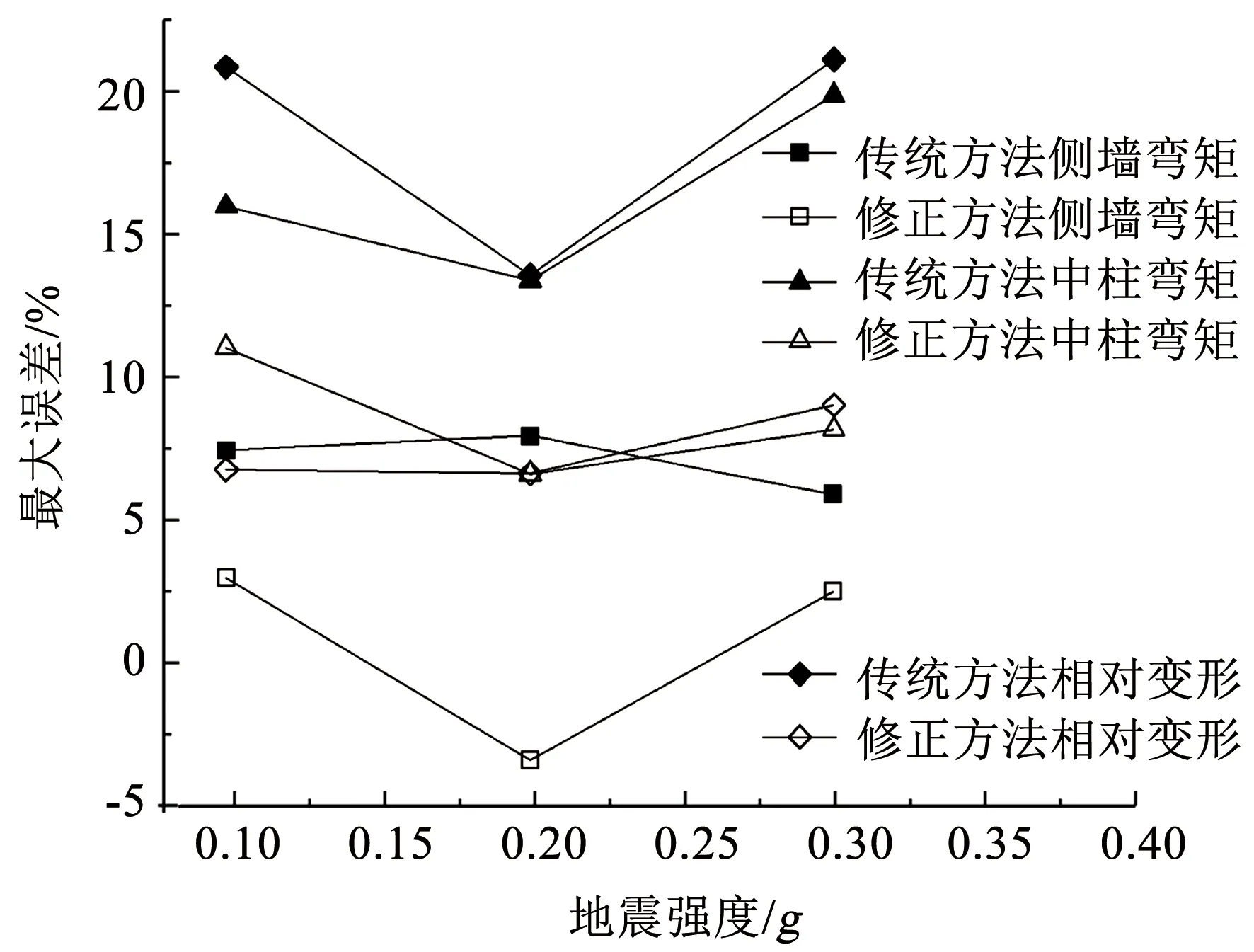
圖12 不同地震強度傳統方法和修正方法誤差比較

分別對比每種工況的結果可以得到，影響傳統反應位移法和修正方法計算精度的最主要因素是結構的類型.其中改變結構埋深、土層的剪切波速和地震強度(圖10～12)對兩種方法計算單層結構內力及變形精度的影響不大，傳統反應位移法內力及變形的最大誤差會達到20%，經過本文方法修正之后，內力及變形的最大誤差會減小到10%左右；改變結構類型(對比圖12,13)對兩種方法計算精度的影響明顯，其中用傳統反應位移法計算雙層結構的誤差是計算單層結構的2倍左右，修正方法計算雙層結構的誤差是計算單層結構的1.8倍左右；改變地震輸入波(對比圖13，14)對兩種方法的計算精度影響不大，傳統反應位移法最大計算誤差會達到40%，經過本文方法修正之后，最大計算誤差會減小到20%左右.綜合上面分析，修正方法的修正效果明顯.

圖13 雙層結構傳統方法和修正方法誤差比較

圖14 北京人工波為輸入波時傳統方法和修正方法誤差比較

3 結 論

1)修正方法除了修正法向彈簧的基床系數，其他部分與傳統反應位移法相同，仍然是一種相對簡單的地下結構抗震設計方法.

2)傳統反應位移法采用離散彈簧模擬土體，會影響結構內力響應，其計算精度偏低.對于單層結構傳統反應位移法計算誤差會超過20%；對于雙層結構其計算誤差則會超過40%.經本文提出的方法對彈簧進行修正之后，單、雙層結構的內力誤差都能減小一半左右，修正效果明顯.

3)修正方法是實用性較強且計算精度較高的地下結構抗震設計方法，可利用于地下結構的抗震設計中.

4)本文采用比傳統單參數模型更接近土體性質的雙參數模型簡化土層，但雙參數模型并不能完全模擬土體的性質，比如動力作用下土體剪切模量的非線性變化，所以，地基彈簧隨場地應力狀態的修正是進一步提高反應位移法精度的方向之一.