在“數據的離散程度”教學中感受統計實驗活動的樂趣

朱海忠

[摘? 要] 以“數據的離散程度”教學為例，創設有助于學生自主探究與合作交流的問題情境，構建統計實驗活動，引導學生積極思考、主動探索，讓學生在經歷統計實驗活動的過程中體會刻畫數據離散程度的意義，提煉方差的計算公式，領悟方差蘊含的統計思想，積累數學活動經驗，增強應用意識，培養數據分析觀念.

[關鍵詞] 統計實驗活動;極差;平均差;方差;標準差

《義務教育數學課程標準（2011年版）》（以下簡稱《課標（2011年版）》）將“數據分析觀念”作為數學課程的核心概念之一，要求學生對數據統計全過程有所體驗，強調發展學生的數據分析觀念. 《課標（2011年版）》在統計內容設置上，除了讓學生學習一些最基本的統計分析方法之外，更重要的是讓學生體會統計的作用和基本思想. 由于統計的學習特別強調學生對統計過程的參與性，要使學生真正理解統計的作用和基本思想，最有效的方法就是讓他們真正投入統計的過程中去. 只有在統計活動中，才能利用所學的統計知識和統計方法解決實際問題;只有熟悉統計活動的全過程，才能從整體上理解和把握所學的統計知識和其中蘊含的統計思想.

方差作為刻畫數據離中趨勢的統計量，它全面、平均地反映一組數據與其平均數的偏離程度，是現代統計學中最常用的統計量之一. 《課標（2011年版）》要求“體會刻畫數據離散程度的意義，會計算簡單數據的方差，知道可以通過樣本方差推斷總體方差，能解釋統計結果，根據結果做出簡單的判斷和預測，并能夠進行交流”[1]. 本文以北師大版八年級數學下冊第六章第4節“數據的離散程度”（第1課時）為例，創設有助于學生自主探究與合作交流的問題情境，構建統計實驗活動，讓學生在經歷統計實驗活動的過程中體會刻畫數據離散程度的意義，提煉方差的計算公式，領悟方差蘊含的統計思想，積累數學活動經驗，增強應用意識，培養數據分析觀念.

創設情境，溫故知新

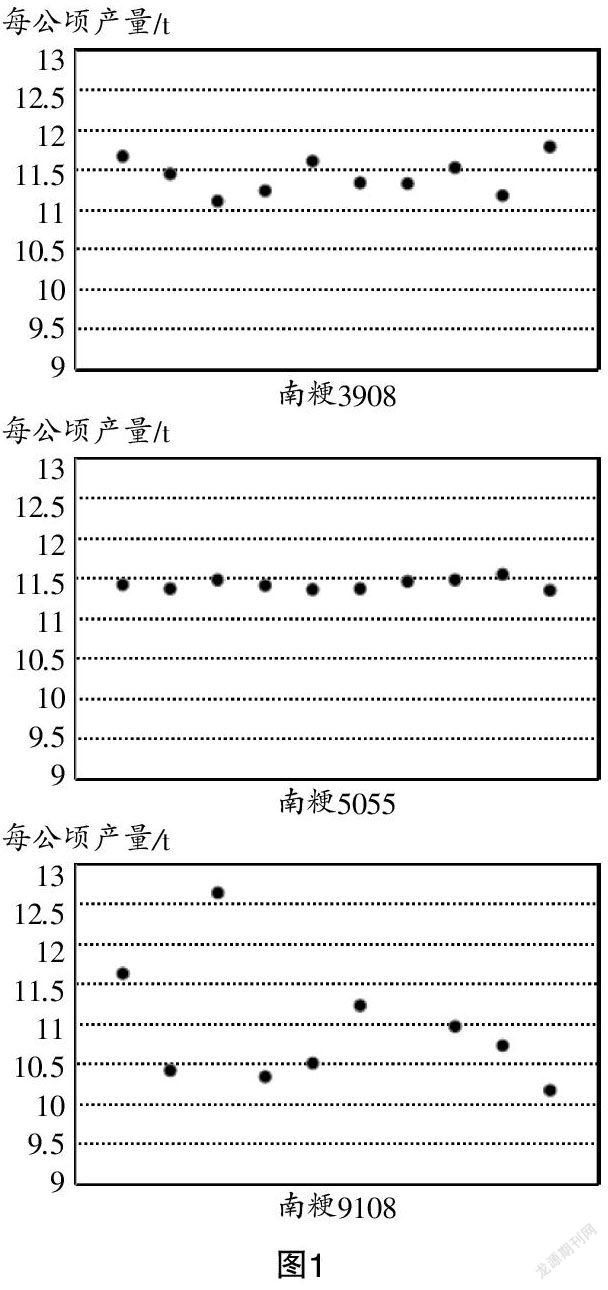
案例1 某農科院計劃為某地篩選出適應性好、綜合性狀優、產量潛力大且產量穩定的水稻新品種. 為了解“南粳3908”“南粳5055”“南粳9108”三種水稻新品種的相關情況，農科院各用10塊自然條件相同的試驗田進行比較試驗，得到各試驗田每公頃的產量（單位：t）如表1所示[2].

根據這些數據估計，你認為農科院應該選擇哪一種水稻品種？

探究活動1：如何比較三種水稻的產量水平？

（1）你能結合表1的數據直接估計出三種水稻每公頃的平均產量嗎？請你先估計，再計算三種水稻每公頃的平均產量，并與你的估計進行比較（結果保留3位小數）.

（2）根據三種水稻每公頃的平均產量，你認為農科院應該選擇哪一種水稻品種？為什么？

（3）除了比較三種水稻每公頃的平均產量外，還可以從哪些方面對三種水稻每公頃的產量水平進行比較？

（4）表1中南粳3908每公頃的產量最大值是多少？最小值又是多少？它們相差多少？南粳5055和南粳9108呢？

（5）一組數據的極差有什么特點，它能反映這組數據的整體離散情況嗎？是否還有其他的數學量可以刻畫數據的波動情況呢？

設計意圖 案例1力圖讓學生經歷解決一個統計問題的全過程，激活學生用數據說話的意識，讓其通過數據分析做出判斷，解決實際問題，體會數據中蘊含的信息. 探究活動1意在引導學生從數據集中趨勢的角度分析數據. 問題（1）旨在讓學生直觀估計三種水稻的平均產量，然后通過具體計算評判自己的估計水平，調整自己的估計;問題（2）（3）意在讓學生發現南粳3908與南粳5055的平均產量最高，且相同，僅靠比較二者的平均產量還無法做出判斷，讓學生意識到僅考查數據的集中趨勢是不夠的，還需要從數據離散程度的角度進行考查，從而借助問題（4）引入刻畫離散程度的一個量——極差;問題（5）旨在讓學生明確極差是一組數據中最大值與最小值的差值，它可以描述一組數據的波動范圍，但它僅反映了這組數據中兩個極端值的離散程度，沒有充分利用整組數據信息，不能反映這批數據離散的整體情況，還需尋找其他的數學量精確刻畫數據的整體離散程度.

建構活動，領悟意義

探究活動2：考查一組數據的離散程度需要有一個比較標準，用什么量作為比較標準比較合適？如何與這個標準進行比較呢？[3]請你思考如下問題.

（1）把表1的數據表示成如圖1所示的散點圖. 觀察圖1，三種水稻每公頃的產量分布有什么特點？

（2）在圖1中畫出縱坐標等于平均數的直線，觀察數據的分布與其平均數所在的直線之間的位置關系，你有什么發現？

（3）如何量化單個數據相對其平均數的偏離程度？又如何量化整組數據相對其平均數的偏離程度？

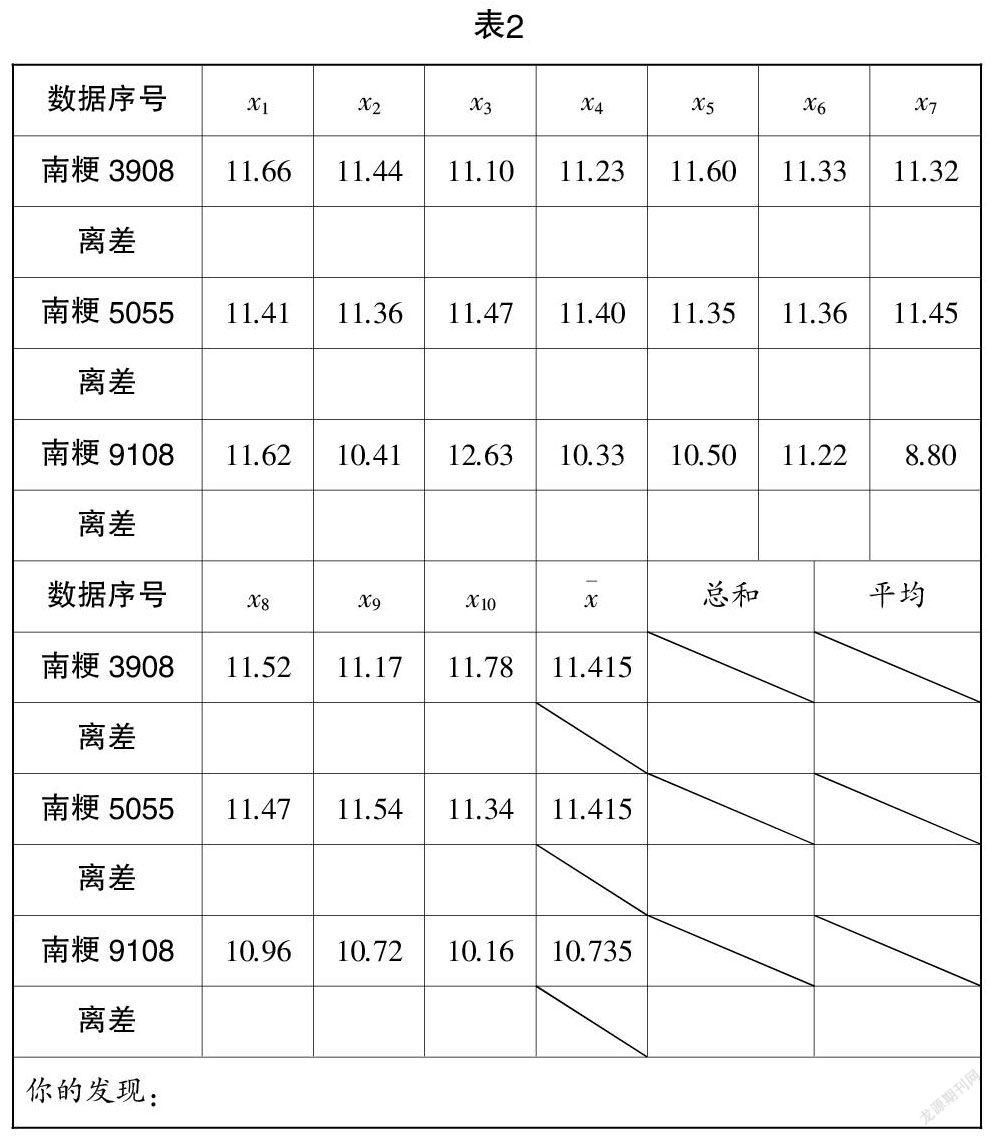
實驗活動1：發放表2，指導學生利用Excel軟件或者計算器，合作完成表2的探究內容（結果保留3位小數）.

（4）如何對“離差”進行數學處理以避免出現正負相消的情況？你有哪些方案？

實驗活動2：發放表3和表4，指導學生利用Excel軟件或者計算器，合作完成表3和表4的探究內容（結果保留3位小數）.

設計意圖 探究活動2意在讓學生經歷利用“平均差”和方差刻畫數據離散程度的過程，讓學生意識到要刻畫數據的離散程度首先要找到一個可以進行比較的參照對象. 為此，設置問題（1）讓學生直觀分析數據的離散程度，再通過問題（2）引導學生發現三種水稻每公頃的產量均集中分布在各自的平均產量附近，且圍繞其平均產量上下波動. 從而讓學生意識到，刻畫數據的離散程度的比照對象就是這批數據最集中的位置，即反映數據集中趨勢的平均數;問題（3）意在引導學生發現并采用“離差”（數據與其平均數的差）來量化單個數據相對其平均數的偏離程度，通過將這些“離差”求和或求平均數的方式來量化整組數據相對其平均數的偏離程度. 然而通過實驗活動1，學生自然會發現，這些“離差”的總和為0，從而導致這批數據的離散程度由于這批“離差”中的正負抵消而不能真正刻畫數據的離散程度. 為此，通過問題（4）繼續引發學生思考，讓學生在討論與交流中得出兩種常見的數學處理方式——對“離差”作絕對值或平方. 通過實驗活動2完成三種水稻每公頃的產量的離散程度的量化，為后續生成“平均差”和方差（標準差）的概念做好鋪墊.

模型歸納，生成概念

1. 模型歸納，醞釀概念？搖

師生共同回顧刻畫數據離散程度的過程（見圖2），總結計算“平均差”和方差的基本步驟[4].

2. 語言轉化，生成概念？搖

3. 對比分析，了解優劣

問題：通過實驗活動2，我們分別計算出三種水稻每公頃產量的“平均差”和方差（表5），如果利用“平均差”和方差分析三種水稻每公頃產量的波動狀況，你能得出什么結論？

探究活動3：觀察南粳9108每公頃產量的“平均差”和方差的計算演示過程，你能結合加權平均數的知識進行分析嗎？談談你的發現.

4. 概念延伸，回歸精確

問題：通過探究活動3，我們發現在實際應用中，用方差來描述數據的離散程度時，由于計算中進行了平方，從而可能放大該組數據離散的程度，并且其單位與原來數據的單位不一致，你能繼續改進這個量嗎？

設計意圖 首先通過模型歸納，由特殊到一般，引導學生歸納小結求一組數據的平均差和方差的一般步驟與計算公式. 通過對比分析，引導學生發現，“平均差”或方差越大，數據的波動越大;“平均差”或方差越小，數據的波動越小. 通過探究活動3繼續引導學生發現，“平均差”是離差的簡單算術平均數，離差的大小并不影響其權重，所以對于“平均差”來說，極端數據的變異性被同等看待了. 而方差則可以看成是以離差本身大小為權重的加權平均數，所以越極端的數據會被給予越多的關注，這一點也更符合人們對于數據變異性的直接感[5]，因此，采用方差就比較有效地衡量出這種變異性. 最后通過概念延伸，引出標準差s的概念，即s=. 讓學生明確標準差既能從量上反映這批數據的離散程度，又能使單位與實際相一致，同時也避免方差由于平方后可能夸大離散的程度.

案例研習，運用概念

1. 典例示范，提升學力

案例2 2019年10月1日上午10時，北京天安門廣場隆重舉行慶祝中華人民共和國成立70周年閱兵式活動. 寬闊的長安街上，大軍列陣，鐵甲生輝. 巍峨的天安門前，旌旗飄揚，舉世矚目. 這是中國特色社會主義進入新時代的首次國慶閱兵，也是共和國武裝力量改革重塑后的首次整體亮相. 古老滄桑的中華民族，久經風雨的偉大祖國，在這場舉世關注的閱兵盛典中煥發出勝利與自豪的榮光（播放國慶70周年閱兵分列式視頻片段，約2分鐘）.

我們知道接受檢閱的儀仗隊必須精挑細選，整齊劃一，特別注重隊員的身高，表6是從甲、乙兩支儀仗隊隊員中隨機選取的10名隊員的身高（單位：cm），哪支儀仗隊隊員的身高更為整齊？你是怎么判斷的？

探究活動4：當樣本數據較大時，方差的計算較為繁復，你有什么方法可以簡化計算嗎？

（1）如果以185（cm）為基準，將甲、乙兩組數據都減去185后再計算兩組新數據的方差會有什么結果？你有什么發現？

實驗活動3：發放表7，讓學生利用Excel軟件或者計算器，合作完成表7的探究內容（結果保留2位小數）.

（2）你能利用完全平方公式和離差的性質（數據離差的代數和為0），化簡方差的計算公式嗎？

2. 公式應用，內化新知

案例3 某單位要買一批直徑為60 mm的螺絲.現有甲、乙兩個螺絲加工廠，它們生產的螺絲的材料相同，價格也相同. 該單位分別從甲、乙兩廠的產品中抽樣調查了20個螺絲，它們的直徑（單位：mm）如下：

甲廠：60，59，59.8，59.7，60.2，60.3，61，60，60，60.5，59.5， 60.3，60.1，60.2，60，59.9，59.7，59.8，60，60;

乙廠：60.1，60，60，60.2，59.9，60.1，59.7，59.9，60，60，60， 60.1，60.5，60.4，60，59.6，59.5，59.9，60.1，60.

你認為該單位應買哪個廠的螺絲？[6]

設計意圖 案例2旨在讓學生重溫國慶70周年閱兵分列式的震撼場面，切身感受到祖國的強大和繁榮，增強學生的民族自豪感，培養愛國主義情懷. 構建探究活動4引發學生深入思考，通過簡化方差的計算公式，引導學生經歷處理數學問題的過程，提升學生形式化的推理能力，激發學生學習統計和數學的興趣. 案例3則意在讓學生進一步熟練應用平均數、方差（標準差）解決實際問題，體會二者的統計意義，明確在實際應用中，對不同組別的數據進行比較選擇時，當各組數據的差異較大時，應當首先考慮平均數的作用;當各組數據的平均數相等或者很接近時，要結合數據的離散程度進行分析，根據離散程度來進行選擇.

梳理小結，歸納提升

問題：（1）本節課你學習了哪些知識？你能刻畫“成績更穩定”這種直觀判斷嗎？

（2）極差、平均差和方差（標準差）有什么作用？

（3）怎樣合理利用方差（標準差）解決實際生活中的問題？

設計意圖 引導學生回顧極差、平均差和方差（標準差）等相關知識的產生和獲得過程，構建知識結構框圖（圖3）[7]，培養學生歸納和總結知識的能力，重點在回顧方差的概念生成過程和理解方差（標準差）的統計意義上.

結束語

本文通過創設有助于學生自主探究與合作交流的問題情境，構建有效的統計實驗活動，使學生經歷完整的統計過程，包括收集數據、整理數據、展示數據、從數據中提取信息，并利用這些信息說明問題. 本文旨在讓學生在這樣的過程中，不斷積累統計經驗，加深理解統計思想與方法，使統計學的教學散發出它原本應有的活力與樂趣，增強中學生對統計學的學習興趣與能力.

參考文獻：

[1] 中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2012.

[2] 張鵬，王中德，周寶紅，步學林，王君，溫凱. 水稻品種比較試驗[J]. 現代農業科技，2020（21）.

[3] 萬榮慶. 清晰認識概念 理解數學本質——對“方差”概念的分析與思考[J]. 復印報刊資料：中學數學教與學， 2009（06）.

[4] 王華. 關注概念形成 激活學生思維——“方差與標準差”概念形成過程的兩次教學設計[J].中國數學教育，2014（05）.

[5] 梅林晨. 對于平均差與標準差的數學關系和應用價值比較研究[J]. 赤峰學院學報（自然科學版），2015，31（15）.

[6] 馬復. 義務教育教科書·數學（八年級上冊）[M].北京：北京師范大學出版社，2012.

[7] 封小波. 構建統計實驗活動 樹立數據分析觀念——以“平均數”教學為例[J]. 中學數學教學參考，2020（29）.