一種OFDM信號多參數估計識別改進方法*

張 曄，吉 磊，熊 剛

（中國電子科技集團公司第三十研究所，四川 成都 610041）

0 引言

隨著通信技術的迅猛發展，電磁空間環境日益復雜，頻譜資源更加緊張。正交頻分復用（Orthogonal Frequency Division Multiplexing，OFDM）信號由于具有頻譜利用率高、抗多徑能力好、可有效抑制符號間干擾以及分配信道資源靈活等優點，已經在民用和軍事通信系統被廣泛采用[1-2]，如數字音視頻廣播業務系統、無線局域網系統、4G 移動通信系統、無人機測控通信系統和美國陸軍戰術作戰人員信息網（Warfighter Information Network-Tactical，WIN-T）等，且被運用于新一代無線網絡通信標準。此外，信號處理及分析技術的研究也受到了眾多學者和機構的關注。在非協作通信情況下，對參數的估計識別是實現后續解析的前提，能更好地提取到有用參數信息。OFDM 信號具有多種重要參數，包括循環前綴（Cyclic Prefix）長度、載波頻偏、定時誤差和過采樣因子等。通過估計算法獲得這些OFDM 參數，可為實現同步、均衡和解調等提供依據。

對OFDM 信號的參數估計識別方法一般包括有預處理、特征提取與參數計算估計等步驟。其中，預處理主要是對采集的信號樣本進行正交下變頻、濾波和平滑等；特征提取是指在時域、頻域或其他一些變換后分析OFDM 信號性質，可提取出多種有用特征量，從而實現對信號參數的計算估計。一些研究人員和學者對OFDM 信號的參數估計識別開展了研究。其中：Ishii 和Wornell 提出了一種參數估計算法，主要通過OFDM 信號幀中的大量符號累積實現計算，且需要導頻等先驗信息[3]；文獻[3-4]是在已知采樣頻率的假設下，采用相關法來研究OFDM 系統的系統參數，其中文獻[4]提出的方法在符號定時未同步的情況下性能并不理想。

針對上述問題，本文在信號循環平穩性分析的基礎上，提出了一種基于循環譜的OFDM 信號參數識別改進思路，抗噪性較強，利于工程實現。該方法通過構建OFDM 信號循環平穩特性分析對應的計算模型，準確提取了包括OFDM 循環前綴長度、子載波數目、過采樣率、載波頻率以及定時偏差等多個重要參數，在對子載波識別運算過程中利用循環相關性實現了優化處理，并進行OFDM 信號的循環前綴與時頻域特征融合分析，提高了算法在低信噪比條件下的穩健性能。

1 循環平穩特性分析計算模型

圖1 表示了OFDM 信號的基本傳輸原理。將信號發送端的串行數據流經過串-并轉化變為并行數據，然后把對應于各子載波上的數據符號分別進行星座映射調制后再進行傅里葉逆變換IFFT，并加上循環前綴（Cyclic Prefix，CP）形成OFDM 調制信號。對于接收方，把收到的OFDM 信號進行去循環前綴、同步解調以及并-串轉換等處理，還原為比特流信息數據。

圖1 OFDM 信號傳輸原理

信號x(t)的二階循環平穩特性可以利用時變相關函數式表示：

式中，R(·)表示相關函數，E(·)表示數學期望，t表示周期性時間變量，τ表示時延。

設M為信號數據長度，在循環頻率α位置處的循環自相關函數即為Cxx(α,τ)。它實質上是Rxx(t,τ)關于時間t的傅里葉級數，數學表達式為：

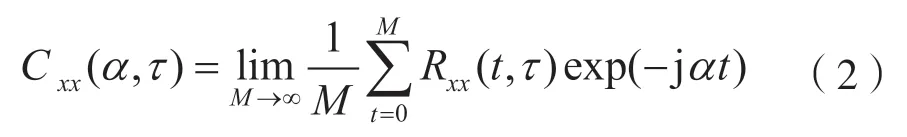
對于OFDM 信號，設x(t)表示接收機收到的信號。經過采樣，下變頻和濾波處理后可表示為：

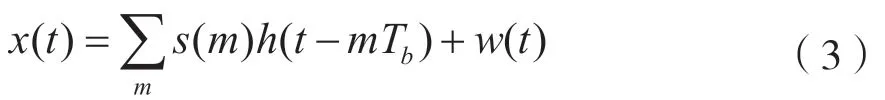
式中：s(m)表示循環前綴為CP 的OFDM 基帶信號；Tb表示信號在時域上每個采樣點的持續時間長度，即采樣時間間隔；h(t)表示系統傳輸函數，主要由接收濾波器響應和信道衰落函數組成；w(t)表示方差為的加性高斯白噪聲。

為簡化推導過程，可假設基帶傳輸信號包絡為矩形脈沖且信道為高斯信道。設過采樣因子可表示成q取為足夠大的數值，Tb和分別為變換前后的采樣間隔。已接收到的采樣信號序列x(n)是通過采樣頻率為的過采樣接收信號得到的，即：

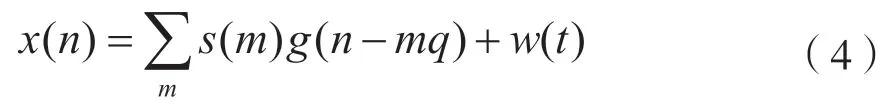
式中，s(m)表示信號序列，可歸一化為1，g(l)為矩形脈沖，可表示為：

當q為整數時，在τ=11處的離散時變相關函數Rxx(n,τ)是周期函數，周期為q；當q為分數時，Rxx(n,τ)是近似周期函數。于是，有：

式中，l為大于1 的任意整數。接收到的信號經過采樣后轉換為離散序列，因此可使用離散數據表示時間延遲。當q為整數時，OFDM 信號序列與噪聲是相互獨立的，信號功率為，Rxx(n,τ)是一個矩形脈沖序列，可表示為：

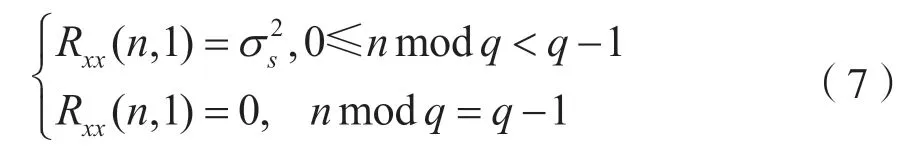
因為式（7）是一個以q為周期的函數，所以當延遲q＞τ=1 時，離散時變相關函數Rxx(n,τ)即為一個周期為q的函數。

實際中由于引入了循環前綴CP，OFDM 信號具有循環周期性。OFDM 信號時變相關函數s(m)包絡為周期性的矩形脈沖，其周期Tall=Ts+Tcp，其中Tcp=GTb代表循環前綴CP 的持續時間，G表示循環前綴的長度，且有Ts=NTb表示OFDM 有用符號的持續時間。

2 估計識別算法分析和改進

2.1 基于循環譜的參數估計識別思路

若OFDM 信號以α為循環頻率，時延為τ，其對參數的估計識別數學表達式為：

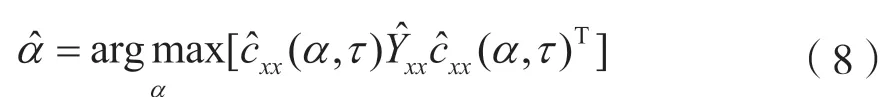
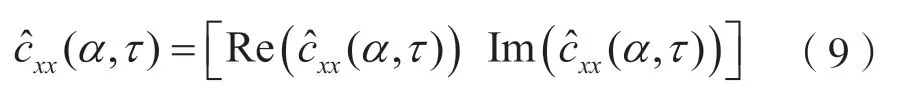
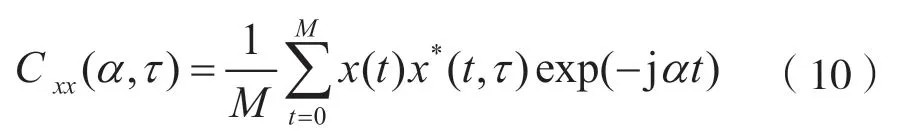
2.1.1 OFDM 過采樣因子估計識別

OFDM 參數識別的第一步是提取出OFDM 過采樣因子特征。對于OFDM 信號，一般都采用高采樣頻率生成波形，導致有效符號長度中含有的采樣點數量大于其子載波數量即OFDM 調制解調時IFFT/FFT 點數，原因是相比帶寬使用了比最小不失真采樣率更大的采樣率，由此引入了過采樣因子參數。

過采樣因子的大小由接收機和發射機使用的采樣頻率之間的比值決定。在OFDM 信號接收機端進行FFT 處理前，須使得有效符號長度內采樣點數目和子載波數目相等。對過采樣因子參數識別的作用是為了消除OFDM 解調過程中由于過采樣帶來的影響。

當τ＜q時，接收到的過采樣OFDM 信號具有循環平穩特性。設τ=1，時延τ是固定值，在循環頻率α處的是一個復數隨機過程。

過采樣因子可表示為：

通過采用循環譜變換進行分析，式（11）還可表示為：

式中，P表示FFT 長度，表示循環譜頻率的峰值之間對應的距離。

2.1.2 OFDM 子載波數量估計識別

OFDM 子載波數量是OFDM 重要的時域參數之一[5]，傳統方法是通過對OFDM 信號帶寬Bw和有用符號持續時間分別進行估計計算[6]，再采用式（13）求得結果[7]。對OFDM 有用符號持續時間的計算思路可結合前述的過采樣因子，然后得到子載波數目：

為簡化運算，這里采取一種基于循環譜的改進思路實現子載波數目的估計識別。

根據OFDM 信號的循環平穩特性，若對信號的時變自相關函數Rxx(n,τ)作FFT 變換，將出現離散的譜線峰值。如果譜線峰值間距離為D，FFT 點數是M，則可得周期q=M/D。根據對Rxx(n,τ)在FFT變換后峰值譜線間距離的搜索計算，可求出過采樣率，然后進一步估計出OFDM 信號的有效符號長度，即：

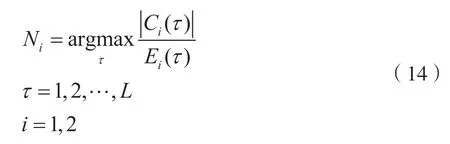
式中：

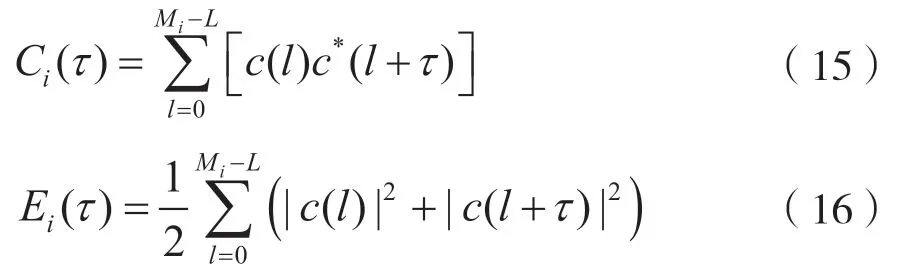
L表示偏移長度量的最大值，Ci(τ)表示相關函數值（τ∈[1,L]），Ei(τ)表示信號能量均值，Mi表示對參數估計的數目。計算有效的條件是偏移長度量需要大于有效符號長度。

OFDM 信號子載波數目為：

2.2 多參數聯合估計識別思路分析

基于循環譜分析算法可實現對OFDM 信號多參數的識別，包括循環前綴長度、載波頻偏以及定時誤差等。

因為OFDM 信號是具有循環平穩性的信號，所以可將τ=Ts代入式（8）來估計識別相應的循環頻率或符號持續時間，并可得出：

傳統的OFDM 參數估計器是通過FFT 變換后的序列系數計算來進一步求取結果[8]，且需要大量的采樣樣本點數以提高精度[9-10]。本文根據循環平穩統計量得到了對頻率偏移和定時誤差等參數的聯合估計識別改進方法。

首先對信號進行降采樣，設信號的頻率偏移為v，定時誤差為ε，OFDM 信號可表示為：

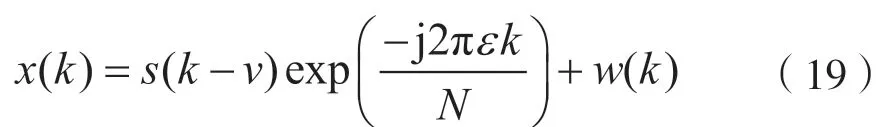
由于OFDM 信號中CP 具有相關性，因此對OFDM 有用符號持續時間Ts的估計器可以表示為：

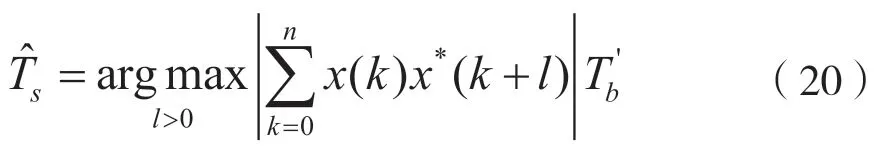
其次，將式（19）代入式（20），其中的相關部分對應為循環頻率為0 時的循環譜值。由于引入了CP，在τ=N時，相關部分轉化為：

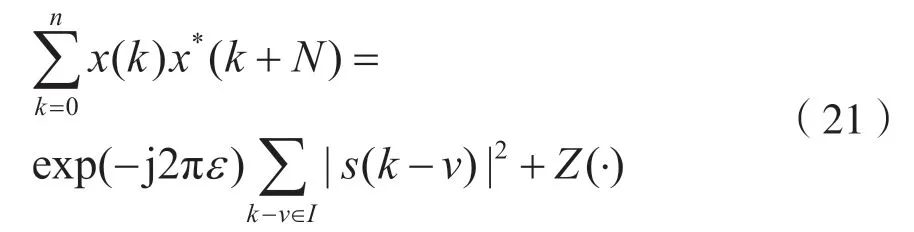
式中，I表示CP 中k值的集合，且有：

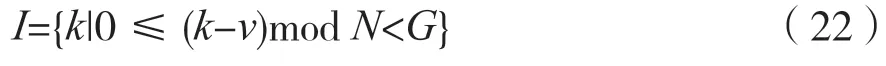
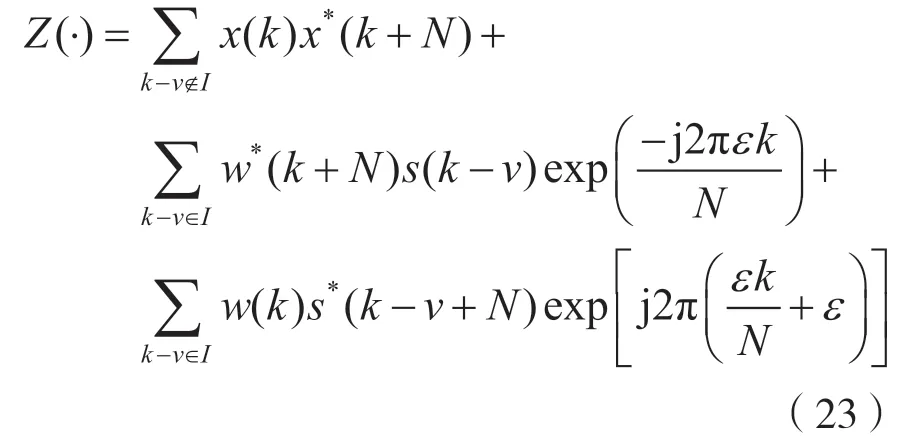
因為噪聲與OFDM 信號相互獨立，且CP 部分與除去CP 的OFDM 信號部分也相互獨立，所以根據中心極限定理，Z(·)可以近似為高斯分布的噪聲。當用于估計的OFDM 符號數目較大時，ε可表示為：

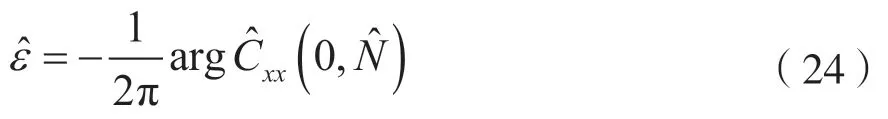
頻率偏移的估計為：

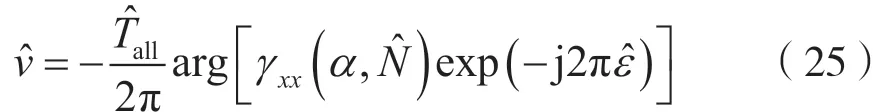
以N=64、G=16、FFT 長度為1 024 的OFDM信號為例，設該接收信號的有用符號共有100 個，OFDM 循環前綴CP 的最大長度為有用符號持續時間的1/4。圖1 表示在信噪比為5 dB 的情況下對OFDM 信號進行循環譜變換（τ=Ts），循環譜分析中FFT 點數取為4 096，其中橫軸表示循環頻率，縱軸表示循環相關函數值。

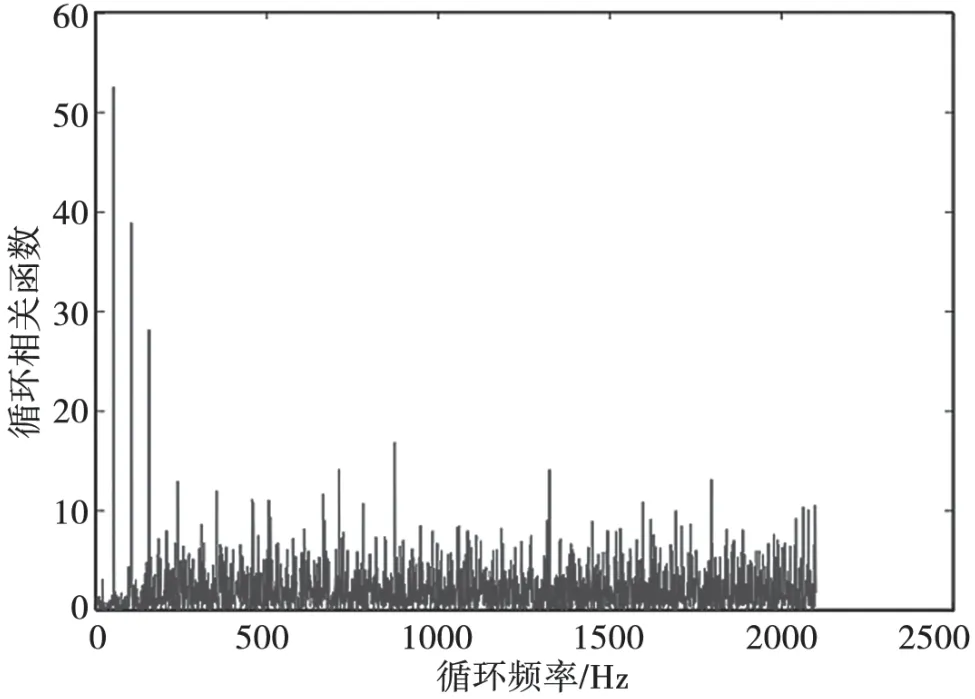
圖2 改進方法與傳統方法的性能比較

圖1 中可看出最左側位置有3 根較大值的譜線聚集在一起，對應于循環頻率及其倍數。在估計出CP 長度的參數信息后，還可進一步改善估計器的性能。根據前述的式（8）、式（20）、式（24）和式（25），可得=36。

3 仿真結果及性能分析

為了驗證本文識別方法的有效性，采用MATLAB 軟件進行仿真。仿真參數：OFDM 信號的采樣率設為100 MHz，接收信號共有50 個有用符號，子載波數目為N=64，循環前綴長度為G=16，過采樣因子為q=5/2，定時誤差為ε=0.3，頻率偏移為v=20Tb，Monte-Carlo 仿真次數為1 000 次，噪聲為加性高斯白噪聲。

3.1 仿真實驗1

采用基于循環譜分析的方法進行OFDM 信號參數估計識別，得出對過采樣因子、子載波數目、循環前綴長度和頻率偏移、定時誤差參數估計的歸一化最小均方誤差（Normalized Mean Square Error，NMSE）。仿真結果如圖3 所示，其中橫軸表示信噪比（單位dB），縱軸表示估計誤差。

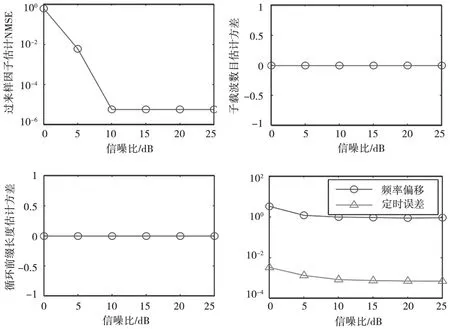
圖3 本文方法對OFDM 多參數的估計誤差曲線

從圖3 可以看出，本文的改進方法是一種有效的OFDM 參數估計識別方法。在信噪比大于5 dB 時，對OFDM 信號的過采樣因子、頻率偏移和定時誤差等參數估計的歸一化最小均方誤差都小于10-2。

3.2 仿真實驗2

分別對傳統基于最大似然判決的方法和本文改進方法進行估計識別性能的仿真對比分析，驗證對OFDM 信號多參數的平均識別正確概率結果。條件與前述的仿真實驗1 相同，仿真結果如圖4 所示，橫軸表示信噪比，縱軸表示不同估計識別方法的平均正確率。

由仿真結果可以得出，新方法比傳統的估計識別方法具有更好的性能，適用于認知無線電系統和其他非協作通信等應用對OFDM信號進行分析處理。

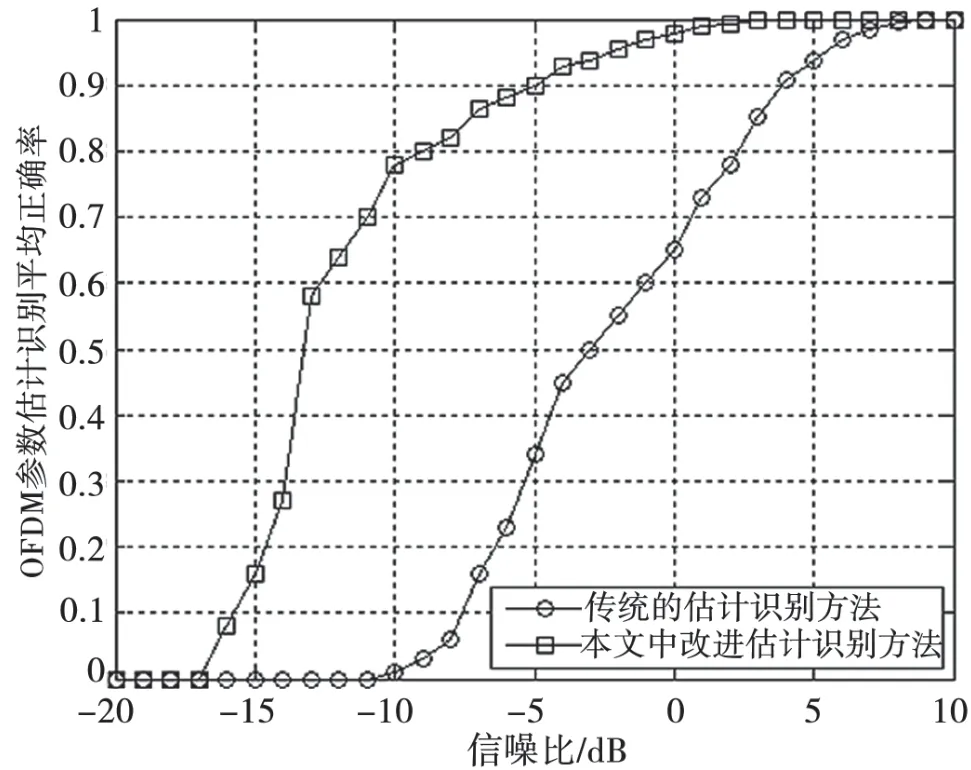
圖4 改進方法與傳統方法的性能比較

4 結語

隨著通信系統的不斷發展，OFDM 信號的應用越來越廣泛，作用越來越重要，使得所處的無線環境日益復雜，給OFDM 參數估計識別算法的研究提出了更高要求。本文提出了一種基于循環譜分析的OFDM 參數估計識別改進方法。仿真試驗表明，該方法比傳統識別算法性能更優，穩定性更好。今后將進一步拓展，為解決OFDM 信號參數估計識別問題提供更有效的手段，為無線電監測、智能化通信等領域的研究貢獻力量。