Glassy dynamics of model colloidal polymers:Effect of controlled chain stiffness?

Jian Li(李健), Bo-kai Zhang(張博凱), and Yu-Shan Li(李玉山),?

1Department of Physics and Electronic Engineering,Heze University,Heze 274015,China

2Department of Physics,Zhejiang Sci-Tech University,Hangzhou 310018,China

Keywords: glassy dynamics,colloidal polymers,molecular dynamics,mean square displacement

1. Introduction

Polymers are among the most studied materials for slow dynamics and glass transitions since they are difficult to crystallize due to their chain structure.[1-5]Lots of theoretical and numerical works have been devoted to fundamentally understanding their nonequilibrium slow dynamics and topological properties.[6-11]Chain structure and intramolecular barrier are two important polymer-specific features which cause the distinct dynamical behaviors of polymer melt from those of molecular liquids. For example, chain connectivity causes Rouse-like sub-diffusive motion of monomers at intermediate time.[7,12-14]Additionally,the intramolecular barrier plays an important role in glass transitions of polymers. Simulations and mode coupling theory(MCT)calculations on beadspring chains found that the increase of the intramolecular barrier strength increases the MCT exponent and MCT critical temperature.[15-20]

In recent years, attempts have been made to assemble“colloidal monomers,”e.g.,inorganic nanoparticles,into chain structures,termed“colloidal polymers”or“nanopolymers”or“nanochains.”[21]Colloidal polymers combine the features of both colloids (e.g., the large size of elements) and molecular polymers (e.g., the chain connectivity). Importantly, colloidal polymers provide a tool to observe glass transition in the real space with confocal microscope. In experiments,colloidal monomers form colloidal chains through attractive, directional, interparticle interactions, which are similar to covalent or supramolecular interactions in molecular chains.[21]In contrast to the high degree of structural control available in the synthesis of molecular polymers, methods to control fundamental structural features of colloidal polymers are still being developed.[22-26]However,colloidal polymers with tunable chain stiffness have been successfully assembled in experiments.[27-29]Similar to molecular polymers,chain stiffness can play an important role in glass transitions and slow dynamics of colloidal polymers. This stimulates us to study the effect of chain stiffness on glassy dynamics of colloidal polymers.

In our previous work,[30]we proposed a model to address the large monomer size of flexible colloidal polymers and study their glassy dynamics. We focused on the quantitative differences in the static structure and slow dynamics as the polymers vary from molecular chains to colloidal chains.Here, we build a model of colloidal polymer with controlled chain stiffness. By the new model, we employ molecular dynamic (MD) simulations to investigate the slow dynamics of the dense systems composed of colloidal polymers with controlled chain stiffness.The Newtonian dynamics is adopted instead of Brownian dynamics,because(1)the microscopic law of motion does not essentially influence the long-time glassy behavior;[31-34](2)we can thus use velocity-Verlet algorithm and large time step,i.e.,it is computationally more efficient.

The paper is organized as follows. We describe our colloidal polymer model with controlled chain stiffness and simulation method in Section 2. The results and discussion are given in Section 3. In Subsection 3.1, we report the results of static structure, including intrachain pair correlation and radial distribution function. The dynamic properties are reported in Subsections 3.2 and 3.3, such as the mean squared displacement,localization length,and Characteristic time. Finally, static and dynamic equivalences are discussed in Subsection 3.4. We summarize the paper in Section 4.

2. Model and simulation details

We use the purely repulsive Weeks-Chandler-Anderson potential, which is shifted to the surface (WCAS), to model the monomer-monomer excluded-volume interaction[35]

where r is the center-to-center distance between monomers,σ is the Lennard-Jones (LJ) diameter, and ε is the characteristic energy. The potential is cut off at rc=21/6σ. Δ is the diameter of the hard core of the colloidal monomers. Similar potential has already been used to study the self-assembling of polymer-tethered nanospheres and nanorods.[35]We change Δ to modify the monomer size.The potential reduces to the common WCA potential for molecular monomers when Δ =0.We define the nominal diameter of monomers as σp=Δ+rc,which is adjustable by the value of Δ. We adopt the LJ units,i.e., ε =1, σ =1, the Boltzmann’s constant kB=1, and the monomer mass m=1.

In addition to UWCAS,the bond connection between successive monomers along the chain is modeled by the finitely extensible nonlinear elastic springs (FENESs),[36]which is also shifted to the surface,

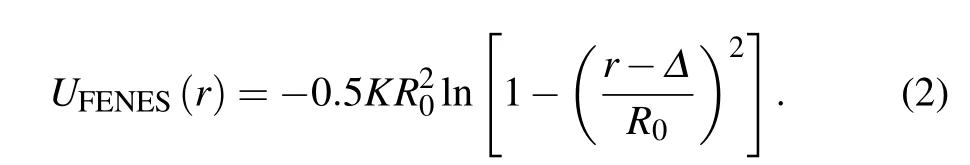
The parameters K =30 and R0=1.5. The composition of the WCAS potential and the FENES potential yields the effective bond potential with a sharp minimum at rb= Δ +0.9606. The bonded and non-bonded potentials prevent the chains from crossing. The incompatible length scales(σpand rb) and the flexibility of the chains make the system avoid crystallization.[6]Therefore, contrary to the colloidal system,polydispersity of monomer sizes is not required to generate the amorphous state at high volume fractions.

From the view of coarse-grained model,the major feature of colloidal polymers that is different from molecular polymers is the large monomer size (large repulsive core). In experiments, the colloidal polymers can be assembled through nanoparticles linked by coated polymer shell and the monomer size of the colloidal polymers typically varies from 5 nm to 60 nm.[21,23]Our model corresponds to this case of nanoparticles linked by coated polymer shell. Δ+rcis varied to represent the different sizes of the repulsive core.

The chain stiffness is controlled by a cosine harmonic bending potential,which acts on three consecutive monomers along the chain,

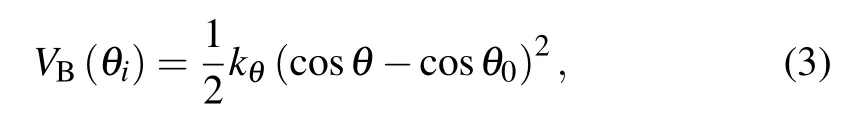
where θ is the bending angle between consecutive monomers i?1, i, and i+1 (2 ≤i ≤N ?1). The angle between adjacent pairs of bonds is maintained close to the equilibrium value θ0=180?,which can effectively represent the monomer directionality of the colloidal polymers. Additionally, the bending constant kθis varied to obtain different chain stiffnesses. The intuitive diagram of the chain of three monomers is shown in Fig.1,and the parameters σp,rb,and θ are marked.

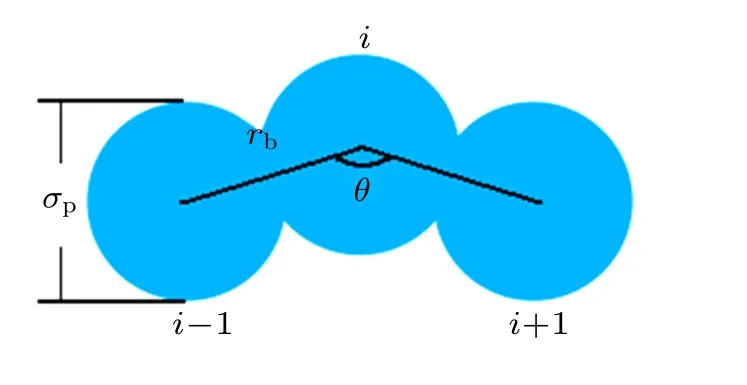
Fig.1. The intuitive diagram of the chain of three monomers.

3. Results and discussion

3.1. The static structural properties

The static structural properties of five chain stiffnesses for σp=4.0 and φ =0.575 are shown in Fig.2. The main peak of the radial distribution function (RDF) g(r) splits into two as a consequence of two incompatible local length scales, i.e., monomer size and bond length (Fig.2(a)). The strongest peak is located near rb/σp, contributed mostly by the jointed monomers, while the shoulder peak appears at r/σpcloser to 1, reflecting the characteristic distance of the excluded volume interaction between monomers. For stiff chains, i.e., kθ/= 0, a sharp maximum appears in the second peak of g(r). The reduced position and height of the sharp maximum shift differently to smaller and larger values for larger bending constant. The average intrachain pair correlation function ω(r) and histogram of bending angle n(θ) (inset) are shown in Fig.2(b). The position of the first peak of ω(r) corresponds to the distance between the jointed monomers too. ω(r)decays rapidly with r for flexible chains, reflecting that the intrachain correlation is very shortranged.However,ω(r)exhibits long-ranged periodic decayed peaks with r for stiff chains, and the position and height of the same-order peak shift to larger values for larger bending constant. The characteristic length between the (i ?1)th and (i+1)th monomers in a chain can be reflected by the peak’s position of the histogram of bending angle (Fig.2(b)inset). For flexible chains, i.e., kθ=0, two peaks emerge in the histograms of bending angles,which means there are two characteristic lengths. The positron of the first strong peak represents the characteristic length near σp, and the position of the second weak peak is close to that of the only peak of stiff chains. For stiff chains,the position of the only peak represents the characteristic length shifted to 2rb, and the position and height of the peak also shift to larger values for larger bending constant.

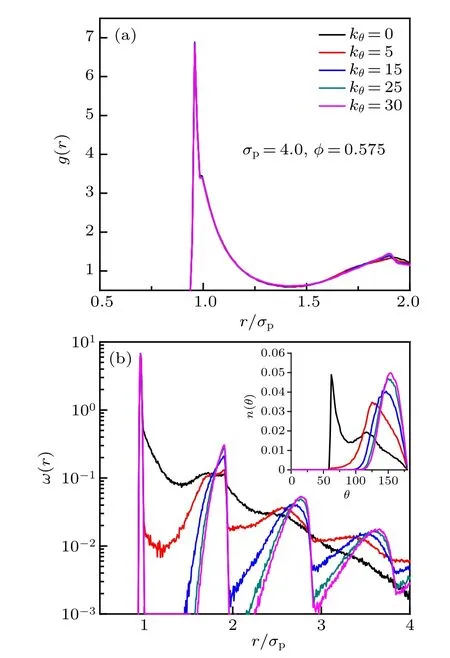
Fig.2. The static structural properties of five chain stiffnesses for monomersize and volume-fraction combination σp =4.0, φ =0.575. (a) The radial distribution function g(r). (b)The intrachain pair correlation function ω(r)and the inset shows the histogram of bending angle n(θ).

3.2. The mean square displacement

The mean square displacement (MSD) of monomers is defined as

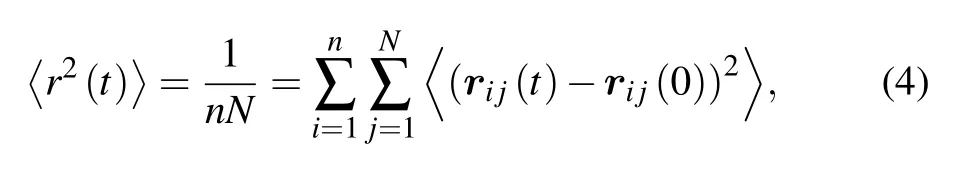
where rijis the position of the monomer j in the ith chain.The MSD of five chain stiffnesses for two monomer-size and volume-fraction combinations is shown in Fig.3. For flexible chains, three regimes are observed: ballistic regime, Rouselike subdiffusive regime,and normal diffusive regime.For stiff chains,a caging regime with significant smaller exponent or a horizontal plateau emerges after the ballistic motion, indicating the phenomenon of localization. At long time, MSD restores the sub-diffusive motion. The Rouse-like sub-diffusion of flexible chains happens in the displacement range between bond length rband end-to-end distance Re. These two lengths(squared) are marked out in Fig.3 as dashed lines. Revaries largely with chain stiffness, e.g., for combination σp=21/6,φ =0.78,Re=3.5 when kθ=0 and Re=6.7 when kθ=30;for combination σp=4.0,φ =0.575,Re=13.6 when kθ=0 and Re=26.2 when kθ=30. The sub-diffusion of monomers and diffusion of chains in polymer melts depend on many factors such as chain architecture, chain stiffness, chain length,and intrachain excluded volume interaction.[37-41]Different sub-diffusive regimes of monomers have been observed.[37-39]For our model of colloidal polymers, we find that the subdiffusive exponent α depends on the chain stiffness, which increases from 0.63 to 0.78 with the bending constant kθ(see Fig.3(c)).

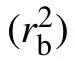
Fig.3. Mean square displacement〈r2(t)/σ2〉of monomers for fvie chain stiffnesses. (a) The monomer-size and volume-fraction combinations σp =21/6, φ =0.78. (b) σp =4.0, φ =0.575. The end points between ballistic and caging regimes are marked with open circles and those between caging and sub-diffusive regimes are marked with open squares. The square bond length and end-to-end distance of chains are marked out as dashed lines. (c)The sub-diffusive exponent α as a function of bending constant kθ for two monomer-size and volume-fraction combinations.

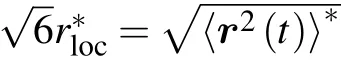
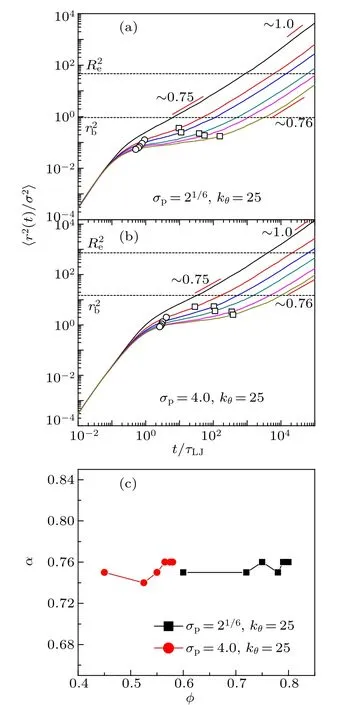
Fig.4. Mean square displacement〈r2(t)/σ2〉of monomers for stiff chains with bending constant kθ =25. (a)The monomer size σp=21/6 and the volume fractions are(from top to bottom)0.60,0.72,0.75,0.78,0.79,0.80. (b)The monomer size σp=4.0 and the volume fractions are(from top to bottom)0.45, 0.525, 0.55, 0.565, 0.575, 0.58. The end points between ballistic and caging regimes are marked with open circles and those between caging and sub-diffusive regimes are marked with open squares. The square bond length and end-to-end distance of chains are marked out as dashed lines.(c)The sub-diffusive exponent α as a function of volume fraction φ for two monomer-size and bending-constant combinations.

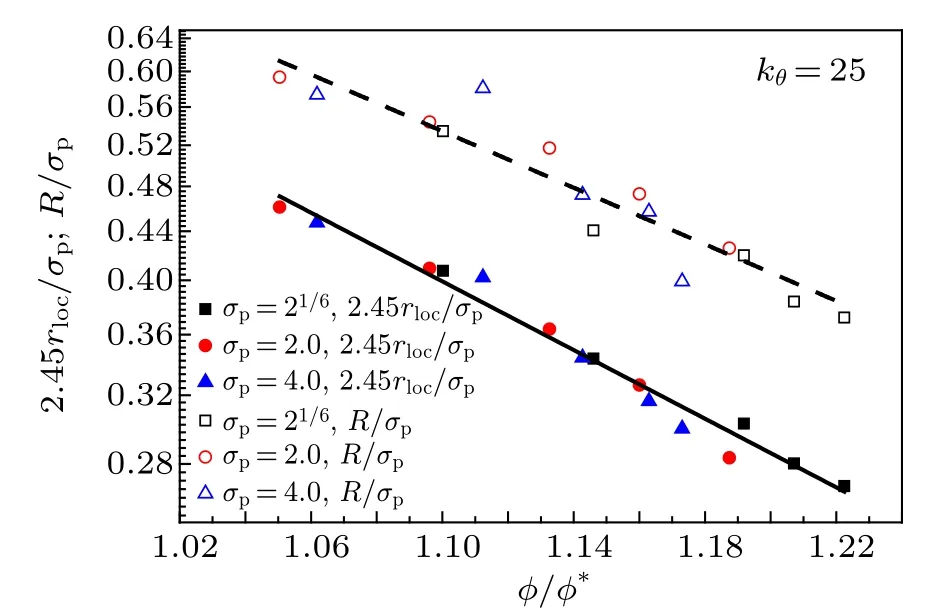
Fig.5. Log-linear plot of/σp (solid symbols) ?and R/σp (open symbols) as functions of scaled volume fraction φ/φfor stiff chains with bending constant kθ = 25. Two lines represent exponential relations rloc/σp ≈15.61exp(?3.33φ/φ?) (solid line) and R/σp ≈10.96exp(?2.75φ/φ?)(dashed line).

3.3. Characteristic time

Slow dynamics of glass forming liquids is often analyzed by the intermediate(self-)scattering function

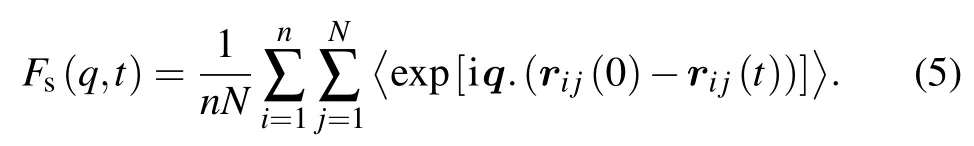
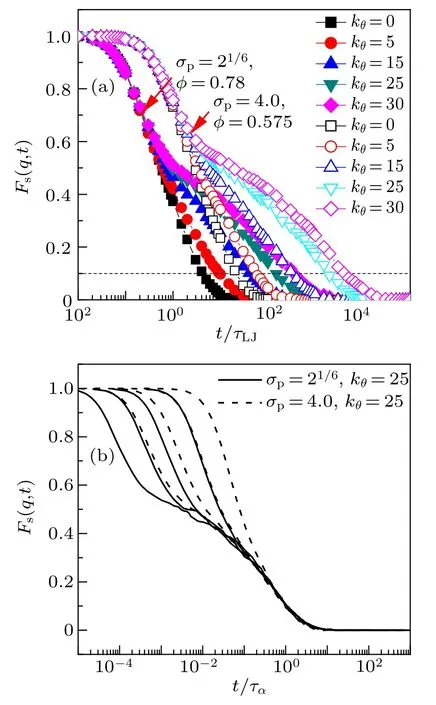
Fig.6.The incoherent intermediate scattering function Fs(q,t)for monomers.(a)The curves of σp=21/6,φ =0.78(solid symbols)and those of σp=4.0,φ = 0.575 (open symbols) for five chain stiffnesses. (b) The curves of σp = 21/6, kθ = 25 (solid line) for volume fractions (from left to right)φ =0.80, 0.79, 0.78, 0.75 and those of σp =4.0, kθ =25 (dashed line) for volume fractions(from left to right)φ=0.575,0.565,0.55,0.525.q is chosen to be the value corresponding the first peak of the static structure factor. The relaxation time τα is defined as Fs(q,t=tα)=0.1.

Such correlation function accounts for the loss in time of the memory of the initial structural configuration. Usually, the q is chosen to be the position of the first peak of the static structure factor. The Fs(q,t) for two monomer-size and volumefraction combinations at five bending constants is shown in Fig.6(a).For the two combinations,the Fs(q,t)decays slower as the increase of bending constants. We define the α relaxation time ταas when Fs(q,t=tα)=0.1. At long time,i.e., Fs(q,t)＜0.2, the decay of Fs(q,t) displays good time-(volume fraction) and time-(monomer size) superposition for stiff chains(see Fig.6(b)),which is in agreement with that of flexibale chains.[30]At short time, a two-step decay (caging)is observed.

Figure 7 shows the variation of τα/τLJas a function of bending constant kθfor three monomer-size and volumefraction combinations. τα/τLJexponentially increases with kθ,which can be well fitted by the formula

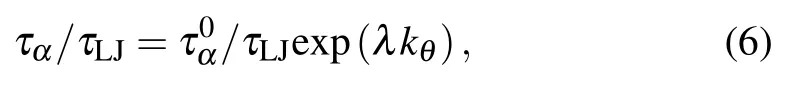
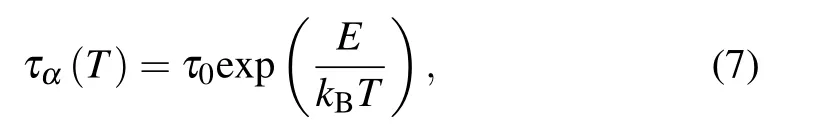
where E is the activation energy of the system. In our simulations,the reduced temperature is fixed at T?=1.0.Comparing the fitted formula and the Arrhenius behavior,we find that the increase of bending constant kθlinearly increases the activation energy E of the colloidal-polymer system.

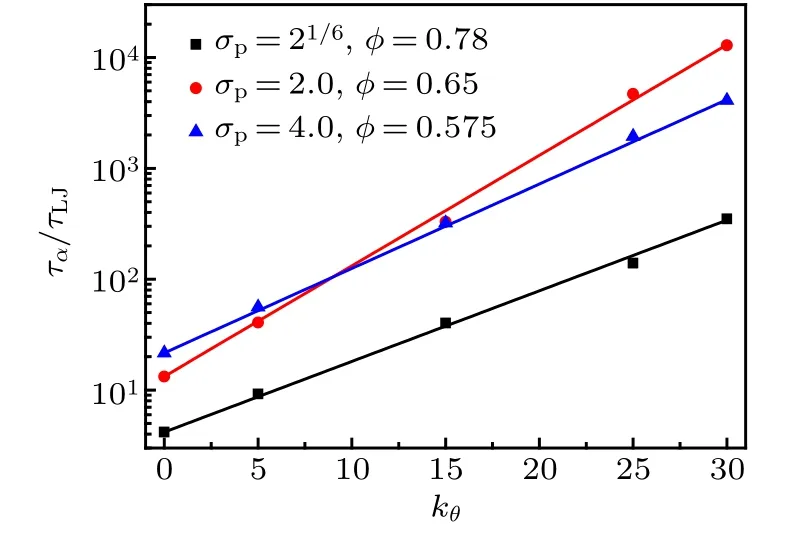
Fig.7. Log-linear plot of τα/τLJ as a function of bending constant kθ for three monomer-size and volume-fraction combinations,which is fitted by Eq.(6).

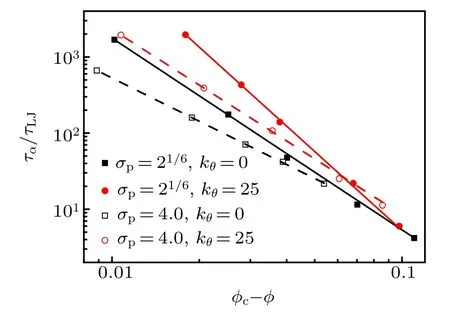
Fig.8. The relations between the α relaxation time and volume fraction for four monomer-size and bending-constant combinations are fitted by Eq.(8).

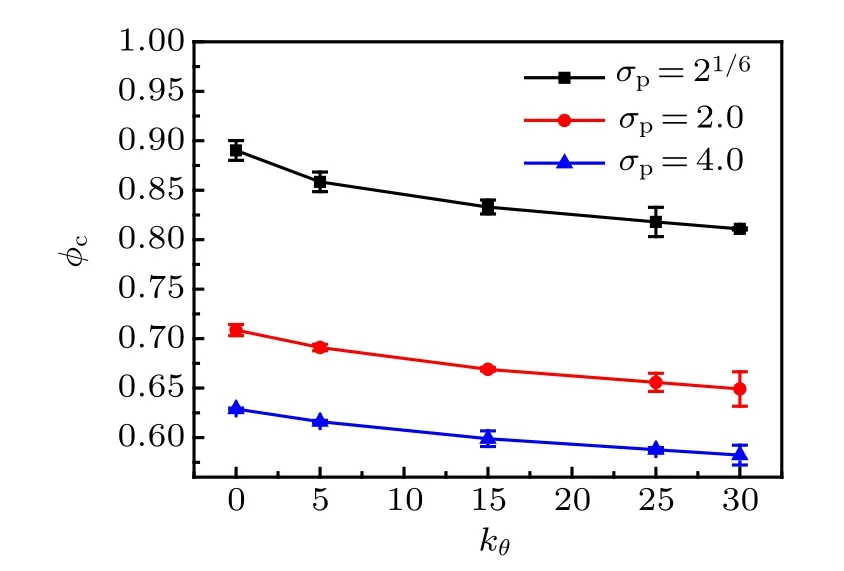
Fig.9. The MCT critical volume fraction φc as a function of bending constant kθ for three monomer sizes.

MCT theory predicts a power-law divergence of the α relaxation time as the MCT critical point is approached. For hard-sphere colloids, it is volume-fraction controlled and the power-law relation is written as

where γ ≈2.6 and φc≈0.52.[48]In Fig.8,we fit ταby Eq.(8)for four monomer-size and bending-constant combinations.We obtain φc= 0.89 and γ = 2.52 for σp= 21/6, kθ= 0;φc=0.82 and γ =3.44 for σp=21/6, kθ=25; φc=0.63 and γ =1.89 for σp=4.0, kθ=0; φc=0.59 and γ =2.44 for σp= 4.0, kθ= 25. We also fit ταby Eq. (8) for the other monomer-size and bending-constant combinations, and the critical volume fraction φcdecreases with bending constant kθfor three monomer sizes(see Fig.9).

3.4. Static and dynamic equivalences

In flexible colloidal-polymer systems, we find that the three colloidal-polymer systems(σp=21/6,φ =0.82),(σp=2,φ = 0.665), and (σp= 4,φ = 0.59) have the same hardshpere equivalent volume fraction φHS=0.503 and the hardshpere equivalent diameters are σHS=0.93, 1.766, and 3.72,respectively.[30]At this equivalent volume fraction (φHS=0.503), the RDFs (static quantities) coincide well at distance beyond the first peak, and the date of dynamic quantities(MSDs)collapse well onto the master curves.

In Fig.10,we check the static and dynamic equivalences of these three combinations in stiff-chain systems. For chains with bending constants kθ=5 and kθ=15, we find that the static RDFs do not coincide well because of the sharp maximums of the second peaks (see Figs. 10(a) and 10(b)), but the date of MSDs collapse well onto the master curves (see Figs.10(c)and 10(d)).

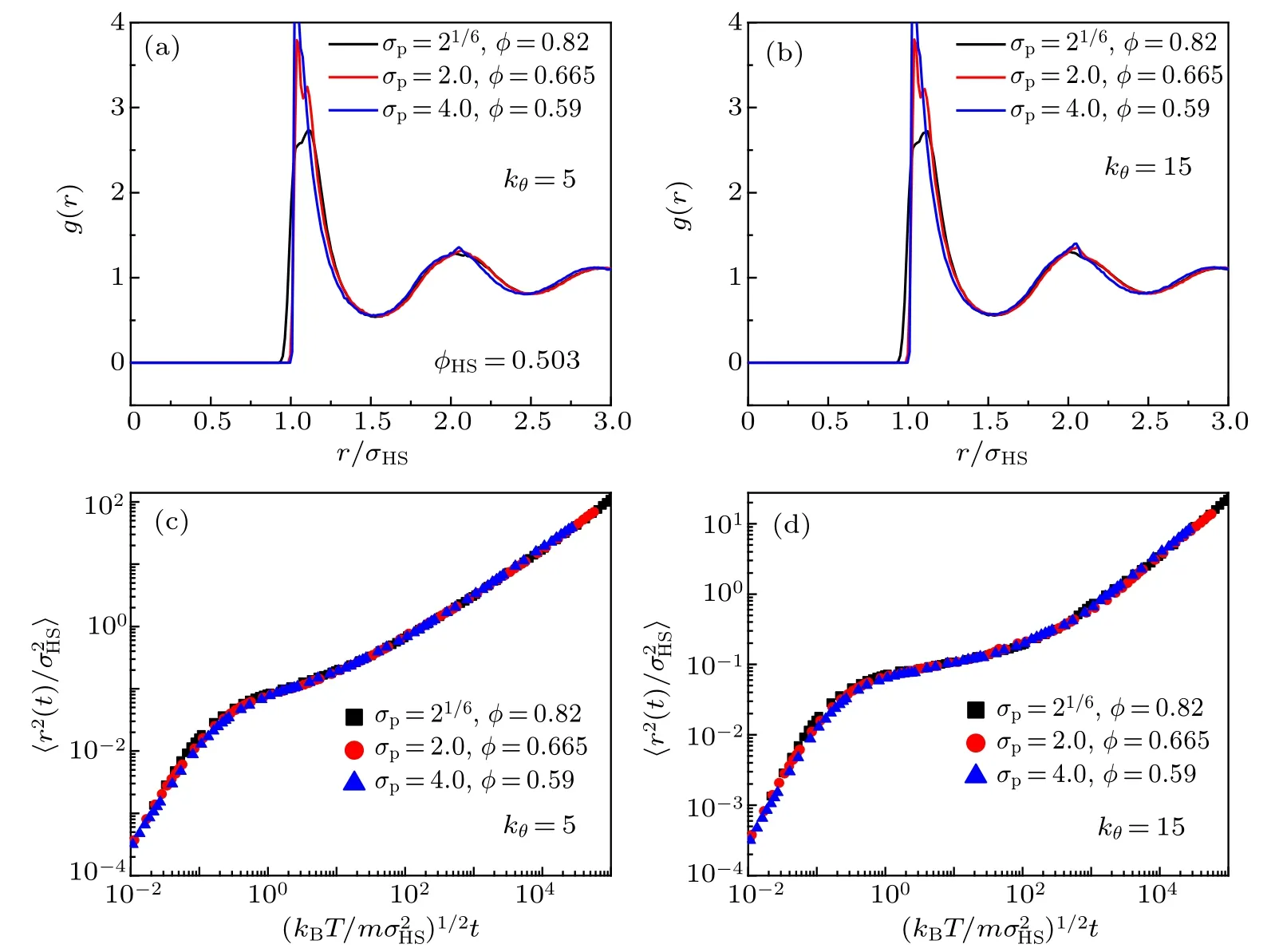
Fig.10. Static and dynamic equivalences for combinations (σp =21/6,φ =0.82), (σp =2, φ =0.665), and (σp =4, φ =0.59) in the stiffchain systems. (a)and(b)The radial distribution functions for chains with bending constants kθ =5 and kθ =15. (c)and(d)The mean square displacements for chains with bending constants kθ =5 and kθ =15.

4. Summary

In this paper,we model colloidal polymer with chain stiffness. We focus on the quantitative differences in the static structure and glassy dynamics of the colloidal polymers between flexible chains and stiff chains. The two incompatible local lengths, i.e., monomer size and bond length, are manifested in the split of the first peak of RDF. For stiff chains, a sharp maximum appears in the second peak of RDF. In contrast to the very short-ranged intrachain correlation of flexible chains,the average intrachain pair correlation function of stiff chains exhibits long-ranged periodic decayed peaks. The subdiffusive exponent of the MSD of monomers increases with chain stiffness.For stiff chains with bending constant kθ=25,when the volume fraction is above a threshold value φ?, a caging regime emerges in the MSD. As anticipated, φ?decreases with the increase of the monomer size: φ?≈0.65 for σp=21/6, φ?≈0.55 for σp=2, and φ?≈0.49 for σp=4.If φ?is used as the scaling unit for the volume fraction, the data of localization length versus volume fractions for different monomer sizes gather close to an exponential curve. The values of localization length of stiff chains are all larger and decay slower than those of flexible chains. Comparing the exponential fitted equation of the α relaxation time as a function of bending constant with the Arrhenius formula, it is found that the active energy of colloidal-polymer systems is linearly increased with the increase of chain stiffness.The α relaxation time of colloidal polymers can be well fit by the MCT powerlaw relation. The fitted values of φcare decreased with the increase of chain stiffness. Static and dynamic equivalences between stiff colloidal polymers of different monomer sizes have also been checked. We find that the curves of MSD can coincide well but the static RDF does not coincide well because of the sharp maximum of the second peaks. Finally, the model can be generalized to investigate more colloidal-polymer materials including the impacts of bond length, attractive force,and various topological structures.