基于線性回歸和MLP神經網絡的招標采購預測模型

龐鋮鋮，戎袁杰，劉昕，宋夢昕，王光旸

(國網物資有限公司，北京市 100120)

招標采購過程中，中標價格往往是招標人比較關注的結果，中標價格的高低對于招標人的預算管控、項目經營收益都存在著很大的影響。對于國家電網公司集中規模招標采購，采購頻次高，規律性較強，為了準確管控預算以及提升公司經營管理水平，利用集中規模招標歷史數據，提出兩種預測模型，即線性回歸模型和多層感知器[1](multi-layer perceptron，MLP)神經網絡模型，對招標采購項目的中標價格進行預測。

線性回歸的原理是通過含有自變量和因變量的線性等式來模擬兩個變量之間的關系，再將作為自變量和因變量的現有數據代入該線性等式，利用最小二乘法得到系數后，即可針對新的自變量預測因變量的變化趨勢。MLP神經網絡是典型的前饋神經網絡，該模型可以模擬人腦神經元存儲或學習大量輸入和輸出數據的行為，同時無需用變量描述映射關系，直接使用輸入和輸出數據構造模型，尤其對非線性關系具有較強的模擬能力。

本文以某種受原材料價格影響較大的變電設備為例，通過線性回歸和MLP神經網絡兩種方式，以實際數據為基礎對該變電設備報價進行預估，并對比不同方式預估價格的準確性。

1 線性回歸模型

簡單線性回歸分析是基于給定的單個解釋變量的回歸分析，用于研究單個因變量Y和單個自變量X之間的線性關系，線性回歸模型的一般形式為

Y=a+bX+ε

式中：a—常數項；

b—回歸系數；

ε—隨機誤差，即隨機因素對因變量所產生的影響。

采用最小二乘法得到模型參數估計值。

在得到線性等式后，還應采用統計檢驗來驗證該模型的正確性以及參數估計值的可信程度，通常使用的統計檢驗方法包括擬合優度檢驗、線性顯著性檢驗、變量顯著性檢驗，以及參數置信區間估計[2]。

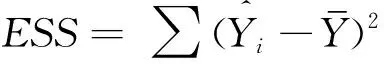
(2)方程總體線性的顯著性檢驗(F檢驗)，設定原假設H0∶R=0(線性不顯著)，其他假設Ha∶R≠0(線性顯著)，統計量F=[ESS/k]/[RSS/(n-k-1)]服從自由度為(k,n-k-1)的F分布。給定顯著性水平a(一般取0.05或0.1，即置信度為95%或90%)，查表得到臨界值Fa(k,n-k-1)，根據訓練樣本得出F的數值，通過F>Fa(k,n-k-1)來拒絕原假設H0(線性不顯著)，以判定原方程總體上的線性關系顯著成立。

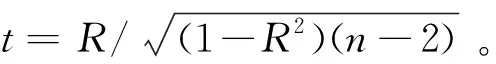
2 MLP神經網絡模型

神經網絡旨在模擬神經系統構造與功能進行數據處理，不斷調整模擬神經元之間的鏈條的權值，以使得整個網絡可以較好擬合訓練數據的關系。多層感知器是一種基于神經網絡的算法模型，其基本結構包括輸入層、隱含層以及輸出層，如圖1所示。每個輸入節點都通過一個加權的鏈連接到輸出節點，該加權的鏈用以模擬神經元之間的連接強度，訓練一個多層感知器就是不斷調整加權鏈的權值的過程，直至能較好地擬合訓練數據的輸入輸出關系為止[3]。

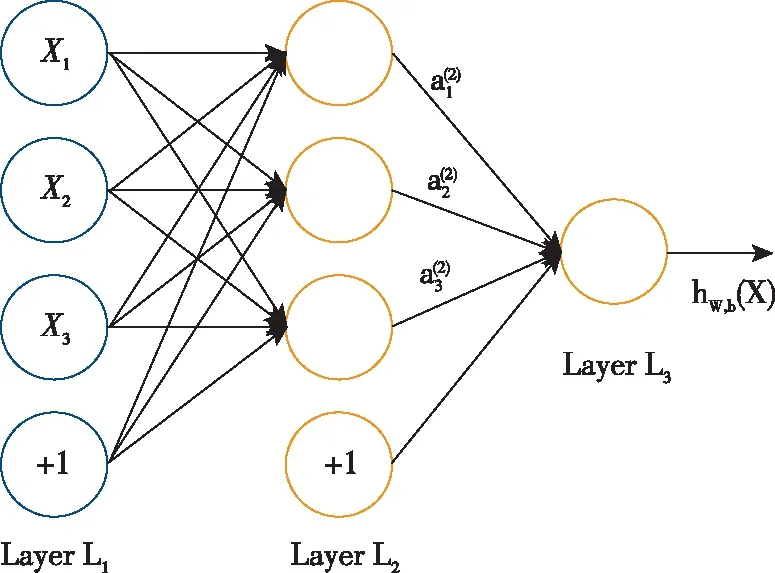
圖1 MLP神經網絡基本結構

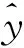
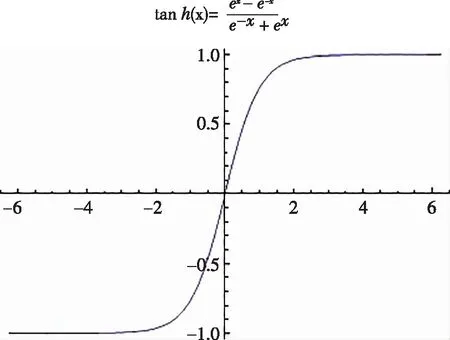
圖2 雙曲正切激活函數

多層感知器需通過不斷調整權值參數w來完成學習過程，直至輸出和訓練樣本的實際輸出一致，權值調整公式為

(1)

式中：wk—第k次循環后第i個輸入后鏈接的權值;

β—學習效率；

xij—訓練樣本xi的第j個屬性值。

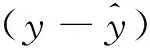
3 算例對比分析

以某變電設備產品為例，選取2010—2019年各采購批次原材料價格和變電設備中標價格作為訓練樣本，原材料價格作為自變量，變電設備價格作為因變量；同時選取兩種電壓等級產品作為研究對象，分別記為典型產品1和典型產品2，將同時利用線性回歸分析和MLP神經網絡模型對兩種典型產品進行預測。

3.1 簡單線性回歸模型

3.1.1 繪制散點圖

首先利用SPSS軟件將兩個變量的樣本數據作出散點圖，如圖3—圖4所示。從圖像層面上對兩個變量之間是否具有線性相關關系進行判斷，再進一步進行相關性分析。

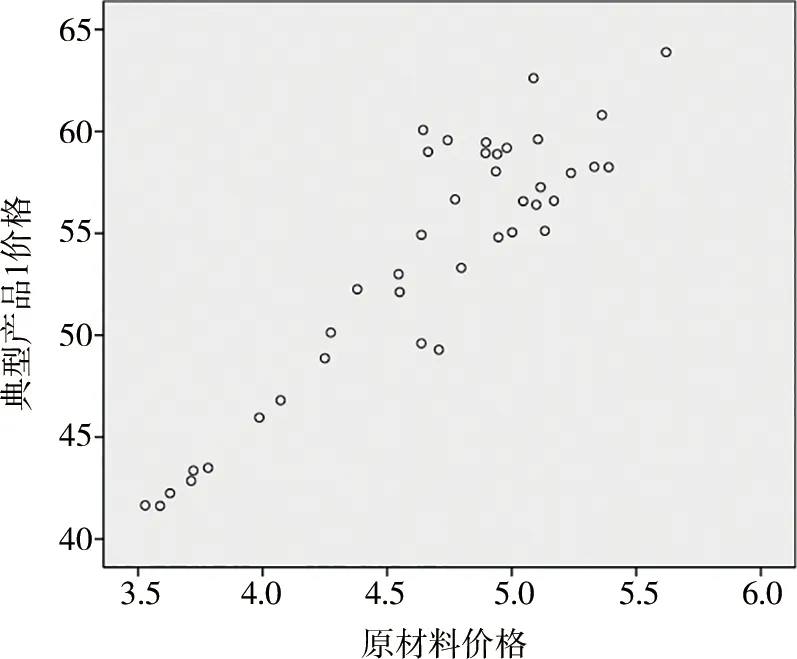
圖3 典型產品1價格與原材料價格關系散點

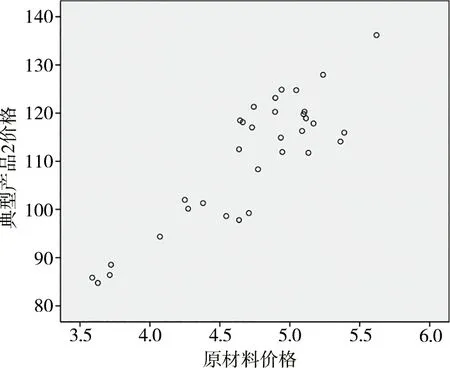
圖4 典型產品2價格與原材料價格關系散點

由圖3、圖4可以看出，兩個變量之間存在明顯的線性正相關關系，因變量隨自變量的增大而相應增大。相關系數是測定因變量和自變量之間相關關系程度及方向的指標[4]，計算公式為

(2)

相關系數越接近于1，相關性越強，反之則相關性越弱。計算典型產品價格和原材料價格的相關系數，得到結果如表1所示。對于兩種典型產品，其中標價格和原材料價格兩個變量之間的相關系數均超過0.8，呈高度正相關。

表1 變電設備價格和原材料價格的相關系數

3.1.2 建立回歸模型

利用SPSS軟件對訓練樣本數據進行回歸分析，采用最小二乘法建立模型參數的估計，根據輸出結果得到典型產品價格回歸模型。

典型產品1價格模型：

Y1=4.136 8X1+5.453 4

典型產品2價格模型：

Y2=8.933 6X2+5.356 5

3.1.3 模型檢驗

對上述線性回歸模型進行統計檢驗，選擇F檢驗與t檢驗。

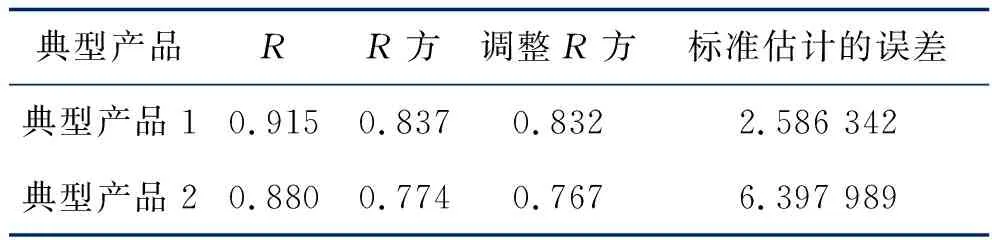
表2 模型匯總

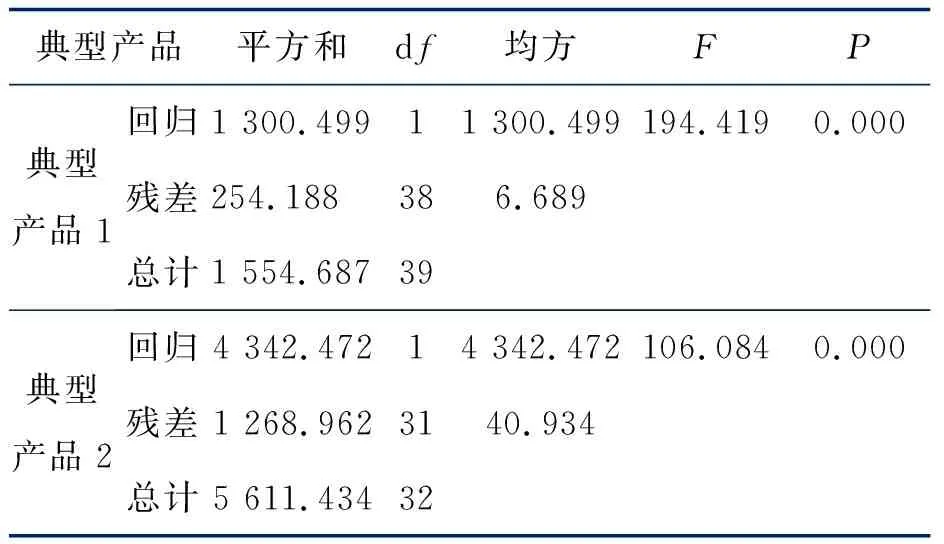
表3 Anovab

首先做擬合優度檢驗。表2數據顯示，從擬合優度來看，典型產品1價格模型：R=0.915，R2=0.837；典型產品2價格模型：R=0.880，R2=0.774。表明對于典型產品1，因變量總體變動量的83.7%可以被對應的線性方程解釋；對于典型產品2，因變量總體變動量的77.4%可以被對應的線性方程解釋。

接下來做方程總體線性的顯著性檢驗(F檢驗)。根據表3數據顯示，模型能夠較好地解釋總變動量。兩種研究對象的預測模型F檢驗量的P值趨近于0，小于0.01，故應拒絕線性不顯著的原假設，說明兩種變量之間存在顯著的線性關系。

最后做變量的顯著性檢驗(t檢驗)。通過t值計算式，可以得到兩種典型產品預測模型的t值分別為14.14和11.40。查詢t值表，發現t均落入拒絕域，故拒絕原假設H0，可得到R顯著的結論，說明自變量能夠顯著地解釋因變量。

3.2 MLP神經網絡模型

本文使用SPSS軟件對MLP神經網絡建模，分析過程主要分為分區數據集、訓練模型和預測結果三個步驟。

3.2.1 分區數據集

將活動數據集劃分為訓練集、測試集和驗證集三個集合，訓練集合中的數據用于訓練神經網絡，測試集合中的數據用來監視訓練過程中的錯誤以防過度訓練，而驗證集合中的數據則用于評估訓練所得到的神經網絡的準確性。該案例中，訓練、測試和驗證樣本指定7、3、0，即按70%、30%和0%的比例來劃分樣本，再將樣本數據隨機分配到三種樣本集合中。

3.2.2 訓練模型

在滿足精度要求的前提下，為了提高數據訓練效率，在該神經網絡的體系結構中構建一個使用雙曲正切激活函數的隱藏層，并選擇批處理的訓練方式，即運用訓練數據集中的所有記錄信息，以使得總誤差最小化。由于該方法在滿足任何結束訓練的條件前都需要不斷調整權重，所以存在將數據傳遞數次的可能性。優化算法在調整后選擇了相應的共軛梯度，模型參數如圖5—圖6所示。兩種典型產品的平方和誤差為2.607%和2.952%，相對誤差分別為0.168%和0.236%。

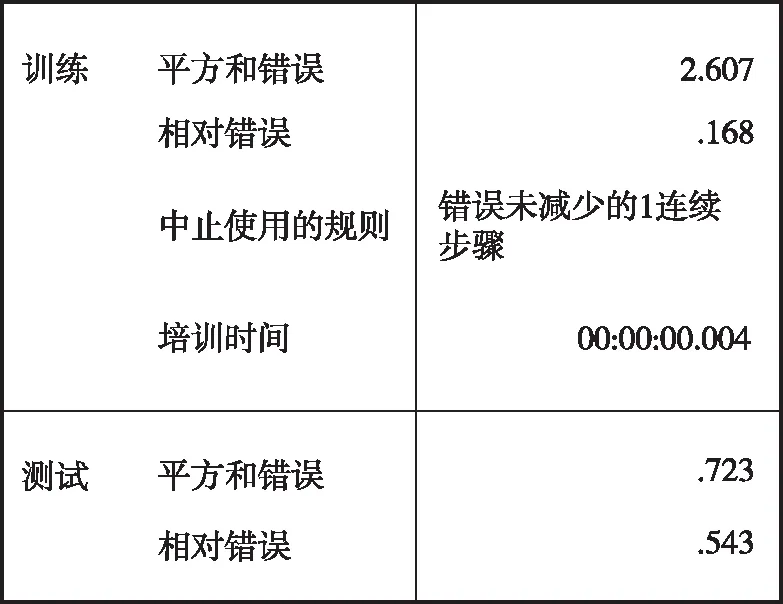
圖5 典型產品1預測模型匯總

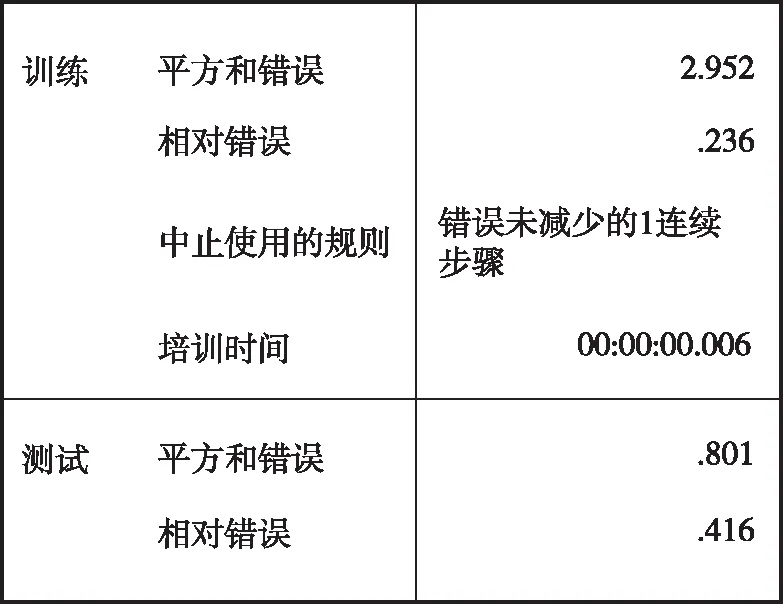
圖6 典型產品2預測模型匯總

3.2.3 預測結果

通過訓練樣本得到滿足要求的神經網絡模型，預測如圖7—圖8所示，殘差分析如圖9—圖10所示。

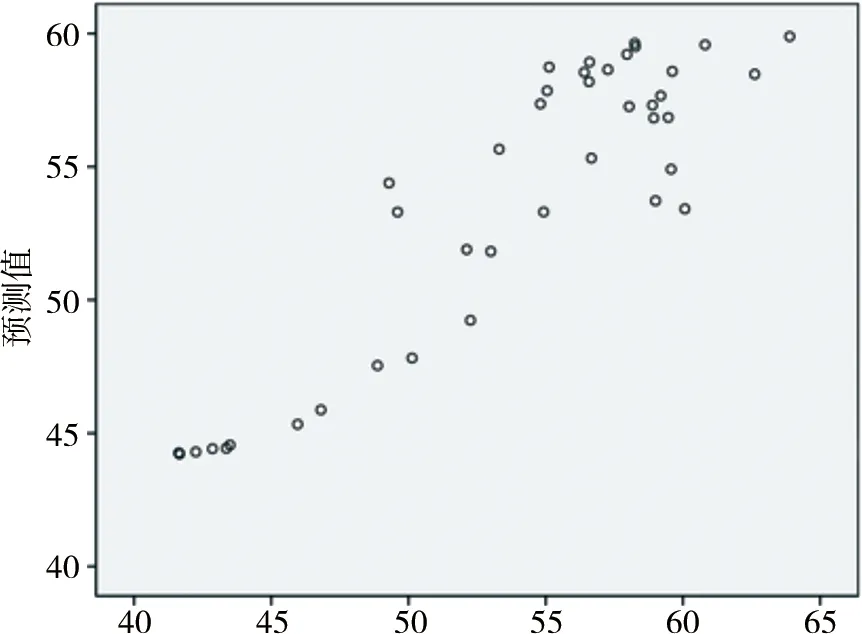
圖7 典型產品1模型預測

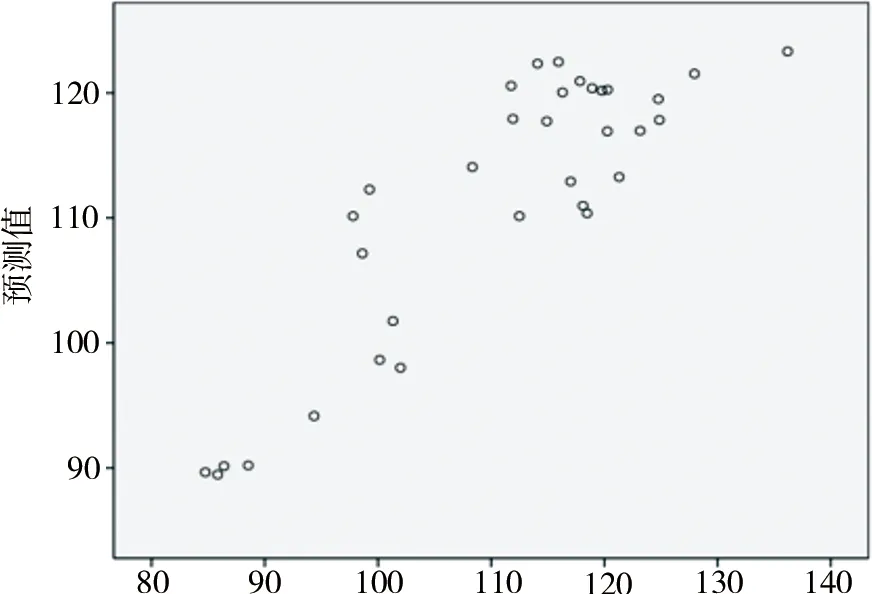
圖8 典型產品2模型預測

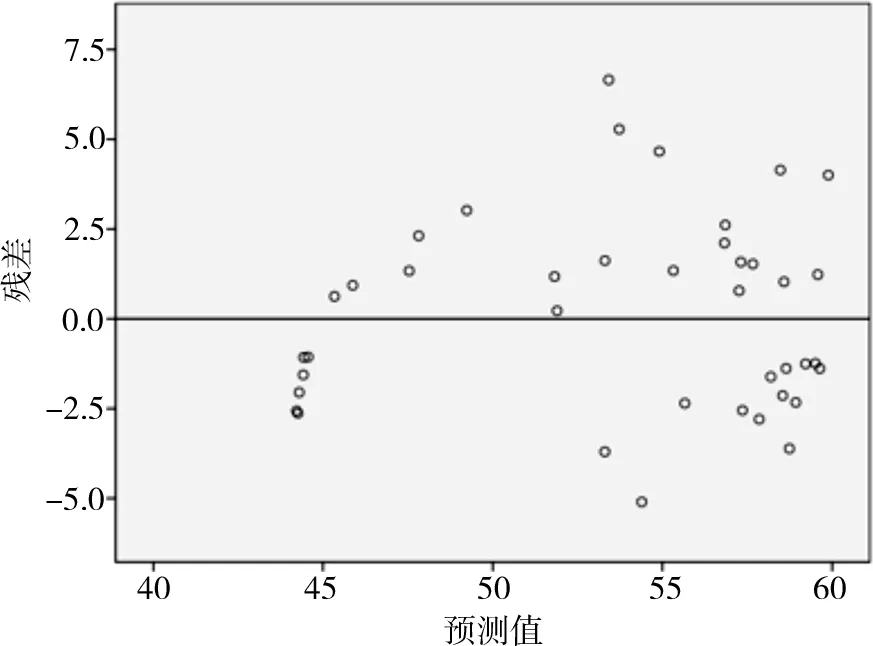
圖9 典型產品1殘差分析

由圖9和圖10可以看出，典型產品1殘差在±5以內，典型產品2殘差在±15以內，均在可接受范圍內。

4 模型預測效果

本文采用平均相對誤差(ARE)和標準誤差(SE)兩個指標[5]來評價上述兩種模型的預測準確性。標準誤差(SE)也是描述預測值與實際值之差的一種度量，其值越小，預測精度越高。平均相對誤差和標準誤差公式分別為式(3)、式(4)：

(3)

(4)

式中：yi—實際值；

n—預測樣本數。

通過計算得出具體數值，見表4。

表4 預測誤差估計結果

由表4可知，兩種預測結果的平均相對誤差和標準誤差數值均較小，平均相對誤差都在5%以內，標準誤差在5%左右。此外，由于本文所研究的變電設備，其價格與原材料價格線性關系較為凸顯，所以，無論是將平均相對誤差還是標準誤差作為判斷指標，對于兩種典型產品，線性回歸模型預測精度略優于MLP神經網絡，但兩模型預測精度差異并不是十分顯著。兩種方法在進行變電設備價格預測時均有一定的參考價值。

5 結 論

通過SPSS軟件，建立線性回歸和MLP神經網絡兩種模型，對某種變電設備招標采購中標價格進行預測。預測結果說明：

(1)兩種模型的預估值與真實值的平均相對誤差和標準誤差都較小，對于投標價格受原材料價格影響較大的變電設備，兩種模型都可以對招標采購價格做出較為精準的預測，均具有一定的參考價值。

(2)對于與原材料價格線性關系較為凸顯的產品，兩種模型的預測能力不相上下，線性回歸模型預測精度略優于MLP神經網絡模型，但隨著訓練樣本集的增大，MLP神經網絡模型的預測能力可能更強。

綜上，兩種模型在招標采購中變電設備價格預測上并不存在絕對的優劣，模型的預測精度與變電設備的類別有一定相關性。在實際應用中，可以結合線性回歸模型和MLP神經網絡模型對變電設備價格進行綜合判斷。