例談初中數學數形結合思想的有效運用

白東曉

初中數學研究的對象主要分為數和形兩大部分，即為代數與幾何，數與形之間存在著緊密聯系，該聯系稱之為數形結合。教師在平常教學中需有效應用數形結合思想，把數與形有機整合起來，為學生提供新穎的學習思路，幫助學生鞏固數學基礎，提高解題能力。

一、運用數形結合思想，輔助學生理解概念

概念屬于數學知識體系中的基礎，不僅是學生學習其他知識的鋪墊，還是進行解題的重要支持與關鍵所在。在初中數學課程教學中，教師要高度重視概念教學，概念以文字性描述為主，如果僅僅依靠語言描述顯得過于抽象，學生很難真正理解，在解題環節無法做到靈活自如運用。這時可運用數形結合思想，把描述概念的文字以圖形形式來呈現，更為直觀與具體，輔助學生更好地理解概念，為后續學習做鋪墊。

例如在進行“相反數”教學時，教師先要求學生畫出一個數軸，注意原點、正方向和單位長度，在數軸上找出表示3和-3、-5與5、2.5和-2.5各組數的點。

思考：表示每對數的點有什么相同和不同之處？鼓勵學生結合數軸的相關知識自由回答，使其獲得感性認知。

教師指導學生認真觀察、討論和研究各對數的特點，分析每組數所對應兩個點的位置關系有什么規律？使其初步發現每對點位于原點左、右兩邊，且距離原點等距。提出問題：數軸上與原點的距離是1的點有幾個？6呢？這些點表示的數分別是什么？觀察后學生知道都有兩個，分別是1與-1，6和-6。

師生一起歸納：每組中的兩個數只有符號不同，它們所對應的兩點分別在原點的兩側，到原點的距離相等。引導學生總結相反數的概念：像3和-3、-5和5、2.5和-2.5這樣只有符號不同的兩個數稱互為相反數，讓學生理解代數概念與幾何意義。

教師運用學生熟悉的數軸講述和解析相反數的概念，讓學生體會數形結合思想。

二、應用數形結合思想，講授數學公式定理

在初中數學教學過程中，公式與定理占據著非常重要的地位，是理論知識的高度濃縮與精華，學生在解題時離不開公式和定理的輔助。當講授到公式與定理時，同樣可以應用數形結合思想，以幾何圖形的形式把數學公式與定理展示出來，喚起學生的感性思維，降低學習和理解難度。

例如在開展“平行線的判定”教學時，學習平行線的判定公理，教師先帶領學生回顧平行線、平行公理及其推論等知識。

問：如何用平行線的定義及平行公理來說明兩條直線平行？

根據學生的回答加以總結：如果用平行線定義難以說明兩條直線沒有交點，平行公理的推論對條件要求較多，要有三條平行線，且其中的兩條分別與第三條平行，能否用這兩種方法來說明木工師傅用拐尺畫平行線的原理？使其嘗試說明，聯想到有其他途徑判定兩條直線是否平行。

回憶、敘述用三角板和直尺過一點P畫已知直線AB的平行線的過程，設疑：這種畫法實際上是畫一對什么角相等？使其觀察圖形后發現這兩個角是直線AB、CD被EF截得的同位角，引領學生總結出平行線的判定方法1，簡單記為“同位角相等，兩直線平行”。隨后教師繼續應用數形結合思想，指導學生借助“三線八角”圖探索平行線的判定方法2與3。教師引導學生動手畫圖，應用數形結合思想講授新知識，使其在探索圖形的過程中，學會思考和探索。

三、發揮信息技術優勢，體現數形結合思想

數形結合思想的兩個部分是“數”與“形”，其中“形”具有直觀性，能夠具體、形象地把數學理論知識呈現出來。在新課改背景下，信息技術已經廣泛運用至各行各業，自然也包括教育領域。教師在日常教學中，應該充分發揮信息技術的優勢，運用現代教育手段拆分與組合圖形，更為生動地體現出數形結合思想，把圖形的轉化變得更加科學與合理，帶給學生強烈的視覺沖擊，以便輕松理解與掌握新知識。

在實施“菱形”教學時，教師可以提前通過網絡平臺搜集一組生活中的菱形實物圖片，如：鐵絲網、室內掛衣架、春聯中的“福”字、瓷片和三菱車標等，讓學生認真觀察，從中找出菱形，引出課題，使其類比矩形的定義，結合信息技術手段，動態展示將平行四邊形較短一邊進行平移的過程，讓學生通過觀察、分析與討論，順利抽象出菱形的定義。

提問：菱形具有哪些性質？組織學生結合圖片分組討論后全班交流，一起歸納：菱形的四條線都相等;兩條對角線相互垂直，且每一條對角線平分一組對角;面積等于對角線乘積的一半。設疑：假如一個四邊形是一個平行四邊形，只要再添加什么條件才能判定它是一個菱形？有什么根據？

學生先畫圖，再討論，根據菱形的定義得知：只要再添加一組鄰邊相等的條件就能判定該平行四邊形是一個菱形。隨后教師繼續借助信息技術手段，指導學生在觀察與實踐中探究菱形的其他判定方法。

通過信息技術和動手操作，引領學生親身經歷探究菱形定義、性質和判定方法過程，體現數形結合思想，使其充分享受到視覺盛宴，培養學生觀察、猜想及合情推理能力。

四、合理使用以形助數，鍛煉學生解題技巧

想更好地運用數形結合思想，不能僅僅停留在理論知識的講授方面，還要擴展至解題環節，為學生提供親自運用數形結合思想的機會，使其深刻體會到數學思想方法的妙用，幫助學生找到便捷的解題方法。具體來說，數形結合思想分為以形助數、以數解形兩種情形，教師可以指引學生合理使用以形助數的方法處理題目，借助形的幾何直觀性來闡明數之間的關系，將復雜問題變得簡單化，鍛煉學生的解題技巧。

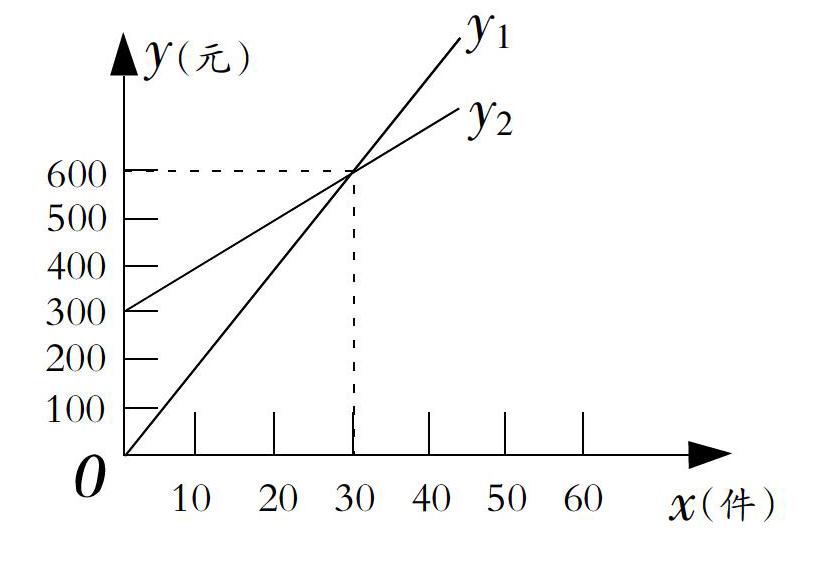
以“一次函數”教學為例，設置題目：某公司推銷一種產品，設x（件）是推銷產品的數量，y（元）是推銷費，如下圖所示，表示公司每月付給推銷員推銷費的兩種方案，看圖解答下列問題：

（1）求y1和y2的函數解析式;

（2）解釋圖中表示的兩種方案是怎么付推銷費的？

（3）假如你是一名該公司的推銷員，應該如何選擇付費方案？

解析：（1）教師指引學生自學觀察圖形，根據兩個一次函數圖像及坐標軸上的點展開分析，得出兩個解析式分別為y1=20x，y2=10x+300;

（2）依據一次函數相關知識自主組織語言，指導學生運用數學術語來描述這兩種付推銷費的方案，y1是不推銷產品沒有推銷費，每推銷10件產品將會得推銷費200元，y2則是保底工資300元，每推銷10件產品能夠得到提成100元;

（3）根據業務能力高低來選擇付費方案，如果業務能力強，平均每月保證推銷不少于30件時，就選擇y1的付費方案;否則選擇y2的付費方案。

在上述案例中，學生解題的關鍵在于以形助數，知道圖像在上方的說明它的函數值較大，反之較小，兩圖像相交時，說明在交點處的函數值相等，改善其解題能力。

數形結合就是把抽象的數學語言、數量關系與直觀的幾何圖形、位置關系結合起來，以數解形則是部分圖形太過于簡單，直接觀察卻看不出什么規律，需要給圖形賦予一定的值，如邊長和角度等，把抽象問題變得具體化，優化學生的解題思路，順利解題。教師在解題教學環節，指導學生巧妙采用以數解形的方法分析與處理題目，將數學問題變得更加充實與豐滿，使其找到清晰的解題思路，最終得出準確的答案。

教師要充分認識到數形結合思想的教育價值與積極意義，把握好概念、公式、定理、公理等講授同解題實踐之間的關系，從多個方面滲透數形結合思想，幫助學生深刻理解與牢固掌握理論知識，提升解題水平。

■ 編輯/王? ? 波