雙饋風力發電場無功支撐范圍的魯棒估計

周 瑜，李正爍

（1.山東大學電氣工程學院,山東省濟南市250061；2.電網智能化調度與控制教育部重點實驗室（山東大學）,山東省濟南市250061）

0 引言

風電等新能源具有較強的隨機性和間歇性,大規模并網給電網無功平衡帶來了新挑戰［1］。為保證電壓水平,電網亟需無功源。但是,新能源并網可能減少傳統無功源。例如在德國,新能源增加使得一部分可為電網提供無功的傳統火力發電廠關閉［2］。因此,電網亟需尋找新型無功源。

近年來,雙饋風力發電場并網數量不斷增加,可作為新型無功源參與電網優化。其原因為［3-5］:①雙饋異步發電機（doubly-fed induction generator,DFIG）可輸出連續可調的無功功率,通過有功和無功解耦控制,無功調節不會影響有功功率［6］；②風電場內的并聯電容器組及靜止無功補償裝置/靜止無功 發 生 器（static var compensator/static var generator,SVC/SVG）可以輸出無功功率［7］；③有載調壓變壓器（on-load tap changer,OLTC）分接頭擋位可調節風電場輸出的無功功率。

無功調節范圍必須是確定的,否則調度中心無法對其制定合適的調度指令。但風電場無功支撐范圍受多種因素影響,難以準確估計。影響因素包括:①風電場和電網的公共接入點（point of common coupling,PCC）的電壓設定值和DFIG有功功率具有不確定性（此處電壓設定值指的是當風電場按照電網指令提供無功功率時PCC的電壓設定值,該值通常由電網指定,而在估計風電場無功支撐范圍時尚未確定,因而是不確定量）；②OLTC分接頭擋位和并聯電容器組投切狀態等變量的離散性；③風電場內部潮流方程具有非線性。這些都對估計無功支撐范圍帶來了挑戰。

目前,對雙饋風力發電場無功功率的研究主要集中在風電場內部的無功電壓控制［8-11］,亦有部分文獻提出將風電場作為無功源參與電網無功優化［3-5］。文獻［3］提出利用雙饋風力發電場對本地用戶進行就近無功補償。文獻［4］提出將雙饋風力發電場作為連續可調無功源參與配電網的無功優化。在此基礎上,文獻［5］分析了同步發電機和雙饋風力發電場的“無功計價模型”,建立了有功網損和無功購買費用最小的目標函數。上述研究證明了將雙饋風力發電場作為新型無功源參與電網無功優化的可行性和優勢。但是,它們將風力機單體無功容量上下限進行線性疊加來近似計算風電場整體的無功支撐范圍,忽略了不確定性、非線性和離散性等因素對于風電場無功支撐范圍的影響。

受文獻［12］啟發,本文考慮不確定性、非線性和離散變量等因素,提出面向雙饋風力發電場無功支撐范圍的魯棒估計方法。

1）建立契合于風電場無功支撐范圍估計的兩階段魯棒優化模型:第1階段給出候選的最大無功支撐范圍；第2階段檢查在不確定性場景下,該無功支撐范圍是否可行。

2）優化模型考慮了DFIG有功功率和PCC電壓幅值的不確定性,并聯電容器組和SVC/SVG的無功輸出能力,以及OLTC分接頭擋位調節等因素對風電場無功支撐范圍的影響。

3）采用對偶轉化和錐松弛等方法對兩階段魯棒優化模型進行可解性處理,基于列約束生成（column-and-constraint generation,C&CG）算 法 對兩階段優化模型進行求解。

4）給出風電場作為無功源參與電網無功優化的策略。它由無功支撐范圍計算、電網無功優化和風電場內無功動態追蹤3個步驟組成。

1 雙饋風力發電場運行模型

1.1 內部網絡約束

風電場內部網絡一般為輻射狀結構［13］,功率方程可采用DistFlow模型［14］。該模型便于進行錐松弛,可簡化兩階段魯棒優化模型的求解［15-16］。采用DistFlow模型的風電場網絡約束方程為:

式中:B為風電場內所有節點集合；T(j)為以節點j為首端節點的支路末端節點集合；Z(j)為以節點j為末端節點的支路首端節點集合；pG,j和qG,j分別為節點j的DFIG有功輸出和無功輸出；qS,j為節點j的SVC/SVG無功注入；qC,j為節點j并聯電容器組的無功注入；pD,j和qD,j分別為節點j的有功負載和無功負載,取值通常為0；pij和qij分別為線路(i,j)的有功潮流和無功潮流；rij和xij分別為線路(i,j)的電阻和電抗；lij為線路(i,j)的電流幅值平方；vj為節點j的電壓幅值平方；tij為線路(i,j)的OLTC變比,若線路(i,j)沒有調節變壓器,則tij=1。式（1）和式（2）分別表示任一節點的有功和無功功率平衡；式（3）表示任一線路兩端電壓降與線路電流和流經功率的關系；式（4）或式（5）為用于表示支路首節點有功功率和無功功率與該節點電壓和流出電流關系的2種等價數學形式。

方便起見,設節點1為PCC。為求解風電場無功支撐范圍,添加如下約束:

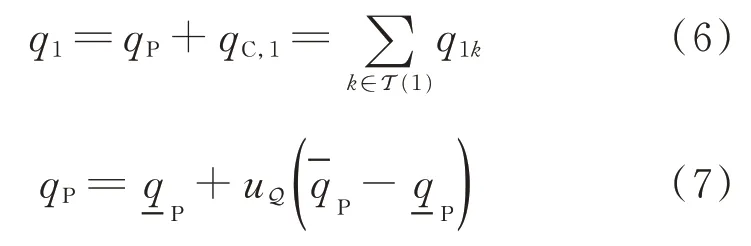
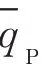
式（6）為式（2）中j=1時的特例,PCC相連支路損耗考慮在其下游節點的式（1）和式（2）中；式（7）對qP做了等價轉換,以便于后續求解。

1.2 DFIG有功功率約束

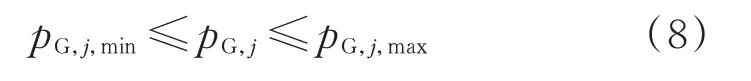
式中:pG,j,max和pG,j,min分別為節點j的DFIG有功功率pG,j的上、下限。

1.3 DFIG無功功率約束

DFIG無功功率可調范圍通常受有功功率波動影響。本文參考文獻［4］,將DFIG有功功率預測范圍上界對應的無功功率可調范圍作為DFIG無功功率約束。這其實是對DFIG實際無功可調范圍的保守估計,但可簡化后續計算。相關說明參見附錄A。該約束形式如下:

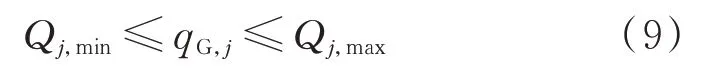
式中:Qj,max和Qj,min分別為節點j的DFIG輸出無功功率qG,j的上、下限,在后續優化中為常數,數值可由附錄A中方法確定。

1.4 SVC/SVG無功功率約束

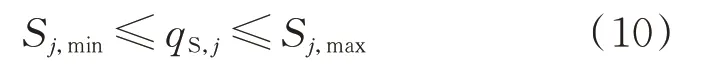
式中:Sj,max和Sj,min分別為節點j的SVC/SVG無功功率qS,j的上、下限。

1.5 電壓幅值平方約束

PCC電壓幅值v1約束如下:

式中:vset為PCC電壓幅值設定值的平方,為不確定量。

其他節點電壓幅值平方vj約束如下:

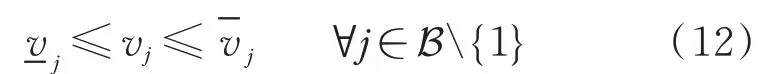
1.6 電流約束

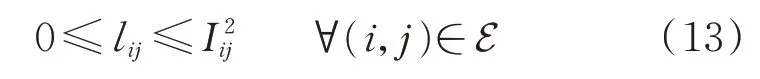
式中:Iij為線路(i,j)上電流幅值的上限；集合E為風電場內所有支路集合。

1.7 并聯電容器組約束

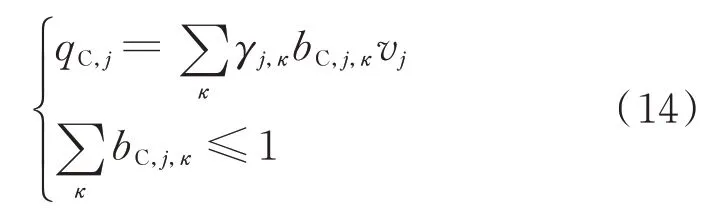
式中:bC,j,κ為0-1變量,且bC,j,κ∈{0,1}。

其 中,式（14）中 的bC,j,κvj為 雙 線 性 項,利 用McCormick方法對其進行線性化處理［17］:

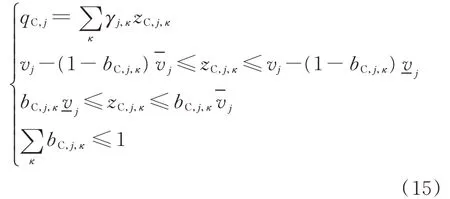
式中:zC,j,κ為輔助變量。

1.8 OLTC的約束

設支路(i,j)的OLTC分接頭有kT擋,分別為Tij,1,Tij,2,…,Tij,kT,需滿足以下約束:

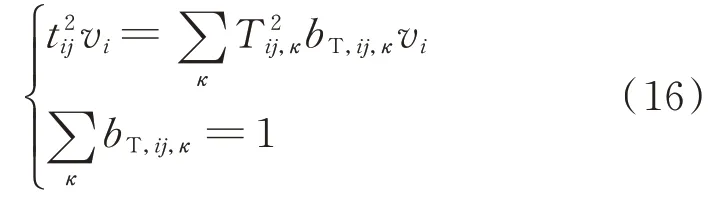
式中:bT,ij,κ為0-1變量,且bT,ij,κ∈{0,1}。

對 式（16）中 的 雙 線 性 項bT,ij,κvi,同 樣 采 用McCormick方法處理,轉換后的形式如下:

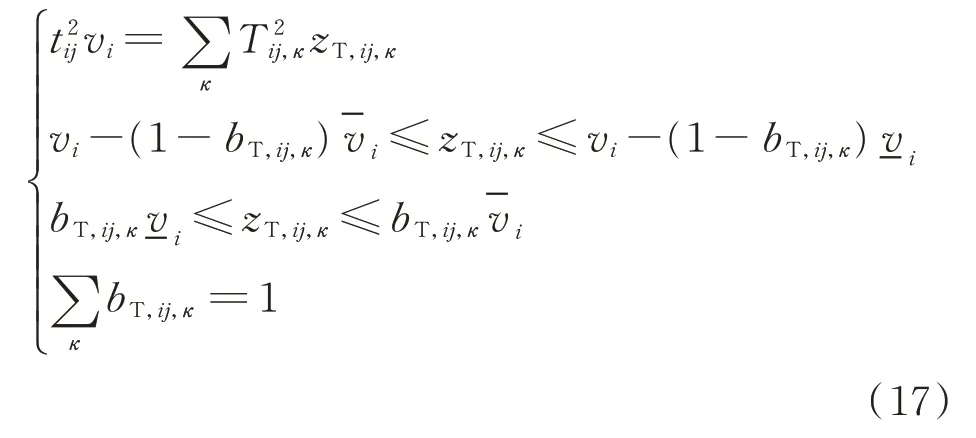
式中:zT,ij,κ為輔助變量。

2 兩階段魯棒優化模型

2.1 雙饋風力發電場提供無功支撐的策略

為使風電場向電網提供可靠的無功支撐,設計如圖1所示策略,它可分為3步。圖1中,x和y分別為第1階段和第2階段的優化變量。

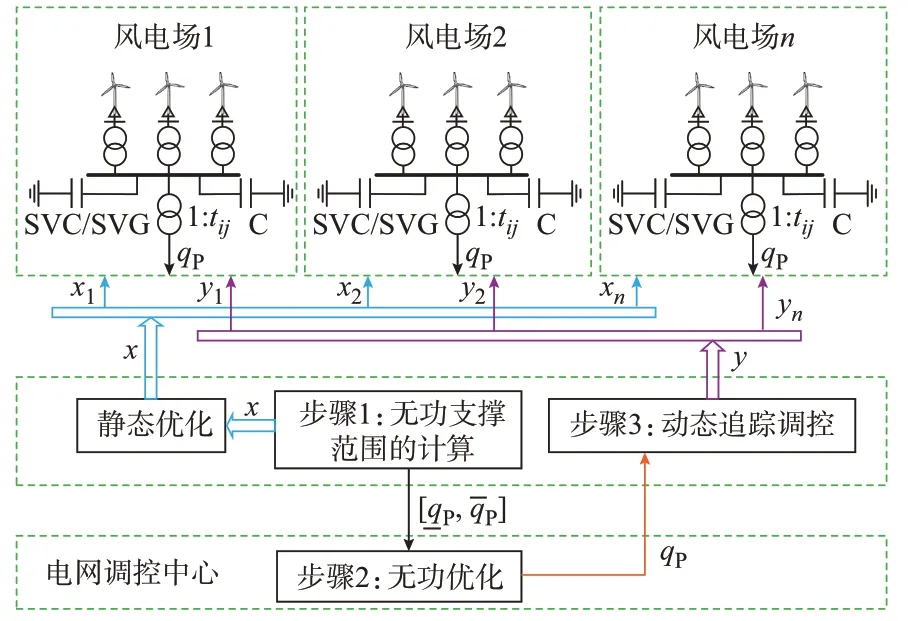
圖1 雙饋風力發電場為電網提供無功支撐的策略圖Fig.1 Strategy diagram of DFIG wind farms providing reactive power support for power grids

1）計算無功支撐范圍

風電場監控系統計算風電場無功支撐范圍,將它發送給電網調控中心。因為OLTC分接頭擋位調節和電容器組投切動作時限相對較長［18］,所以這一步驟中所確定的最優擋位和電容器組配置在后續動態追蹤調控時間段內（如10 min）保持不變。

2）電網無功優化

調控中心根據各風電場和其他調控資源的無功支撐范圍進行無功優化,確定包括PCC在內的各節點電壓設定值,并將無功需求發送給各風電場。

3）動態追蹤調控

根據調控中心下發的無功需求指令,風電場對DFIG和SVC/SVG等設備的無功功率進行調控以實現對電網無功需求指令的追蹤。

2.2 優化變量的分類

上述策略的第1步即本文研究內容。鑒于上述3個步驟的先后次序,并考慮不確定性影響,提出采用如下兩階段魯棒優化模型求取無功支撐范圍。

1）第1階段優化過程

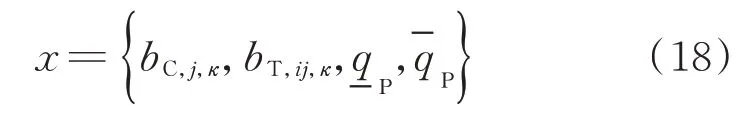
2）第2階段優化過程

第2階段用于判斷在給定的x下,對于不確定的DFIG有功功率和PCC電壓設定值的所有可能情況,風電場能否成功追蹤落在無功支撐范圍內的所有無功需求指令,以保證策略中第3步的可靠實施。因此,第2階段的優化變量包含無功輸出的控制 變 量qG,j和qS,j,風 電 場 的 狀 態 變 量vj、pij、qij、lij及輔助變量zC,j,κ和zT,ij,κ。定義第2階段優化變量集合y為:

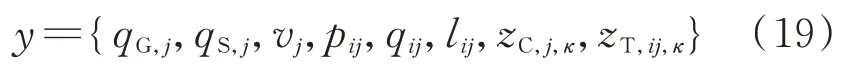
2.3 目標函數

目標函數是最大化風電場無功支撐范圍,即:

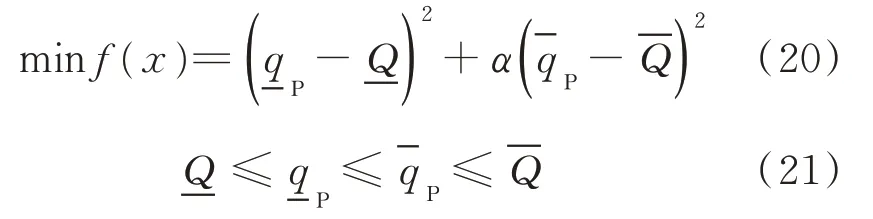
2.4 不確定集合

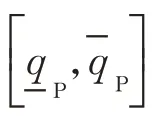
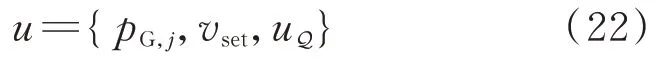
假設不確定集合為多面體集［19］,即:

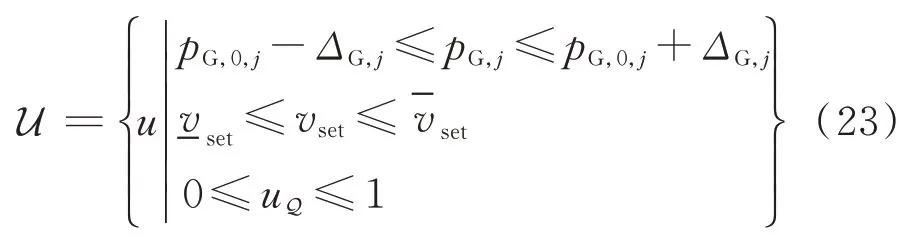
2.5 優化模型

目標函數式（20）,風電場運行約束式（1）至式（13）、式（15）、式（17）、式（21）和不確定集約束式（23）構成了求取雙饋風力發電場無功支撐范圍的兩階段魯棒優化模型,可進一步寫為如下數學形式（詳細對應關系請參見附錄B）:

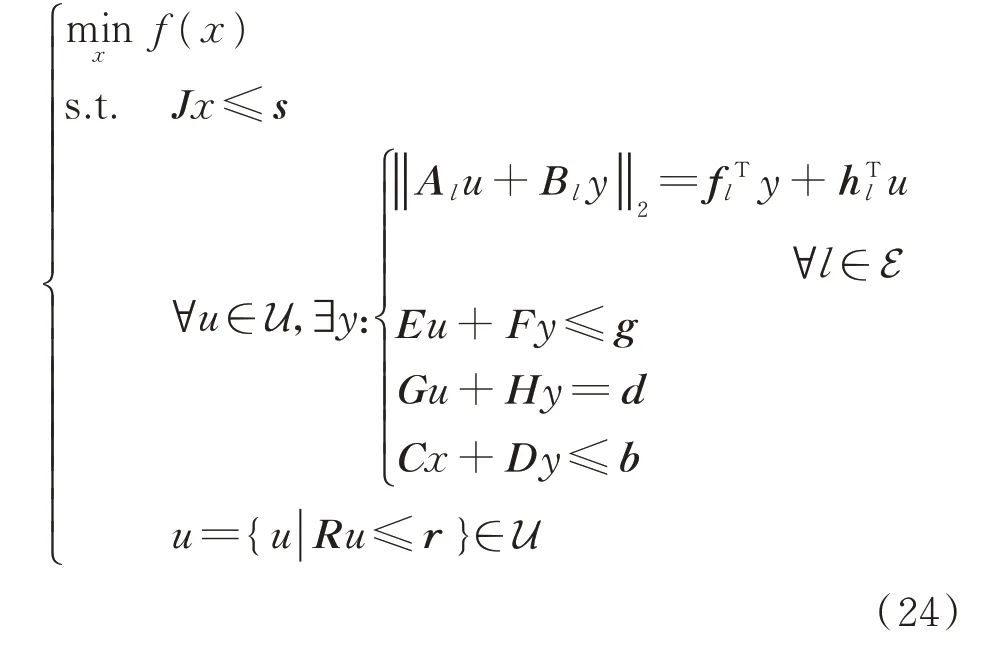
式中:Al、Bl、E、F、G、H、C、D、J、R為系數矩陣；fl、hl、g、d、b、s、r為系數向量；l表示線路集合E中的任一支路。

3 模型可解化處理

3.1 錐松弛

因式（24）的第2階段模型含有非線性等式約束,故其為非凸優化問題,難以求解。采用錐松弛方法將式（24）松弛為以下形式［12］:

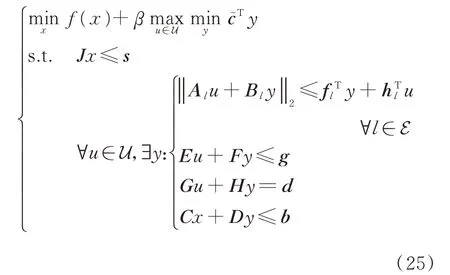
可將第2階段模型進一步寫為如下形式:

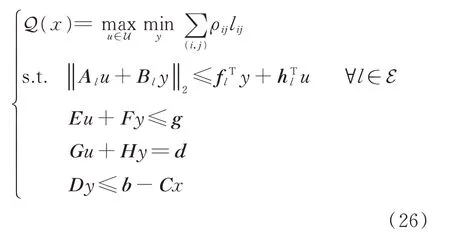
3.2 對偶轉化

式（26）中的目標函數為max-min結構,難以求解,采用對偶理論將其轉化為如下max-max優化模型:

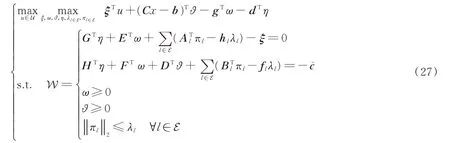
式中:η,ω,?為式（26）中線性約束的乘子；πl和λl為式（26）中錐約束的乘子；ξ為輔助變量；W為約束構成的集合域。

對式（27）目標函數中的雙線性項ξTu進行如下處理［12,20］。

1）因集合W和U不相交,可將目標函數進行如下等價轉換:

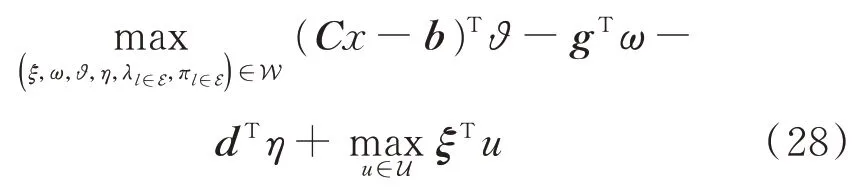
2）采用強對偶性定理,對雙線性項進行等價轉化,如式（29）所示。

式中:?為輔助變量,滿足以下約束條件

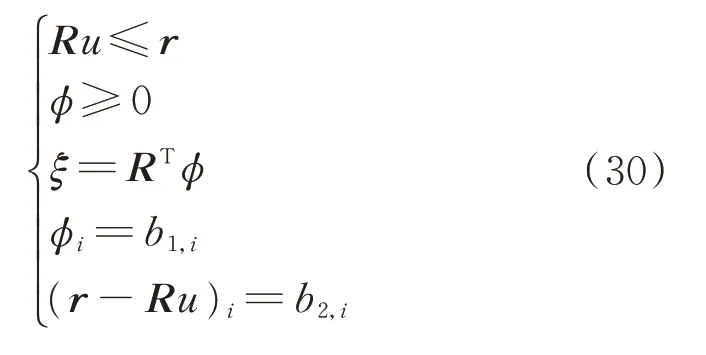
式中:b1,i和b2,i為輔助變量。

綜上,第2階段優化模型可以等價轉化為下述優化模型（其中變量b1,i、b2,i屬于第1類special ordered set,即SOS1）,進而可通過CPLEX或GUROBI等商用求解器直接求解。

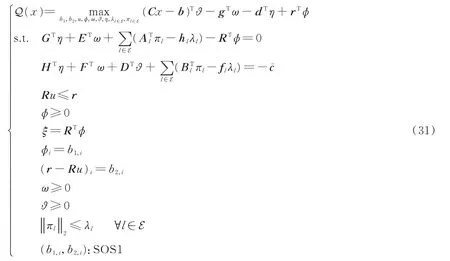
4 計算流程

圖2 基于列約束生成算法的模型求解流程圖Fig.2 Flow chart of model solution based on C&CG algorithm

5 無功支撐范圍的應用

5.1 電網的無功優化

在得到各個風電場無功支撐范圍后,電網將風電場作為無功源進行無功優化。目標函數為最小化網損。

電網無功優化模型中若沒有整數變量,可采用內點法［22］求解。若考慮并聯電容器組投切和OLTC分接頭擋位等離散變量,可采用臨近取整策略［23］、啟發式算法［24］或基于罰函數的算法［25］求解。由于很多文獻已詳述上述求解方法［22-26］,在此不再贅述。

當電網控制中心完成無功優化后,將得到PCC電壓幅值設定值和所需無功功率QD,將其發送給風電場監控系統以實現無功功率的動態追蹤。

5.2 風電場無功的動態追蹤

風電場在接收到電網控制中心發來的無功調度指令后,風電場監控系統對該指令進行動態追蹤。追蹤模型滿足約束式（1）至式（13）、式（15）、式（17）和式（21）:

目標函數式（32）將通過優化風電場DFIG和SVC/SVG無功功率來最小化風電場提供的無功功率和電網所需無功功率的差值。目標函數為0說明風電場可準確追蹤電網無功需求指令。因為γj,k和Tij,k的取值在無功支撐范圍估計步驟中已被確定,故在式（32）中為確定值,另外,DFIG有功輸出和PCC電壓幅值在式（32）中分別為預測值和電網下發的設定值。約束式（1）至式（13）、式（15）、式（17）和式（21）保證了風電場將在安全運行狀態下為電網提供所需的無功功率。

該優化模型為確定性的非線性問題,可使用內點法［22］高效求解。詳細求解過程不再贅述。

6 算例分析

6.1 算例系統

算例系統如圖3所示。其中,電網部分為IEEE 9節點算例系統,在節點5并入風電場［27］,對應的PCC電壓幅值上下限設置為［0.99,1.01］p.u.。其他數據可參見文獻［28］。

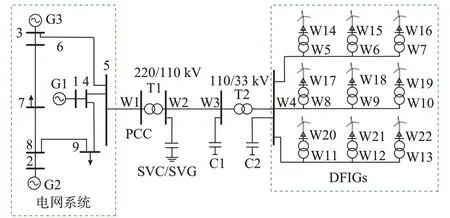
圖3 風電場并網系統Fig.3 Wind farm grid-connected system

風電場系統中共有6個DFIG,在線路W1-W2處的OLTC分接頭為5擋,變比調節范圍為±5×1%,線路W3-W4處OLTC變比設置為1。節點W2處安裝有一個SVC/SVG,其無功可調區間設置為［?2,2］Mvar。節點W3和節點W4皆安裝兩組可投切并聯電容器,每組容量為0.5 Mvar。PCC的電壓幅值上下限設置為［0.99,1.01］p.u.,無功功率上下限設置為［?100,100］Mvar,權重系數α設置為1,不確定性的DFIG輸出的有功基值設置為1.84 MW（考慮到同一風電場中風機有功預測和型號通常比較接近,為簡化仿真過程,本文假定風電機組參數均相同。但是從模型和算法部分易知,即使機組參數不同,本文方法仍然適用）。DFIG有功功率變化范圍設為0.2 MW。其他參數請見附錄C。仿真基于Matlab2014平臺,采用GUROBI求解器。計算機配置為intel i5-740,主頻3.0 GHz。

6.2 無功支撐范圍的計算

6.2.1 與線性疊加和確定性方法的對比

為說明計算風電場無功支撐范圍時考慮不確定性、離散性和非線性因素的必要性,對比如下3種方法。

方法1:文獻［3-5］中的線性疊加法,所有DFIG和SVC/SVG的無功容量疊加,但不考慮電容器和OLTC變比的調節,即忽略不確定性、網絡約束和離散變量,則風電場無功支撐范圍為:

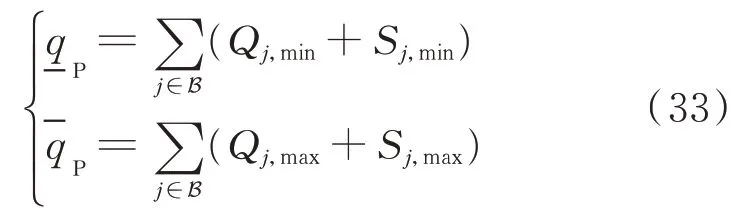
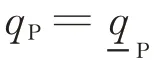
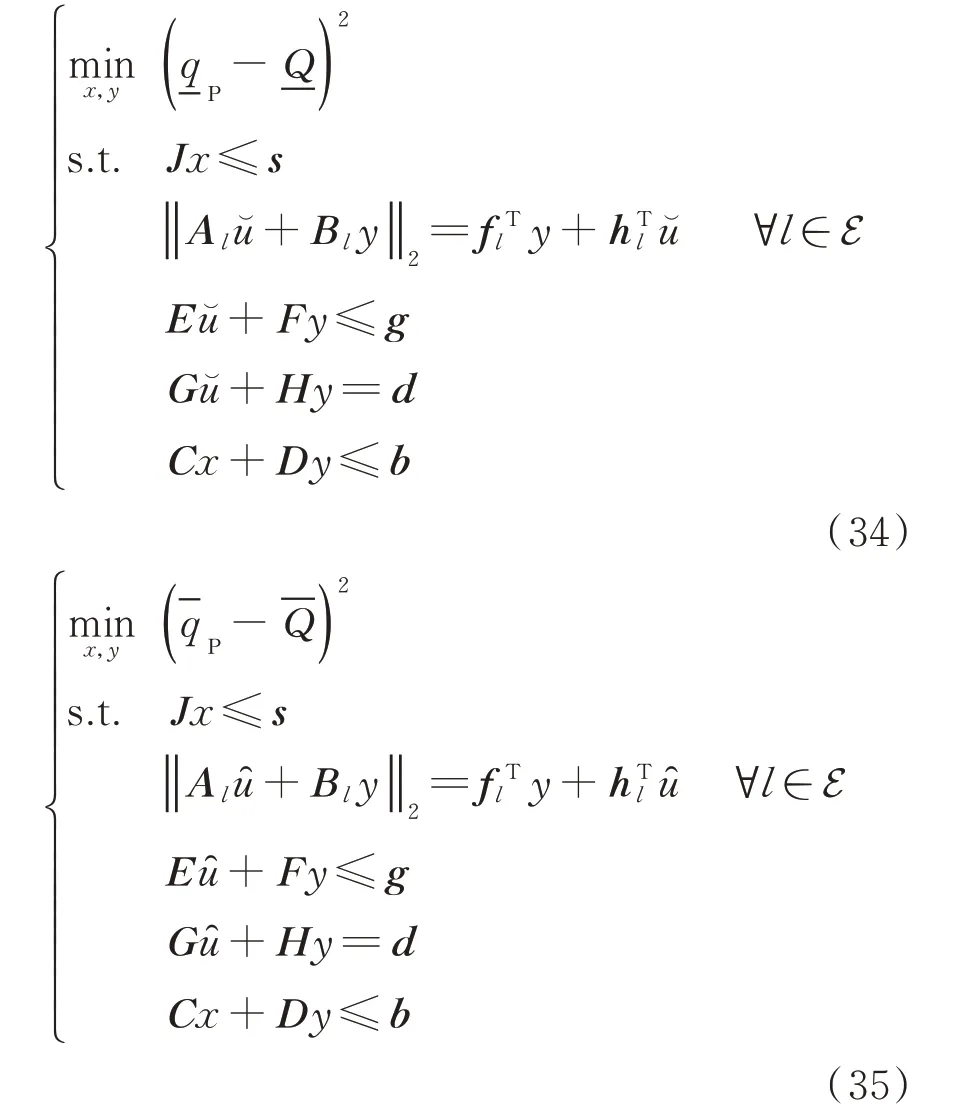
方法3:本文方法,同時考慮不確定性、網絡約束和離散變量。

3種方法計算結果如表1所示。

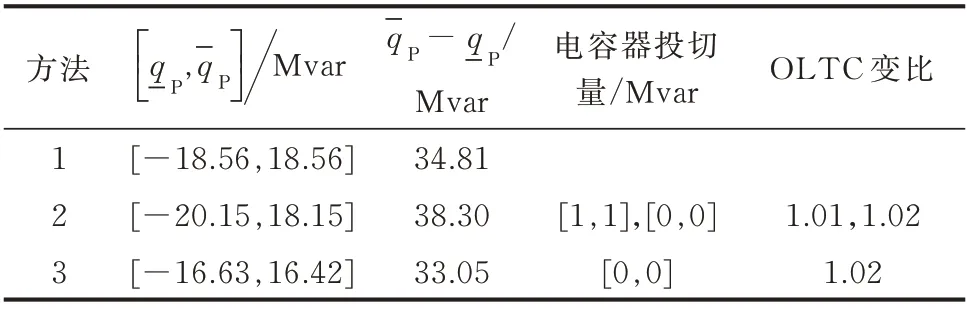
表1 3種方法結果對比Table 1 Result comparison of three methods

從表1中方法1和方法3的對比可見,本文方法較文獻［3-5］方法得到的無功支撐范圍小。原因在于本文方法考慮了包括DFIG有功功率在內的不確定性以及網絡約束、線路容量和電壓幅值等因素的影響。在實際應用中,若采用文獻［3-5］方法求得的無功支撐范圍,部分無功功率值可能在實際中無法獲得（如±18.56 Mvar）,即高估了不確定環境下風電場的無功支撐能力。因此,相較于文獻［3-5］中的方法,本文方法更加準確。

從表1中方法2和方法3的對比可以看出,相較于確定性方法,本文方法所得無功支撐范圍較小。因為方法2同樣未能考慮不確定性的影響,且其求得的無功支撐范圍上下限所對應的并聯電容器組的投切量與OLTC分接頭擋位的配置不同（如［1,1］和［0,0］）。在實際應用中,OLTC分接頭擋位調節和電容器組投切的動作時限較長,無法實現對所求無功支撐范圍內無功功率的動態追蹤。本文方法中,OLTC分接頭擋位調節和電容器容量已優化配置為確定值,符合實際需求,并考慮了不確性的影響。

綜上,相較于方法1和方法2,本文方法充分考慮了風電場中的不確定性等實際因素,能夠準確地計算風電場無功支撐范圍。

6.2.2 目標函數中權重系數的影響

將權重系數α分別設置為0.5、1和1.5,計算風電場的無功支撐范圍,結果如表2所示。

表2 權重系數的影響Table 2 I mpact of weight coefficient

由表2可知,當α等于0.5時,所求無功支撐范圍的中點更小。這意味著當α較小時,無功支撐范圍傾向于提供容性無功功率；反之相反。此外,當α等于1.0和1.5時,無功支撐范圍相同。這是因為當α等于1時風電場用于輸出感性無功功率的調節手段已用盡。如表2所示,當α等于1時,電容器投切量為0,OLTC變比與α等于1.5時相同,且DFIG和SVG/SVG輸出無功功率也已達到極限,故無功支撐范圍不再變化。

綜上可知,調節權重系數可滿足電網的不同無功需求,但調節范圍會受到風電場內部可調設備調節裕度的限制。

6.2.3 計算效率

表3列出了幾種不確定場景下計算風電場無功支撐范圍所需時間和迭代次數等信息。

從表3中可見:①在所測示例中,算法均可在有限的迭代次數內收斂；②隨著不確定性增強,單次迭代平均用時呈增加的趨勢；③計算所用時間最多為24.44 s,遠小于常見調度間隔（如10 min）,可滿足實時調度的時間要求。此外,上述試驗都運行于個人筆記本計算機,如果采用高性能計算服務器,計算時間會進一步降低。

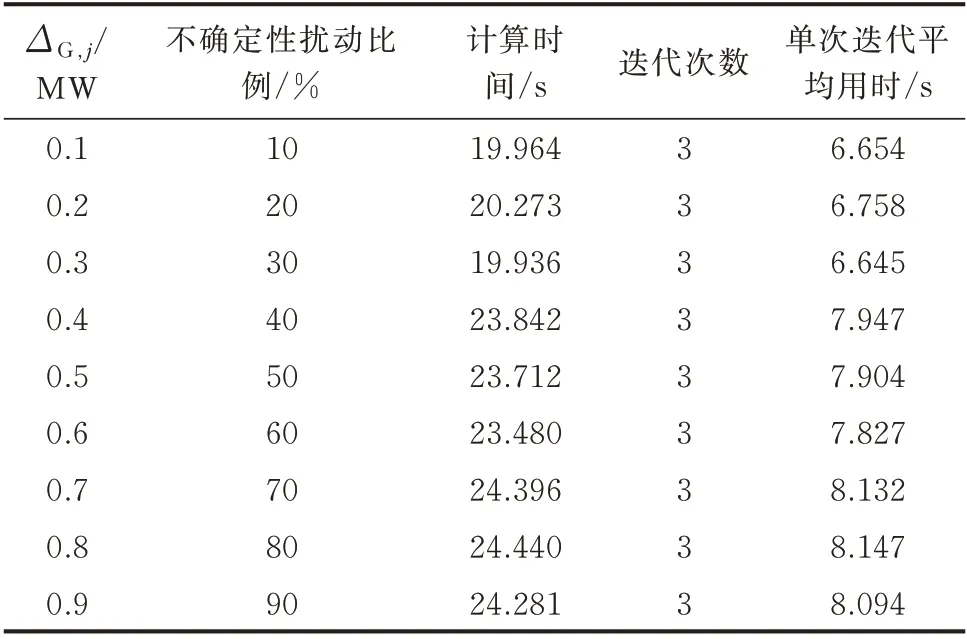
表3 不同不確定性場景下的計算時間Table 3 C omputation time in different uncertain scenarios

6.3 風電場無功支撐范圍的應用

采用圖3中的算例系統,進行如下3個步驟。

步驟1:無功支撐范圍的計算。

風電場無功支撐范圍由本文所提無功支撐范圍方法計算,為［?16.63,16.42］Mvar,風電場監控系統將該值發送給電網控制中心。同時,風電場內部并聯電容器組和OLTC分接頭因存在投切時限,故在此分別被確定為［0,0］Mvar和1.02,其值將在一段時間內保持不變。

步驟2:電網的無功優化。

電網控制中心在接到風電場監控系統發來的無功支撐范圍后,進行電網無功優化。最優網損值為1.89 MW,其他優化結果如表4所示。從中可見,風電場從電網提供吸收總的無功為16.42 Mvar,PCC電壓幅值為1.01 p.u.,將其發送給風電場監控系統。

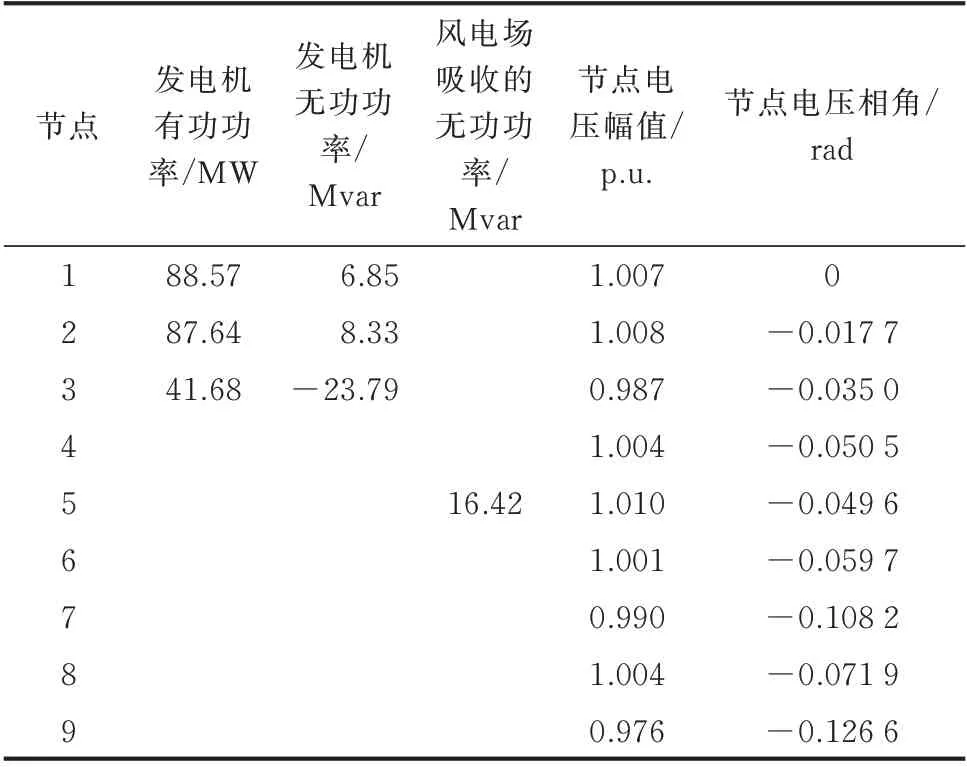
表4 步驟2的優化結果Table 4 O ptimization results of step 2

步驟3:無功功率功率的動態追蹤。

風電場接收到電網控制中心點指令后,采用上述5.2節中的方法對無功指令進行動態追蹤。目標函數的值為0,表明風電場可以精確度追蹤電網所需無功。其他優化結果如表5所示。

表5 步驟3的優化結果Table 5 O ptimization results of step 3

至此,通過無功支撐范圍的計算、電網無功優化和無功功率動態追蹤這3個步驟實現了風電場作為無功源參與電網無功優化的過程。

6.4 與傳統方法對比

為探究風電場作為無功源參與電網無功優化的優勢,與風電場不作為無功源的傳統無功優化方法進行對比。因為傳統方法中PCC處無功功率不可調,相當于無功負載,分別設置其為?15,?5,0,10 Mvar進行仿真,電網無功優化結果如表6所示。從中可知,相較于傳統方法,風電場作為無功源參與電網優化可降低網損,這是因為風電場作為無功源相當于增加了電網的控制手段。

表6 電網無功優化結果Table 6 O ptimization of reactive power in power grid

7 結語

本文提出基于兩階段魯棒優化的風電場無功支撐范圍計算方法。相較于線性疊加方法和確定性方法,本文方法考慮了不確定性、網絡約束和離散變量對無功支撐范圍的影響。理論和算例分析表明,相較于其他方法,所提出的魯棒估計方法能夠準確計算風電場無功支撐范圍。算法收斂性和計算效率也在算例分析中得到驗證,可滿足現場需求。另外,本文給出了風電場作為無功源參與電網無功優化的策略,算例分析表明利用風電場無功支撐范圍可以有效降低系統網損。

在后續研究工作中將進一步考慮更加精細的風力機模型。此外,本文中基于風電場無功支撐范圍的電網無功優化模型為確定性模型,但實際電網也可能面臨其他不確定因素,對此需探究相應的模型和算法工具。