基于非線性規劃的中近距空空導彈增程彈道設計方法

王 龍，李 斌

(中國空空導彈研究院，河南洛陽 471000)

0 引言

在實際空戰條件下，“先敵發現、先敵發射、先敵命中、先敵脫離”是飛行員能夠制勝的“四先”準則，追求射程的不斷提高是空空導彈不變的發展方向之一[1-2]。在導彈發動機推力和阻力特性確定的條件下，導彈的最大發射距離取決于實際的飛行彈道。因此，增程彈道設計是能夠讓飛行員實現“先敵發射”的一項關鍵技術。在工程應用中，傳統的空空導彈增程彈道設計方法是先確定一種彈道方案，然后基于仿真數據對彈道方案中的相關參數進行調試和設計[3]。該方法在一些彈道條件下能獲得較好的性能，但由于空戰環境復雜多樣，通過離線仿真設計的參數難以適應所有彈道條件。為了避免導彈攻擊區出現漏洞，通常需要進行大量的仿真并對參數進行反復修正，效率較低。

彈道設計本質上屬于非線性優化問題，針對該類問題目前常用的理論方法有間接法和直接法。間接法是將優化問題轉化為兩點邊值問題進行求解，對初值精度要求高，選取不當可能無法得到計算結果，且求解過程比較復雜，因此在復雜彈道設計問題上的應用頗受局限[4]。直接法是將連續的優化問題進行參數轉化，然后再通過合適的方法進行求解。常用的直接法主要有直接打靶法[5]、多重打靶法[6]、配點法[7]、微分包含法[8]等。目前配點法中的偽譜法已成為軌跡優化問題的主流方法。該方法的特點是在時間節點上通過插值多項式對控制變量和狀態變量進行近似，并將微分方程約束轉化為代數約束，然后通過常規的方法進行求解[9]。偽譜法的最大優點是對初值不敏感、收斂較快且計算精度高，因此在航天飛行器的軌跡優化上已得到了廣泛應用[10-15]。

空空導彈飛行時間短，飛行過程中推力和質量時變，升阻比系數小，大氣參數依賴導彈的飛行高度，且要攻擊空中運動目標，因此空空導彈的增程彈道設計是一類復雜的時變動態規劃問題。鑒于偽譜法的諸多優勢，文中首先基于偽譜法將空空導彈的增程彈道設計問題進行參數化描述，轉化為一般的非線性規劃問題進行求解，然后給出求解方法。

1 空空導彈增程彈道設計問題描述

1.1 運動模型

1.1.1 導彈運動模型

對于空空導彈，其在彈道坐標系下的三自由度運動模型為：

(1)

式中：xm、ym、zm為導彈在慣性坐標系下的坐標；vm為導彈速度大小；θm、ψm分別為導彈的彈道傾角和彈道偏角；m為導彈質量；ms為發動機的燃燒速率；P為導彈發動機推力；X、Y、Z分別為氣動阻力、升力和側向力；α、β分別為導彈的攻角和側滑角。

1.1.2 目標運動模型

目標運動模型為:

(2)

式中:xT、yT、zT為目標在慣性坐標系下的坐標；vT為目標速度大小；θT、ψT分別為目標的速度俯仰角和方位角；nθT和nψT分別為目標的俯仰機動過載和方位機動過載；nT為目標機動過載大小。

1.2 空空導彈增程彈道設計問題描述

1.2.1 約束條件

空空導彈在飛行過程中受到的約束主要有推力約束、質量約束、控制輸入約束以及終端約束等。

1)推力約束

中近距空空導彈的發動機通常為一級，推力的約束形式為：

(3)

式中:P0為導彈發動機推力大小;t1為導彈發動機的工作時間。

2)質量約束

在主動段，導彈的質量隨著發動機燃料的燃燒減小；在被動段，導彈的質量保持不變，因此導彈的質量約束為：

(4)

式中，ms0為發動機的秒消耗量。

3)控制輸入約束

在三自由度模型中，導彈的控制輸入為攻角和側滑角，其約束條件為:

(5)

式中，αmax、βmax分別為攻角和側滑角的最大值。

4)終端狀態約束

設導彈可容許脫靶量的最大值為Rmax，則導彈的終端約束為:

(6)

1.2.2 增程彈道設計問題描述

對于空空導彈，在評估其射程指標時一般以一定速度作為截止條件。在實際作戰時，空空導彈的實際射程取決于發射時刻的彈-目相對距離，設計空空導彈的攔截彈道時可以將末速大小作為指標，因此增程彈道設計問題可描述為：

(7)

其中，tf為終端時刻，動態微分方程約束為式 (1)和式(2)。

2 基于非線性規劃的空空導彈增程彈道設計

下面基于偽譜法對彈道設計問題進行參數化描述，然后給出彈道設計的求解算法。

2.1 基于偽譜法的彈道設計問題參數化描述

2.1.1 微分方程的參數化

(8)

其中，u=[αβ]T。

將時間區間[t0,tf]轉換到[-1,1]，引入時間變量τ，其定義為：

(9)

插值時間節點是時間區間[-1,1]內的N階Legendre多項式P(τ)的根，其中P(τ)可表示為：

(10)

通過求取[-1,1]內的N個Legendre-Gauss插值點τ1,τ2,…,τN，則系統在τ1,τ2,…,τN處狀態值的Lagrange插值多項式為:

(11)

式中，Li(τ)為插值基函數，其表達式為:

(12)

同理，系統在τ1,τ2,…,τN處控制輸入的Lagrange插值多項式為:

(13)

(14)

由于τ1,τ2,…,τN處的狀態變量和控制輸入是式(11)和式(13)的參數，因此需要將運動模型參數化，從而轉化為關于τ1,τ2,…,τN處狀態變量和控制輸入的代數約束。

對式(11)求關于時間的導數，可得:

(15)

(16)

在τk時刻，根據式(8)、式(11)、式(15)可得:

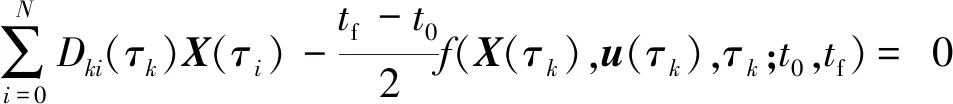
(17)

2.1.2 約束條件參數化

推力約束的參數化可描述為：

(18)

質量參數化可描述為：

(19)

輸入約束的參數化可描述為:

(20)

為了描述終端約束，首先需要對終端狀態進行參數化描述。根據運動模型，終端狀態可描述為：

(21)

對于積分函數，可采用N個插值點的求積進行近似，即

(22)

式中wi可表示為：

(23)

于是，終端約束為:

(24)

2.1.3 指標函數參數化

指標函數的參數化描述為：

(25)

其中，vm(τf)可通過式(21)進行求解。

通過參數化描述，可將連續的無限維彈道優化問題轉換為一般的非線性規劃問題，即在上述參數化約束條件下，求取[t0tf]時間段內的狀態變量Xk(k=1,2,…,N)、輸入變量uk(k=1,2,…,N)以及終端時刻tf使得導彈終端速度最大。

2.2 彈道優化問題的求解算法

彈道設計問題通過參數描述之后轉換為多約束下的非線性規劃問題，下面基于序列二次規劃給出求解算法。

以式(25)為優化指標，以Xk(k=1,2,…,N)、uk(k=1,2,…,N)為優化變量，以式(17)～式(19)為等式約束，以式(20)、式(24)為不等式約束的非線性規劃問題可描述為：

(26)

定義拉格朗日函數：

(27)

式中，λ=[λ1,λ2,…,λNeq,λNeq+1,…,λNeq+Nieq]為拉格朗日乘子系數。

下面給出非線性規劃問題式(26)的求解算法。首先，求解如下的二次規劃問題：

(28)

然后，通過求解如下的優化問題得到迭代步長αk：

(29)

最后，根據迭代方向dk和迭代步長αk更新狀態向量：

(30)

3 仿真驗證

下面通過仿真來驗證文中空空導彈彈道設計方法的有效性。

3.1 仿真條件設置

假設某型空空導彈相關參數如表1所示。

表1 某型空空導彈相關參數

假設導彈發射時刻載機和目標運動參數如表2所示。

表2 載機和目標初始運動參數

3.2 仿真結果

仿真計算得到的導彈運動狀態和控制輸入如圖1～圖4所示。圖1為導彈在垂直方向上的運動軌跡，圖2和圖3分別為導彈的速度大小和彈道傾角曲線，圖4為導彈的攻角和側滑角輸入曲線。根據圖1可知，導彈的最優軌跡為高拋彈道，即爬升到高空利用空氣阻力小的優勢減小導彈的速度衰減率，從而達到提高末速的目的，導彈的最大高度為16 215.4 m。圖2中實線為文中方法的導彈速度曲線，虛線為比例導引下的導彈速度曲線，仿真結果表明，文中方法下導彈的末速大小為323.2 m/s，比例導引下導彈的末速大小為216.3 m/s，文中方法的彈道末速比比例導引大106.9 m/s。若將323.2 m/s作為彈道仿真的截止條件，通過二分法計算得到比例導引下導彈能夠命中目標的最大發射距離為30.6 km，比文中彈道設計方法的發射距離小了9.4 km，從而驗證了文中彈道設計方法能夠大幅提升導彈的最大發射距離。初始發射距離為30.6 km時，比例導引下的導彈速度隨時間的變化曲線如圖5所示。

圖1 導彈和目標垂直運動軌跡

圖3 導彈彈道傾角

圖4 導彈控制輸入

圖5 比例導引下的導彈速度曲線(發射距離30.6 km)

4 結論

以近距空空導彈為對象，考慮作戰過程中的實際約束條件，以導彈最大末速為指標，建立了空空導彈彈道設計問題的數學描述，基于偽譜法對彈道設計問題進行參數化描述，然后給出了求解算法，并通過數字仿真進行了驗證。仿真結果表明，在給定初始發射條件下，該彈道設計方法能夠顯著提高導彈的末速，且計算精度較高。基于文中的彈道設計方法，在相同末速限制條件下，能夠提高導彈的最大發射距離，使載機能夠做到先敵發射，從而提高導彈的作戰能力。