基于線性互補問題的多體系統接觸/碰撞動力學研究

張欣剛，齊朝暉，王 剛，國樹東，吳志剛

(1. 青島理工大學 理學院，青島 266525; 2. 大連理工大學 工業裝備結構分析國家重點實驗室，遼寧 大連 116024;3. 大連理工大學 海洋科學與技術學院，遼寧 盤錦 124221)

隨著智能機器人、航空航天等領域的發展，輕質化、柔性化、復雜化、快速化的機械系統得到了廣泛的使用，同時也促進了多柔體系統動力學學科的蓬勃發展[1]。以航天科技為例，其空間結構往往以折疊狀態固定在艙內，入軌后再逐步展開，如大型桁架式索網天線，大型太陽能電池陣,柔性抓取機械臂等[2]。為了控制航天器的重量，這些結構多為大型輕質柔性結構。這些柔性構件在展開過程中不僅呈現出大轉動、大變形剛柔耦合的動力學特性，其部件也不可避免的要與周圍環境或自身發生接觸/碰撞[3]，由此產生的非光滑振動不僅給航天器的姿態控制帶來較大的困難，甚至導致航天器的失穩[4]。因此，深入分析結構柔性以及碰撞、摩擦對系統動力學特性的影響具有切實的意義。

對碰撞的描述可分為兩類：① 忽略碰撞的細節，認為碰撞在瞬間完成[5-7]；② 用彈簧模擬物體對變形的抵抗能力，用阻尼模擬能量耗散[8-10]。第一類方法又被稱為離散分析方法，優點是簡化了接觸過程且計算效率高，缺點在于不能計算碰撞過程中碰撞力的大小以及作用過程，其線性補償策略可能會違反摩擦接觸時的能量守恒定律[11]。第二類方法又被稱為連續分析方法，允許接觸體在接觸區域相互嵌入，接觸力可表示為侵入量的明確函數[12]。其中Hertz接觸理論是使用范圍最廣研究范圍最悠久的接觸力模型。文獻[13]系統總結了Hertz接觸模型的發展，并著重討論了模型中阻尼系數的發展過程。

將多剛體系統中應用最為廣泛的連續接觸力模型直接引入到多柔體接觸/碰撞動力學分析中并非完全適用[14]。連續接觸力模型將接觸力描述為變形量的明確函數，相當于引入一個本構關系。而柔體自身有其本構關系。引入連續接觸力模型刻畫柔體間的碰撞，相當于給系統疊加了本構關系，從而使得兩者相互干擾：一方面，模型中剛度和阻尼參數的確定含有很大的不確定性[15-17]；另一方面，由于一次碰撞歷程中相對速度可在較大的范圍內取值，加之受到兩類本構關系的干擾，往往會計算出負的接觸力，從而與接觸力的性質相違背。基于線性互補理論的非光滑動力學模型能夠保證接觸力的非負性，且能夠高精度的求解持續接觸狀態下的接觸力，不足之處在于需要區分不同的接觸狀態，且無法同時定性和定量的分析碰撞時刻的接觸力演化過程[18]。

結合以上研究現狀，本文首先分析了連續接觸力模型在多柔體接觸/碰撞分析中的不足，隨后在非光滑動力學的體系下，將多柔體系統模型降噪[19]的思想引入柔體間動態接觸力的建模與計算當中，建立了平均化縫隙與接觸力之間的標準線性互補方程。這種互補關系可以綜合考慮碰撞和平順接觸，在接觸狀態發生改變時不需切換模型。不僅保證了接觸力的非負性，也在很大程度上簡化了非光滑互補問題的分析和求解過程。

1 柔體間動態接觸力模型

1.1 連續化模型

接觸力可視為單面約束提供的約束反力，其重要力學特性是約束反力的單向性：沿縫隙函數gi增加方向的接觸力值τi必須非負，而當縫隙函數gi大于零時τi必須為零。因此縫隙函數和法向接觸力必然滿足以下關系式

0≤gi⊥τi≥0

(1)

盡管上述關系符合客觀事實，但由于縫隙函數本身與接觸力并不存在明確的函數關系，因此我們僅能通過它定性的確定接觸力是否為零，而難以確定其幅值。

為了刻畫柔體間碰撞力的演化過程，一些學者將連續接觸力引入到柔性多體系統接觸/碰撞動力學中，例如應用很廣泛的Lankarani和Nikravesh模型

(2)

式(1)的一個特例是，當單面約束正在起作用時，由于縫隙函數及其一階變化率均為零，因此退化為平順接觸時的線性互補關系

(3)

由動力學普遍原理可知，縫隙函數的二階變化率與接觸力存在函數關系，因此接觸力可以被確定，大量算例也證實了這種關系的真實性。由此可見，平順接觸條件下不需人為設定接觸力模型也可以高精度的求解接觸力。事實上，連續接觸力模型將圖1(a)物體之間的瞬時碰撞抽象為圖1(b)所示的等效系統。由圖1可見，人為設定柔體之間的接觸力模型相當于給系統疊加兩個本構關系，從而帶來了一定程度的干擾。

(a)

(b)圖1 柔體間接觸力模型Fig.1 Contact force model between two flexible bodies

1.2 互補問題的光滑化方法

類比庫倫摩擦定律可見：一些物理上正確的數學描述往往無法用于數值分析。當所研究的系統無stick-slip運動狀態的切換時，人們往往采用修正的庫倫摩擦模型來代替。將間斷函數連續化也是處理非光滑問題的一類被驗證可行的方法。

類似地，將縫隙函數在短時間[t,t+h]內做泰勒展開，并保留到2階,則ξ時刻的縫隙函數可表示為

(4)

(5)

由此可將接觸力與縫隙函數的互補關系近似為

(6)

由于平均化縫隙函數表達式(5)中含有縫隙函數二階變化率項，因此可確定接觸力。經此近似以后的互補方程可以綜合考慮接觸與碰撞，且不必將接觸過程人為的劃分為多個狀態。與式(6)等價的非線性方程形式為

(7)

2 接觸/碰撞的線性互補方程

建立均勻化縫隙與接觸力之間的標準線性互補方程，還需推導縫隙加速度與廣義加速度之間以及廣義加速度與接觸力之間的函數關系。建立多柔體系統動力學方程的物理依據是虛功率原理，可表述為彈性體外力虛功率等于彈性體慣性力虛功率與彈性體變形虛功率之和

(8)

式中：r為物體內一點的矢徑；σ和ε分別為該點處的廣義應力和廣義應變；f為作用在該點的外力。當給系統增加外力時，僅需計算該作用力的虛功率并疊加到系統虛功率方程中即可。

不考慮接觸力時，系統的虛功率方程可由廣義坐標q表示為

(9)

式中:M為廣義質量陣;F為廣義力陣。

接觸力的虛功率可表示為

(10)

將接觸點虛速度用廣義速度表示，則式(10)可改寫為

(11)

(12)

所有接觸力虛功率之和為

(13)

式中

Kf=[Tf1e1,Tf2e2,…,Tfnen]

(14)

f=[f1,f2,…,fn]T

(15)

接觸力對廣義力的貢獻即為Kff，如果式(9)所選的廣義坐標獨立，則系統動力學方程可由此寫為

(16)

由式(16)，可將廣義加速度由接觸力線性表示

(17)

根據運動學關系，我們也總能將縫隙函數的變化率表示為廣義坐標變化率的函數

(18)

(19)

綜合式(7)以及式(17)～(19),并將其代入式(5),我們可以通過標準線性互補問題

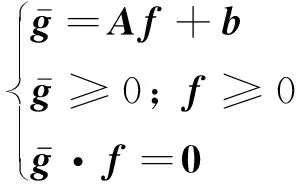
(20)

并通過求解其等價的非線性方程組(7)來求解接觸力f，其中

(21)

(22)

求解式(20)得到接觸力后，代入式(17)即可得到廣義加速度。

用均勻化的縫隙函數與法向接觸力建立互補方程，實際上是將突變的接觸力進行了光滑化處理，當物體臨近接觸時接觸力已經開始起作用，而當縫隙函數及其變化率均為零時，方程又可退化為平順接觸時的接觸力方程。一方面能夠解出接觸力隨時間的演化，另一方面嚴格滿足互補條件，因此不會解出負接觸力。

3 數值算例

例1：圖2所示的彈性質量系統，各質量點均為mi=m=1 kg，彈簧剛度ki=k=104N/m。靜止狀態下間隙為零。左側3號質點在外力作用下向左移動0.03 m，達到靜平衡后釋放并與右側系統發生碰撞。分別采用彈簧阻尼模型以及所提線性互補方法進行數值仿真。彈性阻尼模型的等效剛度取140×106N/m3/2。

圖2 彈簧質量系統Fig.2 Spring-mass system

為了進一步討論連續接觸力模型對柔體本構關系的影響，我們以Flores模型為例，分別計算不同恢復系數條件下的系統響應。圖3分別給出了不同恢復系數、相同時刻不同恢復系數兩種情況下的系統機械能時程曲線，圖中cr表示恢復系數。

由圖3(a)可見，恢復系數為1時為純彈性碰撞，系統機械能守恒。但隨著恢復系數的降低，在相同時刻，系統機械能并沒有隨著恢復系數的降低而降低，而是呈現一定的波動。圖3(b)給出了相同時刻不同恢復系數條件下系統機械能的變化,更為直觀了展示了這種波動。

除以上情況外，計算得到的恢復系數與預設的恢復系數也呈現了較大的差異，圖4給出了不同接觸力模型設定恢復系數與計算恢復系數的比較。

(a) 時程曲線

(b) 相同時刻不同恢復系數圖3 系統機械能Fig.3 System energy

圖4 預設與計算恢復系數關系Fig.4 Relation between the post and pre-restitution coefficients

對比圖4以及文獻[8]可見，Flores模型在計算剛體間碰撞時恢復系數與預設值吻合較好，但計算柔體間碰撞時就產生了較大的偏差。其余兩種經典接觸力模型[9,10]在計算剛體間高恢復系數碰撞問題時吻合較好，但計算柔體碰撞時也產生了一定的偏差。

除了以上兩種情況外，將接觸力模型引入到柔體間接觸問題往往得到負的接觸力。其主要源于兩個方面：① 相對速度可在較大范圍內取值；② 阻尼項中分母若含有恢復系數，則在低恢復系數時阻尼項絕對值被放大。如圖5所示。其中各接觸力模型及其適用范圍可參照文獻[20]的歸納總結。

由圖5可見，對于分母中含有恢復系數的遲滯阻尼因子，在低恢復系數下其幅值就會被放大，加之相對速度在較大范圍內取值，在低恢復系數情況下很容易計算出小于負1的阻尼項，如圖6所示(Flores模型)。一次碰撞過程中接觸力與侵入深度的關系如圖7所示。當物體間相對速度為正(脫離)時，相對速度與初始相對速度之商為負，由于模型中阻尼項系數被分母中的恢復系數放大，則在物體脫離對方的時刻計算出了如圖7所示的負接觸力。

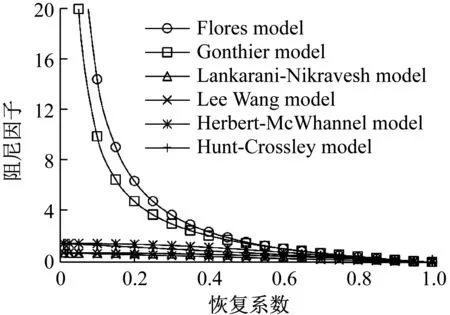
圖5 阻尼因子與恢復系數關系Fig.5 Relation between damping factor and restitution coefficients

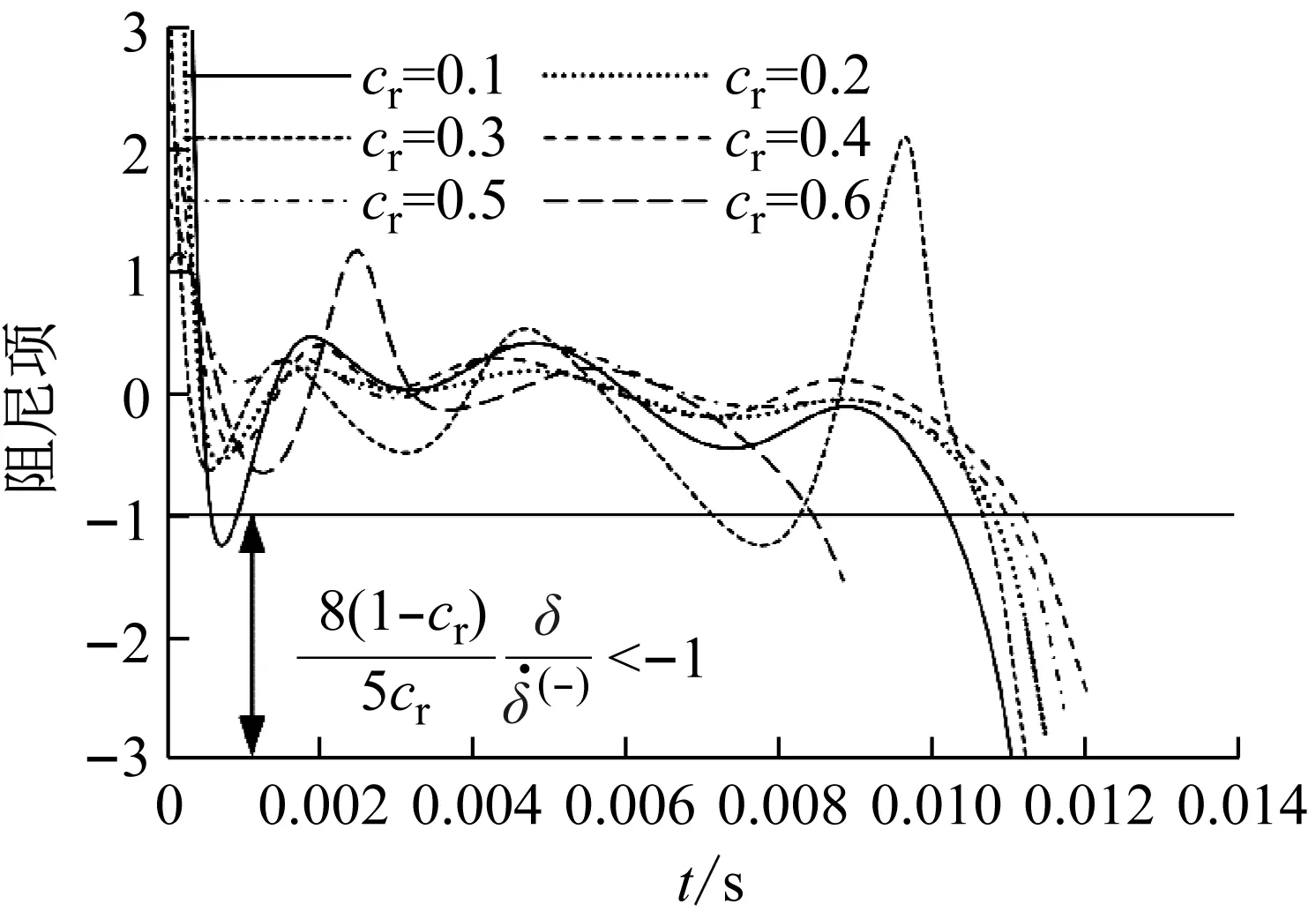
圖6 阻尼項時程曲線Fig.6 Time plot of damping item

圖7 接觸力/嵌入量關系Fig.7 Contact force-deformation relation

采用所提線性互補方法時，實際縫隙函數與均勻化縫隙函數的關系如圖8所示。由均勻化縫隙函數的表達式(5)可知，物體相互靠近時，縫隙函數大于零，其一階變化率小于零，因此均勻化縫隙比真實縫隙要小一些，則在物體實際碰撞前的一個較短時間內接觸力已經開始作用。并且h值越大，接觸力作用的時間越早，接觸力的峰值也隨之降低。如圖9所示。

圖8 縫隙函數與均勻化縫隙函數關系Fig.8 Relation between normal gap and time-averaged gap

圖9 不同參數h下的接觸力時程曲線Fig.9 Time lapse of contact force with different h

圖10給出了圖9相應的接觸力與實際縫隙函數的關系。與連續接觸力模型相似，兩者均可視為局部碰撞的連續化。但由于采用均勻化縫隙與接觸力建立互補關系，因此物體在發生碰撞時也會有一定的嵌入量。另外，與沖量形式的摩擦碰撞線性互補模型[21-23]相比，優點在于可直接求解接觸力的大小，且碰撞前后的狀態依賴于柔體自身的本構關系，不必人為的設定沖量恢復系數。

圖10 接觸力與縫隙函數的關系Fig.10 Contact force-gap relation

縫隙函數均勻化區間長度h對系統動力學響應以及接觸力有著很大的影響，圖11給出了不同光滑參數h下滑塊3的位移時程曲線。

結合圖11以及圖9可見，均勻化區間長度h取值越大，接觸力作用時間越長，碰撞效應將被磨平，位移曲線較為光滑。隨著h值的減小，位移曲線逐漸吻合，更趨近于真實響應，但過低的h值也會使得所求接觸力失真。建議h的取值應與碰撞時間在相同數量級。

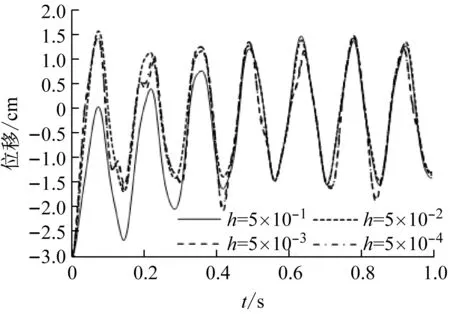
圖11 滑塊3位移時程曲線Fig.11 Time lapse of the displacement of slider 3

實際上，除了碰撞力本身外，人們更為關心的是碰撞前后系統的動力學行為。圖12給出了分別采用所提LCP方法以及連續接觸力模型(CCF)計算的滑塊3位移時程曲線以及接觸力時程曲線，其中連續接觸力模型中恢復系數取0.3。從中可見，除了連續接觸力模型會計算出負接觸力外，兩種模型所求接觸力略有差異，但系統動力學響應基本吻合。

(a) 位移

(b) 接觸力圖12 兩種模型對比Fig.12 Comparison between CCF and LCP

例2本算例將給出所提方法在柔性多體系統接觸/碰撞動力學中的應用。基于文獻[19]所提的模型降噪方法以及文獻[24]所提的大變形空間梁的共旋坐標法，將梁的廣義應力修正為短時間內的平均應力

(23)

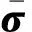
(24)

由于單元應變在共旋坐標系中為小量，因此式(8)可用單元剛度矩陣表示，并按照式(24)修改為

(25)

因此，修正后的節點內力為

(26)

式中：Ke為單元剛度矩陣；ue為單元局部參數，描述截面在單元坐標系下的位移和轉動。

對于圖13所示的柔性雙擺機構，材料密度設為ρ=7 850 kg/m3，彈性模量E=2.1×109Pa，兩根擺長均為L=2 m，截面積均為A=3×10-4m2。機構在重力加速度g=9.81 m/s2作用下，從水平靜止位置落下并于剛性基礎產生碰撞，假定平面光滑無摩擦。

圖13 自由下落并與基礎碰撞的柔性雙擺機構Fig.13 Free-falling flexible double pendulum mechanismimpact with foundation

采用MATLAB ode45常微分方程求解器對該問題進行數值積分，取精度控制參數εr=1.0×10-4和εa=1.0×10-6。得到雙擺結構在不同時刻的構型圖和碰撞力時程，分別如圖14和圖15所示。

圖14 雙擺構型圖Fig.14 Deformed configurations of flexible double pendulum

由圖14和圖15可見，當柔性雙擺的材料剛度較小時(E=2.1×109Pa)，第二根擺在碰撞后變形很大。由于材料較柔，碰撞后桿端并沒有彈離地面，而是進入平順接觸狀態，沿平面滑動一段距離后脫離地面。

圖15 接觸力時程曲線Fig.15 Time lapse of normal contact force

多柔體系統的剛性以及接觸非線性極大的增加了數值求解的困難，數值解的高頻振蕩也往往導致接觸力求解失真。剛性積分器的算法阻尼往往不能有效地衰減高頻振蕩，往往通過在模型中引入少許線性阻尼或結構阻尼的方式進一步濾除高頻振蕩。采用文獻[19]所提的模型降噪方法時可采用常規的積分器(如ode45)進行求解。此外，為了避免磨平碰撞效應，在濾除過高頻率彈性振蕩的前提下，模型中的降噪因子應盡可能的小，以提高數值解的精度。

4 結 論

為刻畫柔體間動態接觸力，選取當前時刻為起點的短時區間[t,t+h]內對縫隙函數進行均勻化，建立了均勻化縫隙函數與接觸力之間的線性互補關系，該方法可綜合考慮碰撞和平順接觸，不必在接觸狀態發生改變時切換模型，同時保證了接觸力的非負性。為了降低高頻成分對求解接觸力的干擾，引入模型降噪方法濾除了過高頻率的高頻振蕩成分，提高了數值求解的穩定性。

數值算例表明，所得結果在定性和定量兩個方面都是合理的。該方法不僅適用于單點接觸，同時也適用于柔體間的多點摩擦接觸問題。將所提均勻化線性互補模型與模型降噪方法相結合，可成為求解大型復雜柔性多體系統接觸碰撞問題的新途徑。