永磁直線同步電機空載反電動勢和推力的解析計算

王明杰 賈宛英 張志艷 徐 偉 司紀凱

（1. 鄭州輕工業大學電氣信息工程學院 鄭州 450002 2. 華中科技大學電氣與電子工程學院 武漢 430074 3. 鄭州大學電氣工程學院 鄭州 450001）

0 引言

永磁直線同步電機（Permanent Magnet Linear Synchronous Motor, PMLSM）結合了永磁同步電機和直線電機的結構特點，具有推力密度大、定位精度高、可靠性好等優點，在電磁彈射系統、無繩電梯直驅系統、數控機床系統、軌道交通直線牽引系統等直線運動領域應用優勢明顯[1-4]。因此，近年來PMLSM 已成為國內外學者和科研機構的研究熱點，其理論及實踐研究越來越系統化，但是仍有一些基礎研究需要進一步完善。

計及齒槽效應的影響，為了獲得準確的電機參數，方便后期對電機進行優化設計，PMLSM中常采用解析法和有限元法分析電機的反電動勢和推力。相對于有限元法，解析法物理概念直觀、計算速度快。有限元法能夠精確求解復雜電機結構的磁場，通用性好，但是前處理建模、后處理求解耗時長，未能直觀地反映設計參數對電機性能的影響規律，在電機結構參數化計算中效率不高，常用來驗證以上模型的正確性。解析法主要包括：二維氣隙相對磁導函數模型[5-7]、保角變換模型[8-11]、精確子域模型[12-16]、等效磁網絡模型[17-20]。文獻[6]采用二維氣隙相對磁導函數模型結合磁路法給出了PMLSM的反電動勢和推力解析式，直觀地反映了結構參數對推力的影響，由于二維氣隙相對磁導函數模型的局限性，未能考慮切向上齒槽效應對電磁參數的影響。計及切向上齒槽效應對氣隙磁場，文獻[9]采用保角變換法分析PMLSM磁場，準確度較高，但需經過多次平面變換，計算較復雜。為了得到更加精確的電機磁場，文獻[13]采用精確子域模型得到了電機的空載磁場和推力，計算結果基本上與有限元結果一致，但邊界條件處理繁瑣，需確定的各次諧波系數較多，公式繁多不直觀，計算量較大。文獻[19]提出新的網格生成方法建立PMLSM等效磁網絡模型，很好地解決了磁路飽和、漏磁對PMLSM電磁參數的影響，但該方法類似于有限元網格剖分，建模工作量隨著節點的增多而增加，導致計算效率不高。

上述解析模型中，二維氣隙相對磁導函數模型與其他模型相比的顯著優點是能以精簡的解析式反映氣隙相對磁導分布，從而能簡便地確定氣隙磁場。目前多數文獻采用二維氣隙相對磁導函數結合磁路法對PMLSM磁場進行計算，僅考慮了二維氣隙相對磁導法向分量，尚未考慮其切向分量。

在保證準確度的前提下，考慮齒槽效應對電機電磁參數的影響，本文提出一種基于改進的二維氣隙相對磁導函數求解電機參數，同時結合分離變量法，用于準確計算定子開槽時電機的氣隙磁場、空載反電動勢和推力。首先建立無槽PMLSM解析模型，給出改進的二維氣隙相對磁導函數解決切向氣隙相對磁導分布，以此建立其與氣隙磁通密度的關系；其次結合改進的二維氣隙相對磁導函數得到電機開槽時的氣隙磁通密度法向和切向分布；最后計算出不同極槽配合下電機的磁鏈、空載反電動勢和推力，并用有限元法驗證解析法的準確性。

1 無槽PMLSM磁場解析模型

為簡化分析，忽略端部效應，永磁體在各方向上磁導率相同且等于空氣磁導率；定、動子鐵心的磁導率為無窮大，磁路不飽和；忽略臨近齒槽效應，定子槽為無限深。基于以上假設，以磁極軸線為原點，建立無槽PMLSM磁場分層模型，如圖1所示，分為1、2、3、4四個求解區域，分別對應定子軛、永磁體、氣隙、動子軛區域。

圖1 無槽PMLSM磁場解析模型Fig.1 Layered model of slotless LPMVM

永磁體磁化方向沿y方向，其磁化強度矢量為M=Myy，對其展開傅里葉級數形式，則

式中，M0為永磁體磁化強度；Br為永磁體剩磁；μ0為空氣磁導率；αp永磁體極弧系數；Lm為永磁體長度，τ為極距。

以矢量磁位Az(x,y)為求解變量，永磁體區域為泊松方程，氣隙區域為拉普拉斯方程，即

式中，Az2(x,y)、Az3(x,y)分別為永磁體區域、氣隙區域的矢量磁位。

通過分離變量法知永磁體區域和氣隙區域的矢量磁位通解為

在各區域磁場邊界條件滿足

式中，hm為永磁體高度；δ為氣隙長度。

根據式（4）～式（6），推出永磁體區域無槽磁通密度解析式為

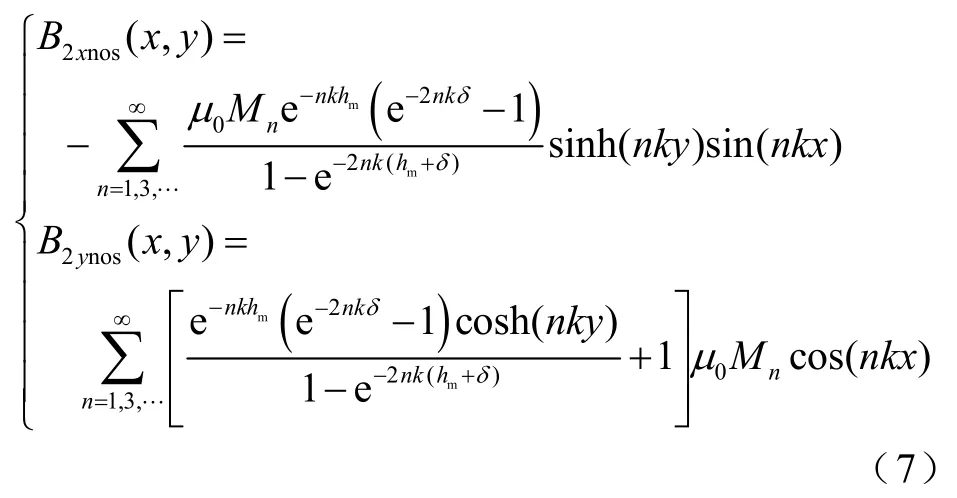
氣隙區域無槽磁通密度解析式為

2 改進的二維氣隙相對磁導函數及有槽氣隙磁場解析

以一槽為分析模型，選取槽中心為原點，采用許-克變換法，PMLSM的二維氣隙相對磁導函數表達式為[5]

式中，a0為槽中心線與A相繞組軸線的距離；ts為齒距；bs為槽寬；β(y)為非線性函數[5]，與槽寬、定動子間距離、氣隙處位置有關，用來確定氣隙相對磁導各次諧波大小。

式（9）中含有常數項和余弦級數項，可知法向氣隙相對磁導分布為偶函數，關于槽中心線對稱。式（9）僅能考慮齒槽效應在法向上對氣隙相對磁導分布的影響，而對于切向上的影響目前未見文獻給出詳細的解析式。根據文獻[8]分析可知，切向氣隙相對磁導分布為奇函數，因此切向上的氣隙相對磁導無常數項，且與法向上的諧波幅值具有相似性，可得切向氣隙相對磁導表達式近似為

式（9）和式（10）構成了改進的二維氣隙相對磁導函數。為了得到考慮齒槽效應時的氣隙磁通密度，將改進的二維氣隙相對磁導函數λr(x,y)寫成復數形式，即

式中，λy(x,y)、λx(x,y)分別為改進的二維氣隙相對磁導函數的實部和虛部。若僅考慮實部，則為改進前的模型。根據式（11）可以得到氣隙不同位置處的二維氣隙相對磁導分布。

有槽氣隙磁通密度等于無槽氣隙磁通密度與改進的二維氣隙相對磁導函數的共軛復數之積[8]，即

式中，Bs(x,y)為有槽磁通密度；Bnos(x,y)為無槽磁通密度。

有槽磁通密度和無槽磁通密度寫成復數形式為

式中，實部表示法向磁通密度；虛部表示切向磁通密度。

由式（11）～式（14）得有槽氣隙磁通密度的法向和切向分量分別為

采用有限元驗證改進的二維氣隙相對磁導分布時 ， 一 般 情 況 下Bxnos(x,y)、Bxnos(x,y)·λx(x,y)、Bxnos(x,y)·λy(x,y)比較小，因此有限元法計算二維氣隙相對磁導公式可化簡為

根據式（8）、式（15）、式（16），得到有槽時氣隙區域的空載磁通密度為

3 空載反電動勢和推力計算

為了得到線圈產生的磁鏈，將式（8）寫成

單匝線圈產生的磁鏈cψ為

式中，La為鐵心長度；ay為線圈節距，ay=y1ts，y1為線圈跨過的槽數。

單匝線圈感應的空載反電動勢為

將式（21）代入式（19）得到氣隙磁通密度B3ys(x,y)為

式中，v1為電機動子速度。

將式（24）代入式（22）得單匝線圈產生的磁鏈cψ為

則一相繞組產生的空載反電動勢為

式中，N1為每相繞組串聯匝數；對于A相θ0=0°，B相θ0=2π/3，C 相θ0=4π/3；kdn為 分 布 系 數 ；為槽開口系數；λ(x,y)、λ(x,y)yx的坐標原點為槽中心線，當y1為奇數槽，則a0=ts/2，cos(mza0)=cos(mπ)；當y1為偶數槽，則a0=0，cos(mza0)=1。

由空載反電動勢的公式知，其大小與無槽氣隙磁通密度的諧波幅值和二維氣隙相對磁導的諧波幅值有關。一般情況下對于整數槽，切向磁通密度較小，可忽略Bxn(n)λm(m)，進一步簡化為只考慮法向磁通密度諧波幅值Byn(n)，方便計算。對于分數槽，尤其是極數多于齒數的極槽配合，切向磁通密度較大，Bxn(n)λm(m)不可忽略。

電機推力為

式中，pe為電磁功率；ia、ib、ic為定子三相電流；I為電流有效值；w1為電源角頻率。

從以上分析可以看出，與其他解析法相比，空載反電動勢和推力的最終解析式均為級數求和計算，避免了積分和微分計算，計算工作量小，提高了求解效率。

4 有限元驗證

為了驗證解析模型的正確性，分別對整數槽和分數槽兩種結構進行分析，PMLSM結構參數見表1，其中每種電機采用兩種槽型結構，分別是槽口寬較小的半閉口槽結構（bs≤ts/2）和槽口寬較大（bs≥ts/2）的矩形槽結構來說明槽口寬對電機參數的影響。圖 2給出了12s14p PMLSM半閉口槽和矩形槽兩種槽型的結構模型。

表1 PMLSM結構參數Tab.1 The structure parameters of PMLSM

圖2 PMLSM結構模型Fig.2 Structural model of PMLSM

4.1 改進的二維氣隙相對磁導和有槽氣隙磁通密度計算

根據式（9）和式（10）得到18s6p、12s14p采用半閉口槽結構和矩形槽結構，在氣隙中心y0=hm+δ/2時改進的二維氣隙相對磁導分布如圖 3、圖4所示。有限元計算改進的二維氣隙相對磁導方法為：以槽為中心在繞組中通入對稱的直流電，使其產生的磁場關于槽中心對稱，得到有槽磁通密度，然后將電機等效為無槽電機，計算同樣的大小直流電流分布在槽口表面的無槽電機氣隙磁通密度，根據式（17）和式（18）得到改進的二維氣隙相對磁導分布。可以看到，解析法和有限元法結果擬合較好，改進的二維氣隙相對磁導法向分量關于槽中心呈偶對稱，切向分量關于槽中心呈奇對稱。同時可以看到，隨著槽寬的增加，切向磁導的誤差稍微增大，這是因為氣隙磁導模型為單槽模型，沒有考慮臨近齒槽效應的影響。

圖3 改進的二維氣隙相對磁導分布（18s6p）Fig.3 The distribution of improved 2D relative permeance about 18s6p PMLSM

圖4 改進的二維氣隙相對磁導分布（12s14p）Fig.4 The distribution of improved 2D relative permeance about 12s14p PMLSM

以18s6p為例，保持氣隙δ=5mm不變，改變槽寬，用解析法得到氣隙中心y0=hm+δ/2處改進的二維氣隙相對磁導變化曲線如圖5a所示。同理保持槽寬bs=3mm和永磁體高hm=7mm不變，氣隙δ取不同長度時，定、動子之間的距離隨氣隙的增大而增大，得到如圖5b所示曲線。由圖5可知，當槽寬與齒距之比增大時，二維氣隙相對磁導法向和切向幅值變化越大，在齒邊角處變化最大。當氣隙長度增大時，二維氣隙相對磁導幅值的變化減小，曲線趨勢逐漸越緩。

圖5 改進的二維氣隙相對磁導與槽寬和氣隙的關系Fig.5 The improved 2D relative permeance versus slot width and airgap

18s6p、12s14p不同槽寬下的氣隙磁通密度分布如圖6和圖7所示，可知改進的二維氣隙相對磁導較好地反映了齒槽效應對磁場法向和切向分布的影響，解決了目前切向磁場上求解困難的問題。

圖6 18s6p氣隙磁通密度分布Fig.6 Flux density distribution of 18s6p PMLSM

圖7 12s14p氣隙磁通密度分布Fig.7 Flux density distribution of 12s14p PMLSM

4.2 空載反電動勢和推力計算：

18s6p、12s14p運行頻率分別為f=4Hz、f=10Hz，由式（26）得到的空載反電動勢結果如圖 8和圖9所示。兩種電機電流有效值均為5A，由式（27）得到的推力計算曲線如圖10和圖11所示。其中圖11給出了12s14p每相繞組串聯匝數相同，分別采用單雙層繞組時的推力對比曲線。表2和表3分別給出了 18s6p 和 12s14p在不同結構參數下的空載反電動勢有效值、推力平均值的數值對比，表中的相對誤差以各電機有限元結果為基準值。

圖8 18s6p空載反電動勢波形Fig.8 No-load EMF of 18s6p PMLSM

圖9 12s14p空載反電動勢波形Fig.9 No-load EMF of 12s14p PMLSM

圖10 18s6p推力波形Fig.10 Thrust of 18s6p PMLSM

由圖 8～圖 11可知，利用解析法、有限元法得到的反電動勢和推力結果基本一致，解析法較好地反映了空載反電動勢、推力隨時間的變化曲線。由表2和表3可以看到，整數槽、分數槽繞組半閉口槽結構結果誤差較小，分數槽繞組矩形槽結構結果誤差稍大。對于矩形槽結構，存在誤差的原因為隨著槽口寬與齒距之比的增大，臨近齒槽效應的影響越來越大，由于氣隙磁導為單槽模型，忽略了臨近齒槽效應的影響，切向磁場誤差變大，在反電動勢和推力上會存在誤差。

表2 18s6p PMLSM空載反電動勢和推力數值對比Tab.2 Comparison of no-load EMF and thrust of 18s6p PMLSM

圖11 12s14p推力波形Fig.11 Thrust of 12s14p PMLSM

表3 12s14p PMLSM空載反電動勢和推力數值對比Tab.3 Comparison of no-load EMF and thrust of 12s14p PMLSM

與其他解析法相比，在保證準確度的情況下簡化了復雜的計算，方便了電機的參數計算分析。由圖 8、圖9可知電機為分數槽時的反電動勢正弦性比整數槽時好。由圖10、圖11及表2和表3可以看出隨著槽寬增大，根據卡氏系數知等效氣隙增大，平均推力略有減小，電機為整數槽時矩形槽結構比半閉口槽推力波動大。由圖11可知，由于分數槽單層繞組的基波繞組系數大于分數槽雙層繞組，且分數槽單層繞組含有較大的電樞反應磁動勢諧波，因此其平均推力、推力波動均大于分數槽雙層繞組。

在求解時間對比上，以分數槽結構 PMLSM 12s14p為例，求解時長為一個電周期，采樣點100個。解析法可一次性求解出二維氣隙相對磁導、氣隙磁通密度、空載反電動勢、推力參數，當諧波最大次數取M=N= 5 0時，計算結果已基本不變。有限元法后處理功能強大，但求空載反電動勢、推力參數需單獨建模，增加了建模時間，改變電機結構如不采用參數化模型同樣增加前處理時間。有限元建模氣隙處單元格剖分長度為0.5mm，模型總剖分節點 29 253個。計算機配置 CPU為 i7-7700HQ，2.8GHz，內存32G，解析法和有限元法仿真耗時分別為2.5s和100s。解析法中所有計算均為求和計算，能快速求出以上電磁參數，求解效率遠高于有限元法，而有限元法求解精度高，計算時間隨剖分網格的增加而增加。

5 結論

本文采用一種改進的二維氣隙相對磁導函數結合分離變量法求解PMLSM電機參數，準確計算了不同電機結構下的改進的二維氣隙相對磁導、氣隙磁通密度、空載反電動勢和推力，并用有限元法驗證了解析結果的正確性。與其他方法相比，提出的方法準確度較高，降低了磁場求解過程的復雜性，是目前解析法中分析簡便、工作量小、計算效率高、通用性好的一種，且適用于整數槽和分數槽結構PMLSM性能的分析，有益于 PMLSM的電磁分析和優化設計。