基于高斯似然估計因子分析的點云配準算法
李 燦 孫 未 張力云
(成都理工大學核技術與自動化工程學院 四川 成都 610059)
0 引 言
點云配準技術是一種重要的數字檢測技術,現已蓬勃發展并廣泛運用于各個行業,如計算機視覺、高精度加工、無損檢測、虛擬現實等[1-4]。通過三維掃描儀對物體表面進行多角度掃描,得到不同視角下的三維點云數據,再將所得的點云數據進行配準,即可得到完整的模型。Besl等[5]提出的最近點迭代(Iterative Closest Point,ICP)算法廣泛運用于點云配準中,作為經典的配準算法,其主要手段是通過尋找兩個點集的對應點,并計算其變換矩陣,但該算法容易陷入局部最小值并且效率不高[6-7]。
由于ICP算法存在的部分缺陷,眾多學者都提出了各種各樣的改進算法來減小配準誤差和提高配準效率。Bae[8]提出基于曲率和法向變化率的幾何基本最近點迭代(GP-ICP)算法,該算法使得ICP算法對迭代初始值的要求降低。Ying等[9]提出基于七維空間迭代的Scale-ICP算法,雖然其收斂速度較快,但對迭代過程非常依賴且僅能應用于點云整體存在相似變換的情況。Sharp等[10]提出的最近點迭代(ICPIF)算法主要利用不變特征配準,該算法可實現局部重疊的點云配準,但是在理論上對點云數據缺失情況下的配準很難實現。
本文提出一種基于高斯似然估計因子分析的點云配準算法。將點云配準的數學公式模型擴展為因子分析模型,這樣便將點云配準轉化為對因子模型參數的求解;采用多元高斯函數對點云數據進行逼近,并通過EM算法求解出因子載荷矩陣,再利用所求得的因子載荷矩陣完成對點云的配準。實驗表明,與其他幾種算法相比,即使在點云無序、數據存在遮擋、缺失不完整,以及噪聲環境下,本文算法仍可實現快速精確配準,收斂速度快,具有良好的魯棒性。
1 基本原理
1.1 因子分析
一組D維的觀測數據X={x1,x2,…,xN}的正交因子模型為:
(1)
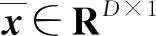
(2)
通過上述正交因子數學模型可知,觀測數據X的協方差矩陣為:
∑=AAT+φ
(3)
式中:φ為特殊因子矩陣ε的協方差。
1.2 點云配準原理
將源點云P={p1,p2,…,pn}和目標點云Q={q1,q2,…,qm}進行剛性幾何變換:
pi=Rqj+ti=1,2,…,n;j=1,2,…,m
(4)
式中:R∈R3×3為旋轉矩陣,且RTR=I;t∈R3×1為平移向量。由式(3)可知,兩點云的協方差矩陣可表示為:
由式(4)可得到兩點云協方差矩陣的關系為:
∑P=R∑QRT
(5)
點云數據在實際運用中可能會有噪聲干擾,可以通過正交因子模型對數據處理,計算出兩點云的因子載荷矩陣,可以將特殊因子協方差矩陣看作是噪聲項。所以降噪后的點云協方差矩陣為:
(6)
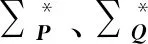
ΛP=ΛQ
(7)
綜上所述,可得:
(8)
為了計算出平移向量t需要先計算出點云P和點云Q的均值點,即:
(9)
進一步得到:
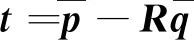
(10)
2 參數求解
2.1 極大似然估計
對樣本X={x1,x2,…,xN}進行極大似然估計:

(11)
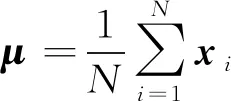
2.2 EM迭代
為了求解2.1節的最大值,這里采用最大期望算法(Expectation Maximization Algorithm,EM)對上述問題進行求解,EM算法分為兩個部分。E步:計算完整數據的對數似然函數的期望;M步:通過將中間量最大化的值來獲得新的參數值。
由2.1節可知為了估算旋轉矩陣,需要求解的參數為AP、AQ、φP、φQ,在EM算法下需要計算每個觀測值的概率屬性γi,同樣為了計算γi需要假設一個中間隱藏變量fi,計算結束之后可消掉。則代價函數為:
(12)
式中:θ={μ,A,φ}表示待求解參數;fi是第i個中間隱藏變量且f~N(O,I);γi(fi)是第i個中間隱藏變量的觀測值。E步,計算γi(fi),由高斯邊緣分布條件可得X和z的聯合分布為:
(13)
因此,有:
(14)
根據多元高斯分布公式,得到:
(15)
M步,將代價函數進一步表示為:
(16)
對A求偏導:
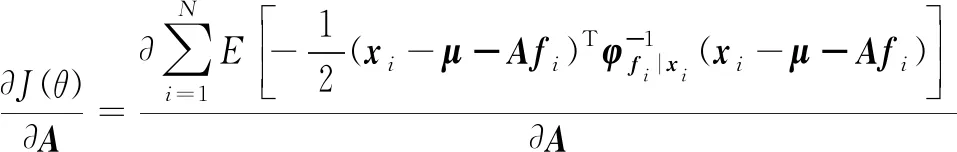
(17)
令式(17)等于0,可得:
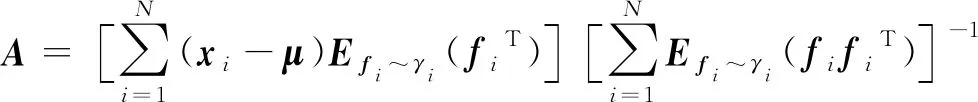
(18)
由式(13)可知:
(19)
綜上所述:
(20)
求解過程中μ值不變。同理,用此方法對φ求偏導,省略推導過程,得到推導結果:
A(μfi|xi(μfi|xi)T+∑fi|xi)AT]
(21)
本文算法流程如圖1所示。
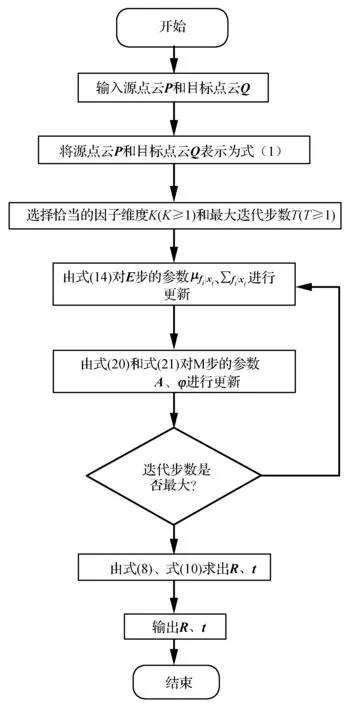
圖1 本文算法流程
本文算法是在MATLAB 2017a版本下實現的,具體步驟如下:
Step1通過式(1)將點云P和點云Q表示為正交因子模型。
%E步:
for i=1:N
muf(:,i)=A′/(A*A′+phi)*(X(:,i)-mu);
%更新每一個中間均值變量muf
Ef(:,:,i)=eye(K)-A′/(A*A′+phi)*A;
%更新每一個中間協方差變量Ef
end
Step3由式(20)分別更新點云P和點云Q的正交因子載荷矩陣AP、AQ和殘差矩陣φP、φQ,具體代碼如下:
%M步:
%更新A
A1=zeros(D,K);
%初始化中間變量矩陣為D×K的矩陣
A2=zeros(K,K);
%初始化中間變量矩陣為K×K的矩陣
for i=1:N
A1=A1+(X(:,i)-mu)*muf(:,i)′;
%計算(X(:,i)-mu)*muf(:,i)′的累加和A1
A2=A2+muf(:,i)*muf(:,i)′+Ef(:,:,i);
%計算muf(:,i)*muf(:,i)′+Ef(:,:,i)的累加和A2
end
A=A1/A2;
%利用累加和A1和A2更新因子載荷矩陣A更新phi
P=zeros(D,D);
%中間殘差矩陣初始化為D×D的矩陣
for i=1:N
P=P+X(:,i)*X(:,i)′-X(:,i)*muf(:,i)′*
A′-A*muf(:,i)*X(:,i)′+A*(muf(:,i)*muf(:,i)′+
Ef(:,:,i))*A′;
%采用累加和的方式更新中間殘差矩陣P
end
phi=diag(P/N);%取1/N倍中間殘差矩陣的對角線元素
%得到1×D的向量
phi=diag(phi);%將1×D的向量轉化為對角線殘差矩陣,
%完成對對角線殘差矩陣phi的更新
Step4重復Step2和Step3直至收斂,由式(6)-式(8)利用AP、AQ估算旋轉矩陣R。
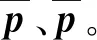
Step6由式(10)估算出平移向量t。
3 實驗與仿真分析
仿真主要是通過對來自斯坦福大學的公開點云數據Bunny(分辨率:31 607個點)和Horse(分辨率:48 485個點)三維點云數據進行仿真配準,和對來自三維激光掃描儀HandySCAN 700分別從正面與側面對現場實際物體進行掃描的實驗數據進行配準,噪聲為高斯白噪聲。三維激光掃描儀HandySCAN 700配置參數如下:
產品用途:行業掃描
掃描元件:CCD
產品類型為3D掃描儀
掃描范圍:自由掃描為0.1~4.0 m
掃描速度:480 000次測量/秒
產品尺寸:122×77×294 mm
產品重量:0.85 kg
使用條件如下:
電源類型:100~220 V
工作溫度:5℃~40℃
工作濕度:10%~90%
使用方式:手持
激光類別:2級
精度:最高0.03 mm
實驗預仿真環境為:MATLAB 2017a版本、i7-6700HQ四核處理器和GTX965M。為了確保配準精度,實驗與仿真是在不能受到有其他軟件的影響的條件下進行的。
3.1 經典配準
通過對Bunny和Horse點云的隨機旋轉和平移得到目標點云,然后對Bunny目標點云做隨機丟失25%處理,對Horse的目標點云添加50 dB的高斯白噪聲。點云初始狀態如圖2所示。

圖2 Bunny和Horse點云的初始狀態
分別利用本文算法、CPD算法、Go-ICP算法對三維點云數據配準,比較三種算法的配準精度和時間,配準效果如圖3所示。


圖3 三種算法對Bunny和Horse點云的配準效果
三種算法配準精度和配準時間如表1所示。

表1 三種算法的配準時間和配準誤差
由圖3和表1可知,CPD算法對Bunny和Horse點云配準在時間上明顯多于本文算法和Go-ICP算法。在配準精度方面,本文算法對Bunny的配準誤差要略大于Go-ICP算法,但對Horse的配準精度更優于其他兩種算法。
3.2 實物配準
為證明本文算法具有實用性,采用三維激光掃描儀HandySCAN 700分別從正面與側面對兩組物體進行掃描,從正面與側面分別掃描的目的是為了得到不同視覺下的點云數據集。得到Bottle和Banana點云的初始狀態,如圖4所示。其中:Bottle源點云(右)分辨率為21 450個點,目標點云(左)分辨率為21 430 個點;Banana源點云(左)分辨率為45 271個點,目標點云(右)分辨率為46 370 個點。

(a) Bottle (b) Banana
將本文算法與CPD算法和Go-ICP算法的配準效果進行對比,結果如圖5所示。
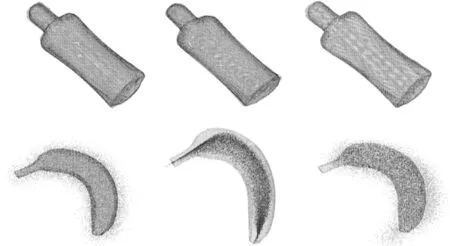
(a) (b) (c)
三種算法對Bottle和Banana點云的配準時間和配準誤差如表2所示。

表2 三種算法對Bottle和Banana點云的配準誤差和時間
實驗結果表明,對Bottle和Banana進行點云配準時,本文算法所需的時間明顯少于CPD和Go-ICP兩種算法。三種算法在對Bottle進行點云配準時的配準誤差相差甚微,但本文算法對Banana配準時的誤差要明顯小于其他兩種算法的精度。
3.3 現場掃描機械點云配準
為充分驗證本文算法對實物掃描數據進行配準的有效性,用便攜式激光掃描儀 (HandySCAN 700TM) 對現場機械器件從正面與側面分別進行掃描,從正面與側面分別掃描的目的是為了得到不同視覺下的機械點云數據集,進行實物數據采集,然后對掃描數據做相應處理后,再進行配準。機械器件目標點云(右)分辨率28 437個點,和待配準點云(左)分辨率21 328個點,初始狀態如圖6所示。

圖6 機械器件的初始狀態
將本文算法與CPD算法和Go-ICP算法分別配準,配準效果如圖7所示。
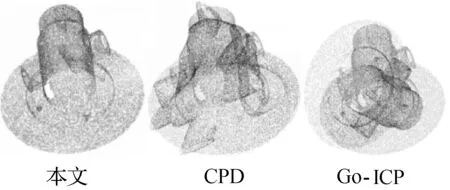
圖7 配準效果圖
三種算法的配準時間和精度如表3所示。
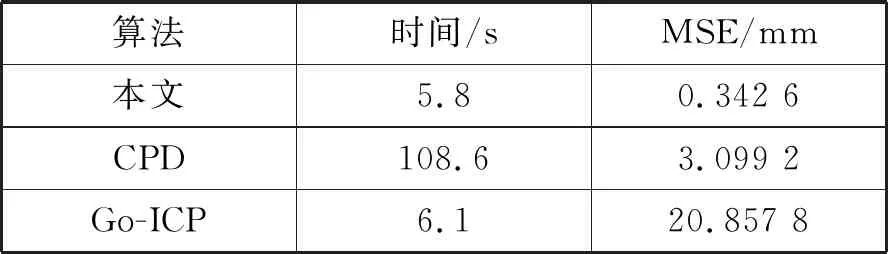
表3 三種算法的配準時間和配準誤差
由圖6和表3可知,對機械器件進行點云配準時,本文算法在配準時間上與Go-ICP算法相差甚微且遠優于CPD算法,但在配準精度方面,本文算法明顯優于其他兩種算法。
綜合分析發現,本文算法具有較好的實用性。該算法的應用前景主要是在歷史文物保護、工程測量、醫學圖像重建等方面。
4 結 語
本文針對數據存在白噪聲、數據缺失、無序,以及仿射情況下的三維點云提出一種基于主成分因子法的點云配準算法。將帶白噪聲的點云數學模型擴展為正交因子模型,從而將點云配準問題轉化為對模型參數的求解;通過運用極大似然法得到因子載荷矩陣,進一步精確化模型參數,從而實現點云配準。實驗表明,本文算法有效提升了配準精度和效率;與Go-ICP和CPD兩種算法對比,本文算法的穩定性較高。

