基于多目標遺傳算法的柴電混合動力船舶功率分配優化

張 程 賈寶柱，2* 鄒佳奇

1(大連海事大學船舶電氣工程學院 遼寧 大連 116026)

2(廣東海洋大學海運學院 廣東 湛江 524088)

0 引 言

混合推進船舶(Hybrid Propulsion Vessel-HPV)指單船包含兩種或兩種以上的動力形式，如液壓-電力推進方式[1]、風帆助航推進[2]、噴水推進[3]，以及柴-電混合推進[4]等。柴-電混合系統是混合推進系統的主要形式之一，在傳統柴油機直接推進系統的基礎上增加了電力推進方式以提高船舶的操控性能，既能利用操縱性好、噪音低的柴油發電機作為動力源，又可以兼顧柴油推進裝置單機功率高、輸出扭矩大的優勢。混合推進系統控制問題主要研究如何改善多種工作模式下功率配置方案，在滿足動力需求的前提下實現降低燃油成本、減少排放、提高船舶經濟性的目的。

混合動力船舶與混合動力汽車在動力形式上非常類似，本質都是通過利用多種動力源(柴油機、汽油機、蓄電池等)驅動船舶或汽車的工作運行。目前，國內外專家學者對于混合動力汽車的相關研究已經頗有成果，這對于研究混合動力船舶有一定的借鑒意義[5-10]。在船舶相關的研究中，Zahedi等[11]考慮了船舶在多種工況下的電力負載變化，提出了一種最小化燃油消耗率的控制策略，根據船舶航行平均需求功率和功率變化特性去制定發電機組的工作準則，使其工作在最優工作狀態，優化后的帶有儲能裝置的直流電力系統與交流系統相比，顯著地降低了燃油消耗。Mahdi等[12]采用帶有約束條件的粒子群優化算法，設計了由原動機、發電機組等動力源的最優輸出功率組合。

本文以深水三用工作船(Deep Water Anchor Handling Tug Supply Vessel, DW-AHT)混合動力系統為主要對象，研究其在不同工況模式下的動力系統最優分配方案，以滿足動力系統節能及低排放的多重指標要求。不同于一般的客船或貨船的性能需求，深水三用工作船要兼顧航行、定位和拖帶等工況模式。本文以節能和排放作為目標參數，采用多目標遺傳算法NSGA-II與混合整數規劃相結合的方法，合并所有的Pareto最優解，得到合并的Pareto前沿。之后利用模糊決策方法，為每種工作模式選出最優動力分配方案。本文試圖得到可用于優化實際船舶動力分配的相關理論依據，進而達到提高船舶經濟性、降低環境影響的目標。

1 混合動力推進系統模型

深水三用工作船推進系統由兩臺獨立操作的主柴油機直接驅動的舵槳推進系統、兩臺電力驅動的全回轉推進器和三臺側推構成，如圖1所示。動力系統包括兩臺主機SG1、SG2和4臺柴油發電機組DG1-DG4，通過各自的主開關為高壓母排Bus1和Bus2供電，兩臺全回轉推進器M6、M7分別連接至Bus1和Bus2，為實現分區供電，兩端母排之間由區聯開關隔開。M4、M5兩臺艏側推和M3艉側推可為船舶提供側向推力，主柴油機主要用于驅動#1和 #2主推進器，還可以帶動軸帶發電機SG1、SG2為母排供電。推進電機M1和M2通過#1和 #2主齒輪箱驅動相應的主推進器。各推進器的位置通過以船舶型心為原點，右舷方向為Y軸正向的坐標值表示，具體如圖2所示。

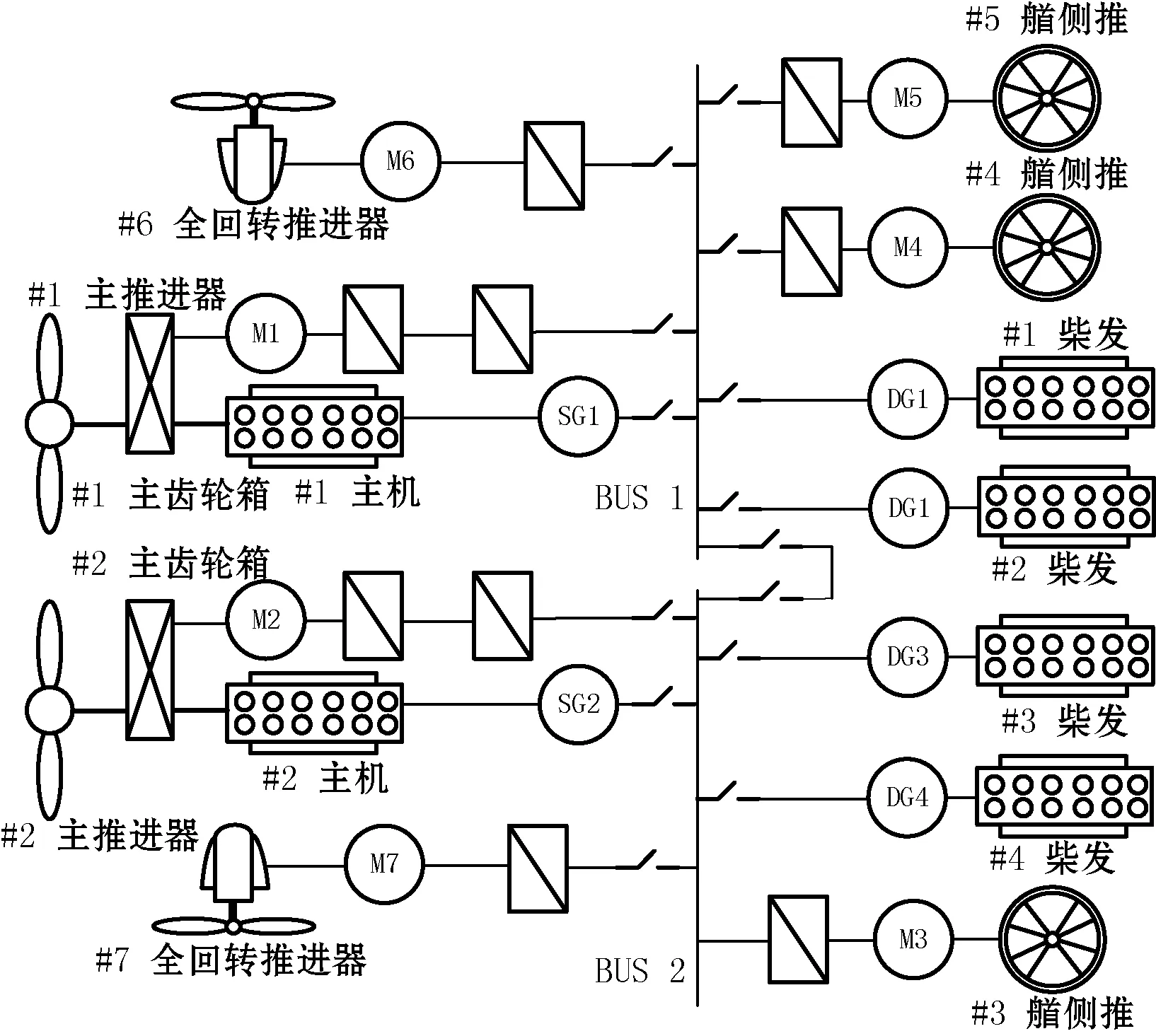
圖1 深水三用工作船動力系統結構圖

圖2 推進器布置圖

動力系統可以分別工作在PTO(Power Take Off)模式、PTH(Power Take me Home)模式和BOOST模式下，對應船舶的不同推進工況要求，如表1所示。PTO模式即為軸帶發電機模式，此模式下由主柴油機驅動主推進器做功，同時剩余功率驅動軸帶發電機SG1、SG2發電為船舶電網供電。PTH模式和BOOST模式通常被稱為PTI(Power Take In)模式。PTH模式適用于低航速航行工況，此時船舶所需推進力較小，主柴油機不工作，軸帶電機此時作為電動機，驅動主推進器。BOOST模式也稱為助力模式，當主柴油機直接驅動螺旋槳所產生的推力不能滿足要求時，推進電機在柴油發電機提供的電能驅動下，通過齒輪箱可以進一步提高主推進器的推進功率。

表1 動力系統工作模式

2 目標函數

2.1 混合推進系統燃油消耗成本

對在正常工作狀態下的船舶來說，混合推進系統的燃油消耗成本包括主機油耗成本和發電機組油耗成本。主機和發電機組的原動機都屬于柴油機，柴油機的每小時燃油消耗量曲線可近似用一個關于負荷的二次多項式函數來表示：

(1)

式中：g(Pi)為第i臺柴油機每小時的燃油消耗量，單位為g/h；ai、bi和ci為第i臺柴油機的多項式系數；Pi是第臺柴油機的負荷功率，單位為kW。

燃油消耗率是指柴油機每小時、每單位功率的燃油消耗，表示為：

(2)

根據相關技術手冊，主機一般使用重油，發電機組使用輕柴油，考慮兩種燃料的價格不同，柴油機的油耗成本可以表示為：

(3)

混合推進系統燃油消耗總成本可表示為：

(4)

式中：F(Pi)為混合推進系統燃油消耗成本，單位為美元/h；N為柴油機臺數；si為第i臺柴油機的運行狀態，運行時si=1，否則為0；Costi為第i臺柴油機消耗的燃油價格，單位為美元/t。

2.2 污染氣體排放量

船舶在海上航行時，需要控制污染氣體的排放，以減小空氣和海水污染。本文選取船舶排放氣體中的氮氧化物NOx為目標。柴油機的每小時NOx排放量曲線可近似用一個關于負荷的二次多項式函數來表示：

(5)

式中:e(Pi)為第i臺柴油機每小時的排放量，單位為g/h；αi、βi和γi為第i臺柴油機的排放多項式系數。則船舶每小時NOx排放總量E(Pi)(單位為t/h)可表示為：

(6)

3 約束條件

3.1 柴油機發力約束

在正常工作條件下，對不同的柴油機應該設置不同的運行功率限制，以防止超負荷或運行在過低負荷，對其造成損傷。

(7)

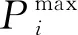
3.2 船舶功率平衡約束

若不考慮系統的功率損耗，船舶混合動力系統發出的功率應該與船舶所需功率相平衡。船舶所需功率Ptotal包括用于推進的功率Pprop和供給用電負載的功率Pelec兩部分，表示為:

(8)

3.3 推進電機功率約束

發電機組輸出的功率包括用于推進的功率和用于發電的功率。發電機組用于推進的功率應不超過推進電機能輸出的最大輸出功率。另外在極限情況下，假設用于發電的功率全部由發電機組承擔，則有：

(9)

4 多目標遺傳算法及模糊決策

遺傳算法(Genetic Algorithm，GA)是通過借鑒進化生物學中的諸如遺傳、突變、自然選擇、雜交等現象而發展完善的進化算法[13]。遺傳算法能夠在搜索過程中通過上述現象進行進化，自適應地控制搜索過程，并獲得最優解。在之后的發展中，非支配排序遺傳算法(NSGA)在解決多目標的問題上非常有效，一般用來解決多目標優化問題。優化問題的解一般為一組解，為了得到最終符合決策者的解，采用模糊決策進行最終解的決策。

4.1 多目標遺傳算法

在多目標優化中，目標間可能存在相互制約的關系，改善某個目標將會使其他目標惡化，因而問題的解常用帕累托(Pareto)前沿來表示，在Pareto前沿上的解稱為非支配解。要獲得非支配解，首先比較并判斷對種群中的個體的支配關系。任意選取兩個個體p和q，進行以下判斷：若pq，則把p加入到受q支配的集合Sq中，同時p的被支配數增加1。循環進行直到種群內的所有個體都兩兩比較完畢。之后再遍歷一遍種群，判斷其中每個個體的被支配數，若為0，說明該個體不受其他任何個體支配，即為一個非支配解。

根據混合動力船舶動力系統的工作特點，本文采用非支配排序遺傳算法NSGA-II來求解Pareto前沿。NSGA-II是在NSGA的基礎上改進得到的一種多目標進化算法(Multi-objective Evolutionary Algorithm, MOEA)，采用了快速非支配排序和精英策略，可以加快搜索過程中的收斂速度，并對秩相同的個體根據排擠機制選擇保留，有效地保護最優解的多樣性。

完整的非支配排序多目標遺傳算法(NSGA-II)步驟如下：

Step1隨機產生初始化種群P0，種群大小為N，并計算種群內個體的適應度，將進化代數設置為t=0。

Step2對初始種群P0進行非支配排序，每個種群的適應度即為其非支配水平，通過排序，每個個體得到一個RANK值，并計算擁擠距離。

Step3通過競賽法選擇精英個體，并通過交叉、變異操作，生成一個種群大小同樣為N的子代種群Q0，并再次計算適應度作為非支配水平。

Step4將子代種群Ot和父代種群Pt合并，得到一個種群大小為2N的新種群Rt。

Step5對Rt采用擁擠比較算子排序，依次選取排序最優的個體復制到新的種群Pt+1，直到新種群規模為N，此時為一次循環，循環代數t加1。

Step6判斷是否達到最大迭代次數tmax。若不滿足則重復Step3-Step5，直到滿足條件，算法停止。

算法流程圖如圖3所示。

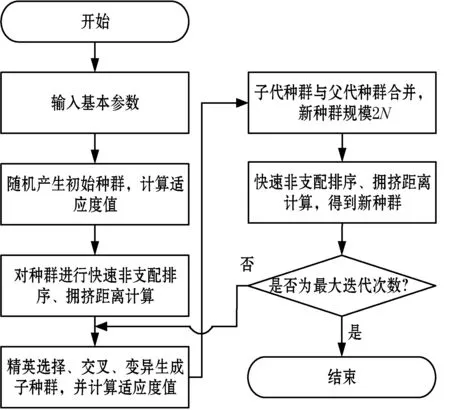
圖3 非支配排序多目標遺傳算法流程

4.2 約束處理

在求解具有約束的優化問題時，會出現能否收斂到全局最優解的問題，沒有約束的優化問題則不會。約束條件的產生會導致在種群進化的過程中產生不滿足約束的一些個體，所以需要對約束進行處理，保證算法的正確性。

由于在NSGA-Ⅱ算法中采用錦標賽選擇算子，存在對種群中的個體兩兩比較的過程，借此過程，可以確定兩個體之間的約束對比情況，采用約束支配的定義處理約束條件[14]。

當以下任意條件成立，稱解p約束支配q。

(1)p為可行解，q為不可行解。

(2)p和q都為不可行解，但p具有更小的約束違反程度。

(3)p和q都為可行解，且p支配q。

約束違反程度函數可定義為：

(10)

式中：約束條件gi(X)和hj(X)滿足條件：gi(X)≥0，hj(X)=0；gi(X)表示當gi(X)≤0時返回0，而當gi(X)>0時返回|gi(X)|。即滿足約束的條件下，約束違反程度等于0；不滿足約束時，約束違反程度大于0。可以得到的結論是，任意可行解的RANK值都比不可行解的RANK值低，而在兩個不可行解中，約束違反程度小的RANK值更低。因此，采用這種約束處理方法使得可行解更容易被選中，而不可行解會在進化過程中被逐漸拋棄，且無須自定義參數。

4.3 模糊決策

模糊性是人類思維和客觀事物普遍存在的屬性之一，而模糊集合論則是處理模糊現象的有效工具。模糊決策正是模糊集合論與決策理論相結合的產物[15]。

運用NSGA-Ⅱ算法可以得到所有滿足約束的船用主機和發電機組需要發出的功率值，即由算法求得的Pareto前沿，為一組解。理論上，這組解全部可以被認為是當前約束條件下的最優解。通過模糊決策的方法，可以從這組最優解中，選取最符合決策者目的的折衷解。對一組Pareto前沿的最優解進行模糊化處理，其隸屬函數表示為:

(11)

式中：μi是模糊化后的目標函數;fi是最優解的第i個解;fi,min是最優解的最小值;fi,max是最優解的最大值。

之后，把燃油消耗成本和污染氣體排放量作為因素集，對在某確定工況下的最優解作因素評價，構成模糊評價矩陣。需要說明的是，因素評價矩陣的設定會受到人為主觀因素的影響，設定的值可以根據決策者的傾向和意圖來改變。為了便于計算和考慮仿真的真實性，對于本文仿真需要的混合動力船舶的四個工作條件，將進行模糊化處理后的隸屬函數進行線性化的因素評價，評價矩陣在表2中給出。

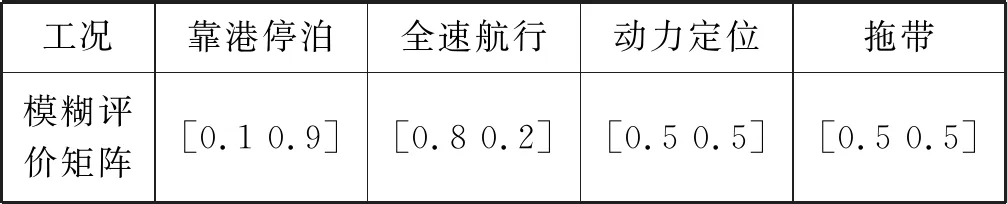
表2 典型工況模糊評價矩陣

5 仿真計算及結論

5.1 仿真參數

DW-AHT有六個柴油發動機，其中有兩個主發動機、三個發電機和一個備用柴油發動機。具體參數見表3。為了保證仿真工作的真實性，在仿真過程中，船舶主發動機和發電機的工作負荷范圍規定在30%～100%之間。在船舶運行過程中，如果兩臺主發動機或兩臺以上的發電機同時運轉，根據船用柴油機的工作特性，應確保其原動機負荷相同。

表3 船舶主機和柴油發電機主要參數

船舶勻速航行中，螺旋槳推力和船舶所受阻力平衡。可以通過計算航行時所受阻力可得到螺旋槳后功率，考慮機槳功率傳遞效率，進而可得到所需推進功率[16]。船舶在航行中所需總功率為推進所需功率和船上其他負載所需功率之和。本文考慮該深水三用工作船在某一次出行任務中分別經歷的拖帶(T)、動力定位(DP)、全速航行(FS)、靠港停泊(HB)四種典型工況下的功率分配問題。四種工況下的所需功率經過計算后如表4所示，為方便計算，每種工況下所需的電力功率假定為定值，且只受工況變化的影響，計算方式根據查閱該船電力負荷表計算得出。

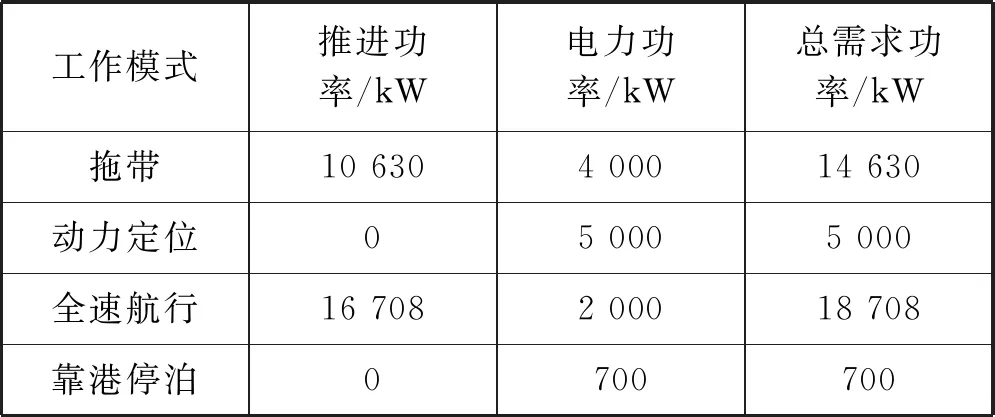
表4 典型工況所需功率

假設船舶在某一天12小時的工作狀態和速度為：靠港停泊(HB)2小時后，以全速(FS)航行4小時，平均速度為18節，到達海上某個地方后，進行動力定位(DP)3小時，最后以100噸的牽引力，在拖曳(T)工況下，以8節的平均速度航行3小時。具體的航速變化如圖4所示。

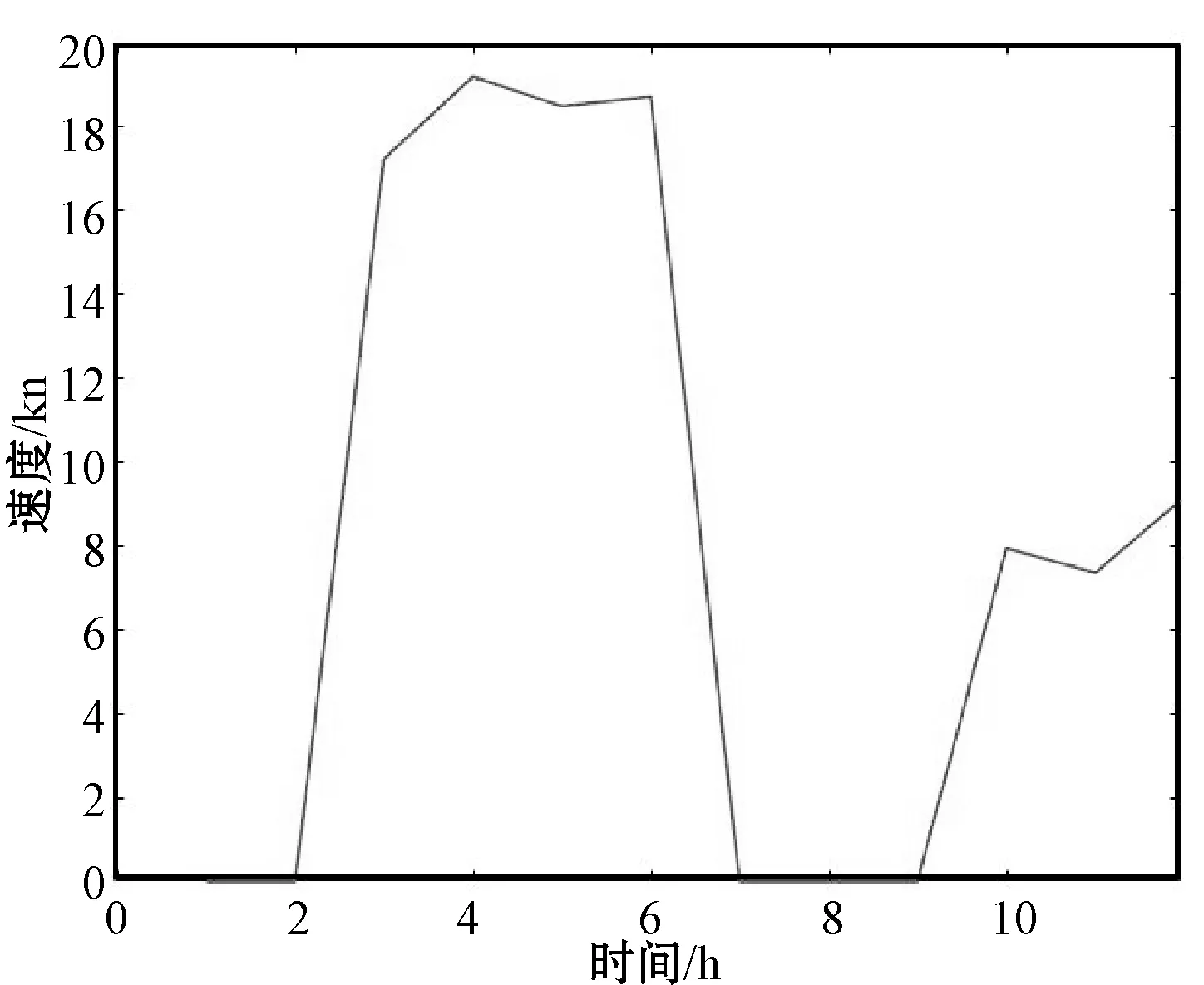
圖4 航速隨時間變化圖

5.2 仿真計算

圖5-圖8分別為使用NSGA-Ⅱ算法針對5.1節中提出的典型工況進行的計算，得到最終的Pareto前沿。在全速航行和拖帶工況下，相對連續和平滑的曲線為所有最優解組成，組成曲線的每一個點都是一個Pareto最優解，代表一個有效方案。靠港停泊和動力定位工況下的Pareto前沿是一個或幾個散點，每個點都代表一種有效的解決方案。通過使用模糊決策算法，可以在這些Pareto前沿中選擇最符合決策者要求的解。最終結果見表5。

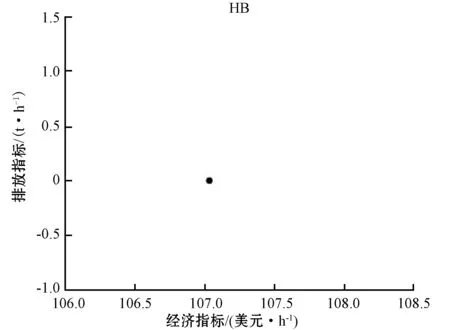
圖5 靠港停泊工況下的Pareto前沿

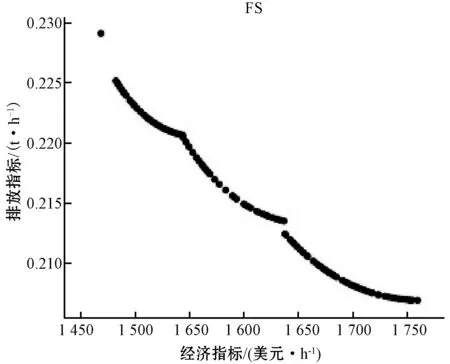
圖6 靠港停泊工況下的Pareto前沿

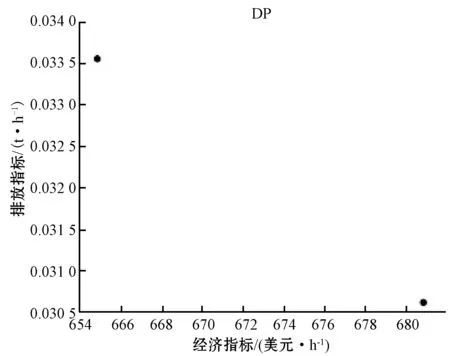
圖7 動力定位工況下的Pareto前沿

圖8 拖帶工況下的Pareto前沿

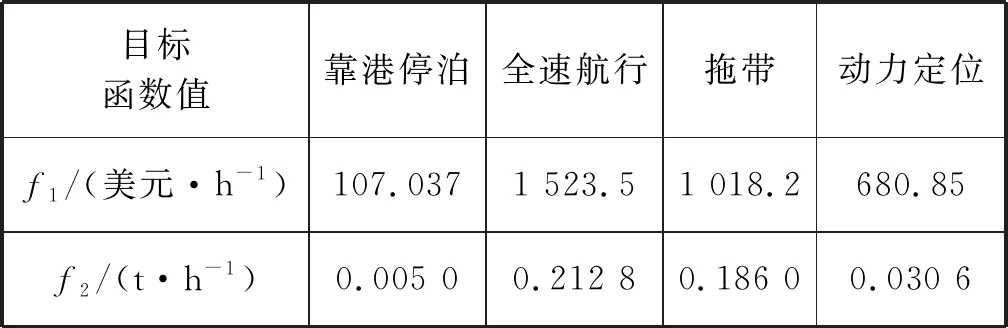
表5 對Pareto前沿模糊決策后的最優解

若在每種工況下進行單目標的優化計算，可以獲得該目標的最佳值。若兩個目標同時作為目標函數，則兩個目標不可能同時達到最小值，而是一個折衷解，這也正是多目標優化算法的作用。表6為只把燃油成本作為目標優化的單目標優化結果，此時的污染氣體排放不再作為目標和約束條件，進行計算所得結果。

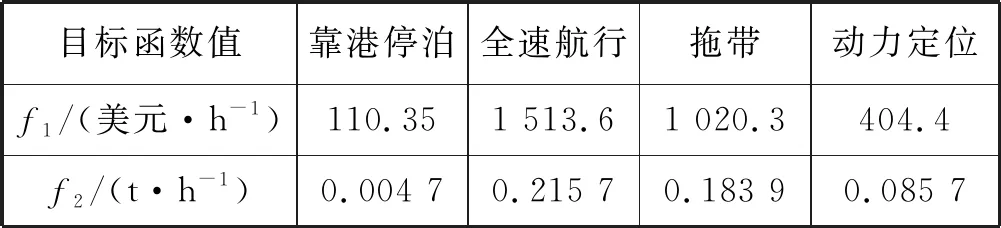
表6 以燃油成本為單目標優化的結果

對兩次結果進行分析，以拖帶工況為例，如果只考慮經濟指標，單目標優化后的最優值為1 020.3美元/h，相應的排放指標為0.183 9 t/h，此時燃料消耗量為低。應用多目標優化算法后，優化得到的經濟指標最優值為1 018.2美元/小時，最優排放指標為0.186 0 t/h。可以看出，燃油消耗和排放指標，不能同時“完美”降低，污染氣體排放目標和燃油成本的目標，基本滿足“一升一降”的趨勢。在動力定位的工況下，若只考慮船舶的整體經濟性，燃料成本可以降低至404.4美元/h，但與經過了多目標優化和模糊決策后的結果相比，污染物的排放增加了接近1.6倍。以上結果表明，將多目標優化模型應用在柴電混合動力船舶功率分配的問題上，能夠在考慮經濟效益的同時減少污染，給出最合適的方案。

6 結 語

本文研究了針對柴電混合動力船舶的功率分配的優化問題。在混合動力船舶中，主柴油機和柴油發電機組都可以為船舶負載提供功率，以此建立柴油機燃油消耗成本和污染物排放為目標的多目標優化問題，根據混合動力船舶工作特點，在約束條件中，引入系統功率平衡和柴油機發力約束，用NSGA-Ⅱ算法解得Perato前沿，再用模糊決策的方法解得最優解。通過MATLAB仿真驗證，得到以下結論：

(1) 針對柴電混合動力船舶所建立模型合理有效，能夠應用于在多目標條件下的求解混合動力船舶功率分配問題。

(2) 運用NSGA-Ⅱ算法和模糊決策相結合的方法能夠較好地解決多目標優化問題，可以兼顧船舶經濟指標和排放指標，在一定程度上提高船舶能效。