改進的TLBO及其在自來水供水量預測中的應用

左智科 李一龍

摘 要：為準確預測城市自來水供水量，提出采用教與學優化算法（TLBO）優化的極限學習機預測方法。針對TLBO算法收斂精度低、易陷入局部最優的不足，提出一種改進的TLBO算法（ITLBO）。在ITLBO中，增加一個最差學生補習階段，通過老師對該學生單獨輔導或者采用一個反向學習策略快速提升學生成績;在此基礎上，采用一種干擾算子對老師進行擾動，增強種群跳出局部最優的動能;最后，將ITLBO算法用于優化調整極限學習機（ELM）模型的輸入權值和隱層閾值參數，并構建ITLBO-ELM自來水供水量預測模型。將ITLBO-ELM模型用于上海市自來水供水量的預測實驗，仿真結果表明該模型能夠準確預測自來水供水量。

關鍵詞：預測;極限學習機;教與學優化算法;反向學習;優化

Abstract：In order to predict the total amount of city tap water supply accurately， a predicting method of the extreme learning machine （ELM） optimized by teaching-learning-based optimization was proposed. An improved TLBO algorithm （ITLBO） was proposed to solve the problem of low convergence accuracy and easy to fall into local optimization. In ITLBO， an extra tutoring stage was added for the worst student， and the teacher could help the student individually or adopt the opposition-based learning strategy to quickly improve the student's performance. On this basis， a disturbance operator was used to perturb the teacher position， which increased the kinetic energy of the population to jump out of the local optimum. Finally， the improved ITLBO algorithm was used to optimize and adjust the input weight and hidden threshold parameters of ELM model， and the ITLBO-ELM water supply prediction model was built. ITLBO-ELM model was used to predict the tap water supply in Shanghai. The simulation results show that the model can accurately predict the tap water supply total amount.

Key words： prediction; extreme learning machine; teaching-learning-based optimization; opposition-based learning; optimization

水資源是人類社會基礎性自然資源。隨著人口規模和經濟社會的持續發展，工業與居民自來水用水量增長，導致城市水資源供需矛盾日益激化。用水預測對于有效管理供水設施以滿足城市日益增長的需求至關重要，準確預測城市需水可為供水環節優化調度提供重要決策依據[1-2]。高級機器學習技術可用于基于特征的預測，在水資源需求分析方面應用廣泛[3-4]。極限學習機（ELM）是一種單隱層前饋神經網絡，是由HUANG Guangbin等[5]根據Moore-Penrose Pseudoinverse廣義逆矩陣提出的學習算法。很多研究者通過優化算法確定模型輸入權重和隱層偏差來提升ELM算法的預測性能[6-8]。

教與學優化算法（TLBO）是一種元啟發式優化方法[9]，具有結構簡單、性能優良等特征，在解決許多科學和工程問題方面表現出卓越的性能[10-11]。為提升ELM算法對城市自來水供水量預測的準確性，筆者采用改進的TLBO算法（ITLBO）對ELM算法中的輸入層權值和隱層閾值進行優化調整，構建ITLBO-ELM預測模型，并以上海市自來水供水量為研究對象，采用自來水供水量歷史數據對模型進行訓練、預測，仿真結果顯示ITLBO-ELM模型能夠對城市自來水供水量進行良好預測。

1 改進的教與學優化算法（ITLBO）

1.1 原始TLBO算法

TLBO算法是受教學過程中老師教學和學生學習活動的啟發而提出的優化算法[12]，種群中老師和學生個體均為候選解。假設班級中共有n個個體，其中學習成績最好（即適應度最佳）的個體被當作老師，其余的為學生個體。TLBO具體實現過程如下[13-14]。

（1）種群初始化。假設優化問題的解空間為s維，將種群中任意個體Xi=（xi1，xi2，…，xis）采用隨機方式進行初始化：

1.2 ITLBO算法

研究表明，標準TLBO算法在處理部分復雜優化問題時會因陷入局部最優而表現不佳。為了解決這一問題，提出一種改進的TLBO算法（ITLBO）。在ITLBO中，通過增加一個對最差學生補習階段和一種干擾策略，以增強算法快速收斂和跳出局部最優的能力。

在TLBO尋優過程中，增加一個最差學生補習階段，針對班級中學習成績最差的學生，通過老師單獨對該學生進行輔導，快速提升學生知識;在此基礎上，采用一種干擾算子對老師進行擾動，增強種群跳出局部最優的動能。

2.2 預測模型

ELM模型僅需要一步計算就可求出模型參數，即模型的輸出權值β-，此時ELM模型就完成了訓練過程。工程實際應用中往往因缺乏經驗而隨機給定輸入權重和隱層閾值，這將影響ELM模型的預測性能。為建立準確的自來水供水量預測模型，筆者提出采用ITLBO算法對ELM模型的輸入權重和隱層閾值進行優化選擇，在獲得最佳的模型參數基礎上建立ITLBO-ELM自來水供水量預測模型。ITLBO算法調整ELM模型參數核心思想是將城市供水樣本數據作為ITLBO-ELM模型的輸入值，ITLBO-ELM模型輸出供水預測值，將預測值與實測值進行對比，ITLBO通過預測誤差調整ELM模型參數，直到誤差降到允許值為止。

3 仿真實驗

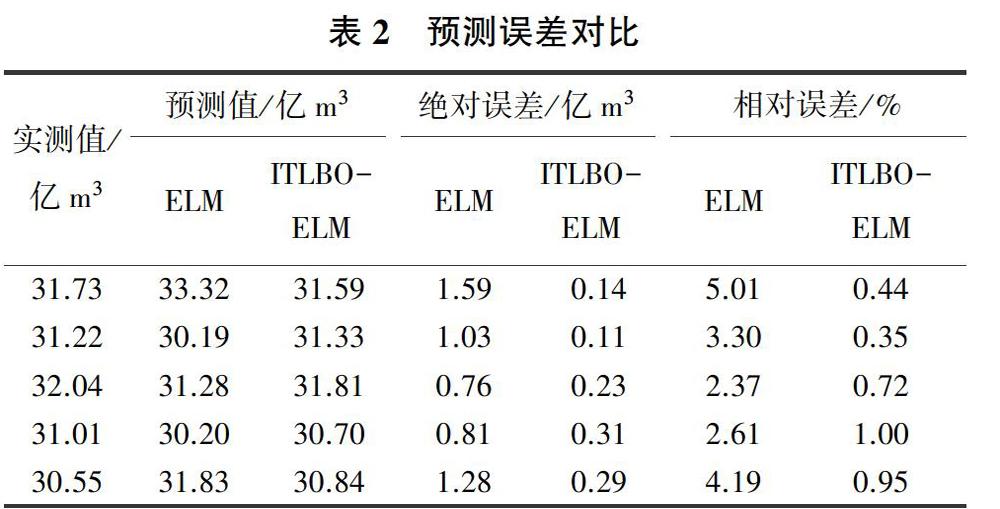
為驗證ITLBO-ELM模型的有效性，以上海市自來水供水量為研究對象，對自來水年供水總量進行預測。表1為上海市統計年鑒1980—2018年自來水供水總量統計數據。選取序號1～30的樣本數據用來訓練ITLBO-ELM模型，余下的樣本數據用來測試模型的泛化性能。自來水供水量預測結果見圖2，可以看出：ELM預測曲線和ITLBO-ELM預測曲線幾乎重合，均能對自來水供水量做出較好預測，但ITLBO-ELM模型預測精度優于ELM模型。表2為兩種模型的性能指標對比，可以看出：ITLBO-ELM模型的絕對誤差和相對誤差明顯小于ELM模型的。可見，經過ITLBO算法優化的ELM模型性能更優，能夠更好地預測城市自來水供水量。

4 結 論

城市自來水供水量預測對于優化水資源調度以及供水管網安全穩定運行具有重要意義。本文提出了一種優化ELM模型的自來水供水量預測模型，通過改進的ITLBO算法優化選擇模型參數，提高自來水供水量預測模型精度。在ITLBO算法中，通過引入補習階段和反學習策略提升最差學生的成績，并采用干擾算子對老師位置進行干擾，進一步提升TLBO算法的全局優化性能。改進后ITLBO算法用于ELM模型參數選擇，并建立ITLBO-ELM預測模型，仿真結果驗證了該模型能夠較好地預測自來水供水總量。

參考文獻：

[1] LI Tianhong， YANG Songnan， TAN Mingxin. Simulation and Optimization of Water Supply and Demand Balance in Shenzhen：A System Dynamics Approach [J]. Journal of Cleaner Production， 2019， 207：882-893.

[2] 朱連勇，雷曉云，文靜. RBF神經網絡在阿拉爾墾區需水預測中的應用[J].人民黃河，2012，34（7）：59-60.

[3] 郭強，李文竹，劉心.貝葉斯BP神經網絡的區間需水預測方法[J].人民黃河，2018，40（12）：76-80.

[4] 牟天蔚，蔣白懿，沈丹玉.深度學習框架對城市日供水量預測的研究[J].人民黃河，2018，40（9）：58-62.

[5] HUANG Guangbin， ZHU Qinyu， CHEE-KHEONG Siew. Extreme Learning Machine： Theory and Applications[J]. Neurocomputing， 2006，70（1-3）：489-501.

[6] 邵良杉，李臣浩. 基于改進花粉算法的極限學習機分類模型[J].計算機工程與應用，2020，56（1）：172-179.

[7] ZHOU Zhiyu， CHEN Ji， ZHU Zefei. Regularization Incremental Extreme Learning Machine with Random Reduced Kernel for Regression[J]. Neurocomputing，2018，321（12）：72-81.

[8] LIU Xia，XU Lin. The Universal Consistency of Extreme Learning Machine[J]. Neurocomputing，2018，311（10）：176-182.

[9] RAO R V， SAVSANI V J， VAKHARIA D P. Teaching-Learning-Based Optimization：an Optimization Method for Continuous Non-linear Large Scale Problems[J]. Information Sciences，2012，183（1）：1-15.

[10] TSAI Hsing-Chih. Confined Teaching-Learning-Based Optimization with Variable Search Strategies for Continuous Optimization[J]. Information Sciences，2019，500：34-47.

[11] 畢曉君，潘鐵文.基于教與學優化算法的相關反饋圖像檢索[J].電子學報，2017，45（7）：1668-1676.

[12] ALOK Kumar Shukla， PRADEEP Singh， MANU Vardhan. An Adaptive Inertia Weight Teaching-Learning-Based Optimization Algorithm and its Applications[J]. Applied Mathematical Modelling，2020，77：309-326.

[13] 何杰光，彭志平，崔得龍，等.一種多反向學習的教與學優化算法[J].工程科學與技術，2019，51（6）：159-167.

[14] 李麗榮，楊坤，王培崇.融合頭腦風暴思想的教與學優化算法[J].計算機應用，2020，40（9）：2677-2682.

[15] 廖康，吳益平，李麟瑋，等.基于時間序列與GWO-ELM模型的滑坡位移預測[J].中南大學學報（自然科學版），2019，50（3）：619-626.

【責任編輯 張華興】