單像素相機內部元素對重構矩陣性能的影響

吳小龍 程濤 楊明

摘? 要：單像素相機測量矩陣易于硬件實現，但對于單像素相機測量矩陣內部元素的改變對重構矩陣性能影響的研究較少.對于該問題，通過改變0-1循環矩陣中1的位置以及行和列的數量，對由基于0-1循環矩陣的重構矩陣優化得到的優化矩陣和近似矩陣進行分析來判斷重構矩陣的性能.實驗結果表明：基于改變后的0-1循環矩陣得到的重構矩陣、優化矩陣和近似矩陣對稀疏度為8～48的信號的重構能力要比0-1循環矩陣中列數和移位步長都是偶數時提升至少15%.該方法使重構矩陣的重構性能達到了理想的狀態.

關鍵詞：單像素相機;內部元素;重構矩陣;移位步長;重構性能

中圖分類號：TP391.41;TB852.1? ? ? ? ? ? ? DOI：10.16375/j.cnki.cn45-1395/t.2021.01.011

0? ? 引言

壓縮感知理論的核心是能夠減少測量點數并精確或近似精確地恢復出原始信號[1-3].Rice大學基于壓縮感知理論提出的單像素相機系統具有一個很明顯的優勢就是多光譜波段成像，這是基于壓縮感知理論和數字微鏡器件（digital micromirror decive，DMD）以及光電探測器的硬件特性而來的[4-6].單像素相機系統是壓縮感知在成像方面的一個重要應用.與傳統的成像系統相比，它通過開發原始光信號的稀疏特性，在光電探測器檢測到光信號之前，使用特定的矩陣對光信號進行調制，將所測數據導入恢復算法中，并依靠同步控制矩陣來重構圖像.它不僅打破了奈奎斯特采樣定理的局限，也打破了傳統的系統只能在局部波段進行成像的限制，為現在某些波段陣列傳感器價格昂貴、難以制備以及存儲成本高等問題提供了解決方案.

對于稀疏信號，不用再進行稀疏變換，可以通過行正交和列單位化對測量矩陣進行優化，盡管重建效果比較好，但是無法確定優化后測量矩陣的性質，因此，仍然存在硬件難以實現的問題.參考文獻[7]提出了一種用于稀疏信號的測量矩陣的優化算法，該算法在測量階段使用預先確定的測量矩陣來實現測量數據收集，在重建階段中使用優化后的矩陣來重建信號，取得了良好的效果.對于可壓縮信號，將信號作稀疏變換后，可以近似地將其當作稀疏信號.

上述研究更多是側重于測量矩陣與稀疏變換基之間的關聯，對測量矩陣本身的研究較少.本文通過改變0-1稀疏循環矩陣（簡稱0-1循環矩陣）中1的移位步長以及行和列的數量對重構矩陣以及由重構矩陣優化得到的優化矩陣和近似矩陣的性能進行分析，從而使重構矩陣的性能達到理想的狀態.

1? ? 壓縮感知理論與單像素相機

由文獻[8-10]可知，壓縮感知中，可壓縮信號模型如下：

其中：[x=ΨTα，? ΦR=ΦΨT].[y]是測量信號，[y∈RM];[Φ]是測量矩陣，[Φ∈RM×N]，[Ψ]是稀疏變換基，[Ψ∈RN×N];[x]是可壓縮信號，[x∈RN];[α]為[x]的稀疏變換域系數，[α∈RN];[ΦR]為重構矩陣.壓縮感知的核心過程為數據采集和數據重構.在測量階段，通過測量矩陣[Φ]采集到測量數據[y];在重構階段，通過式（1）解算得到變換域系數[α]，從而求得信號[x].

圖1為單像素相機的實物圖，如圖所示，光束打到物體上，經過透鏡1的光匯集到DMD上，DMD將光經過透鏡2打到單點探測器上，探測器將同步信號的電壓值輸入采集卡，再通過電腦進行數據處理.單像素相機的核心是DMD，在DMD上，每個“1”狀態的微鏡表示光束可以經過透鏡打到探測器上，每個“0”狀態的微鏡表示光束不能打到探測器上.DMD按照設定好的序列進行翻轉，通過DMD上所有“1”狀態的微鏡的疊加得到的是一個觀測值，DMD翻轉a次就可以得到a個觀測值.每個測量值相當于壓縮感知中的測量矩陣[Φ]的一行與信號[x]的內積.當前DMD已經達到百萬級的像素，可用波長范圍覆蓋350 nm紫外到? ? 2 500 nm近紅外波段.

2? ?基于不同移位步長的0-1循環矩陣的重構矩陣優化前后的性能分析

DMD可以設定不同的序列，相應測量矩陣設定也不一樣.測量矩陣大致可以分為3類：隨機矩陣[11]、部分正交矩陣[12]、確定型矩陣[13].其中確定型矩陣易于硬件實現，即確定型矩陣中循環矩陣又是最容易硬件實現的，所以采用0-1循環矩陣當作測量矩陣.通過文獻[7]的測量矩陣優化算法，得到的優化和近似矩陣都具有更好的性能，可以很好地重構稀疏信號.因此，在文獻[7]的測量矩陣優化算法中加入離散余弦變換（discrete cosine transform，DCT）矩陣（稀疏變換基），即可變成適用于可壓縮信號的重構矩陣（即：測量矩陣與稀疏變換基相乘后得到的矩陣）優化算法：對測量矩陣[Φ]和稀疏變換基[Ψ]相乘后得到的重構矩陣[ΦR]做行正交規范化和列單位化運算n次（即：n次迭代，一般? ?n=100）后得到優化矩陣[ΦO];然后，通過[T]=[ΦOΦTR（ΦRΦTR）-1]求得過渡矩陣[T];最后，通過[T]求得近似矩陣[ΦT]=[TΦR].

0-1循環矩陣中初始行為若干個隨機分布的1，其余元素為0，每一行由前一行元素向右移位一定的步長得到.設置測量矩陣為128×256維，當首行放置32個隨機分布的1時，經過不同的移位步長得到的基于0-1循環矩陣的重構矩陣會有不同性質.經過計算，當移位步長為偶數時，重構矩陣的列最大相關系數均大于0.999 0;當移位步長為奇數時，重構矩陣的列最大相關系數會發生改變，移位步長取5時，重構矩陣的列最大相關系數較小，為0.879 4.

本文主要研究基于移位為2的0-1循環矩陣的重構矩陣和基于移位為5的0-1循環矩陣的重構矩陣及其優化和近似矩陣，共計6類，分別簡稱為：移位為2的重構矩陣、移位為2的優化矩陣、移位為2的近似矩陣、移位為5的重構矩陣、移位為5的優化矩陣、移位為5的近似矩陣.

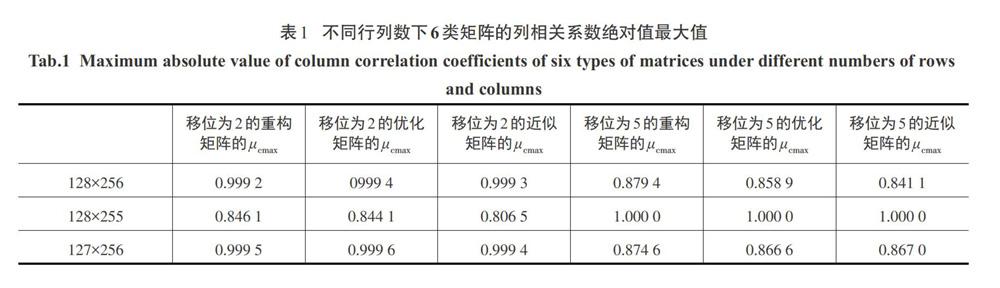
表1為不同行列數的測量矩陣分別采用移位為2的0-1循環矩陣和移位為5的0-1循環矩陣，稀疏變換基采用DCT矩陣，n=100時，相應重構矩陣、優化矩陣和近似矩陣的列相關系數絕對值的最大值[μcmax].

根據文獻[7]可知，經過行向量正交規范化和列向量單位化的優化矩陣和近似矩陣的性質與高斯矩陣相近，具備高斯矩陣[14-16]對各類稀疏信號的普適性.本文以此為依據，通過圖2—圖5分析基于移位為2的0-1循環矩陣和移位為5的0-1循環矩陣的重構矩陣在迭代優化過程中各自優化矩陣和近似矩陣性質的變化，圖2—圖5中測量矩陣均為128×256維，首行均放置32個隨機分布的1.

（a） 優化矩陣

（b） 近似矩陣

圖2中的參考線是縱坐標為[2]的水平線，由圖2（a）可以得知，基于移位為2的0-1循環矩陣的重構矩陣經過優化算法的迭代后，得到的優化矩陣行模的最大值在第30次迭代后收斂于參考線，最小值也在第30次迭代后收斂于參考線;基于移位為5的0-1循環矩陣的重構矩陣經過優化后得到的優化矩陣行模的最大值和最小值同樣在第30次迭代后收斂于參考線.由圖2（b）可知，基于移位為2的0-1循環矩陣的重構矩陣優化后得到的近似矩陣行模的最大值在第20次迭代后收斂于參考線，最小值在第90次迭代后收斂于1;基于移位為5的0-1循環矩陣的重構矩陣經過優化后得到的近似矩陣行模的最大值在第70次迭代后收斂于1.397 6，接近于參考線，最小值在第40次迭代后收斂于1.031 6.

（a） 優化矩陣

（b） 近似矩陣

由圖3（a）可知，基于移位為2的0-1循環矩陣的重構矩陣經過優化算法迭代后，得到的優化矩陣行相關系數的絕對值最大值在第10次迭代后收斂于0，列相關系數的絕對值最大值在第2次迭代后收斂于0.999 4;基于移位為5的0-1循環矩陣的重構矩陣經過優化得到的優化矩陣行相關系數的絕對值最大值在第10次迭代后收斂于0，列相關系數的絕對值最大值在第30次迭代后收斂于0.858 9.由圖3（b）可知，基于移位為2的0-1循環矩陣的重構矩陣經過優化后，得到的近似矩陣行相關系數的絕對值最大值在第60次迭代后收斂于0.209 3，列相關系數的絕對值最大值在第2次迭代后收斂于0.999 3;基于移位為5的0-1循環矩陣的重構矩陣經過優化后，得到的近似矩陣的行相關系數的絕對值最大值在第80次迭代后收斂于0.120 7，列相關系數絕對值最大值在第10次迭代后收斂? ? ? ? ? ?于0.841 1.

由圖4（a）可知，基于移位為2的0-1循環矩陣的重構矩陣經過優化算法后，得到的優化矩陣服從高斯分布的行由55迅速收斂于0，服從高斯分布的列由106迅速收斂于0;基于移位為5的0-1循環矩陣的重構矩陣經過優化得到的優化矩陣服從高斯分布的行由52次在第30次迭代后收斂于0，服從高斯分布的列由96在第30次迭代后收斂于0.由圖4（b）可知，基于移位為2的0-1循環矩陣的重構矩陣經過優化得到的近似矩陣服從高斯分布的行由55迅速收斂于0，服從高斯分布的列由106迅速收斂于0;基于移位為5的0-1循環矩陣的重構矩陣經過優化得到的近似矩陣服從高斯分布的行由52在第30次迭代后收斂于0，服從高斯分布的列由96在第30次迭代后收斂于0.

由圖5可知，基于移位為2的0-1循環矩陣的重構矩陣經過優化后得到的近似矩陣列模的最大值在第5次迭代后收斂于1.207 0，最小值在第5次迭代后收斂于0.070 3;基于移位為5的0-1循環矩陣經過優化得到近似矩陣列模的最大值在第5次迭代后收斂于1.2，最小值在第5次迭代后收斂于0.096 9.

通過分析圖2—圖5可知，隨著0-1循環矩陣移位的改變，其重構矩陣優化過程中優化矩陣和近似矩陣各參數最大的改變在于列相關系數的變化.基于移位為5的0-1循環矩陣，其重構矩陣以及優化后得到的優化矩陣和近似矩陣列不相關性好于基于移位為2的0-1循環矩陣的重構矩陣、優化矩陣和近似矩陣.

3? ? 基于不同移位步長與維數的0-1循環矩陣的重構矩陣理論分析

通過表1可以發現，當0-1循環矩陣的移位步長為偶數2時，矩陣行數不變，列數由偶數256變為奇數255后，基于移位為2的0-1循環矩陣的重構矩陣、優化矩陣、近似矩陣的列最大相關系數均減小至0.9以下;矩陣列數不變，行數由128變為127后，3種矩陣的列最大相關系數改變不大.當0-1循環矩陣的移位步長為奇數5時，矩陣的行數不變，列數由256變為255后，3種矩陣的列最大相關系數均變為1;矩陣列數不變，行數由128變為127后，3種矩陣列最大相關系數變化不大.

由上述分析可知，0-1循環矩陣的列數與移位要滿足不能同時為偶數或不能同時為奇數，此時重構矩陣的列不相關性可以達到較為理想的狀態，移位步長與0-1循環矩陣的行數無關.進一步分析可知，如果0-1循環矩陣的列數與移位均同時為奇數或同時為偶數，此時矩陣中的所有元素經過移位后均可以多次回到該列，導致0-1循環矩陣中列和列之間的相似度很大，因此，基于0-1循環矩陣的重構矩陣各列就會非常相似，失去了隨機性，即使對重構矩陣做優化也不能提高其隨機性，導致各列依然高度相關.

4? ? 基于不同移位步長的0-1循環矩陣的信號重構驗證

為進一步驗證循環重構矩陣及其優化和近似矩陣的性能，分別用移位為2的0-1循環重構矩陣和移位為5的0-1循環重構矩陣及其優化和近似矩陣對高斯稀疏信號采用正交匹配追蹤（orthogonal matching pursuit，OMP）算法[17-18]重構.OMP算法是一種經典的重構算法，其核心是依次對每一列元素進行重構.矩陣維數均為128×256，首行均放置32個隨機分布的1，對每個稀疏度的信號重復試驗500次，準確計算重構概率，如圖6所示，該實驗運用的軟件為MatlabR2014b.

由圖6可見，當測量矩陣為移位為5的0-1循環矩陣時，由其得到的重構矩陣、優化矩陣和近似矩陣的信號重構概率明顯好于基于移位為2的? ?0-1循環矩陣的重構矩陣、優化矩陣和近似矩陣的信號重構概率.稀疏度為8～48時，移位為5的重構矩陣、優化矩陣和近似矩陣的信號重構概率比移位為2的重構矩陣、優化矩陣和近似矩陣的信號重構概率均提升至少15%;當信號稀疏度為24時，3種矩陣的信號重構概率均提升了50%以上;當信號稀疏度小于16時，基于移位為5的0-1循環矩陣的重構矩陣、優化矩陣和近似矩陣的信號重構概率均接近于1.

5? ? 結論

單像素相機中DMD的設計直接關系到重構矩陣以及由重構矩陣優化得到的優化矩陣和近似矩陣的性能，以及DMD編程和機械實現的難易.0-1循環矩陣作為易于硬件實現的測量矩陣，其內部元素的設計非常重要，0-1循環矩陣的列數與移位步長要滿足不能同時為偶數或不能同時為奇數的要求，此時重構矩陣的列不相關性可以達到較為理想的狀態，移位步長與0-1循環矩陣的行數無關，按照該思路設計的測量矩陣可以大大增強重構矩陣以及優化矩陣和近似矩陣對信號的重構能力，這為單像素相機中DMD的設計提供了重要的參考.

參考文獻

[1] CANDES E J，PLAN Y. A probabilistic and RIPless theory of compressed sensing[J]. IEEE Transactions on Information Theory，2011，57（11）：7235-7254.

[2] CANDES E J，TAO T. Decoding by linear programming[J]. IEEE Transactions on Information Theory，2005，51（12）：4203-4215.

[3] 勞興松，李思敏，唐智靈. 大規模MIMO系統的貝葉斯匹配追蹤信道估計算法[J].廣西科技大學學報，2017，28（2）：8-16.

[4] KODAMA M，HARUYAMA S. Visible light communication using two different polarized DMD projectors for seamless location services[C]//Proceedings of the Fifth International Conference on Network，Communication and Computing，Kyoto，Japan，December 2016. Association for Computing Machinery，2016：272-276.

[5] VASILEIOS N，ZHAO S. Stronger L2/L2 compressed sensing;without iterating[C]// Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing，Phoenix，AZ，USA，June 2019. Association for Computing Machinery，2019： 289-297.

[6] 杜寶. 基于壓縮感知的平面近場聲全息理論與實驗研究[D].昆明：昆明理工大學，2017.

[7] 程濤，朱國賓，劉玉安. 基于0-1稀疏循環矩陣的測量矩陣分離研究[J].光學學報，2013，33（2）： 172-177.

[8] AHARON M，ELAD M. Sparse and redundant modeling of image content using an image-signature-dictionary[J].SIAM Journal on Imaging Sciences，2008，1（3）：228-247.

[9] BRUCKSTEIN A M，DONOHO D L，ELAD M. From sparse solutions of systems of equations to sparse modeling of signals and images[J].SIAM Review，2009，51（1）：34-81.

[10] 李春貴，陶佳偉，周愛霞. 基于鄰域能量的壓縮感知醫學圖像融合研究[J]. 廣西科技大學學報，2016，27（4）：15-20.

[11] UDDIN M N，ALVI S T，HOSSEN R，et al. Development of an effective cryptographic algorithm using random matrix shared key[C]//Proceedings of the 2019 3rd International Conference on Computer Science and Artificial Intelligence，Normal，USA，2019. Association for Computing Machinery，2019： 33-37.

[12] ZHANG W E，TAN M K，SHENG Q Z，et al. Efficient orthogonal non-negative matrix factorization over stiefel manifold[C]//Proceedings of the 25th ACM International on Conference on Information and Knowledge Management，Indianapolis，Indiana，USA，2016. Association for Computing Machinery，2016：1743-1752.

[13] GOLDREICH O，TAL A.Matrix rigidity of random toeplitz matrices[C]//Proceedings of the Forty-eighth Annual ACM Symposium on Theory of Computing，Cambridge，MA，USA，June 2016. Association for Computing Machinery，2016： 91-104.

[14] NEYKOV M，LIU J S，CAI T X. L1-regularized least squares for support recovery of high dimensional single index models with Gaussian designs[J]. Journal of Machine Learning Research，2016，17（1）：2976-3012.

[15] PAINSKY A，TISHBY N. Gaussian lower bound for the information bottleneck limit[J]. Journal of Machine Learning Research，2017，18（1）： 7908-7936.

[16] SUGIURA R，KAMAMOTO Y，HARADA N，et al. Optimal coding of generalized-Gaussian-distributed frequency spectra for low-delay audio coder with powered all-pole spectrum estimation[J].IEEE/ACM Transactions on Audio，Speech and Language Processing，2015，23（8）：1309-1321.

[17] NAKACHI T，KIYA H. Practical secure OMP computation and its application to image modeling [C]//Proceedings of the 2018 International Conference on Information Hiding and Image Processing，Manchester，United Kingdom，2018. Association for Computing Machinery，2018： 25-29.

[18] TROPP J A，GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory，2007，53（12）： 4655-4666.