基于K均值算法的X射線熒光光譜法檢驗藥用鋁塑包裝片的研究
劉金坤,李春宇,呂航,李飛,姜紅,滿吉
(1.中國人民公安大學 偵查學院,北京 100038;2.北京華儀宏盛技術有限公司,北京 100123)
藥用鋁塑包裝片是由鋁箔和聚氯乙烯(PVC)塑料泡罩組成的藥品包裝物,廣泛應用于膠囊藥品和片劑藥品的包裝[1]。在犯罪現場勘查過程中,藥用鋁塑包裝片是一種常見物證,通過檢驗其PVC塑料的類別,可縮小偵查范圍,為偵查和審判提供線索和依據。
法庭科學中,X射線熒光光譜法是塑料檢驗的常用方法[2-3]。本文收集到30種不同品牌、不同廠家的藥用鋁塑包裝片,用X射線熒光光譜儀測定每個樣品的元素含量。首先按照元素是否存在對樣品分組,對不確定組別的樣品用K均值算法聚類,運用誤差平方和法(SSE)確定最佳聚類簇數K,再用輪廓系數評估K值的有效性,得到了比較準確的分類結果。
1 實驗部分
1.1 材料與儀器
不同品牌不同廠家的藥用鋁塑包裝片聚氯乙烯(PVC)30個(部分樣品見表1);乙醇,分析純。

表1 藥用鋁塑包裝片樣品表Table 1 Medicinal aluminum-plastic packaging samples chart
X-MET8000 X射線熒光光譜儀(XRF);大面積SDD高分辨率半導體探測器。
1.2 實驗方法
藥用鋁塑包裝片表面沾有灰塵、油漬等雜質,需要對樣品進行簡單清洗,以保證測量數據的準確。在實驗測定之前,使用酒精棉對樣品進行擦拭,并將處理過的樣品晾干。用X射線熒光光譜儀分別測定樣品的元素含量,每種樣品實驗3次,取平均值。
2 結果與討論
2.1 XRF分析
X射線熒光光譜儀檢測結果見表2。
由表2可知,X射線熒光光譜測定的元素大多來源于PVC制作過程中的填料。其中,Cl元素含量最高,這是因為藥用鋁塑包裝片的主要成分是聚氯乙烯;Sn元素來自有機錫類穩定劑,如PVC制備過程中,為防止其熱分解,通常會加入二甲基氧化錫穩定劑;V元素來自釩的氧化物,有催化劑的作用;Cu元素主要來自塑料加工過程中的填料硫酸銅,具有良好的凝聚性,可以去除雜質;Zn、Ti元素主要來自常用金屬氧化物,有著色劑、增白劑的作用;Ba元素主要來自硫酸鋇,可以提高塑料熱穩定性,具有一定的潤滑性[4-7]。通過分析元素指標的來源,根據樣品中元素是否存在進行分組,結果見圖1。

表2 藥用鋁塑包裝片樣品X射線熒光分析結果(μg/g)Table 2 Analysis of medicinal aluminum-plastic packaging samples by XRF
由圖1可知,按照是否還有Ba元素進行分組時,19#樣品單獨分為一組,其他樣品分為另外一組。同理,將剩下的樣品按照是否含有Mn、Ti、Zn、V、Cu元素依次分組,最后將分組結果附上識別標簽,初步將30個樣品分為13組。其中,No.1,2,3,6,8僅含有一個樣品,得到了準確區分;No.12,13含有兩個樣品,用Pearson相關系數判斷其相關性,可以將兩個樣品區分;No.4,5,7,9,10,11含有3個及以上樣品,可根據K均值聚類法進行分類。
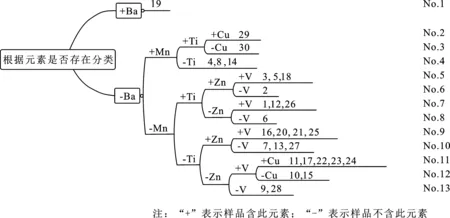
圖1 藥用鋁塑包裝片樣品分組圖Fig.1 Medicinal aluminum-plastic packaging samples sub-group chart
2.2 Pearson相關系數及假設檢驗
Pearson相關性分析是指對兩個或多個具備相關性特征元素進行分析,通過相關系數反映出特征元素間的相關關系[8],其表達式如下:
(1)
式中lXX——X的離均差平方和;
lYY——Y的離均差平方和;
lXY——X、Y間的離均差積和。
根據式(1)r值可判斷元素間的相關性,當|r|為0.00~0.19時,元素相關性極低;r=0.20~0.39時元素低度相關;0.40~0.69時中度相關;0.70~0.89時高度相關;0.90~1.00時相關性極高。
確定樣品的Pearson相關系數后,通過假設檢驗來判斷相關系數的有效性。假設檢驗首先提出假設,無關假設為H0,相關假設為H1。在統計學中,顯著性水平α通常設為0.05,當取得r值的概率0 由表3可知,No.12,13組的Pearson相關系數都接近于1,且P值遠小于0.05,相關性很強。通過比對鋁塑包裝片樣品表1可知,No.12組的10#和15#樣品、No.13組的9#和28#樣品分別屬于相同品牌、不同廠家的鋁塑包裝片,表明同一品牌的不用廠家生產鋁塑包裝片的材質差異較小。 表3 Pearson相關系數與假設檢驗Table 3 Pearson correlation coefficients and hypothesis tests K均值算法的思想是首先選定一個K值和K個初始類簇中心點,將樣品分別歸到離自己最近的簇中,然后重新計算每個簇的中心點,通過不斷迭代,當達到規定的迭代次數或者類簇中心點最小時,聚類完成[9]。通常情況下,K值的選擇有一定的不確定性,本文嘗試用誤差平方和法SSE來尋找K值[10],SSE的表達式如下: (2) 式中K——聚類數量; p——聚類樣品; mk——k個聚類的中心點。 由式(2)可知,隨著K值增大,每個聚類簇的聚合程度隨著增加,SSE的值慢慢減小;當K值接近真實聚類數時,再增加K所得到的聚合程度效果會迅速變小,SSE的下降幅度會驟減;當K值繼續增大時,SSE的下降幅度趨于平緩,那么最先趨于平緩的點就是合適的K值。 K均值聚類時選定No.11類藥用鋁塑包裝片樣品集(見表4),從Python語言的sklearn工具包中調用K-Means模塊,用Pycharm Community Edition實現代碼運行及數據分析[11]。 表4 No.11組藥用鋁塑包裝片樣品數據(μg/g)Table 4 No.11 medicinal aluminum-plastic packaging samples data 將 No.11組樣品數據傳入K-Means函數模塊,設定初始K值范圍1~6,調用SSE函數inertia,并調用matplotlib畫圖模塊展示SSE折線圖,見圖2。 圖2 SSE折線分布圖Fig.2 SSE line distribution 由圖2可知,當K值為1,2,3時,SSE的下降幅度驟減;K值為3,4時,折線走勢趨于平緩,故確定最佳K值為3。隨后,用K均值聚類算法進一步得到樣品分類結果,見表5。其中,1表示樣品屬于一類,0表示樣品不屬于一類,分類結果附上識別標簽。5個樣品中,22#、23#、24#被分成一類,11#和17# 單獨分為一類。 表5 No.11組樣品K均值算法分類表 標簽樣品編號1117222324100111210000301000 聚類效果的評估方法通常有輪廓系數、蘭德系數、互信息、Homogeneity、Fowlkes-Mallows scores、Calinski-Harabaz Index等[12],其中輪廓系數較為常用,當我們不能確定實際聚類類別時,可以通過輪廓系數來進一步評估[13]。單個樣品點Xi的輪廓系數表達式如下: (3) 式中,a為Xi與它同類別中其他樣品的平均距離;b為Xi與最近簇中所有樣品的平均距離。 通常情況下,用輪廓系數的平均值作為整個樣品集的輪廓系數值,取值范圍為[-1,1]。當同類樣品距離相近且不同類別樣品距離越遠,輪廓系數值就會增大,分類越合理。 在Python中,將K值傳入K-Means模塊,從sklearn工具包中調用元素指標驗證模塊metrics,再從metrics中引用silhouette-score函數。通過運算發現,當K為2時,S值為0.400,K為3時,S值為0.443,K為4時,S值為0.130。因此,當K值為3時分類效果最好,評價結果與聚類結果相一致,說明將SSE方法用于確定K值很有效。 根據此種方法將剩下的No.4,5,7,9,10組樣品繼續分類,得到了有效的聚類結果,見表6。其中,No.4,9組樣品分為兩類時輪廓系數S值較大,分類合理;No.5,7,10組樣品分2類時S值偏小,分3類時S值更小,故將組內樣品分為2類較為合理。 表6 樣品K均值聚類及輪廓系數評估Table 6 Sample K mean clustering and silhouette coefficient evaluation 采用X射線熒光光譜法結合統計學方法,實現了對藥用鋁塑包裝片的準確分類。實驗用X射線熒光光譜儀測定樣品元素含量,對樣品初步分組;對于只有一個樣品的組,不再繼續分類;有兩個樣品的組可根據Pearson相關系數分類;有3個以上樣品的組根據K均值算法分類,通過SSE方法確定K值并用輪廓系數評估分類結果,最終將藥用鋁塑包裝片樣品成功分類,達到預期的實驗結果。但本方法仍有需要改進的地方,比如樣品量應足夠多、模型更加簡化等。基于此,下一步將探索其他機器學習的分類算法,建立更加簡便的模型對樣品進行分類檢驗。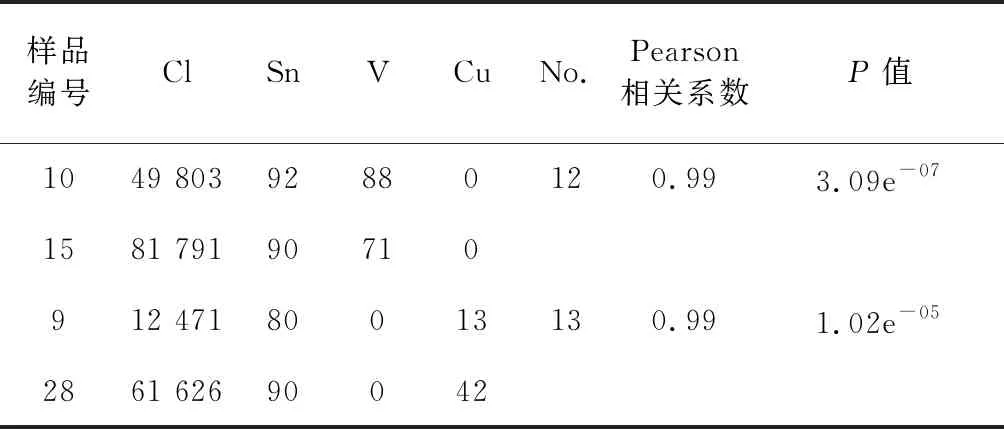
2.3 K均值算法

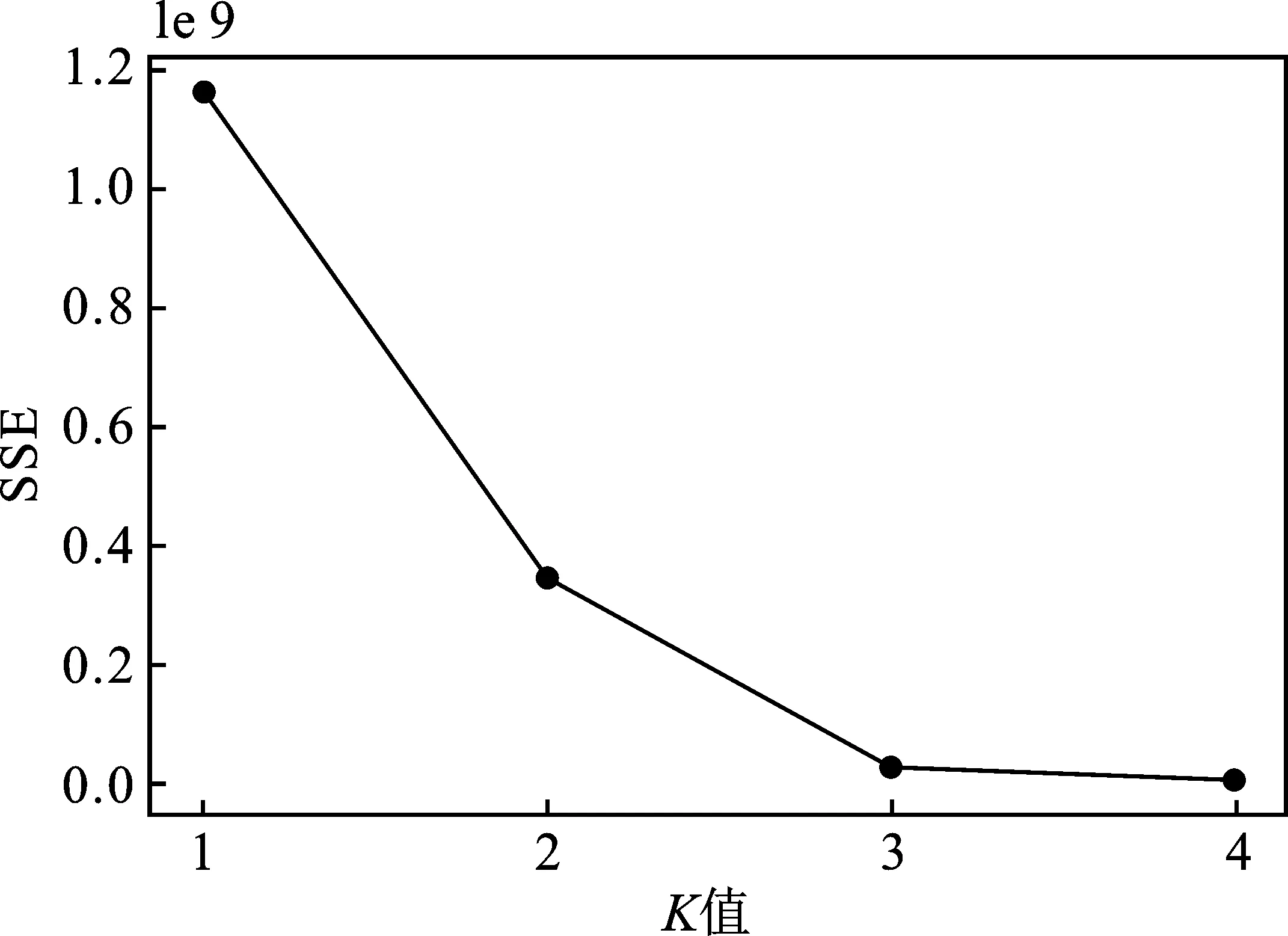
Table 5 No.11 samplesK-meansalgorithm classification table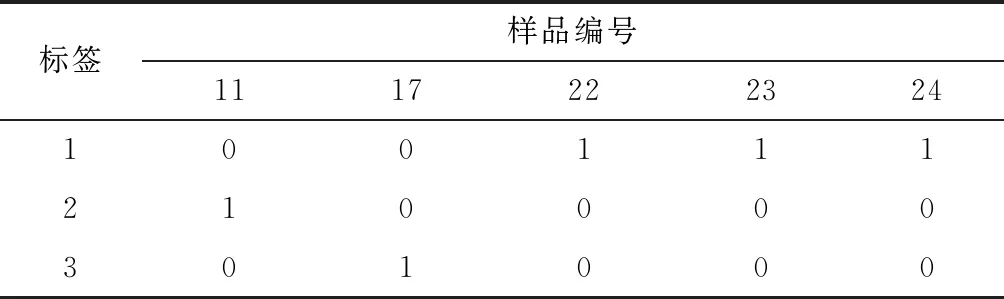
2.4 輪廓系數

3 結論

