主控參數對中低速磁浮列車軌道響應的影響

黃良煒 劉 放

西南交通大學 成都 610031

0 引言

隨著城市之間的交通狀況變得愈來愈復雜，中低速磁懸浮列車因為其整體懸浮在軌道上運行，避免了因軌道接觸產生的諸多問題，逐漸成為了城市軌道交通的新選擇。而列車運行時的振動響應，一直是磁懸浮軌道交通的研究重點。

趙春發等[1-4]對磁懸浮車輛進行了大量的研究，分別以德國Emsland磁懸浮系統和德國Transrapid磁懸浮系統為原型，建立了磁懸浮列車的車/橋耦合動力學模型和高速磁懸浮車輛的車/軌垂向耦合的動力學模型，分別分析了當磁懸浮系統在2種支承梁結構下運行時的動力學響應特征以及磁懸浮車輛的隨機振動響應。鄧永權等[5]建立了磁懸浮列車的動力學仿真模型，得到了利用仿真模型可以較為準確地預測磁懸浮車輛的實際運行情況的結論。鄒逸鵬等[7]將軌道高低不平順作為外部激勵輸入高速磁懸浮列車的垂向動力學模型，得到了高速磁懸浮車輛垂向動力學響應。徐飛等[8]分析了中低速磁懸浮列車的運用場景。蔣海波等[10]分析了線路不平順對磁懸浮列車動力學性能的影響，并得到了高頻和低頻時列車的運行狀況。陸海英等[11]以電磁懸浮中低速磁懸浮系統為原型，建立了磁浮列車的耦合系統動力學模型，對中低速磁懸浮列車起浮時的振動響應特性進行了深入研究，并對電磁懸浮中低速磁浮列車運行中的失穩現象提出了解決方案。王波等[13]分析了2種不同磁軌關系對中低速磁懸浮列車動力學性能的影響，并驗證了將懸浮控制模型替換為彈性阻尼模型的可行性。黎松奇等[14]對處于靜態懸浮狀態的磁懸浮列車進行了研究分析，并得到了車/軌的主要參數對列車垂向動力學響應的影響。

上述研究為工程實踐提供了一定的幫助，但在對磁懸浮列車的動力學響應進行分析時，并未考慮到電磁場的主動控制。本文將基于中國中低速磁懸浮列車建立列車的垂向動力學模型，并引入懸浮電磁場的主動控制，仿真分析在綜合考慮懸浮電磁場主動控制參數以及諧波軌道不平順激勵作為外部激勵輸入的情況下，中低速磁懸浮列車軌道響應的動態特性。

2 軌道不平順激勵分析

系統內部的自激振動以及外部的激擾振動是引起磁懸浮列車振動的2個主要來源。其中外部的激擾主要形式是軌道不平順。軌道不平順有多種類型，既包括具有隨機特征的不平順，也包括具有固定特征的局部不平順。本文的主要研究內容為磁懸浮列車的垂向動力學性能，故采用軌道的高低不平順作為輸入激勵來分析磁懸浮列車的垂向動力學性能。綜合考慮局部線路不平順的特征描述，認為其軌道高低不平順波形可表述為規則波形。用數學公式描述，可認為其不平順近似于正弦曲線，即

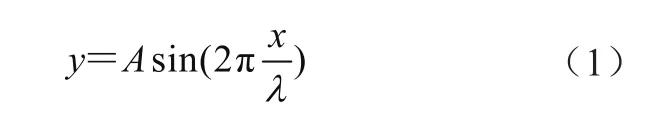
式中：A為諧波不平順幅值，λ為諧波不平順波長。

中低速磁懸浮列車系統對軌道線路的制造安裝精度要求一般在8 mm以下，故諧波不平順幅值取為8 mm。

3 動力學仿真模型建立

根據多體系統動力學理論，將磁懸浮列車各個部件均視為剛體，建立單節車輛的垂向動力學模型，由1個車體、5個懸浮架和20個電磁鐵共26個剛體組成。動力學仿真模型三維圖如圖1所示，簡化拓撲圖如圖2所示。

圖1 動力學仿真模型三維圖

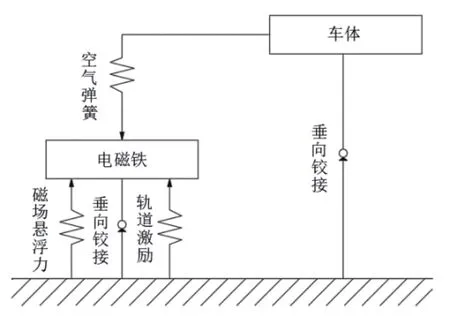
圖2 簡化拓撲圖

單節車輛垂向模型可以簡化為二自由度系統。假設各部件為剛體，得出磁浮車輛的垂向系統動力學方程為

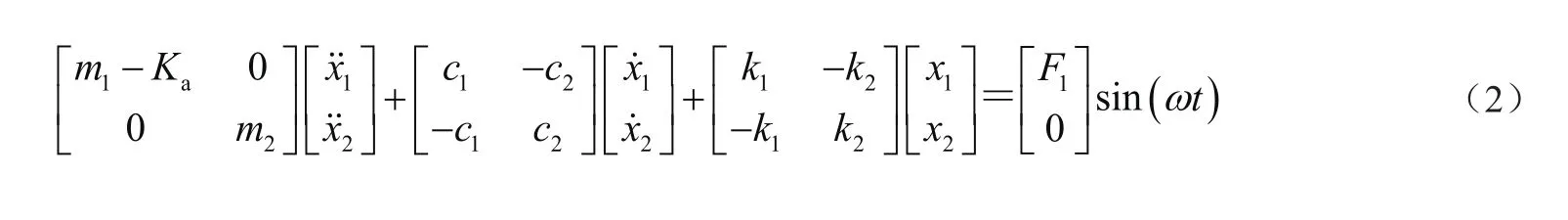
式中：m1、m2分別為電磁鐵、車體的質量總和，Ka是電磁場加速度反饋系數；x1、x2分別為電磁鐵、車體的垂向位移；k1、k2分別為控制懸浮電磁場、空氣彈簧的垂向剛度總和；c1、c2分別為控制懸浮電磁場、空氣彈簧的垂向阻尼總和；F1＝sin（ωt）為軌道高低不平順施加到電磁鐵上的激勵。

4 單因素對磁浮列車動力學性能的影響

本文首先針對電磁場模型中的3個參數K、Kv、Ka對列車搖頭，點頭以及側滾3個自由度角加速度的影響進行了單因素分析

4.1 K參數的影響

為了探究K參數對列車搖頭、點頭以及側滾3個自由度角加速度的影響，本文中在保持控制系數Kv和Ka不變的情況下，選取3組不同的K值進行了仿真試驗。其中K1～K3數值逐漸增大，截取列車運行平穩后的一段仿真結果，得到K參數分別對列車搖頭、點頭以及側滾3個自由度角加速度影響的結果圖，如圖3～圖5所示。由圖可知，K對于車輛的側滾角加速度的振動幅值有一定的抑制效果，但并未改變側滾角加速度的振動波形。此外K對于車輛的搖頭以及點頭角加速度影響并不顯著。

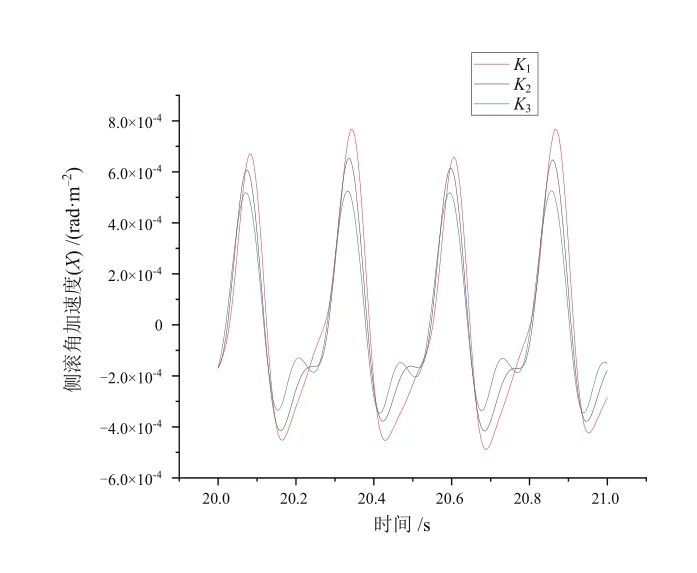
圖3 K參數對側滾角加速度的影響

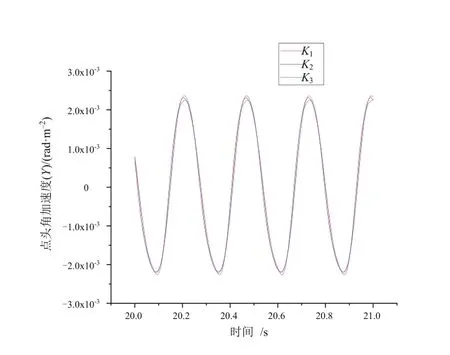
圖4 K參數對點頭角加速度的影響

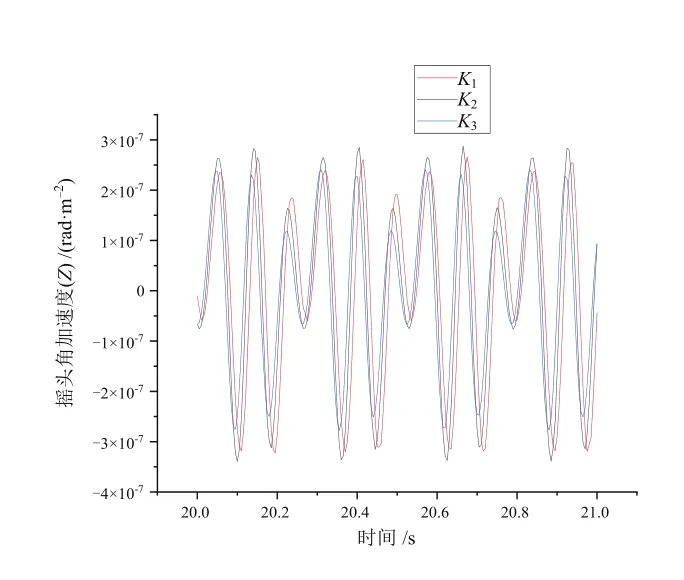
圖5 K參數對搖頭角加速度的影響

4.2 Kv參數的影響

與研究K參數過程相同，選取3組不同的Kv，Kv1～Kv3由0逐漸增大。仿真結果如圖6～圖8所示。Kv參數對于列車搖頭、點頭以及側滾3個自由度角加速度影響微乎其微。

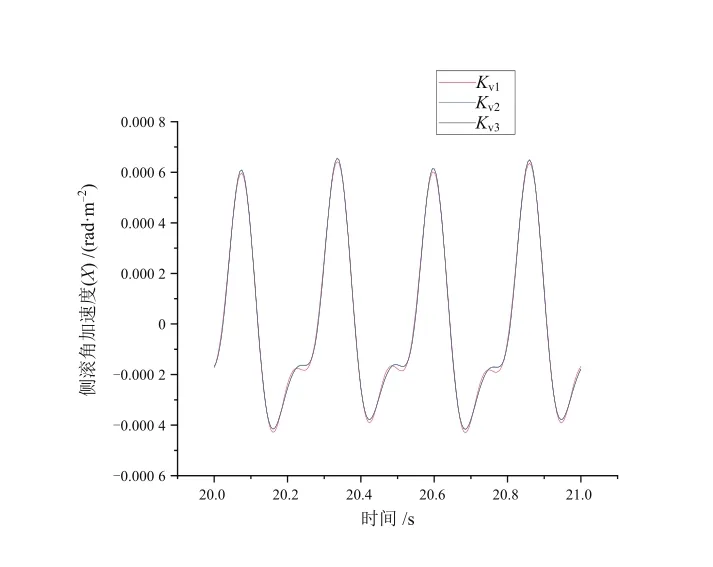
圖6 Kv參數對側滾角加速度的影響

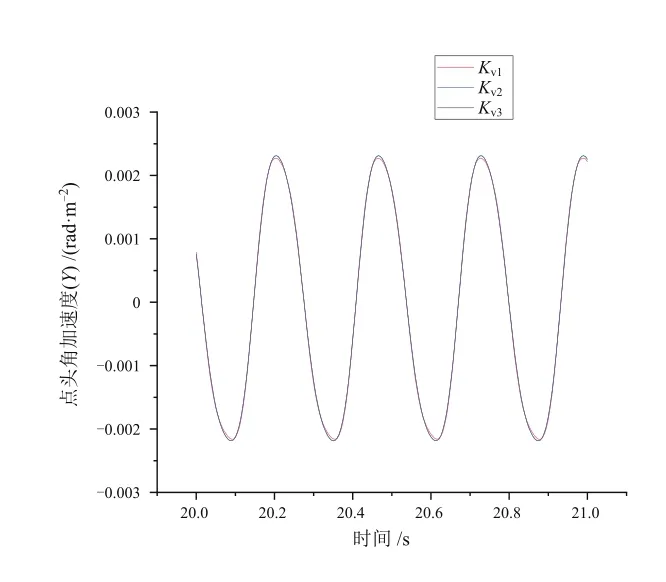
圖7 Kv參數對點頭角加速度的影響

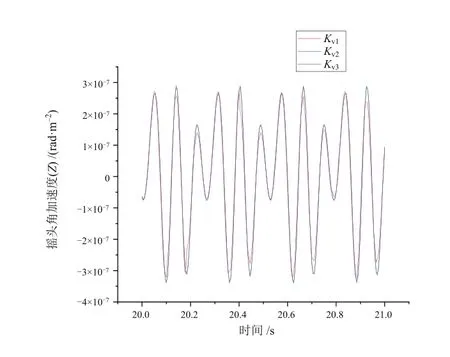
圖8 Kv參數對搖頭角加速度的影響

4.3 Ka參數的影響

與上述研究過程相同，選取3組不同的Ka，Ka1～Ka3由0逐漸增大，仿真結果如圖9～圖11所示。

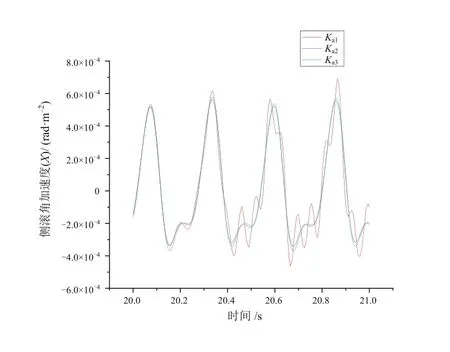
圖9 Ka參數對側滾角加速度的影響

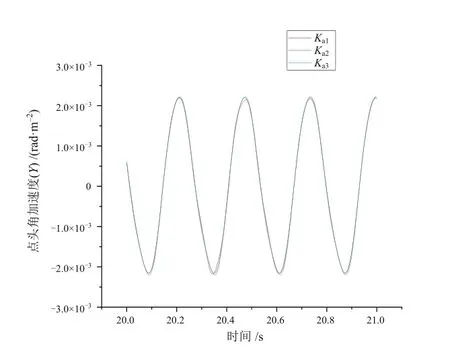
圖10 Ka參數對點頭角加速度的影響

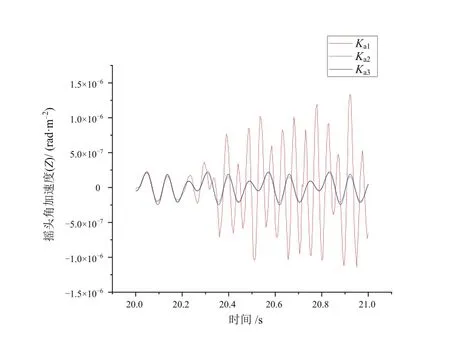
圖11 Ka參數對搖頭角加速度的影響

如圖9和圖11所示，由仿真結果可知，當Ka由0逐漸增大時，列車的側滾角加速度和搖頭角加速度的振動受抑制效果明顯。如圖10所示，列車的點頭角加速度并不受Ka參數變化的影響。

5 多因素對磁浮列車動力學性能的影響

根據前面單因素對動力學性能的影響分析可知，Kv參數對磁浮列車搖頭、點頭以及側滾3個自由度角加速度的影響微乎其微，故主要分析了K和Ka2個參數共同作用時對磁浮列車搖頭、點頭以及側滾3個自由度角加速度的影響，通過仿真試驗得到如圖12～圖14所示的仿真結果。

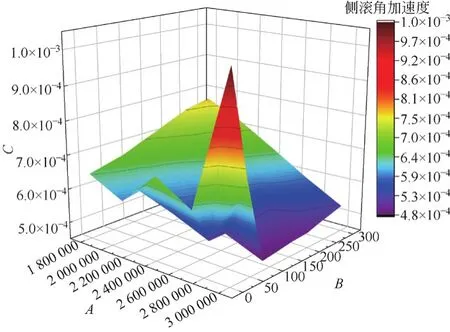
圖12 K和Ka共同作用時對側滾角加速度的影響

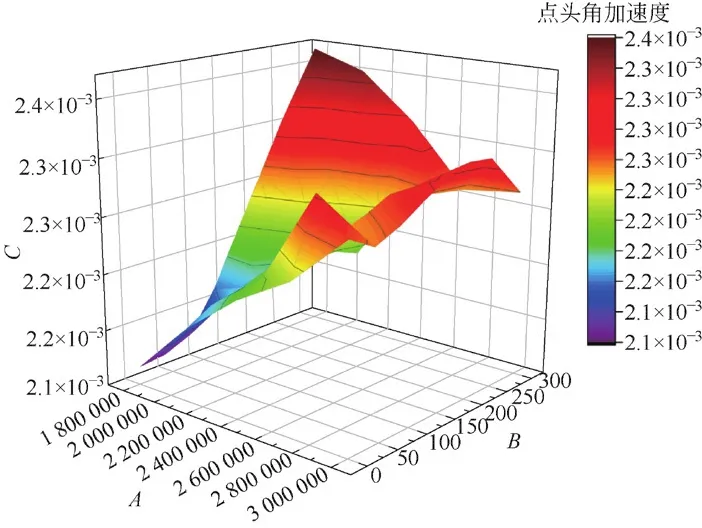
圖13 K和Ka共同作用時對點頭角加速度的影響

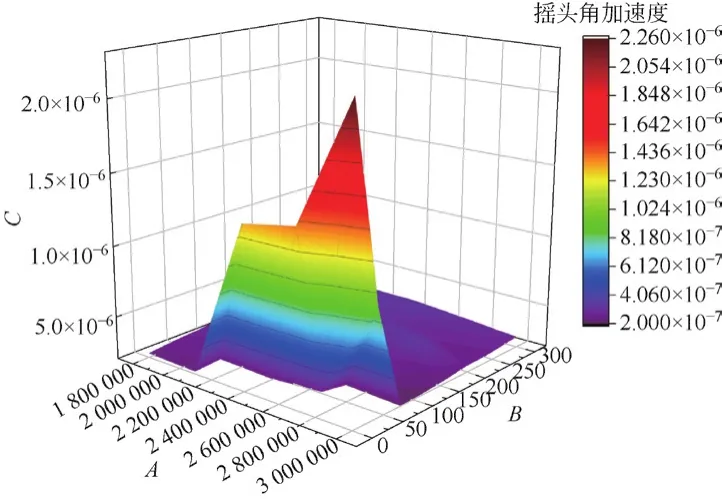
圖14 K和Ka共同作用時對搖頭角加速度的影響

由仿真結果可知，側滾以及搖頭角加速度峰值都出現在K最大、Ka最小的地方，而點頭角加速度則正好相反；當Ka值超過一個閾值后搖頭角加速度基本不會受到K和Ka參數變化的影響；對于點頭角加速度，曲面呈現出兩面高、中間相對低的現象；而側滾角加速度則表現為隨K的減小、Ka的增大逐漸增大的趨勢。綜上所述，為了得到相對較好的動力學響應，電磁場在進行主動控制的時候，使Ka值大于一個閾值的同時，K值以及Ka值均不宜過大也不宜過小，保持在適當的范圍為好。

6 結論

基于Simpack多體動力學仿真軟件建立了中低速磁懸浮列車的仿真模型，將軌道諧波不平順作為外部激勵輸入動力學仿真模型，分析了彈性阻尼系統中3個參數K、Kv、Ka對列車搖頭，點頭以及側滾3個自由度角加速度的影響，通過仿真分析得出以下結論：

1）參數K主要影響側滾以及搖頭角加速度的幅值，并未影響側滾以及搖頭角加速度的波形。對于參數Kv，3個自由度的角加速度基本不受Kv的影響。而參數Ka則主要影響側滾以及搖頭角加速度的波形。

2）參數K和參數Ka共同作用的時候，為了保證得到較好的列車動力學響應，電磁場進行主動控制的時候，參數K和參數Ka的調整應該適當，不宜過大也不宜過小。