抓住基本結構 任他千變萬化

文舒 芳

（作者單位：江蘇省無錫市西漳中學）

同學們，有一類基本圖形：三角形的兩條內角平分線交于一點，兩條外角平分線交于一點，或者一條內角平分線與一條外角平分線交于一點。圍繞這類圖的題靈活多變，角平分線還可以變為三等分線或者n等分線。但我們只要抓住基本原理，下次遇到也不用怕！

例題如圖1，在△ABC中，∠ABC與∠ACB的平分線相交于點P。

（1）如果∠A=80°，求∠BPC的度數；

（2）如圖2，作△ABC外角∠MBC、∠NCB的角平分線交于點Q，試探索∠Q與∠A之間的數量關系；

（3）如圖3，延長線段BP、QC交于點E，試探索∠E與∠A之間的數量關系。

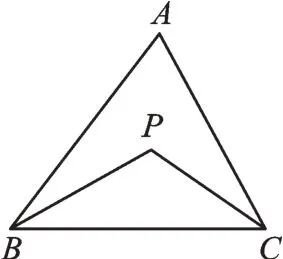
圖1

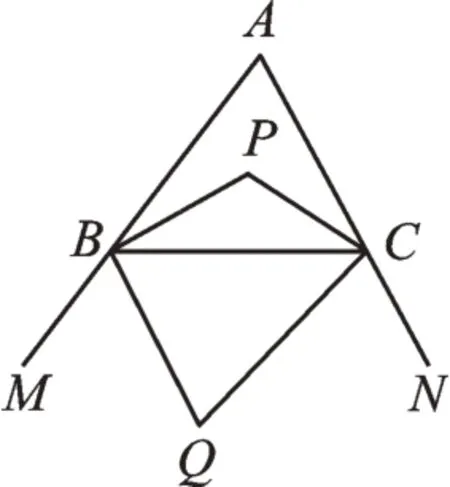
圖2

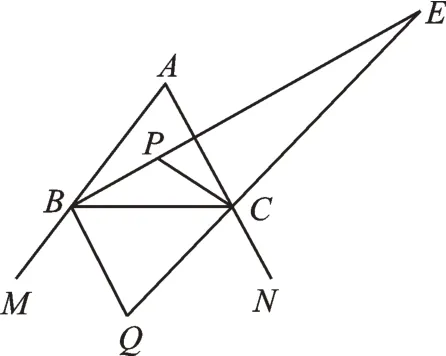
圖3

【錯誤】部分同學解答第（2）問時直接使用（1）中的條件“∠A=80°”，求出∠Q與∠A的具體度數，關系也沒有總結出來。

【錯因】審題不清，第（2）問慣性使用（1）中的條件；沒有具體的數據，就不會抽象分析，沒有真正領會“用字母表示數”的意義。

【解析】實際上，第（1）問可以把“∠A=80°”這個條件去掉，考慮一般的情況。“用字母表示數”，把∠A設為α°，運用三角形內角和定理表示∠ABC與∠ACB的和，再用角平分線的定義，求出∠PBC+∠PCB，進而求出∠BPC，獲得結論：∠BPC=90°+∠A。

第（2）問類似上面的思路，根據三角形的外角性質分別表示出∠MBC與∠BCN的和為360°-∠ABC-∠ACB，即180°+∠A，再根據角平分線的定義可求得∠CBQ+∠BCQ，最后根據三角形內角和定理即可求得∠BQC=90°-∠A。當然，在（1）知道∠BPC=90°+∠A的基礎上，我們還可以采用另一種方法。因為BP、BQ分別平分∠ABC、∠MBC，易證∠PBQ=90°，同理，∠PCQ=90°，最后利用四邊形BPCQ的 內 角 和 為360°，可 證 得∠BQC與∠BPC是互補的，問題也可解決。

第（3）問中，∠E是由三角形的一條內角平分線與一條外角平分線相交得來的。可以用三角形一個外角等于與它不相鄰的兩個內角和來解決。如圖4，延長BC至點F，∠3 是△BCE的外角，有∠E=∠3-∠1；∠ACF是△ABC的外角，有∠A=∠ACF-∠ABC；再根據角平分線的定義，∠3=∠ACF，∠1=∠ABC，可證得∠E=∠A。當然，也可由∠EBQ=90°知∠E與∠Q互余，進而獲得結論。

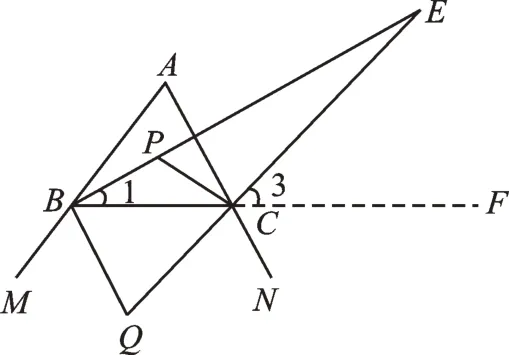
圖4

【總結】由三角形內角或外角平分線相交產生的角，其基本圖形和基本結論，我們可以總結成如圖5 的基本結構。其中最為重要的是對基本原理的掌握。

∠BPC是由△ABC的兩條內角平分線相交得來，則∠BPC=90°+∠A；

∠BQC是由△ABC的兩條外角平分線相交得來，則∠BQC＝90°-∠A；

∠E是由△ABC的一條內角平分線與一條外角平分線相交得來，則∠E=∠A。

【遷移】如圖6，∠MON=90°，在△ABO中，∠ABC=∠ABN，∠BAD=∠BAO，則∠D=______°（用含n的代數式表示）。

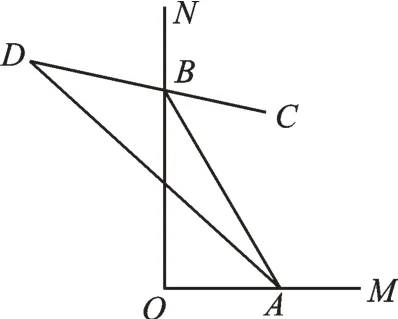
圖6

【解析】不難發現，∠D是由△ABO的一個外角n等分線與一個內角n等分線相交得來，我們可以將圖5 的基本原理遷移使用。因為∠ABN是△ABO的外角，有∠O=∠ABN-∠BAO；因為∠ABC是△ABD的 外 角，所以有∠D=