步進(jìn)電機(jī)的模糊控制研究

（廣東電網(wǎng)公司東莞供電局，廣東 東莞 523000）

0 引言

伺服電動(dòng)機(jī)或者步進(jìn)電動(dòng)機(jī)的共同點(diǎn)是提供了相似的精確定位，但是它們?cè)谠S多方面又有所不同。伺服電動(dòng)機(jī)需要模擬反饋控制系統(tǒng)，只能應(yīng)用于閉環(huán)回路。而步進(jìn)電機(jī)可用于簡(jiǎn)單的開環(huán)控制系統(tǒng)中。這些通常適用于在靜態(tài)負(fù)載下以低加速度運(yùn)行的系統(tǒng)，但是對(duì)于高加速度而言，尤其是在涉及可變負(fù)載的情況下，閉環(huán)控制是必不可少的[1]。

在本文中，提出了利用模糊控制邏輯的方法來控制步進(jìn)電機(jī)速度。Zadeh[2]提出閉環(huán)控制方案采用的是將設(shè)計(jì)人員的經(jīng)驗(yàn)與工程知識(shí)整合到自動(dòng)控制系統(tǒng)中以描述復(fù)雜的系統(tǒng)。但是這些系統(tǒng)很難使用傳統(tǒng)的數(shù)學(xué)方法進(jìn)行分析。實(shí)際上，Mamdani[3]是第一個(gè)設(shè)計(jì)出模糊邏輯在實(shí)驗(yàn)室小型蒸汽機(jī)中的應(yīng)用。這項(xiàng)研究的成功使許多科學(xué)家嘗試使用模糊算法來控制過程，例如化學(xué)反應(yīng)堆，自動(dòng)電機(jī)或核反應(yīng)堆的控制過程[4-5]。這些實(shí)驗(yàn)的結(jié)果表明，模糊控制器比傳統(tǒng)控制器的性能更好。而且，該技術(shù)的優(yōu)點(diǎn)是僅需一個(gè)簡(jiǎn)單的數(shù)學(xué)模型即可實(shí)現(xiàn)算法，該數(shù)學(xué)模型可通過數(shù)字計(jì)算機(jī)輕松實(shí)現(xiàn)。傳統(tǒng)的控制方法在工業(yè)環(huán)境中應(yīng)用廣泛，但對(duì)于大滯后、非線性復(fù)雜的系統(tǒng)，傳統(tǒng)常規(guī)控制方法的不穩(wěn)定性導(dǎo)致控制效果并不理想。模糊控制不需要控制對(duì)象的精確數(shù)學(xué)模型，它是一種基于規(guī)則的控制，更多的是依據(jù)操作人員的控制經(jīng)驗(yàn)，通過查表等方法，可以得到控制量，控制效果明顯。另外，模糊邏輯被研究者更頻繁地應(yīng)用于控制電機(jī)，例如直流電動(dòng)機(jī)或感應(yīng)電動(dòng)機(jī)[6]。然而，模糊邏輯的問題是它沒有專門用于模糊控制器設(shè)計(jì)的系統(tǒng)程序。正是由于這個(gè)原因，在本文中提出使用ANFIS（自適應(yīng)神經(jīng)模糊推理系統(tǒng)）的方法[7-8]來調(diào)整模糊系統(tǒng)的參數(shù)，從而達(dá)到對(duì)系統(tǒng)進(jìn)行控制的目的[9]。當(dāng)然，還有其他混合方法可用于獲得模糊系統(tǒng)[10]，但是，ANFIS是實(shí)現(xiàn)步進(jìn)電機(jī)控制過程中所需要的精度和效率的理想選擇。

1 步進(jìn)電機(jī)的分類

步進(jìn)電動(dòng)機(jī)分為永磁體和可變磁阻2 種類型，可變磁阻電動(dòng)機(jī)通常有3 個(gè)（有時(shí)是4 個(gè)）繞組，并具有相同的回路，而永磁電動(dòng)機(jī)通常具有2 個(gè)獨(dú)立的繞組，有的永磁電動(dòng)機(jī)還具有中心抽頭。中心抽頭繞組用于單極永磁電動(dòng)機(jī)[11]。步進(jìn)電機(jī)具有多種角度分辨率。

1.1 可變磁阻電動(dòng)機(jī)

如果電動(dòng)機(jī)具有3 個(gè)繞組，如圖1 所示。圖中所有繞組共有一個(gè)端子，則該電機(jī)為可變磁阻步進(jìn)電動(dòng)機(jī)。在使用的過程中，公共線通常與電源正極連接，并且繞組依次通電。圖1 所示的截面為可變磁阻電動(dòng)機(jī)的橫截面。該電動(dòng)機(jī)有4 個(gè)轉(zhuǎn)子，6 個(gè)定子，每個(gè)繞組都纏繞在2 個(gè)相對(duì)的磁極上。在給1 號(hào)繞組通電后，標(biāo)記為X 的轉(zhuǎn)子齒被吸引到該繞組的磁極上。如果關(guān)閉通過繞組1 的電流而打開繞組2 的電流，則轉(zhuǎn)子將順時(shí)針旋轉(zhuǎn)30°，以使標(biāo)記為Y 的磁極與標(biāo)記為2 的極對(duì)齊。

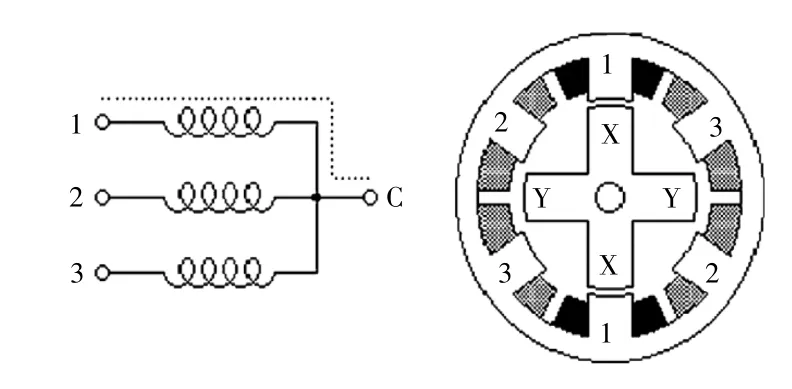
圖1 可變磁阻電動(dòng)機(jī)

1.2 單極電機(jī)

如圖2 所示，單極步進(jìn)電機(jī)（包括永磁體電機(jī)和5 或6 線混合步進(jìn)電機(jī)）通常為2 個(gè)繞組都有一個(gè)中心抽頭。在使用過程中，繞組的中心抽頭通常與電源正極相連，每個(gè)繞組的兩端交替接地，其目的是為了將繞組提供的磁場(chǎng)方向進(jìn)行翻轉(zhuǎn)。圖2 中所示的電動(dòng)機(jī)橫截面為30°每步的永磁電動(dòng)機(jī)。對(duì)于具有更高角度分辨率的電機(jī)，其轉(zhuǎn)子必須按比例具有更多的磁極與之相對(duì)應(yīng)。圖2 中的30°步進(jìn)電動(dòng)機(jī)是最常見的永磁電動(dòng)機(jī)設(shè)計(jì)之一，盡管15°和7.5°每步的步進(jìn)電動(dòng)機(jī)也被廣泛地使用。

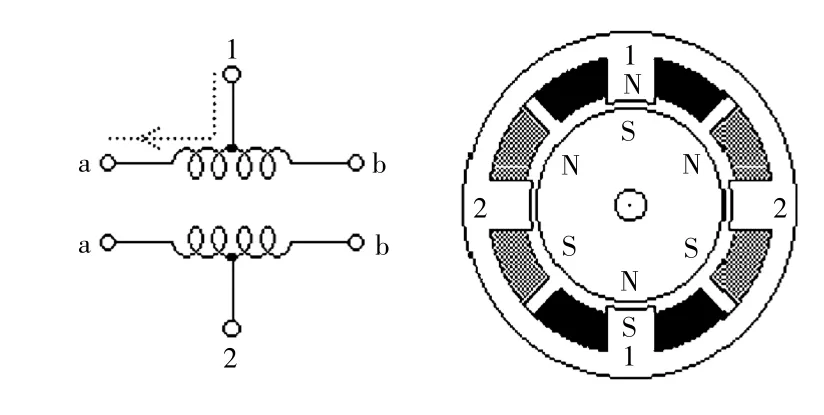
圖2 單相電機(jī)

1.3 雙極電機(jī)

雙極永磁體和混合動(dòng)力電動(dòng)機(jī)的結(jié)構(gòu)與單極電動(dòng)機(jī)完全相同，但是2 個(gè)繞組的接線方式更加簡(jiǎn)單并且沒有中心抽頭。圖3 顯示了這種電動(dòng)機(jī)的接線方式，電動(dòng)機(jī)橫截面與圖2 的橫截面完全相同。

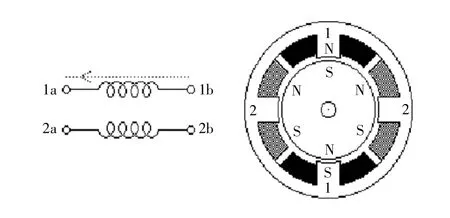
圖3 雙極電機(jī)

2 步進(jìn)電機(jī)的動(dòng)力學(xué)

每次步進(jìn)電動(dòng)機(jī)轉(zhuǎn)動(dòng)時(shí)，都要以電子的方式平移S 弧度。如圖4 所示，這會(huì)將整個(gè)曲線移動(dòng)了S 弧度的距離。

當(dāng)轉(zhuǎn)子從圖4 中的一個(gè)步驟到另一個(gè)步驟的一半時(shí)，最大可用轉(zhuǎn)矩達(dá)到最小值。該最小值是用來確定運(yùn)行轉(zhuǎn)矩，即確定電動(dòng)機(jī)緩慢前進(jìn)時(shí)可以驅(qū)動(dòng)的最大轉(zhuǎn)矩。如果通過一次給2 個(gè)繞組供電來驅(qū)動(dòng)步進(jìn)電動(dòng)機(jī)，則理想的兩繞組永磁電動(dòng)機(jī)的運(yùn)行轉(zhuǎn)矩將與單繞組轉(zhuǎn)矩保持一致。

電機(jī)轉(zhuǎn)子的共振頻率取決于振蕩的幅度。但是，隨著振幅的降低，諧振頻率上升到小振幅頻率。形式上，小幅度共振可以計(jì)算得到。首先，根據(jù)牛頓定律的角加速度可以得到：

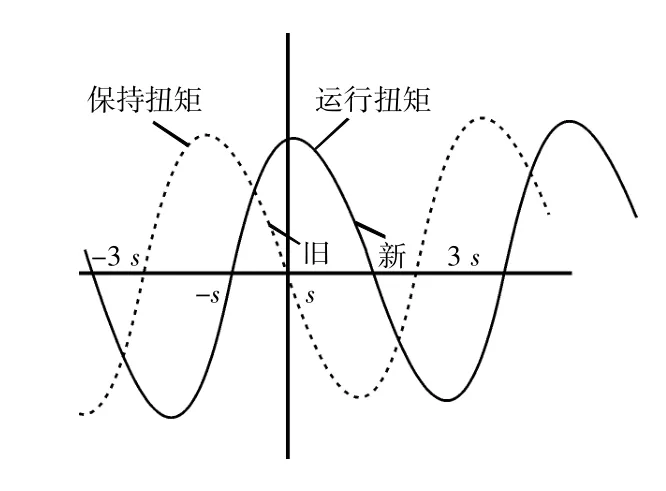
圖4 步進(jìn)電機(jī)的動(dòng)力學(xué)

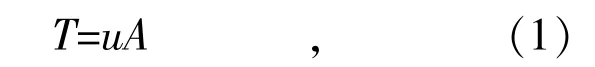
式中：T 為施加在轉(zhuǎn)子的轉(zhuǎn)矩；u 為轉(zhuǎn)子和負(fù)載的慣性矩；A 表示為角速度，A 以弧度每秒為單位。假設(shè)對(duì)于小振幅，轉(zhuǎn)子上的轉(zhuǎn)矩可以近似地表示為從平衡位置開始位移的線性函數(shù)，即：

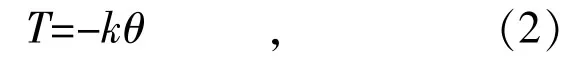
式中：k 為系統(tǒng)的彈簧常數(shù)，單位為每弧度的扭矩；θ 為轉(zhuǎn)子的角位置，以弧度為單位。

將獲得扭矩的2 個(gè)公式等價(jià)：uA=-kθ。加速度是位置相對(duì)于時(shí)間的二階導(dǎo)數(shù)：。因此，可以用微分方程形式將其轉(zhuǎn)換下形式為：。由f（t）=asinbt 得：

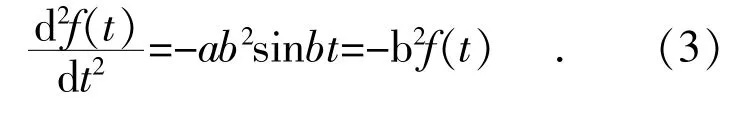
假設(shè)轉(zhuǎn)子共振，因此是在諧振的過程中，具有如下運(yùn)動(dòng)方程：

式中：a 為表示共振角幅度；f 為共振頻率。

實(shí)際上，當(dāng)步進(jìn)速率接近系統(tǒng)的諧振頻率時(shí)，這種振蕩會(huì)引起嚴(yán)重的問題。產(chǎn)生的后果為不可控制且隨機(jī)出現(xiàn)。

3 步進(jìn)電機(jī)的模糊邏輯控制

模糊邏輯控制器提供了一種算法，可以將基于專業(yè)知識(shí)的語言控制轉(zhuǎn)換為自動(dòng)控制策略從而達(dá)到控制電機(jī)運(yùn)轉(zhuǎn)的目的[12]。

根據(jù)實(shí)際數(shù)據(jù)，應(yīng)用ANFIS 方法來調(diào)整模糊控制器的參數(shù)[13-14]。PC 中會(huì)把生成步驟輸入到系統(tǒng)中并存儲(chǔ)。模糊控制器也包含在PC 中，并進(jìn)行相應(yīng)的響應(yīng)。實(shí)驗(yàn)系統(tǒng)如圖5 所示。

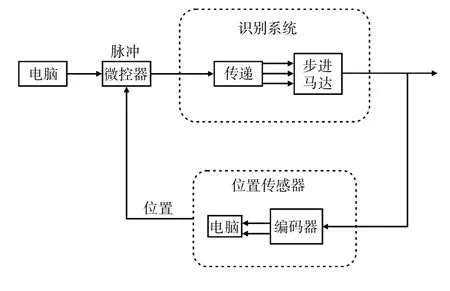
圖5 實(shí)驗(yàn)系統(tǒng)

（1）電動(dòng)機(jī)/驅(qū)動(dòng)器

微步電動(dòng)機(jī)型號(hào)為Vexta PV266-01E，具有5 個(gè)相數(shù)和500 步旋轉(zhuǎn)。電機(jī)如圖6 所示。具有多種分辨率的電源驅(qū)動(dòng)器Vexta DFR1514A（最低：500 步；最高：125 000 步）。

圖6 Vexta PV266-01E 步進(jìn)電機(jī)

（2）數(shù)據(jù)采集卡

采用研華PCL-818，具有8 個(gè)模擬輸入和2個(gè)模擬輸出（12 位），16 個(gè)數(shù)字輸入，16 個(gè)數(shù)字輸出，采樣時(shí)間為0.25 ms。

（3）計(jì)算機(jī)/軟件

控制規(guī)則如下：

用于控制步進(jìn)電機(jī)的Sugeno 模糊模型[15]。本文使用了ANFIS 方法來估計(jì)隸屬函數(shù)及其后繼函數(shù)的參數(shù)。對(duì)于每個(gè)語言變量，使用具有9 個(gè)規(guī)則和3 個(gè)隸屬函數(shù)的模糊模型。如圖7 所示，ANFIS 模糊系統(tǒng)的結(jié)構(gòu)，同時(shí)利用ANFIS 方法構(gòu)造顯示自動(dòng)設(shè)配網(wǎng)絡(luò)中的模糊控制，由ANFIS 方法生成的模糊規(guī)則如圖8 所示。這些規(guī)則是使用ANFIS 方法自動(dòng)生成的。該模糊模型的非線性面如圖9 所示。

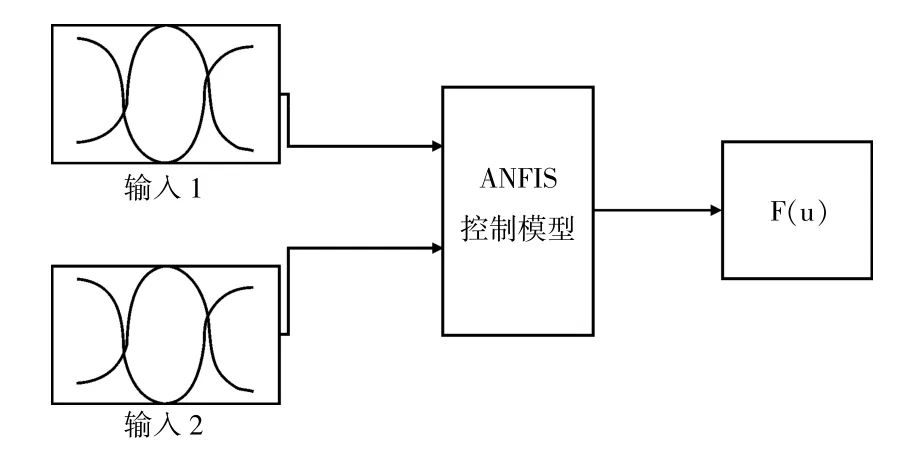
圖7 ANFIS 模糊系統(tǒng)的結(jié)構(gòu)

圖8 由ANFIS 方法生成的模糊規(guī)則

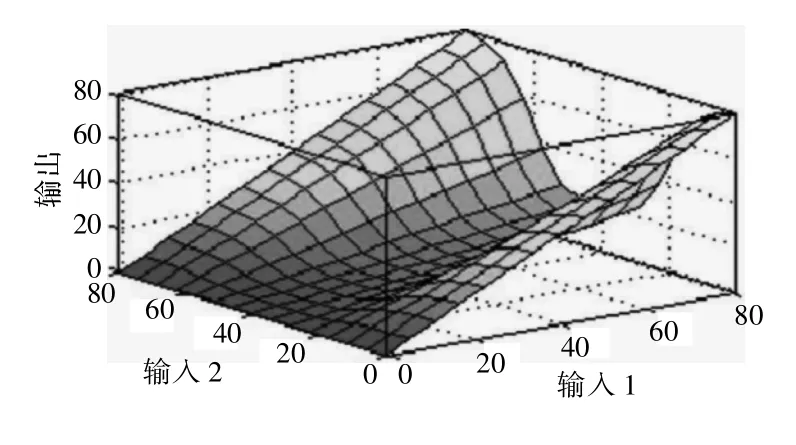
圖9 Sugeno 模糊模型的非線性表面

4 硬件的實(shí)現(xiàn)

模糊控制需要ANFIS 控制器才能真正實(shí)現(xiàn)智能步進(jìn)電機(jī)的目標(biāo)。神經(jīng)模糊方法使電動(dòng)機(jī)具備了適應(yīng)環(huán)境變化的能力。配備有智能控制器的步進(jìn)電機(jī)將能夠使用新數(shù)據(jù)對(duì)其進(jìn)行訓(xùn)練，并進(jìn)行數(shù)據(jù)參數(shù)的更新，從而能夠相應(yīng)地更改其行為。

ANFIS 方法的基礎(chǔ)訓(xùn)練是在自適應(yīng)網(wǎng)絡(luò)上進(jìn)行的，使用問題相關(guān)變量的時(shí)間序列作為數(shù)據(jù)。因此，選擇了Jstamp 微處理器作為控制器的核心。該微處理器使用JAVA 作為本機(jī)編程語言，具有512 KB 的RAM 內(nèi)存和512 KB 的FLASH內(nèi)存。如圖10 所示，為研究過程中的Jstamp 微處理器。由ANFIS 的數(shù)字混合性質(zhì)可知，在正向使用最小二乘法，而反向傳播算法是反向算法[16]。這些方法是用JAVA 語言實(shí)現(xiàn)的，然后將它們下載到Jstamp 微處理器中以獲得模糊控制器。

圖10 用于實(shí)現(xiàn)的Jstamp 微處理器

5 實(shí)驗(yàn)結(jié)果

如圖11 所示，表示為步進(jìn)電機(jī)對(duì)一系列步進(jìn)輸入信號(hào)的響應(yīng)（本方案使用了400 個(gè)樣本）。由圖12 可得到ANFIS 方法應(yīng)用于訓(xùn)練數(shù)據(jù)和測(cè)試數(shù)據(jù)的結(jié)果。使用了20 個(gè)紀(jì)元進(jìn)行訓(xùn)練，最終誤差為0.000 001，這對(duì)于此應(yīng)用程序非常有用。

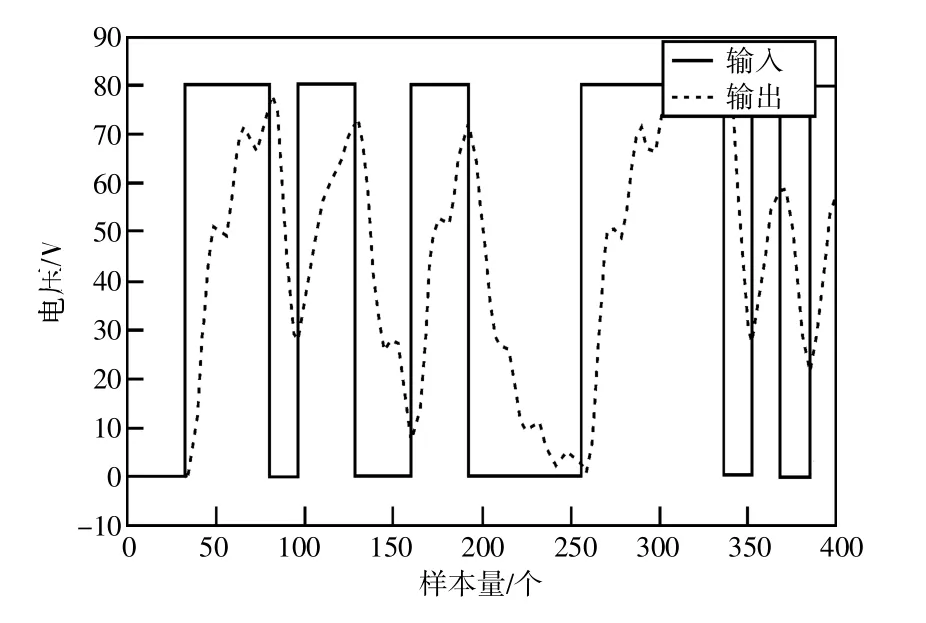
圖11 步進(jìn)電機(jī)對(duì)一系列步進(jìn)輸入信號(hào)的響應(yīng)

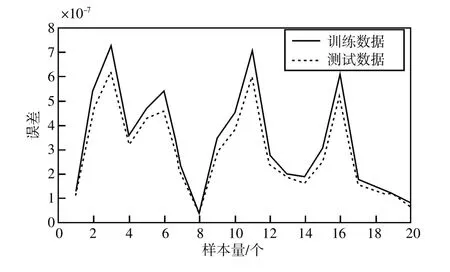
圖12 將ANFIS 方法應(yīng)用于訓(xùn)練和測(cè)試數(shù)據(jù)的結(jié)果

因此，所提出的設(shè)計(jì)證實(shí)了模糊控制與非線性過程的快速控制有關(guān)，例如步進(jìn)電機(jī)驅(qū)動(dòng)器中的定量方法并不總是合適的。與傳統(tǒng)的定量控制器相比，該方法的另一個(gè)優(yōu)點(diǎn)是不需要固定的采樣時(shí)間。

6 結(jié)語

本文通過仿真和實(shí)驗(yàn)證明了模糊控制在步進(jìn)電機(jī)驅(qū)動(dòng)中的可行性。通過使用ANFIS 確定了模糊控制器的最佳參數(shù)。模糊控制器具有非常強(qiáng)大的跟蹤功能，并且能夠響應(yīng)不同的動(dòng)態(tài)條件，模糊模型產(chǎn)生的數(shù)據(jù)非常接近實(shí)際值。