基于ZPD 理論的“常微分方程”變式教學
胡愛蓮
(喀什大學數學與統計學院,新疆喀什 844000)
0 引言
在大學本科數學“常微分方程”課程的教學過程中,經常遇到這樣的情況:有的學生在解微分方程變式問題時,苦苦思索卻不得其解,但經別人一指點,即刻恍然大悟。這說明學生頭腦中已經掌握了解決這個問題所必需的基本概念、基本理論和基本方法等知識,只是不知道如何運用這些概念、理論和方法去解決眼前的問題。于是便出現了這樣一個問題:怎樣掌握數學知識才有助于提高學生解決數學問題的能力?或者說,怎樣才能促進學生良好的數學思維與數學解題思維的有效建構?
1 ZPD 理論
蘇聯心理學家維果斯基提出的ZPD(The Zone of Proximal Development,最近發展區)理論認為,學生的發展有兩種水平:一種是學生的現有水平,指獨立活動時所能達到的解決問題的水平;另一種是學生可能的發展水平,也就是通過教師的教學所獲得的潛在水平。這兩種水平之間的差異就是ZPD(最近發展區),如圖1 所示[1].ZPD 理論科學地詮釋了在復雜的學習過程中教學的性質和形式,即:教學作為發揮潛在能力的支撐平臺,賦予學習者能力,為其解決問題和建構意義提供概念框架。在教學過程中,教師應首先對學習者的現有水平進行評估,據此設計超出其現有能力但又能發揮其潛在能力的教學內容和學習任務,幫助學習者超越當前發展區,進入更高水平的最近發展區。[2]因此,我們在進行大學本科數學專業課程教學時,僅僅把課本知識講清楚是不夠的,還應針對學生的最近發展區,針對課程知識結構一環套一環的邏輯性,在變式教學的設計上注意變式間的邏輯聯系,利用類比推理、化歸轉化等思想,預設“一題多變”“一題多解”的發散型變式和“一法多用”的聚合型變式,讓學生在現有的課程知識水平基礎上,通過教師教學過程中設計的一個個變式,逐步提高學生的ZPD,激發學生的學習興趣,挖掘學生的學習潛力,提高學生解決較高難度數學問題的能力,以更好地適應數學課程的學習。那么,在大學本科數學專業課程教學中,如何通過必要的教學方法和手段把邏輯抽象、結構嚴謹的數學知識轉化為易于調動其學習積極性、激發其潛能的能力,超越其最近發展區而達到下一發展階段的水平呢?這是值得廣大高校數學專業教師去實踐探究的問題。
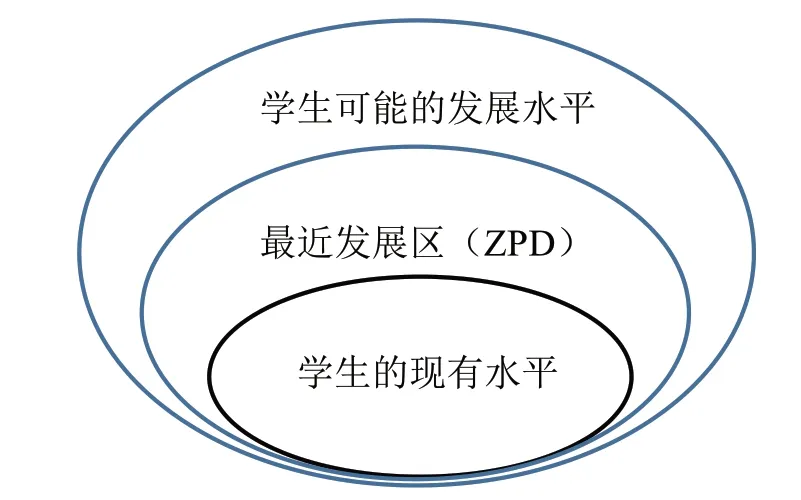
圖1 學生兩種發展水平及其差異間關系
2 基于ZPD 理論的“常微分方程”變式教學的具體實踐
2.1 一題多變增強學生解決問題的變通性
在維果茨基看來,僅僅依據學生的實際發展水平進行教育是保守、落后的,有效的教學應走在發展的前面去引導發展。因此,教育者不僅應該了解學生的實際發展水平,更重要的是要了解學生的潛在發展水平,尋找其最近發展區,把握“教學最佳期”以引導學生向著潛在的、最高的水平發展[3]。課堂上,教師從原問題出發,或橫向類比,或縱向深入,逐步引導學生完成預定的變式.對原問題、變式的設置要注意兩點[1]:(1)原問題的選擇既要簡單,符合學生現有的知識、能力、情感水平,能使學生通過問題認同自己的能力,有信心順利踏上發展的第一步;同時,原問題又要具有拓展性,可以是同一知識水平上的類比延伸,也可以是能深入挖掘的基礎題型.(2)各個變式的選擇要層層遞進、逐步深入,這樣才能讓學生在現有發展水平的基礎上,不斷向著最近發展區努力,以求順利地跨越當時的最近發展區,到達下一個最近發展區.
案例1從一階齊次方程
[4]的解法入手,縱向衍生出4個變式方程的解法。
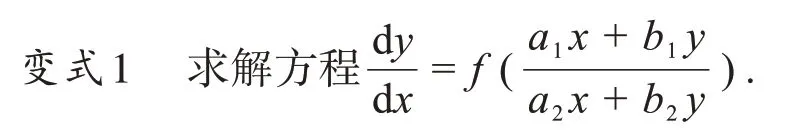
解析:此方程在原方程的基礎上做了擴展,a1=b2=0,b1=a2=1 時即為原問題。此時,右端函數中分式的分子、分母同除以x,則方程的右端就變成了變量的函數.
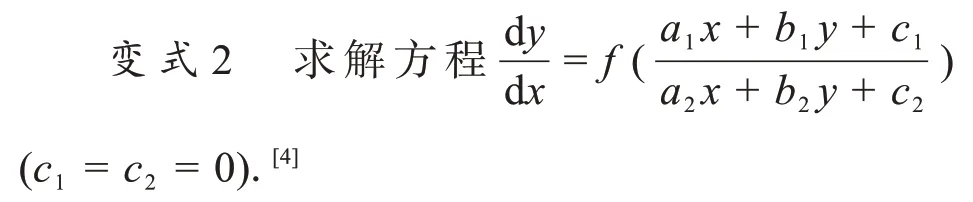
解析:此時就是變式1,變式2的設置起到了承上啟下的作用.


解析:此方程的右端函數為變量ax+by+c的函數,類似于原問題引入變量變換u=ax+by+c,可將方程化為變量可分離方程求解.
解析:此方程的右端函數中f為變量xy的函數,類似于原問題引入變量變換u=xy,可將方程化為變量可分離方程求解.

解析:此方程的右端函數中f為變量的函數,類似于原問題引入變量變換u=,可將方程化為變量可分離方程求解.
變式 4 求解方程f(xy)y+g(xy)xy′=0 (f(t)≠g(t)).
解析:此方程的左端函數中f,g為變量xy的函數,類似于原問題引入變量變換u=xy,可將方程化為變量可分離方程求解.
案例1 和案例2 將原問題1 從縱向、橫向兩個方面各產生了4個變式,都符合變式設置的兩個要求,由原問題到變式,難度在逐步加深,對學生的要求在逐漸提高,隨著變式教學的推進,學生從一個ZPD 發展到一個更高的ZPD,層層遞進,不斷引導和激勵學生,使其兩種發展水平呈螺旋式上升,最近發展區呈波浪狀前進.[5]
2.2 一題多解提升學生解決問題的能力
“常微分方程”各個知識板塊之間不是割裂的,相互之間存在著內在聯系.我們在學習一個新知識時,要注意建構新知識與已有知識間的聯系,把各個知識點聯系起來,引導學生逐步建立起屬于自己的知識結構體系,這樣學生就不再懼怕解決數學問題.而這種聯系,主要是靠“一題多解”來實現的。在已有知識儲備的前提下,通過用不同的方法解決同一問題,在這個過程中不斷尋找和建立新舊知識之間的內在聯系,既開拓了學生的數學思維、鞏固重構學生的知識結構體系,又可超越學生已有的最近發展區,達到下一發展階段的水平,進而提升學生解決數學問題的能力.
案例3通過問題2 的三種不同解法,演示如何通過一題多解提高學生的發展水平.


以上三種方法通過將方程進行適當的改寫,使其成為不同類型的一階顯示微分方程,再用相應方程的解法進行求解,導致了同一方程的不同解法。教師在教學中應引導學生主動思考,體會三種方法的本質,提高學生領悟數學本質的能力,同時也發展了學生的ZPD,利于其數學思維能力的提高.
2.3 一法多用激活學生解決問題的聚合性
基于ZPD 理論的常微分方程變式教學,僅僅停留在“一題多解”的發散型變式教學,可能會出現學生的數學思維得到了發散,但卻忽視了思維的聚合性,也就是要及時歸納總結各類方程的求解方法,促進學生數學思想方法系統性的形成.而常微分方程的“一法多用”的聚合型變式恰好能彌補這個缺憾.
“一法多用”型變式是將所要求解的結構形式不同的常微分方程進行局部調整,變成解法相同或類似的問題,這樣可以強化學生對某一種解法的掌握,同時,也以此為依據來解決其他問題.
案例4通過不同的一階微分方程改寫成微分形式,求得其積分因子,進而將原方程化為全微分方程進行求解.
原問題3 求解(y2+x2+x)dx+xydy=0.
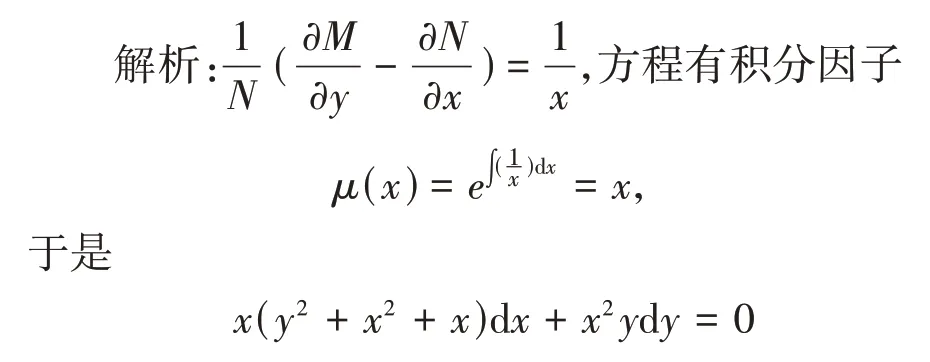

案例3的設置,可以讓學生體會到不同的一階顯式微分方程間的潛在關聯,從而歸納總結出解這一類題的通用解法——積分因子法,提升了學生的數學思維和解決問題的能力水平.
案例5常數變易法在不同微分方程(或方程組)的求解中的應用.
解析:此方程就是原問題2,其解法一就是常數變易法.

變式4 求解方程y˙+3y″+3y′ +y=[6].
解析:方程對應的齊次方程的特征方程為λ3+3λ2+3λ+1=0,解得λ1,2,3=-1,故對應的齊次方程的通解為

從案例3、4 可以看出,教師要引導學生對同一方法在不同問題中應用的重視,幫助學生尋求某一類題的常規通用解法,教學中要弱化針對性技巧,重視對一類問題通用解法的訓練.這樣不僅能達到觸類旁通、舉一反三的效果,還能拓寬學生的視野,啟發學生思維并提升學生數學思維能力,盡可能激發學生潛能,將學生的ZDP 提升到一個新的階段,使學生不斷在學習的過程中提高解決數學問題的能力.
3 總結
數學知識之間具有嚴密的邏輯性和知識的層層遞進,學生頭腦中形成的數學知識不是教師通過課堂訓練所形成的知識體系,而是學生通過主動思維在頭腦中對自己的理解進行建構而形成的。許多新的知識背后都有它所對應的原有基礎知識,教師在教學中要根據學生已有知識水平,在舊知和新知之間構建聯系的橋梁,激發學生對已學知識的再認識,激起學習對新知識的欲望,經過對新知識的遷移、發展形成下一個發展區。這就是創造最近發展區并使最近發展區轉化為現有發展水平的過程。遵循ZPD 理論的常微分方程變式教學能讓學生的最近發展區得到很好的發展,尤其是在課堂中有針對性的適度的運用變式教學,充分發揮學生的內在潛能,不僅能提升學生的思維水平,還能提高學生解決問題的能力,是一種切實可行的教學方法.

