Ground state cooling of an optomechanical resonator with double quantum interference processes?

Shuo Zhang(張碩), Tan Li(李坦),?, Qian-Hen Duan(段乾恒), Jian-Qi Zhang(張建奇), and Wan-Su Bao(鮑皖蘇),3,§

1Henan Key Laboratory of Quantum Information and Cryptography,SSF IEU,Zhengzhou,Henan 450001,China

2Innovation Academy for Precision Measurement Science and Technology,Wuhan 430071,China

3Synergetic Innovation Center of Quantum Information and Quantum Physics,University of Science and Technology of China,Hefei 230026,China

Keywords: laser cooling,coherent optical effects,multiphoton processes,optomechanics

1. Introduction

Over the last ten years, the study of macro- or nanomechanical resonators (MRs) have attracted considerable attention from both scientific and industrial communities. It results from the fact that the MRs hold a great potential for creating mesoscopic quantum states, developing novel quantum devices, and constructing highly sensitive sensors for metrology.[1–3]However, most of these applications are limited by the thermal phonons on the MRs for their low frequencies. Hence,cooling a MR to its ground state is a fundamental step towards its various applications.

To achieve the ground state cooling of the MRs,great efforts have been paid for searching different cooling methods,such as sideband cooling,[4–7]feedback cooling,[8]measurement cooling,[9]squeezed-light-based cooling,[10–12]and so on.[13]

In experiments, the well developed technology is based on the sideband cooling,[6,7]which can be realized by coupling a MR to a high quality optical cavity via radiation pressure coupling. With the assistance of the cavity dissipation and setting the system in the regime of the first-order red sideband,the MR can be cooled to its ground state in the resolved sideband regime, where the linewidth of the optical cavity is much smaller than the vibrational frequency of the MR.Moreover, to further reduce the thermal noise of the environment,the squeezed field is introduced to the sideband cooling, and the ground state cooling of the MR can be beyond the quantum backaction limit.[11]Nevertheless,limited by the manufacturing technology,the sideband cooling can only be realized by a few research groups.

On the other hand, to reduce the difficulty in the ground state cooling of the MR in the experiments, a variety of new cooling approaches based on quantum interference have been proposed in non-resolved sideband regime in which the linewidth of the optical cavity is larger than the vibrational frequency of the MR.These works for quantum inference cooling can be achieved with the assistance of coupled cavities,[14–16]superconductor systems,[17]quantum dots,[18–20]nitrogenvacancy (NV) centers,[21–24]and cavity quantum electrodynamics systems.[25–36]In these schemes, the internal degrees of freedom(d.o.f)works as a hybrid-multilevel configuration,and ground-state cooling can be achieved by the quantum interference effects, such as electromagnetically induced transparency(EIT)[37–39]and EIT-like effects.[40–42]Under the action of the quantum interference, the first red-sideband transition can be enhanced, while the one for blue-sideband will be suppressed,and the ground state cooling of the MR can be achieved in this way. As a result,it can be more efficient than the sideband cooling.

In this work, we present a scheme to cool a MR to its ground-state with two quantum interference processes. We assume an optomechanical cavity strongly couples to a tripod configuration atomic ensemble,and there is a double-quantum interference structure in the hybrid systems to improve the cooling performance. Then, we use the first quantum interference (EIT-like resonance) to enhance the narrow red sideband transition,and the mean phonon number of the MR can be cooled to the order of 1/CN, where CNis the cooperativity between cavity and atomic ensemble. Therefore, groundstate cooling can be achieved in strong atoms-cavity coupling regime.Moreover,to avoid the photon absorption by the atoms and provide a larger optomechanical coupling than previous atom-assisted cooling schemes,[25,26,28,31,32]the second quantum interference(cavity-EIT resonance)is introduced to cancel this process.As a result,the cooling rate of our scheme can be larger than relevant schemes, and it is more robust against heating caused by the thermal noise.

2. Model

2.1. Hamiltonian

The experimental setup is shown in Fig.1. An ensemble of N atoms is confined in an optomechanical cavity.[2]The vibrational frequency of the movable cavity mirror is ωm, and the cavity is pumped by an external laser field ?pwith frequency ωp. Each atom has one excited state |e〉 and three ground states |g〉, |r〉, and |s〉. The transition |e〉?|g〉 couples to a cavity field with single atom–cavity coupling strength g0[26]and frequency ωc, and the one between states |e〉 and|r〉(|s〉)is driven by the laser field ?r(?s)at frequency ωL1(ωL2).

Fig.1. (a) Experimental setup. An atomic ensemble is confined in an optomechanical cavity. The cavity is driven by a pump field. Each atom in ensemble simultaneously couples to two laser fields and the cavity field,as it is shown in panel(b).

In the rotating frame of frequencies ωp,ωL1,and ωL2,the Hamiltonian of the system is(ˉh=1)

Here,

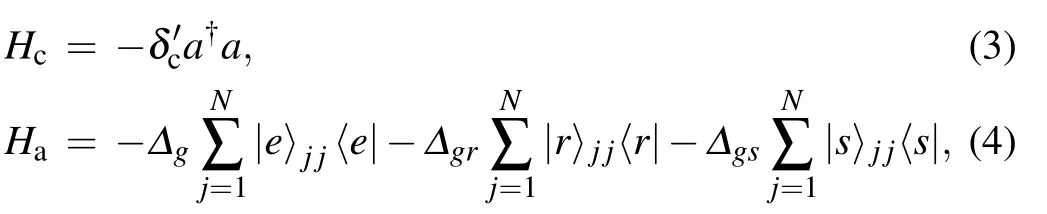
describe the effective energy of the MR, cavity mode and atoms, respectively. a (b) denotes the annihilation operator of the cavity(phonon)mode.

The corresponding detunings in Fig.1 are defined by

with ωeαbeing the transition frequency between states|e〉and|α〉for α =g,r,s.

The interaction Hamiltonian

is composed of

3. Results

3.1. Displaced frame and cooling processes

In the following, we would like to analyze the cooling dynamics with the displaced frame in Fig.2(a).[16]Assume that the internal state is initially in the state |1〉 =|NG,NE,NR,NS〉|nc〉, where Njindicates the Nj-th Fock state of the atomic ensemble excitation (j=G,E,R,S) and |nc〉(|nb〉) is the Fock states of cavity mode (the MR). The transition processes between the different states can be realized as the follows: the state |1〉|nb〉 can be coupled to states|2〉|nb±1〉 = |NG,NE,NR,NS〉|nc+1〉|nb±1〉 via the radiation pressure coupling λ, the transition from state |2〉 to state |3〉 = |NG,NE+1,NR,NS〉|nc〉 can be realized by the cavity-ensemble interaction gN, the state |3〉 can be transferred to states |4〉 = |NG,NE,NR+1,NS〉 |nc〉 and |5〉 =|NG,NE,NR,NS+1〉|nc〉 with laser fields ?rand ?s, respectively, and states |2〉 and |3〉 can dissipate to internal steady state|1〉with the atomic decay γ and cavity decay κ, respectively.

Fig.2. (a)The cooling dynamics in displaced frame. (b)The cooling dynamics can be reduced to transitions between the steady state and the first excited subspace.

Therefore,the internal d.o.f can be divided into the steady state|1〉and the first excited subspace M1spanned by states{|2〉,|3〉,|4〉,|5〉}.In this view,the Hamiltonian(12)should be rewritten as

with

3.2. Cooling conditions

which is the condition for the cavity-induced EIT resonance.In this situation,atoms are transparent to the cavity field,and the photon absorption vanishes. Therefore, the maximum of the optomechanical coupling strength λ is around ?gs= 0.Then the mean photon number of the cavity can be reduced to

Secondly, as shown in Refs. [29,44], the cooling coefficient A?can reach its maximum when Re{f(ωm)}=0. In our scheme,it can be easily achieved by choosing that

In the case of gN??r, the linewidth of |d〉 is 2γd=,which is much smaller than the natural linewidth of the cavity. Condition (25) ensures the red sideband transition is in resonance to the one for the narrow dressed states |1〉|nb〉→|d〉|nb?1〉,as shown in Fig.3(c).

Fig.3. (a) The interaction between states |2〉, |3〉, |4〉, and |5〉. Under the condition δc =?gr, an EIT-like quantum interference between transitions|2〉?|3〉and|5〉?|3〉.(b)The internal d.o.f can be diagonalized in dressed-state representation,including a narrow linewidth state|d〉. (c)By tuning ?gs=?ωm,the red sideband transition is resonant with the narrow resonance,and the cooling dynamics is analogous to resolved-sideband cooling.

In this situation,the cooling coefficient A?in Eq.(17)can be reduced to

Thirdly,one can find that the minimum value of A+is at

Condition (29) ensures a quantum destructive interference involving transitions |1〉|nb〉 →|2〉|nb+1〉 →|3〉|nb+1〉,|4〉|nb+1〉→|3〉|nb+1〉,and|5〉|nb+1〉→|3〉|nb+1〉,and A+is highly suppressed, which is similar to the optimal condition in double-EIT cooling scheme of a trapped ion.[39]

The combination of the optimal parameter conditions(23),(25),and(29)leads to

Then we can get a reduced cooling rate

and its corresponding final mean phonon number

4. Numerical simulations and discussion

To verify the validity of the optimal cooling conditions in the experiments,we choose the experimental parameters as follows:ωm=2π×1 MHz,λ0=2π×2.5 kHz or 2π×5 kHz,2κ = 2π ×10 MHz, N = 106, 2γ = 2π ×10 MHz, g0=2π×200 kHz,?p=2π×300 MHz ?r=?s=2π×50 MHz,and present some numerical calculations below.

The final phonon numbers as functions of detunings ?gr,δc,and ?gare plotted in Fig.4. According to the optimal parameter conditions(23),(25),and(29),the minimal final mean phonon number is at ?gr=δc=?ωmand ?g=?3750ωm. To find the optimal parameters for cooling with Fig.4,we choose the two optimal detunings in theory,and numerically simulate the final mean phonon number as a function of the third detuning.One can find that the optimal values of the third detunings coincide with analytical ones.

Fig.4. Numerical simulations of the final mean phonon number as functions of (a) ?gr, (b) δc, and (c) ?g. The parameters are ωm =2π ×1 MHz, λ0 = 2π ×2.5 kHz, 2κ = 2π ×10 MHz, N = 106,2γ =2π×10 MHz, g0 =2π×200 kHz, ?p =2π×300 MHz, ?r =?s=2π×50 MHz,δc=?ωm and ?g=?3750ωm for(a),?gr=?ωm and ?g=?3750ωm for(b),and ?gr =δc=?ωm for(c).

In Fig.5, we compare three-level atoms assisted cooling[26](red dashed lines) with four-level atoms assisted cooling (black solid line). The intracavity photon number|〈a〉|2, cooling rate W, and final mean phonon number nssas functions of ?grare plotted in Figs. 5(a)–5(c), respectively.From Figs.5(a)–5(c),we can find that intracavity photon number of four-level atoms assisted cooling is independent of ?gr,and the maximal cooling rate and minimal final mean phonon number are at the detuning ?gr=?ωm, as the above discussions. That is very different from the three-level atoms assisted cooling,where the maximum intracavity photon number and cooling rate are at ?gr=0,while the minimal final mean phonon number is at ?gr=?ωm. The simulations also show the cooling rate in our scheme is about one order of magnitude larger than three-level atoms assisted cooling.

Fig.5. The intracavity photon number |〈a〉|2 (a), cooling rate W (b)and final mean phonon number nss (c)as functions of ?gr for four-level atoms(black solid line)and three-level atoms(red dashed line).The parameters are ωm=2π×1 MHz,λ0=2π×5 kHz,2κ=2π×10 MHz,2γ =2π×10 MHz, gN =2π×200 MHz, ?p =2π×300 MHz, and δc =?ωm. For four-level atoms, ?gs =0, ?r =?s =2π×50 MHz,and the corresponding optimal detunings are ?g=?3750ωm and ?gr=?ωm;for three-level atoms,?r=2π×50 MHz,and the corresponding optimal detunings are ?g=?1250ωm and ?gr =?ωm.

Moreover,we would like to compare our scheme with the double-EIT cooling scheme.[39]Both of the cooling schemes are achieved by a double-EIT structure in four-level atom(s).In Ref. [39], the scheme is proposed to cool the motion of a trapped ion,and it use two EIT structure to eliminate the carrier and blue sideband heating transitions,respectively;while our scheme is ground state cooling of the MR,and it employ the first cavity-EIT structure to avoid photon absorption by atoms and the second EIT-like structure to generate a narrowlinewidth dressed state. Therefore,the cooling mechanism of our scheme is significantly different from Ref.[39].

Since the system always interacts with the environment,it is necessary to study the ground state cooling of the MR with different temperature. We plot the cooling result affected by the thermal noise in Fig.6. This simulation shows our scheme can cool the MR to its ground state nss＜1 at the temperature T ～50 mK and γm=10?5. Moreover,similar to Refs.[4,47],we also simulation the time evolution of mean phonon number〈n〉=〈b?b〉by numerically calculating the equation of motion of the arbitrary second-order moment in Fig.7. Figure 7 shows that the numerical simulation is in good agreement with the analytical solutions(16).

Fig.6.Numerical simulation of the final mean phonon number log10 nss as a function of T and γm. The parameters are ωm=2π×1 MHz,λ0=2π×5 kHz,2κ=2π×10 Hz,2γ=2π×10 MHz,gN=2π×200 MHz,?p=2π×300 MHz,and ?r=?s=2π×50 MHz.The black line corresponds to nss=1.

Fig.7. Numerical simulations of the mean phonon number n(t) for λ0=2π×5 kHz(red solid line)and λ0=2π×2.5 kHz(blue solid line).The dashed curves are their corresponding analytical prediction,respectively. The other parameters are ?p =2π×300 MHz, ?gs =0, ?gr =δc=?ωm,?g=?3750ωm,ωm=2π×1 MHz,gN =2π×200 MHz,?r =?s =2π×50 MHz, γ =κ =2π×10 MHz, γm =5×10?7ωm,and T =24 mK.

5. Conclusion

In conclusion, we have presented a ground state cooling scheme of a MR with the assistance of a four-level atomic ensemble. A better cooling result can be achieved by employing a double-quantum interference structures with different quantum interference processes. With the EIT-like quantum interference in atoms, the effective linewidth of the internal dressed state can be much smaller than the cavity linewidth,so that the cooling transition rate can be largely enhanced,while the heating transition is almost eliminated even in the non-resolved sideband regime. In addition, another quantum interference for the cavity induced transparency can be used to avoid photon absorption from atoms,a larger optomechanical coupling strength can be obtained, and a larger cooling rate can be achieved. As a result, this scheme can realize a faster cooling scheme than previous ones with the experimental parameters.