Dissipative preparation of multipartite Greenberger–Horne–Zeilinger states of Rydberg atoms?

Chong Yang(楊崇), Dong-Xiao Li(李冬嘯), and Xiao-Qiang Shao(邵曉強),?

1Center for Quantum Sciences and School of Physics,Northeast Normal University,Changchun 130024,China

2Center for Advanced Optoelectronic Functional Materials Research,and Key Laboratory for UV Light-Emitting Materials and Technology of Ministry of Education,Northeast Normal University,Changchun 130024,China

3School of Physics,International Joint Laboratory on Quantum Sensing and Quantum Metrology,Huazhong University of Science and Technology,Wuhan 430074,China

Keywords: multipartite entanglement,Lyapunov control,Rydberg antiblockade,quantum dissipation

1. Introduction

Quantum entanglement is one of the most remarkable features in quantum physics, as well as a valuable resource in the fields of quantum communication,[1–6]quantum computing,[7–12]and other quantum information processing.[13–22]With the development of quantum information science, bipartite entanglement has been intensively explored,and several milestones have been achieved.[23–25]In recent years,researchers have become increasingly interested in the study of multipartite entanglements.Compared with bipartite entanglement,multipartite entanglement can better reflect the nonlocality of quantum physics.[26]Greenberger–Horne–Zeilinger (GHZ) states represent a paradigmatic example of genuine multipartite entangled states. Because of the large information capacity, GHZ states have been used extensively in quantum secret sharing,[27–29]quantum teleportation,[30–32]and multipartite nonlocality tests.[33,34]Therefore,the generation and measurement of GHZ states with various systems and methods have become an attractive research field.

Rydberg atoms have been considered as a promising candidate among most applications of quantum information science.[35–41]The strong, long-range dipole–dipole or van der Waals interactions between Rydberg atoms will lead to the so-called Rydberg blockade effect, which suppresses the simultaneous excitation of two or more atoms into the same Rydberg state. Ever since the seminal scheme was proposed by Jaksch and coworkers,[42]a variety of proposals were designed for quantum information processing using the Rydberg blockade, such as quantum algorithms,[43,44]entanglement generation,[45–48]quantum repeaters,[49–51]singlephoton transistors.[52]In contrast to the blockade regime, the Rydberg antiblockade,which can achieve the simultaneous excitations of two Rydberg atoms, offers many new possibilities in the research of quantum logic gate[53–63]and quantum entanglement.[64–72]Quite recently, the authors of Ref. [73]provide a powerful approach for simulating quantum cellular automata and generating GHZ states with even numbers of particles restricted to nearest-neighbor interactions based on Rydberg antiblockade. Nevertheless, the next-nearest neighbor interaction of Rydberg atoms cannot be neglected within the parameters they consider,unless the case of three Rydberg atoms arranged in an equilateral triangle.[74]

To compensate for the defects in Refs. [73,74], we now design a more general strategy that can be used to produce GHZ states with both odd and even numbers of particles. This scheme is able to obtain the steady GHZ state in the presence of the next-nearest neighbor interaction by appropriately adjusting the frequency of the driving fields and the relevant detuning. Without loss of generality, we discuss in detail the preparation of GHZ states in three- and four-partite systems.The numerical simulation results show that the population of the target state in our scheme can reach more than 99%. In addition, we introduce external coherent control fields to accelerate the dissipative dynamics and widen the range of parameters, where the strength of the control fields is designed by the Lyapunov control theory. It is worth noting that the robustness of the optimized scheme against the spontaneous emissions of Rydberg states has also been greatly enhanced.

2. Preparation of tripartite GHZ state

2.1. Model

The system includes three identical Rydberg atoms,with each consisting of a ground state|g〉,a Rydberg state|r〉,and a temporary(short-lived)level|e〉. For simplicity,we just take three atoms arranged into an isosceles right triangle as an example (not limited to this specific alignment of atoms). The one at the right angle is atom 2,and the other two are labeled as atom 1 and atom 3. As shown in Fig.1,the transitions from the ground state|g〉to the Rydberg state|r〉of atom 1 and atom 3 are driven by the polychromatic fields ?1,2,4,5with detunings??1,2,4,5,while the polychromatic fields ?1,2,3with detunings??1,2,3are applied to drive the transition|g〉?|r〉of the atom 2. In addition,the resonant coupling between ground state|g〉and the short-lived state |e〉 is realized by the classical laser field of Rabi frequency ?0, and the atomic decay rate from the short-lived state|e〉to the ground state|g〉is Γ. Then the master equation of the whole system, after neglecting the decay of Rydberg states for the moment,can be expressed by the Lindblad form(assuming ˉh=1)

where the Hamiltonian in the interaction picture can be written as

Fig.1. The alignment and energy level structure diagram of three identical Rydberg atoms. |g〉, |r〉, and|e〉denote the ground state, the Rydberg excited state, and a temporary level, respectively. Here we have set the state |e〉 spontaneously decays into the ground state with rate Γ. For atoms 1 and 3, the transitions from|g〉to|r〉is realized by the polychromatic fields ?1,2,4,5,and the transition|g〉?|r〉of atom 2 is driven by the polychromatic fields ?1,2,3.In addition,the resonant transition|e〉?|r〉of the three Rydberg atoms is coupled to the classical laser of Rabi frequency ?0.

2.2. Optimization based on Lyapunov control

Lyapunov control is a sufficiently powerful control technique for quantum control tasks,[76–86]in which the key of the method is to select a series of appropriate Lyapunov functions.By designing the time-varying control fields, one can drive a quantum system to a target state or realize some specific operations. Based on Lyapunov control, we will optimize the above dissipative scheme to speed up the evolution to the target state and release the limiting conditions for the strengths of polychromatic driving fields. The general formula of quantum Lyapunov control to describe the evolution of system reads

with

where Hnare time-independent Hamiltonian corresponding to different types of external control, and fn(t) are the timevarying control fields established by Lyapunov function. Notice that the choice of Lyapunov function is not unique. In this paper, we consider the Lyapunov function in the following form:[87]

where ρtis the density matrix of the target state|GHZ?〉. Obviously, we can find that V(t) approaches a maximum value V(t)=1 as the system evolves into the target state. It is not hard to calculate that the first-order time derivative of V(t)is

Fig.3. Comparison with respect to the time-dependent population of state|GHZ?〉between the original scheme and optimized scheme.The populations are governed by Eqs.(1)and(8)containing the decay of Rydberg states,respectively. (a)[(d)]The population for target state versus the coupling strength ?1/?2 with γ =0 and Γ =6?2. (b)[(e)]The population for target state versus the decay rate Γ of the state|e〉with γ =0 and ?1=0.06?2. (c)[(f)]The population for target state versus the atomic spontaneous emission γ of Rydberg state with ?1=0.06?2 and Γ =6?2. The other parameters are chosen as ?0=0.8?2,?3=?5=0.06?2,?2=?4,and U =500?2.

For V to be a Lyapunov function, the control functions fn(t)should be chosen to satisfy ˙V(t)≥0. A simple and conventional way is to let[83]

3. Generalize to four-partite systems

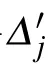
with

In order to investigate the optimization effect of Lyapunov control on this system, we plot the comparison diagram of the time-dependent population for target state|GHZ+〉versus the decay rate Γ, coupling strength ?1, and atomic spontaneous emission γ governed by Eqs. (12) and (16) in Fig.6,the coefficients λjare set as λ1= λ2= λ3= λ4= 0.1?2,λ5= λ6= λ7= λ8= 0.8?2, and the other parameters are consistent with those of Fig.5. Although the degree of acceleration is not as good as that of the three-partite system,the release of the constraint conditions and the robustness against the spontaneous emissions of Rydberg states are significantly enhanced.

Fig.6. Comparison with respect to the time-dependent population of state |GHZ+〉 between the original scheme and optimized scheme. The populations are simulated on the basis of Eqs.(12)and(16)by considering the spontaneous emissions of Rydberg states,respectively. (a)[(d)]The population for target state versus the coupling strength ?1/?2 with γ =0 and Γ =6?2. (b)[(e)]The population for target state versus the decay rate Γ of the state|e〉with γ =0 and ?1=0.05?2. (c)[(f)]The population for target state versus the atomic spontaneous emission γ of Rydberg state with ?1 =0.05?2 and Γ =6?2. The other parameters are chosen as ω1 =0.8?2, ω2 =ω3 =ω4 =0.24?2, ?2 =?3, ?4 =0.05?2 and U =300?2.

4. Experimental feasibility

Finally,we give some discussion on the experimental feasibility of our scheme. Our model is composed of Rydberg atoms arranged in different geometric shapes, which is a feasible technique in many experiments.[88–90]In Ref. [89], Nogrette et al. trap single87Rb atoms in the sites of arrays containing up to approximately 100 microtraps separated by distances as small as 3 μm, with geometries ranging from simple square or triangular lattices to more complex ones,such as kagome or honeycomb structures. Here we may employ87Rb with Rydberg state |r〉≡|80S1/2〉, and the corresponding Rydberg-Rydberg interaction is Urr=C6/r6,where C6=2π×4162.712 GHz·μm6.[75,91]We set the atomic distances in the three-particle system and four-particle system as r =4.502 μm and r =4.902 μm, and the corresponding strengths U are 2π×500 MHz and 2π×300 MHz, respectively.

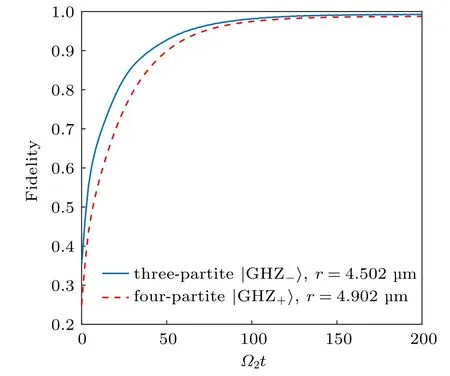
Fig.7. The fidelity of target state diagram simulated according to experimental parameters. The solid blue line and the dotted red line indicate the three-and four-particle system of optimized schemes,respectively. The initial states and other parameters of the three- and four-partite system in the numerical simulation are consistent with those in Figs.2 and 5,respectively.

5. Summary

In summary,we have systematically investigated the feasibility of preparing GHZ states in three-and four-partite systems by using Rydberg antiblockade and the engineered spontaneous emissions of Rydberg states in the presence of the next-nearest neighbor interaction of Rydberg atoms. The introduction of additional control fields according to Lyapunov control enables us to accelerate the dynamic evolution of the system, release the original constraints for the polychromatic driving fields, and enhance the robustness against the spontaneous decay of the excited Rydberg state. We hope that our work may provide a new prospect with regard to the dissipation-based quantum information processing of neutral atoms.