鋼_竹組合箱形柱的偏心受壓力學性能

茅 鳴，李玉順，劉 濤，張家亮

(1.寧波大學 土木與環境工程學院，浙江 寧波 315211；2.青島農業大學 建筑工程學院，山東 青島 266109)

中國竹資源豐富，竹材產量和儲蓄量較大.竹材低碳可再生，具有強度高、耐磨性好、性能穩定等特點.如今，隨著科技發展和工業化水平提高，對原竹材料進行改性加工，可制成適用于建筑領域且擁有強度高、韌性強、受力變形小、力學性能優良等諸多優點的竹材人造板[1]，而冷彎薄壁型鋼因其輕質高強、剛度大、截面成型靈活等特點被廣泛應用于建筑結構中.這2種材料可通過結構膠與自攻螺釘復合制作成梁、柱、樓板、墻體等鋼-竹組合構件，從而實現這2種材料的優勢互補[2-4].

柱是建筑結構中主要承重構件之一，柱的優劣直接影響到結構的受力性能.目前，研究較為成熟且應用較多的柱構件主要應用于鋼筋混凝土結構、型鋼混凝土結構、鋼管混凝土結構等[5-6]，對于竹材柱以及竹木復合構件也有一定的研究.魏洋等[7]、李海濤等[8-9]對重組竹柱進行偏心受壓試驗，提出了考慮偏心距影響系數的承載力計算公式；在此基礎上，王一博等[10]研究了重組竹中長柱雙向偏心受壓力學性能；Luna等[11]、劉常浩等[12]、Li[13]等和Huang等[14]分別對膠合竹柱進行軸心受壓、偏心受壓試驗研究，分析了長細比對軸壓試件力學性能的影響以及偏心距對偏壓試件力學性能的影響.

鋼-竹組合結構作為一種新型的結構體系，現階段對其研究和應用都較少.周靖等[15]、趙衛鋒等[16-17]將薄壁方鋼管與竹膠板粘制成組合空芯柱，對其進行軸壓、偏壓試驗，探討了長細比、空心率、截面尺寸、偏心距等因素對其力學性能的影響，并提出了極限承載力計算公式.劉濤等[18]、解其鐵等[19]和劉欣榮等[20]采用冷彎薄壁[形鋼拼接成骨架，在其四周粘貼竹膠板形成箱形截面的鋼-竹組合柱，已經完成了對組合柱短期荷載作用下、長期荷載作用下力學性能等方面的研究，分析了試件的破壞形態、破壞特征、承載力、延性等力學性能，并提出了承載力建議公式.

但上述研究均是基于軸心受壓作用下，對偏壓作用下的研究極少.而在實際工程中，由于制作、安裝等原因，柱通常處于偏心受壓的狀態.因此，在已有鋼-竹組合柱研究的基礎上開展偏心受壓力學性能的研究具有非常重要的實際意義.本文以偏心距、長細比、有無螺釘加固為主要參數，對36根鋼-竹組合箱形柱進行偏心受壓試驗，分析了不同參數下組合柱破壞形態、側向撓度及承載力情況，并根據纖維模型法編制了非線性程序，對組合柱進行理論分析計算.

1 試驗概況

1.1 試件設計

本試驗共對36根鋼-竹組合箱形柱進行偏心受壓試驗，根據偏心距、長細比以及是否打螺釘分成15組.為了減小試驗誤差，制作多個相同的試件，試驗結果取其平均值，圖1為部分制作完成的試件.試件截面尺寸均為140mm×140mm，高度h取700、1000、1340、1600mm 4種.組合柱制作所采用的竹膠板厚度均為15mm，冷彎薄壁[形鋼厚度均為2mm.制作試件時先在薄壁[形鋼腹板外側粘貼竹膠板，再將2塊薄壁[形鋼口對口拼接并在兩側翼緣外粘貼竹膠板，形成箱形截面柱.截面組合形式如圖2所示，具體試驗參數列于表1.

圖1 鋼-竹組合箱形柱部分試件Fig.1 Steel-bamboo combination box column

圖2 組合柱截面形式Fig.2 Section form of combination column

表1 試件基本參數

參照GB/T 1927—1943—2009《木材物理力學性質試驗方法》測得竹膠板的抗拉、抗壓強度分別為29.2、23.91MPa，抗拉、抗壓彈性模量分別為8120、7310MPa.依據GB/T 228.1—2010《金屬材料 拉伸試驗 第一部分：室溫試驗方法》測得冷彎薄壁[形鋼的屈服強度為298MPa，抗拉強度為402MPa，彈性模量為2.04×105MPa.

1.2 加載裝置及方案

參照GB/T 50329—2012《木結構試驗方法標準》，在100t反力架上進行試驗(見圖3)，采用力控制和位移控制相結合的分級加載方式，在荷載達到80%極限荷載前采用力控制方式，每級增量為10kN，而后改為位移控制方式，每級荷載持荷60s.軸心受壓試驗在電液伺服萬能試驗機上進行，采用力控制分級加載方式，加載速率為0.5kN/s，直到試件破壞結束.

圖3 加載裝置示意圖Fig.3 Scheme of loading apparatus

沿組合柱高度方向在每個四分點處各設置1個位移計用于測量組合柱側向撓度；為測量試件截面應變，在竹板與薄壁型鋼上粘貼若干應變片，沿組合柱高度方向共設置3層，如圖4所示.通過DH3816型靜態應變采集儀采集試件應變及位移計讀數.

圖4 應變片布置示意圖Fig.4 Distribution of strain gauges

2 試驗結果及分析

2.1 試驗現象及破壞特征

從整個試驗過程和破壞現象來看，可以將試件分為3大類：軸壓試件、考慮偏心距試件、考慮長細比試件，相對應的則有3種破壞形態.

軸心受壓構件的破壞形態均表現為承壓端局部破壞.無螺釘加固試件XZ-P-1在端部出現竹膠板劈裂后向中間延伸，隨后引起鋼-竹界面局部脫膠現象；有螺釘加固試件XZ-L-1因受到螺釘的約束作用，在竹膠板出現劈裂后向中部延伸幅度較小，最終因局部破壞而失去承載能力.軸壓試件具體破壞形態如圖5(a)、(b)所示.

試件XZ-P-2～XZ-P-5和XZ-L-2～XZ-L-5是偏心距不同的偏壓構件，其破壞形態主要是由于試件受壓或受壓較大側牛腿區域出現竹膠板劈裂、鋼材局部向內鼓起等導致的最終破壞.在偏心距較小時(<45mm)破壞相對較為嚴重，且受拉區端部出現界面脫膠(見圖5(c)、(d)).與無螺釘加固試件相比，布設的螺釘在竹膠板產生初始劈裂后能有效約束其劈裂的延續(圖5(e)、(f))，除個別試件外，有螺釘加固試件的極限承載力均有小幅提高.隨著偏心距增大，竹膠板出現劈裂聲的時間不斷提前，例如與偏心距為15mm的試件XZ-P-2相比，偏心距為60mm 的試件XZ-P-5出現劈裂聲時的荷載小了近20%.竹膠板出現劈裂聲后，其表面出現微小裂縫，荷載增加速度略有下降；加載到80%極限荷載時，劈裂聲密集且清晰；隨著荷載增長，試件受壓或受壓較大側牛腿區域竹膠板裂縫擴大明顯，對應位置腹板處竹膠板向外鼓起，鋼-竹界面出現脫膠現象，試件因無法繼續承受荷載而停止加載.試件XZ-P-6和XZ-L-6由于偏心距過大，加載過程中受鉸支座的影響，在未出現明顯破壞的情況下因出現較大轉動而終止加載.

長細比較大且偏心距相同試件XZ-C-2、XZ-C-3的破壞形態主要為受壓側中部翼緣竹膠板劈裂，腹板處竹膠板向外鼓起，內部鋼板出現局部屈曲凸起(見圖5(g)、(h)).在加載到60%極限荷載時，試件開始出現細微的竹膠板劈裂聲，但外部無明顯現象；達到90%極限荷載時，竹膠板劈裂聲清晰且密集，并且受壓側竹膠板出現斷裂現象，側向撓度明顯；接近極限荷載時，竹膠板劈裂嚴重，側向撓度驟增，表現出一定的脆性破壞特征.試件XZ-C-1由于長細比增幅較小，仍是牛腿區域出現破壞.

圖5 鋼-竹組合柱破壞形態Fig.5 Failure modes of steel-bamboo composite column

2.2 影響因素分析

2.2.1偏心距

不同偏心距條件下試件的荷載-柱中部側向撓度(N-um)曲線、極限承載力Nu與偏心距關系曲線如圖6、7所示.由圖6可見，各試件N-um曲線在初期均呈線性增長；隨后由于竹膠板劈裂、鋼材局部屈曲使曲線斜率逐漸減小，側向撓度增長速率加快，曲線呈非線性增長.由圖7可見，偏心距對試件極限承載力影響較大，隨著偏心距增大，試件極限承載力明顯降低.從試件XZ-P-1到XZ-P-5，試件極限承載力下降幅度依次為26.04%、23.10%、23.07%、9.52%.在偏心距較小時，其變化對試件極限承載力影響較大，之后隨著偏心距增大，試件極限承載力變化減緩.試件XZ-P-6因提前終止加載，其承載力與側向撓度并未達到極限值.

圖6 試件荷載-側向撓度曲線Fig.6 Load-lateral deflection curves

圖7 試件極限承載力-偏心距曲線Fig.7 Ultimate load-eccentricity curves of specimens

2.2.2長細比

本試驗共設計了4種長細比的試件(XZ-P-4、XZ-C-1～XZ-C-3)，其N-um曲線如圖8所示.隨著長細比的增大，試件可視為中柱，本身存在一定的初始撓曲，考慮到偏心距與長細比的耦合效應，此時承載力和側向撓度受偏壓及初始撓曲的共同影響.長細比最大試件XZ-C-3的極限承載力下降較為顯著，其余試件的極限承載力隨長細比增加呈下降趨勢，側向撓度的增長則明顯加快.可見在設計參數范圍內，長細比改變對試件極限承載力有一定影響且是非線性遞減.

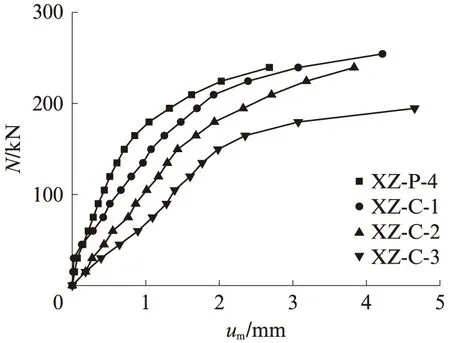
圖8 試件XZ-P-4、XZ-C-1～XZ-C-3的荷載-側向撓度曲線Fig.8 Load-lateral deflection curves of specimens XZ-P-4 and XZ-C-1-XZ-C-3

2.2.3有無螺釘加固

無螺釘加固試件XZ-P-1～XZ-P-6和有螺釘加固試件XZ-L-1～XZ-L-6的屈服承載力和極限承載力見表2.由表2可知，除了提前破壞的試件XZ-L-6和軸壓試件XZ-L-1外，其余有螺釘加固試件的屈服承載力和極限承載力均高于無螺釘加固試件，說明螺釘的加固連接對試件承載力起到了提高作用且影響較為明顯.試件XZ-L-1的屈服承載力有一定提高，但后期由于螺釘約束了竹膠板劈裂的發展，局部出現應力集中，使其比無螺釘的試件更早達到破壞.對比試件XZ-P-4、XZ-L-4的N-um曲線(見圖9)可見，初期2條曲線發展趨勢較為相近，有螺釘加固試件的側向撓度略微偏大些許，但隨著荷載增加，撓度增長逐漸變緩.螺釘的加固連接使鋼板與竹材能更好地協同工作，有效減緩了試件側向撓度的增長速率，降低了試件最終撓度.

表2 螺釘加固對試件承載力影響

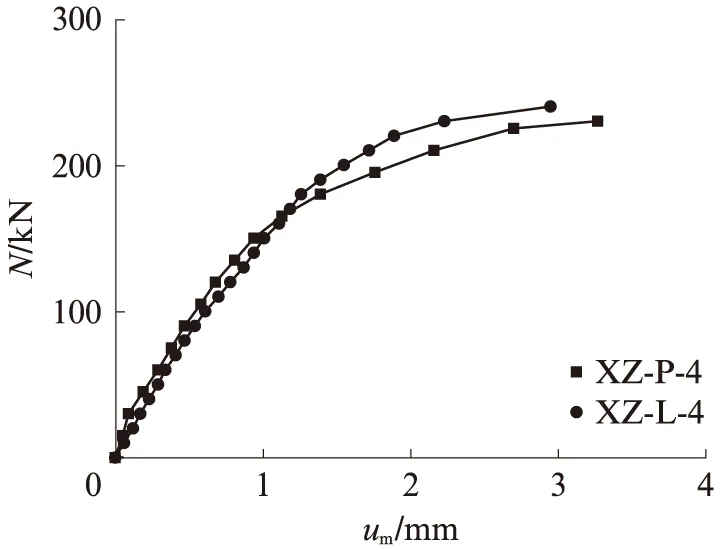
圖9 試件XZ-P-4、XZ-L-4荷載-側向撓度曲線Fig.9 Load-lateral deflection curves of specimens XZ-P-4 and XZ-L-4

2.3 荷載-縱向應變關系

分析整個受壓過程柱中截面應變變化可知，在偏心距小于30mm時表現為全截面受壓，隨著偏心距增大，過渡為一側受拉一側受壓狀態.

圖10 薄壁型鋼和竹膠板荷載-縱向應變關系曲線Fig.10 Load-strain curves of thin-walled steel and bamboo plywood

部分典型試件受拉側和受壓側薄壁型鋼、竹膠板的縱向應變ε隨荷載N變化的關系曲線如圖10所示，其中應變受拉為正，受壓為負.由圖10可見：在加載初期，薄壁型鋼和竹膠板的荷載-應變曲線均呈線性增長，曲線發展趨勢幾乎一致，兩者應變較為接近，具有較好的協同性；當荷載達到70%～90%的極限荷載時，翼緣薄壁型鋼先屈服；后隨著2種材料均進入屈服階段，鋼-竹界面出現部分脫膠現象，2種材料的應變不再同步，但發展趨勢仍基本一致.整個加載過程中，隨著荷載增加，薄壁型鋼、竹膠板受壓或受壓較大側應變增加幅度總大于另一側；而受拉或受壓較小側應變在荷載達到極限承載力前發展都比較緩慢.在試驗設計參數范圍內，除個別試件外，大多數試件的受拉纖維(或較小受壓纖維)在極限承載力前均未出現明顯破壞現象.

2.4 柱中截面應變及側向撓度曲線

圖11為典型試件XZ-P-4和XZ-P-5柱中截面應變沿高度方向分布曲線.由圖11可見：在各級荷載作用下，2種試件柱中截面應變沿高度分布基本為直線，中性層位置保持不變且偏向于受拉一側；隨著荷載增大，組合柱受彎后截面仍保持平面，符合平截面假定.對比(a)、(b)2圖可見，中性軸位置隨著偏心距的增大逐漸向受壓側移動.

圖11 柱中截面平均應變沿截面高度分布Fig.11 Distribution of longitudinal strain in the column

圖12 試件XZ-P-4的整體變形曲線Fig.12 Overall deformation curve of specimen XZ-P-4

組合柱在不同的受力階段，其側向撓度的變化具有一定的規律性，以典型試件XZ-P-4為例，其整體變形曲線如圖12所示.由圖12可見：在各級荷載作用下，試件側向撓度的分布沿柱高基本對稱，且變形曲線近似為正弦半波曲線；加載初期，組合柱整體性能良好，鋼竹共同工作，試件處于彈性階段，側向撓度變化幅度較小且呈線性增大；隨著加載至60%極限荷載左右時，組合柱進入塑性階段，鋼竹之間出現細微脫膠，側向撓度增加加大.

3 理論分析

3.1 纖維模型法

采用纖維模型法將截面劃分成若干條帶，假設每一條帶上應力均勻分布且應變保持一致[21-22].本文根據截面形狀和實際尺寸，在平行于中和軸方向，將上下翼緣處竹膠板劃分為5個條帶(高度為3mm)、薄壁型鋼劃分為1個條帶(高度2mm)，腹板處均劃分為53個條帶(高度2mm).截面單元劃分及應變如圖13所示，圖中ΔAbi、ΔAsi分別為竹膠板、薄壁型鋼任一條帶單元的面積，mm2.竹膠板應力-應變關系參考文獻[23]及改進的Saenz公式，采用式(1)所示的單軸作用下竹材本構關系；薄壁型鋼考慮其屈服強化，采用式(2)表示的彈塑性本構模型.

(1)

(2)

式中：Eb為竹材抗拉彈性模量，MPa；Es為鋼材彈性模量，MPa；fy為鋼材屈服強度，MPa；fyu為鋼材極限強度，MPa；εy=fy/Es；εh=10εy；εsu=100εh.

圖13 截面單元劃分示意圖Fig.13 Schematic diagram of section unit division

3.1.1基本假定

應變分析結果表明，組合柱受彎變形后截面仍基本保持平面，應變沿截面高度呈線性分布，鋼、竹2種材料之間具有較好協同性，變形發展基本一致.由前文分析可得，試件的側向撓度曲線沿柱高對稱分布且形狀近似為正弦半波曲線.基于上述分析，此處作如下幾個基本假定：

(1)截面應變分布符合平截面假定.

(2)薄壁型鋼與竹膠板之間無相對滑移.

(3)構件兩端為鉸接，側向撓度曲線為正弦半波曲線.

(4)不考慮薄壁型鋼局部屈曲的影響.

(5)只考慮縱向平衡和變形協調條件.

(6)薄壁型鋼的抗拉強度與抗壓強度相等，抗拉彈性模量與抗壓彈性模量相等，即fs=f′s，Es=E′s.

3.1.2計算過程

(1)定義組合柱中部側向撓度為um，可得曲率公式：

φ=π2um/L2

(3)

(2)假定截面形心處應變為ε0，根據平截面假定，利用式(4)可得截面上任一條帶單元形心處的應變εi，其中yi為任一單元形心到截面形心的距離.

εi=ε0+φyi

(4)

(3)根據材料的本構關系得出任一單元形心處薄壁型鋼和竹膠板的應力σsi、σbi.

(4)根據力的平衡條件，可得軸力Nin、彎矩Min的迭代方程：

(5)

(6)

式中：n為竹膠板劃分的條帶單元數量；m為薄壁型鋼劃分的條帶單元數量.

(5)根據式(5)、(6)分級增加變形Δum，不斷調整ε0來滿足條件要求，迭代求得內力Nin、Min.當內力Nin與外力N相等時，認為滿足平衡條件.參考文獻[24]，可提出適用于纖維模型法的收斂依據：

(7)

N=Min/(e0+um)

(8)

式中：δ為收斂容差，取0.005；e0為初始偏心距，mm.

當內外力滿足收斂依據，且承載力下降到80%極限承載力后停止計算.具體計算流程如圖14所示.

圖14 計算流程圖Fig.14 Calculation flow chart

3.2 計算結果與試驗結果對比

根據前文所述，編制了基于纖維模型法的組合柱偏心受壓非線性計算程序，對不同偏心距、長細比的組合柱進行全過程分析計算，并將計算所得的荷載-撓度曲線與試驗所得曲線進行對比，兩者對比結果如圖15所示.由圖15可見，各個試件的計算結果與試驗結果吻合較好，該計算方法可以較好地預測組合柱的變形和承載力.試件XZ-P-6因偏心距最大，加載過程中受到鉸支座的影響，出現了較大轉動幅度而失穩，導致加載提前終止，故不再對其進行分析.對于偏心距、長細比較小的試件，該計算方法效果尤為突出，如試件XZ-P-2～XZ-P-4和XZ-C-1的計算曲線與試驗曲線幾乎重合，其他試件略有偏差但并不明顯.

由程序求得的承載力計算值Nuc和試驗所得值Nue如表3所示.在計算有螺釘加固試件的承載力時，用影響系數γ來表示螺釘對組合柱承載力的影響.由前文分析中可知，螺釘的布設對組合柱承載力有一定的提高，故本試驗γ取1.05.由表3可得，計算值與試驗值吻合良好，誤差均在10%以內，平均誤差僅為4.51%.

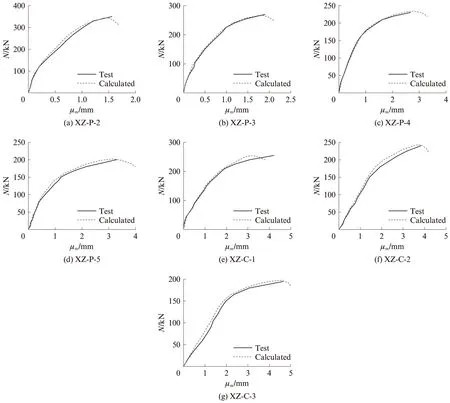
圖15 計算曲線與試驗曲線對比Fig.15 Comparison of calculated curves and test curves

表3 試驗結果與計算結果對比

4 結論

(1)鋼-竹組合箱形柱的破壞形態主要可分為3類：軸壓試件為承壓端材料破壞；長細比較小的不同偏心距試件均為受壓或受壓較大側牛腿區域竹膠板劈裂和鋼材向內凸起；長細比較大的試件為受壓側中部竹膠板劈裂且向外鼓起，內部鋼板局部屈曲.

(2)偏心距對組合柱力學性能影響較大.隨著偏心距的增大，組合柱承載力呈下降趨勢，側向撓度呈增大趨勢.偏心距較小時，組合柱承載力下降較明顯；偏心距較大時，組合柱承載力下降幅度相對減緩.長細比對組合柱極限承載力有一定影響但無較明顯的規律性.螺釘的加固連接使組合柱屈服承載力和極限承載力均得到了一定的提高，且影響較為明顯.

(3)組合柱受拉和受壓側型鋼、竹材的荷載-縱向應變曲線發展趨勢基本一致，2種材料協同受力.組合柱中截面應變近似呈線性分布，符合平截面假定；中性軸偏向于受拉一側，且隨著偏心距的增大向受壓側移動.各級荷載下組合柱側向撓度的分布沿柱高基本對稱，近似為正弦半波曲線.

(4)基于纖維模型法編制的非線性計算程序適用于鋼-竹組合箱形柱，程序計算所得的N-um全過程曲線與試驗曲線吻合良好，能較好地預測構件的變形和承載力.由程序求得的承載力理論計算值與試驗值基本吻合，誤差均在10%以內，平均誤差僅為4.51%.