基于TIR 透鏡的LED 光源準直輸出探究

秦 晉，秦會斌，邱定忠，葉 晨

（杭州電子科技大學 電子信息學院，浙江 杭州 310018）

0 引言

隨著社會的高速發展，LED 作為一種新型光源也在快速發展，目前已經成為了一項具有發展前景的技術產品。 與其他光源相比，LED 具有高亮度、壽命長、功耗低、價格低廉、節能環保等諸多優勢，被廣泛應用在路燈、照明、醫學及顯示等領域[1～4]。 對于一般的LED 光源，出射光分布遵從朗伯型分布，其發散角約為120°，發散角大，如果直接應用，光能利用率低，且很難滿足一些照明場合需要達到的性能指標，如均勻度、亮度等[5]。為了解決上述問題，需要給LED 光源進行二次光學設計， 那就是給LED 配光來控制光線輸出方向，減小發散角，提高光能利用率。

基于非成像光學理論的系統光學設計已經成為了當下人們研究的熱點，相關設計方法也在逐漸完善。 常用的設計方法主要分兩大類：一類是針對點光源的設計，如裁剪法、偏微分方程法、數值分析法等；另一類是針對面光源的設計，如同步多曲面設計法[6～9]。

本文根據邊緣光線原理及同步多曲面設計法設計了一種基于全內反射（TIR）透鏡的準直系統，通過TIR 透鏡控制光線輸出方向， 對光線進行準直，提高光能利用率。 然后利用光學軟件Tracepro對光線進行追跡仿真，根據追跡結果來反饋并優化設計，最終達到最優準直效果。

1 TIR 透鏡的設計

TIR 透鏡的設計目的在于控制光線輸出方向，減小光束的發散角，達到準直效果，實現均勻、高亮度的照明，同時提高光能的利用率。

TIR 透鏡的工作原理圖如圖1 所示。由于LED具有旋轉對稱性， 透鏡曲面可由AB段、BC段、CD段、DE段、EF段和FA段構成的橫切面繞對稱軸EF旋轉360°構成。 LED 光源位于中心點O點，大角度的光線由AB旋轉面全反射成為平行光，再經過FA旋轉面射出； 小角度的光線由DE旋轉面折射成為平行光，再經過FA旋轉面射出，從而達到準直的效果。 在設計中，BC段為直線段，不起光學作用，長度為0.2mm，進行固定；CD段可以稍微傾斜，便于模具制造。

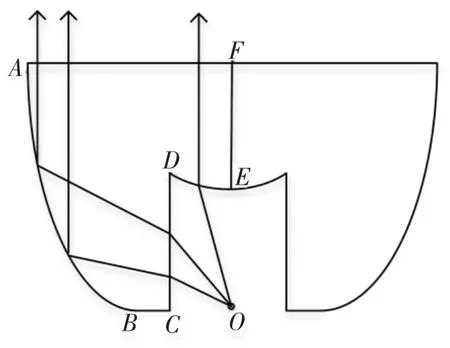
圖1 TIR 透鏡的工作原理圖Figure 1 Working principle diagram of TIR lens

1.1 內折射面的設計

內折射面的設計示意如圖2 所示，LED 光源位于O點。P1點為內折射面的最低點，該點位于LED光源的正上方的主軸上， 設其對應坐標為（0，y1，0），N1為P1點的法向矢量，N1的方向垂直向上。然后根據第一個點推算出第二個點的坐標。 以N1為法線矢量，過P1點作切平面，該平面為與水平面平行的平面， 它與入射角為θ1的光線相交于點P2（x2，y2，0）。 設入射角為θ1的光線的方向矢量為I，其歸一化的坐標為（cos（θ1），sin（θ1），0），由于TIR透鏡起到準直效果， 所以光線會垂直向上出射，設出射矢量為O（0，1，0）。 將光線入射矢量I 及出射矢量O 代入到斯涅耳（Snell）定律中（式1），就可以求出P2點的方向矢量N2。 其中n為光入射介質折射率與出射介質折射率的比值， 因為介質為空氣，折射率可看成是1，所以n就是TIR 透鏡光學材料折射率的倒數[10]。

圖2 內折射面的設計示意圖Figure 2 Schematic diagram of the design of the internal refractive surface

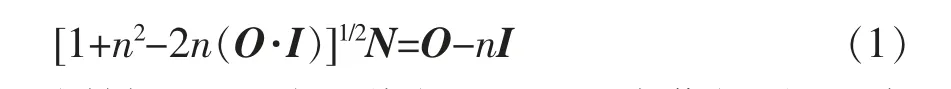
同樣，以N2為法線矢量，過P2點作切平面，該平面與入射角為θ2的光線相交于P3（x3，y3，0），再將入射角為θ2的光線的入射光線和出射光線的方向矢量歸一化坐標I2（cos θ2，sin θ2，0）和O2（0，1，0）代入到Snell 定理（式1）中即可求得P3點的法向矢量N3。

通過采用這種方法可以由第i個點Pi點的坐標（xi，yi，0）、法向矢量Ni、入射矢量歸一化坐標Ii（cos θi，sin θi，0）及出射矢量歸一化坐標Oi（0，1，0）求出曲線下一個點Pi+1的坐標（xi+1，yi+1，0），從而求出內折射面的輪廓曲線。

1.2 側面全反射面的設計

側面全反射面的設計如圖3 所示，LED 光源位于O 點。 P1點為側面全反射面的最低點，該點位于光源水平橫軸上，設其坐標為（x1，0，0），N1為P1點的法向矢量， 其方向與主軸成45°夾角，P1點的橫坐標減去不起光學作用的固定長度0.2mm 即為全反射面的內半徑R0， 然后根據第一個點推算第二個點的坐標。假設已知第二條光線與水平軸之間的夾角為θ1，以N1為法線矢量，過P1點作切平面，該平面與水平面成45°夾角，它與入射角為θ1的光線相交于P2點，其坐標為（x2，y2，0）。設入射角為θ1的入射光線的方向矢量為I， 其歸一化的坐標為（cos θ1，sin θ1，0），由于TIR 透鏡的準直作用，所以出射光線會豎直向上，設出射光線矢量歸一化坐標為O（0，1，0）。 將入射矢量I及出射矢量O代入到Snell定律（公式2）中，就可以求出P2點的方向矢量N2。其中n 為透鏡光學材料折射率的倒數。

圖3 側面全反射面的設計示意圖Figure 3 Schematic diagram of the design of the lateral total reflection surface

在求出P2點法向矢量后， 同樣以P2點的法向矢量N2為法線矢量，過P2點作切平面，其平面與入射角為θ2的光線相交于P3（x3，y3，0），再根據入射角為θ2的光線的入射矢量I2（cos θ2，sin θ2，0）和出射矢量O2（0，1，0）以及Snell 定律求出P3點的法向矢量N3。

通過采用這種方法可以通過由第i 個點Pi的坐標（xi，yi，0）、法向矢量歸一化坐標Ni、入射矢量歸 一 化 坐 標Ii（cos θi，sin θi，0） 及 出 射 矢 量Oi（0，1，0）求出曲線下一個點Pi+1的坐標（xi+1，yi+1，0），從而求出全反射面的輪廓曲線。

通過上述設計方法得到兩條由一系列離散點組成的輪廓曲線，將這些離散點導入到SolidWorks中并采用坐標點放樣生成曲線的方法進行擬合生成實體輪廓曲線，然后將實體輪廓曲線繞主軸旋轉360°即可得到TIR 透鏡的三維模型。

2 模擬仿真

根據上述設計所得的TIR 透鏡三維模型如圖4 所示。

圖4 TIR 透鏡的三維示意圖Figure 4 Three-dimensional schematic diagram of TIR lens

將該實體模型導入光學軟件Tracepro 中進行模擬仿真，TIR 透鏡的光學材料采用PMMA， 其折射率為1.4935， 設置LED 光源為點光源后進行光線追跡， 其光線追跡如圖5 所示。 從圖可以看出，LED 光源發出的大角度的光線及小角度的光線通過TIR 透鏡都能準直輸出。

圖5 點光源下的光線追跡圖Figure 5 Ray tracing diagram under point light source

設置LED 光源為檔案光源， 檔案光源采用CREE 公司的XLamp XPE 光源。 設置好接收面后對LED 光源的出射光線進行光線追跡， 其光線追跡如圖6 所示。

圖6 檔案光源下的光線追跡圖Figure 6 The ray tracing diagram under the file light source

從圖中可以看出，LED 光源發出的光線經TIR透鏡配光后，光束基本達到準直效果。

圖7 和圖8 分別為接收面上的照度分布圖和發光角度分布圖。由圖可以看出TIR 透鏡的光能利用率為90.33%，接收面上光斑均勻，光束的發散角較小，大致集中在±8°以內。

圖7 照度分布圖Figure 7 Illumination distribution map

圖8 發光角度分布圖Figure 8 Luminous angle distribution diagram

3 結語

本文根據邊緣光線原理及SMS 法設計了一種基于TIR 透鏡的準直系統，通過該系統控制光線輸出方向、準直光線，并通過Tracepro 對設計的實體模型進行仿真模擬。 其光能利用率為90.33%，光束發散角在±8°左右。仿真結果表明，在該結構相對簡單的準直系統下，光能利用率高，且有效地對LED光源的輸出光線進行了準直。