美國早期代數教科書中的“負負得正”解釋方式研究

邵愛娣，栗小妮，汪曉勤

美國早期代數教科書中的“負負得正”解釋方式研究

邵愛娣，栗小妮，汪曉勤

（華東師范大學 教師教育學院，上海 200062）

選取1820—1939年間出版的200種美國早期代數教科書，研究發現：書中“負負得正”的解釋方式共有7類，即利用分配律、連減法、利用相反數、歸納法、幾何方法、物理模型和生活模型．1880年以前，教科書中多采用利用分配律和連減法；1880年后，多種方法并存，利用分配律解釋呈逐漸下降趨勢，物理模型和生活模型占比逐漸上升，相反數法和連減法占比普遍較高．了解“負負得正”的多種解釋方式和歷史演變，有助于教科書編寫者和教師深刻理解符號法則的合理性，選擇易于學生理解的解釋方式．

代數教科書；負負得正；解釋；生活模型

1 問題提出

“負負得正”是初等代數中的一個十分重要的符號法則，早在公元7世紀就已為印度數學家婆羅摩笈多（Brahmagupta）所知．13世紀，意大利數學家斐波那契（L. Fibonacci）在《計算之書》中提出“負負得正”法則，但只將其用于計算(-)(-)，而非兩個純粹的負數相乘．之后，中國數學家朱世杰在《算學啟蒙》中也提出“正負術”：“同名相乘為正，異名相乘為負．”16~17世紀，歐洲數學家，如德國的斯蒂菲爾（M. Stifel）和克拉維斯（C. Clavius）等相繼在其代數著作中提出符號法則．到了18世紀，英國數學家桑德森（N. Saunderson）、瑞士數學家歐拉（L. Euler）等先后試圖對符號法則進行“證明”．19世紀，德國數學家漢克爾（H. Hankel）和F·克萊因（F. Klein）揭示了“負負得正”無法證明的事實．

18世紀以來，“負負得正”法則始終是數學教學中的一個難點．19世紀法國著名作家司湯達（Stendhal）因為他的兩位數學老師未能合理解釋“負負得正”的緣由而對數學失去了興趣[1]．著名昆蟲學家法布爾（H. Fabre）在自學數學時因教科書未能清晰地解釋“負負得正”而“吃盡苦頭”．[2]即使是到了今天，很多學生對于該法則也仍只知其然而不知其所以然．鞏子坤的調查顯示，97%的學生能夠利用“負負得正”法則進行運算，但不超過11.5%的學生可以給出合理的解釋，說明對于學生來說，運用法則容易，但理解卻很困難[3]．因此，選擇恰當的方法去解釋符號法則，乃是教科書編寫者和數學教師需要解決的重要問題．

賈隨軍等的研究表明，20世紀以來中學數學教科書對于“負負得正”的解釋主要有“運用現實模型”“運用相反數的性質”“隱性運用分配律”“顯性運用分配律”“運用減法運算”“運用變換”等6種方式[4]．但上述研究僅局限于國內外34種中學數學教科書，其中國外教科書10種，國內教科書24種．還需要以更寬闊的視野去研究“負負得正”的歷史，以便為今日教科書編寫、課堂教學以及HPM課例研究提供更豐富的素材和更深刻的思想．為此，對1820—1939年間出版的美國代數教科書進行考查，試圖回答以下問題：美國早期代數教科書如何解釋“負負得正”？從中可以總結出哪些類型？“負負得正”的解釋方式在120年間經歷了怎樣的嬗變過程？對今日教科書編寫和課堂教學有何啟示？

2 研究對象

從HathiTrust數字圖書館中搜索19~20世紀的美國代數教科書全文，對于不同時間出版的同一作者的教科書，若書名和內容一致，則視為同一種教科書，選取最早的一個版本；若書名不同，則視為不同的兩種教科書．最終，在1820—1939年間出版的代數教科書中選出200種，若以20年為一段，則200種代數教科書的分布情況如圖1所示．

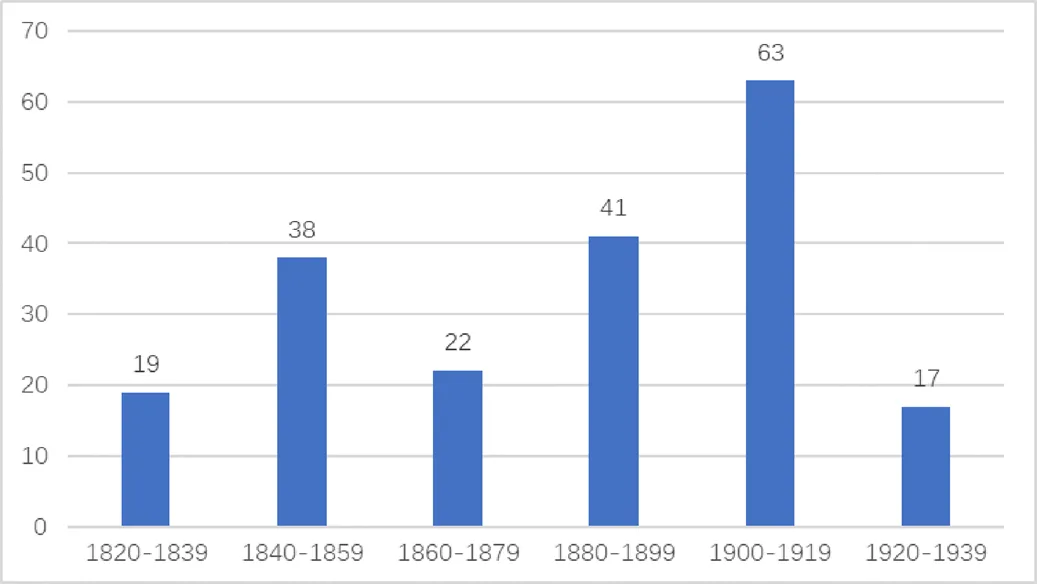
圖1 200種教科書的時間分布

200種教科書的書名互有不同，有《代數基礎》《代數專著》《代數初階》《代數導引》《代數舉要》《初等代數》《學校代數》《中學代數》《大學代數》《大中學代數》，等等．

200種代數教科書中，174種是中學教科書，19種是大學教科書，7種高中和大學合本．“負負得正”法則出現在“乘法”“正數和負數”“負數”“乘法和除法”等章節，出現在“乘法”章節的最多，占63.5%，其次是“正數和負數”，占14%．

所有200種教科書都對“負負得正”法則做出了各自的解釋，研究者對這些解釋進行仔細地歸類和分析．對于不易歸類或有歧義的解釋方式，研究者一起交流研討，最終確定其所屬類別．

3 關于“負負得正”的解釋

200種教科書中，關于“負負得正”的解釋方式可以分為利用分配律、連減法、利用相反數、歸納法、幾何方法、物理模型和生活模型7類．200種教科書中，175種各給出了1類解釋，24種各給出了兩類解釋，只有1種教科書給出了3類解釋．7類解釋共出現226次，具體分布情況如圖2所示．

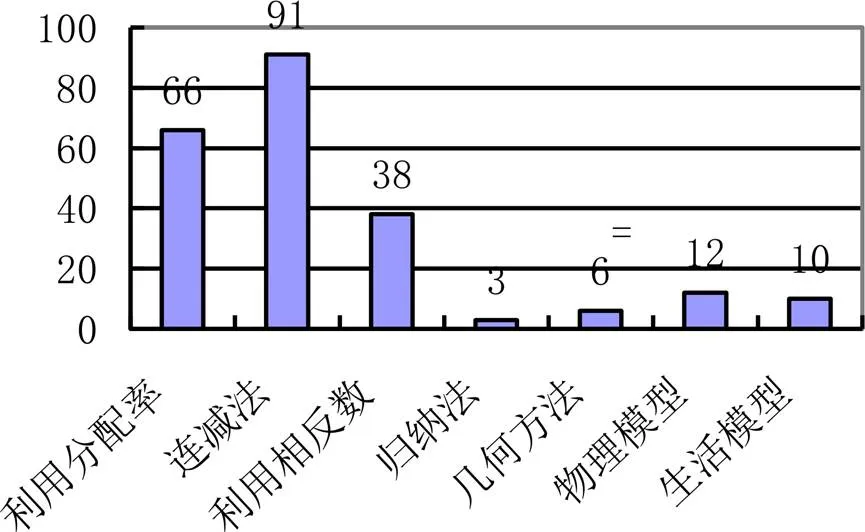
圖2 “負負得正”解釋方式的分布

3.1 利用分配律

共有66種教科書（占29.2%）運用（或逆向運用）乘法分配律，試圖去證明“負負得正”，F?克萊因稱之為“半邏輯證明”．具體有以下4種做法．

方法1 利用(-)(-)．

這種方法源于斐波那契．在《計算之書》中，斐波那契利用幾何方法證明了等式

(-)(-)=--+(>>0,>>0) （1）

如圖3所示[5]．有55種教科書直接利用公式（1）得出“負負得正”，但只有Schuyler通過擴大（1）的適用范圍給出進一步的解釋：若在（1）中，設==0，則(+)×(+)=+；若==0，則(-)×(+)=-；若==0，則(+)×(-)=-；若==0，則(-)×(-)=+[6]．

方法2 利用(-)(-)或(-)×[(-)+]．

有8種教科書采用此法．如Hill先“證明”正負得負：因(-)×[+()]×=()×0，故(-)×=-．再由(-)(-)=[+(-)](-)=(-)+(-)(-)=-+(-)(-)=0，得到(-)(-)=[7]．

Slaught & Lennes和Rietz首先“證明”正負得負：設×(-)=，則×(-)+=+，即×[(-)+]=+，于是得0=0=+，故=-，即(-)=-．再設(-×(-)=，則(-)×(-)+(-)×，即(-)×[(-)+]=-，于是得(-)×0=0=-，故(-)×(-)=[8，9]．

方法3 利用(-)×[-(+)]．

有兩種教科書采用此法．將-視為-(+)，則有(-)×(-)=(-)×[-(+)]=--[-(+)]=--(--)=-++=[10]．

方法4 利用[(+)-(+)](-)．

只有一種教科書采用此法．考慮[(+)-(+)](-)，一方面，利用“正負得負”，有[(+)-(+)](-)=(+)(-)-(+)(-)=--(-)=-+(+)．另一方面，[(+)+(-)](-)=-+(-)(-)，故得(-)×(-)=+[11]．

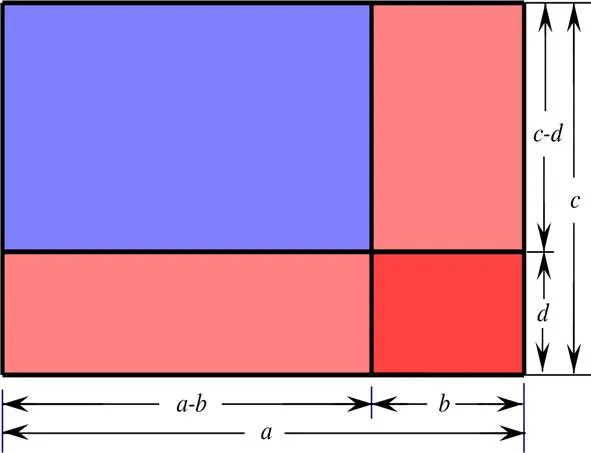
圖3 斐波那契的幾何證明

3.2 連減法

“連減法”是對乘法意義的拓廣：將一個數乘以一個正整數，相當于連加該數若干次；將一個數乘以一個負整數，相當于連減該數若干次，由此得到“負負得正”．共有91種教科書（占40.3%）采用此法．例如：

(+4)×(+3)=+(+4)+(+4)+(+4)=+12；

(-4)×(+3)=+(-4)+(-4)+(-4)=-12；

(+4)×(-3)=-(+4)-(+4)-(+4)=-12；

(-4)×(-3)=-(-4)-(-4)-(-4)=+12[12]．

3.3 利用相反數

所謂相反數法，是將(-)×和(-)×(-)看作一對相反數，若已知前者為負，則后者必為正．這種方法源于歐拉．歐拉在《代數基礎》中首先通過債務的倍數來說明正負得負：將-視為債務，取三次，則債務必變成三倍多，故(-)×3=-3(>0)，一般地，有(-)×=-(>0,>0)，故“正負得負”．由于(-)×(-) (>0,>0)要么等于，要么等于-，但已證(-)×=-，故(-)×(-)=[13]．共有38種教科書（占16.8%）采用此法．具體有以下3種方式．

方法1 反證法．

有3種教科書采用反證法．如Young的解釋是：若承認(-)×=-（已證），則必有(-)×(-)=+，否則(-)×=(-)×(-)，于是=-，矛盾[14]．

方法2 直接改變符號．

共有32種教科書采用此法．如Smyth的解釋如下：若乘數為+，則被乘數保留自己的符號，重復次，于是有(+)×(+)=+，(-)×(+)=-；若乘數為-，則被乘數取相反符號，重復次，于是有(+)×(-)=-，(-)×(-)=[15]．后來的作者多傾向于用具體數字來說明這種情形，先說明(-3)×4=-12，而(-3)×(-4)意指-3改變符號，即為3再重復4次，即(-3)×(-4)=12[16]．

方法3 利用-1的意義．

這種方法的出發點是“-1與任意一個數的乘積等于該數的相反數”或“乘以-1就是取一次、變符號”．有3種教科書采用此法．如：

(-)×(-)=(-1)××(-)=(-1)×(-)×=[17]；

(-3)×(-4)=(-1)×3×(-4)=(-1)×(-12)=+12[18]；

(-)×(-)=×(-1)××(-1)=×(-1)×(-1)=(-)×(-1)=[19]．

3.4 歸納法

這種方法最早為桑德森所采用．桑德森在《代數基礎》中先提出命題：“一個等差數列的各項依次乘以同一個數，所得乘積構成等差數列．”利用該命題，等差數列4，0，-4依次乘以3，所得乘積構成等差數列，前兩個乘積依次為12和0，故第3個乘積為-12，即(-4)×3=-12；依次乘以-3，所得乘積構成等差數列，前兩個乘積依次為-12和0，故第3個乘積為12，即(-4)×(-3)=12[20]．有3種教科書采用此法．

Benedict取等差數列+4，+3，+2，+1，0，-1，-2，-3，-4，先將各項分別乘以+3，觀察所得等差數列的規律，得出“負正得負”；再將數列各項分別乘以-3，觀察新數列的規律，得出“負負得正”，如圖4[21]．

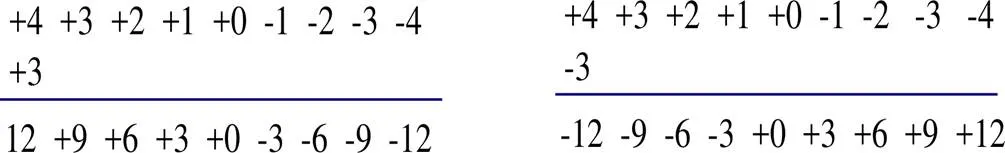
圖4 Benedict“負負得正”的解釋方式

3.5 幾何方法

有6種教科書采用有向線段來解釋“負負得正”．如Newcomb給出如下幾何解釋：假設表示從零點向右長度為1 cm的線段，則-表示從零點向左長度為1 cm的線段，如圖5[22]．

圖5 Newcomb“負負得正”的幾何解釋

Long & Brenke設向右為正方向，用3個單位長度在直線上沿著正方向測量5次，所測得的線段長度為(+5)×(+3)=+15．若沿著反方向測量5次，得(-5)×(+3)=-15．用反方向的3個單位長度沿著該方向測量5次，得(+5)×(-3)=-15．將反方向上3個單位長度反向測量5次，得(-5)×(-3)=+15，如圖6[23]．

3.6 物理模型

部分教科書利用物理量之間的關系，如浮力、行程、杠桿等解釋“負負得正”，將其歸類為利用“物理模型”解釋．

3.6.1 氣球模型

利用氣球所受浮力大小來說明正負數的乘法法則，稱為“氣球模型”，有5種教科書采用此法．如Slaught & Lennes的解釋如下：一位氣球駕駛員在出發之前，做了如下準備工作：（1）他給氣球充入9000立方英尺的氣體，氣體每一千立方英尺的上升力為75磅．（2）他取了8袋沙子，每袋重15磅．則此時氣球受到的浮力為(+75)×(+9)=+675磅，受到的阻力為120磅，即(-15)×(+8)=-120磅．若在氣球飛行過程中，駕駛員打開閥門，放掉2000立方英尺的氣體，相當于氣球受到的阻力增加了150磅，即(+75)×(-2)=-150磅；若駕駛員扔掉4袋沙子，相當于氣球受到的浮力增加了60磅，即(-15)×(-4)=+60磅[24]．

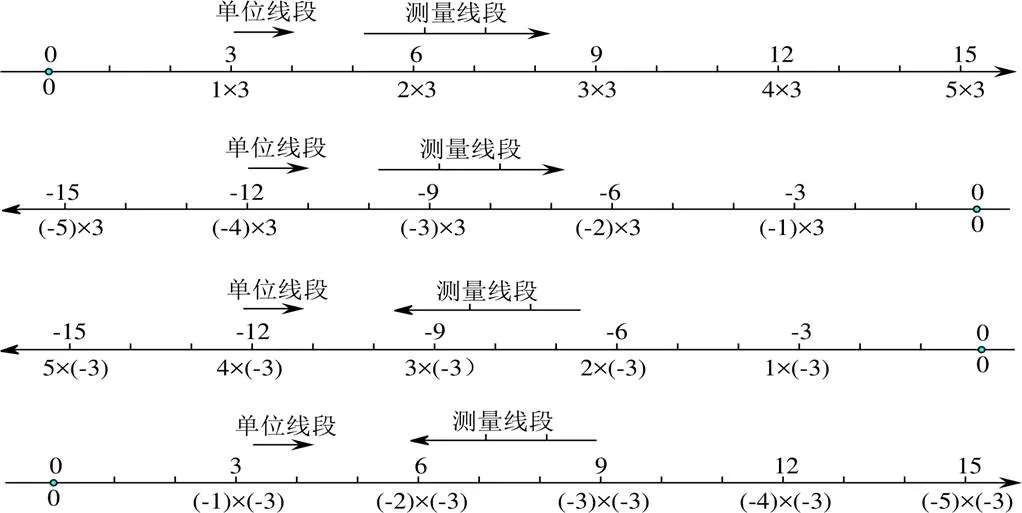
圖6 Long &Brenke“負負得正”的幾何解釋

3.6.2 行程模型

利用物體行駛過程中路程、速度和時間的關系解釋“負負得正”稱為“行程模型”，有5種教科書采用此法．如Oliver, Jones & Wait中給出了以下解釋：一列火車以20英里/小時的速度從西往東開，現經過A處，則5小時后，將到達A處以東100英里處，此即20×(+5)=+100；5小時前，位于A處以西100英里處，此即20×(-5)=-100．若火車以20英里/小時的速度從東往西開，現經過A處，則5小時后，將到達A處以西100英里處，此即(-20)×(+5)=-100；5小時前，位于A處以東100英里處，此即(-20)×(-5)=100[25]．

Hopkins則采用人的運動來解釋，如圖7．規定向東走為正，向西走為負，未來的時間為正，過去的時間為負．一個人以每小時3英里的速度向東走，4個小時后他位于起點東面12英里處，即(+4)×(+3)=+12．一個人以每小時3英里的速度向西走，4小時后他位于起點西面12英里處，即(+4)×(-3)=-12．一個人以每小時3英里的速度往東走，4小時前他位于起點西面12英里處，即(-4)×(+3)=-12．一個人以每小時3英里的速度向西走，4小時前他位于起點東面12英里處，即(-4)×(-3)=+12[26]．

圖7 Hopkins“負負得正”行程模型圖示

3.6.3 力矩模型

Keal & Leonard采用了力矩模型，如圖8．規定支點右邊的臂為正，支點左邊的臂為負，向上的作用力為正，向下的作用力為負，逆時針方向轉動的力矩為正，順時針方向轉動的力矩為負．正力作用于正力臂，杠桿沿逆時針方向旋轉，產生正力矩，即(+3)×(+7)=21；負力作用于正力臂，杠桿沿順時針方向旋轉，從而產生負力矩，即(+3)×(-7)=-21；正力作用于負力臂，杠桿沿順時針方向轉動，產生負力矩，即(-3)×(+7)=-21；負力作用于負力臂，杠桿沿逆時針方向旋轉，即(-3)×(-7)=21[27]．

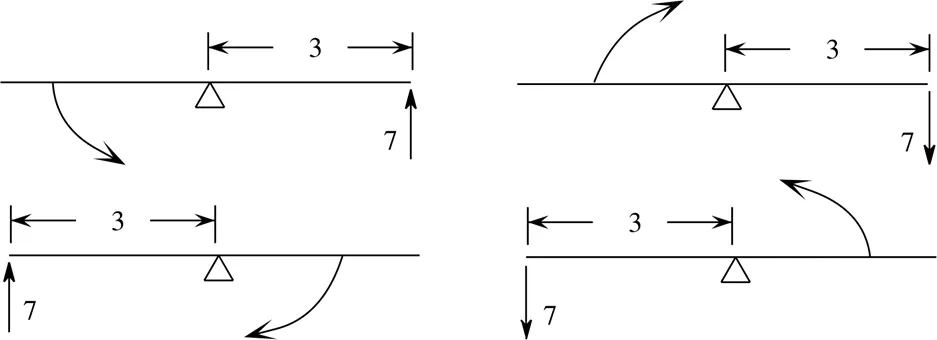
圖8 Keal & Leonard“負負得正”的力矩模型圖示

3.6.4 水箱模型

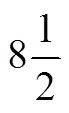
3.7 生活模型

“生活模型”是指基于現實生活情境（如收入、債務等）的解釋方式，具體可分成以下兩種情形．

有5種教科書采用節約和浪費[29]、收益和損失[30]來解釋“負負得正”．如Beman和Smith設計了如下情境：某鎮上每人每周需納稅1美元，若有5人遷入該鎮，則該鎮每周增加收入(+5)×(+1)=+5美元；若有5人遷出該鎮，則該鎮每周增加收入(-5)×(+1)=-5美元．該鎮每周為每個流浪漢支付1美元，若有5個流浪漢遷入，則該鎮每周增加收入(+5)×(-1)=-5美元；若有5個流浪漢遷出，則該鎮每周增加收入(-5)×(-1)=+5美元[31]．

美國數學家和數學史家M·克萊因（M. Kline）最早用債務解釋“負負得正”．假定某人每天欠債5美元（記為-5），在給定日期他身無分文（0美元）．那么在給定日期3天后（記為+3）他欠債15美元，即(+3)×(-5)=-15；在給定日期3天前（記為-3），他的財產比給定日期多15美元，即(-3)×(-5)=15[32]．

有5種教科書采用了該模型，如Durell & Robbins給出如下解釋：（1）100美元取5次，得500美元，即(+100)×(+5)=+500；（2）100美元的債務取5次，得-500美元，即(-100)×(+5)=-500；（3）100美元扣除5次，得-500美元，即(+100)×(-5)=-500；（4）100美元的債務扣除5次，相當于增加了500美元，即(-100)×(-5)=+500[33]．

4 分布與討論

4.1 各種解釋方式的分布

由于每個時間段選擇書的數量不均，研究采用百分率統計．以20年為一段，這7類解釋的分布如圖9所示．

從圖9可見，1880年以前，“負負得正”的解釋方式較為單一，以利用分配律和連減法解釋為主，其中利用分配律解釋占主導地位，但隨著時間的推移，該方法所占的比率逐漸下降．1880年后，解釋方式逐漸多樣化，出現了幾何方法、物理模型和生活模型等．

圖9 諸解釋方法的分布變化

1840年后，利用分配律逐漸減少，連減法逐漸增加．在研究限定的時間范圍內，連減法占比僅次于利用分配律．該方法僅拓展了乘法的意義，再結合加減法的性質，受到早期教科書編寫者的青睞．

相反數法在所有解釋方式中位列第三．1820—1859年之間該解釋方式共出現6次，每個時間段占比較為接近．1860—1879年之間沒有出現，在該時間段，大部分作者傾向于連減法．1880—1939年之間共出現32次，相比于1820—1859年，每個時間段的占比逐漸上升．可見，相反數法由于簡潔明了而成為19世紀后期和20世紀初期教科書編寫者偏愛的方法之一．

歸納法出現于1840年后．在200種教科書中，歸納法共出現3次，在所有方法中出現次數最少．國內現行人教版和北師大版教科書也采用了這種方式．

幾何方法主要借助于有向線段的度量來解釋符號法則，出現于19世紀后期，但次數較少．該方法雖然直觀，但由于蘊含向量思想，且正向和反向測量與有向線段的正負方向易于混淆，對學生來說未必容易，這大概是教科書編寫者很少選擇它的原因．

物理模型和生活模型出現于1880年后，與前5種解釋方式相比，兩類模型將數學與現實情境聯系起來，由生產、生活中的實際事例抽象出符號法則，較之幾何方法更直觀，更易于接受，故隨著時間的推移，占比逐漸上升．國內現行部分教科書也選擇了物理模型，如滬教版采用行程模型，蘇科版采用水位升降模型．

4.2 討論

利用分配律、相反數法、連減法、歸納法和幾何法都是從數學內部出發解釋符號法則，而物理模型和生活模型則從數學外部出發來解釋該法則．盡管物理模型和生活模型呈逐漸上升的趨勢，但大部分教科書（占總數的90.7%）依然局限于數學內部的邏輯關系．

“負負得正”解釋方式的演變與數學和數學教育的進步息息相關．就數學而言，1880年以前的教科書毫無例外都試圖從數學內部出發“證明”負負得正．但隨著時間的推移，數學家逐漸認識到“負負得正”不能證明的事實．19世紀德國數學家漢克爾發現，“在形式化的算術中，負負得正是不能證明的．”F·克萊因將負負得正法則視為“危險的絆腳石”，他對數學教師提出忠告：“不要試圖去證明符號法則的邏輯必要性，別把不可能的證明講得似乎成立．”[34]自此人們才發現，教科書中利用分配律所進行的“證明”，其實根本不是真正的證明．因此，1880年以后，用分配律來“證明”負負得正的教科書顯著減少．

物理模型和生活模型的出現和占比的逐漸上升與19世紀末20世紀初的數學教育變革有關．1892年，美國組織了全國性的中等學校教學委員會，重新制定中等學校教育目標和標準課程計劃，倡導算術要具體化，努力把算術、代數和幾何互相聯系起來[35]．20世紀初出現了國際性的數學教育改革運動．1901年，培利（J. Perry）認為數學教學的目的不是為了考試和創造數學家，實用性決定了應該教什么．新的教學方法應該讓人們認識到數學的實用性．他主張教學要基于學生的經驗，讓學生自己構建抽象的概念．1902年，受培利的影響，美國數學會會長穆爾（E. H. Moore）呼吁要少強調數學的系統性和形式化，多強調數學的實用性，提倡實驗的教學方法[36]．在這些背景下，更多的教科書作者開始關注“負負得正”法則與現實情境之間的聯系，生活模型或物理模型應運而生．

5 結論與啟示

綜上，1820—1939年間的200種美國早期代數教科書采用了多種不同的方式解釋“負負得正”．從早期的3種方式發展到后期的7類方式并存．隨著時間的推移，“半邏輯”的分配律方法解釋逐漸減少，連減法逐漸占據上風，成為數學家們喜愛的方式．在此期間，歸納法僅僅曇花一現．19世紀末20世紀初開始，受數學教育改革的影響，幾何方法、物理模型和生活模型逐漸進入人們的視野，并且其占比逐漸上升．盡管如此，連減法和相反數法仍然占據優勢．

早期教科書中的“負負得正”解釋方式及其演變規律，為今日的教科書編寫、教師專業發展和課堂教學帶來一定的啟示．

5.1 對教科書編寫的啟示

早期教科書中“負負得正”法則的解釋為今日教科書編寫提供了豐富的材料．教科書編寫者可以考慮如何展示“負負得正”這一法則的產生和形成過程，才能讓學生感受到它的合理性．賈隨軍等在其考查的各版教科書中發現，約6成教科書從數學本身解釋“負負得正”法則[4]．早期教科書編寫者也更傾向于從數學內部出發解釋“負負得正”，如連減法和相反數法．盡管物理模型和生活模型更具趣味性，但其中涉及幾個變量的實際意義，不易為學生所理解；而連減法和相反數法言簡意賅，較易理解．今日教科書編寫者可以兼顧兩種方式，讓學生明白：不論從數學內部出發還是從現實情境出發，“負負得正”都是合理的存在．

5.2 對教學的啟示

早期教科書中“負負得正”解釋方式的研究，可以讓教師了解一個看似簡單的法則背后的歷史軌跡，知道“負負得正”是為了保證已有運算律成立而作出的“規定”，教師不要試圖在教學中證明法則的合理性，因而犯科學性錯誤．同時，早期教科書中的7類解釋方式為教師提供了豐富的教學資源和更多的選擇；從不同解釋方式出現的頻數，也可以看到前人的傾向性，為自己的選擇提供參考．另外，通過了解歷史上數學家認識“負負得正”的曲折過程以及“負負得正”解釋方式的演變，教師可以預測學生的認知障礙，自信而坦然地面對學生“為什么負負得正”的疑問，保護學生的好奇心和求知欲，滲透數學德育，實現人性化的數學教育．

有理數乘法教學的難點在于如何向學生解釋“負負得正”的合理性．教學在運用早期教科書所提供的有關素材時，既可以采用復制式，也可以采用順應式．例如，學生在學習有理數乘法時已經學習了有理數的減法和相反數等知識，這時選用連減法和相反數法較為合適．對于物理模型和生活模型，教師可選擇學生熟悉的情境，并進行適當改編，作為數學解釋的補充．

[1] 佟巍，汪曉勤．負數的歷史與“負負得正”的引入[J]．中學數學教學參考，2005（Z1）：126-128．

[2] 法布爾．昆蟲記（卷九）[M]．魯京明，梁守鏘，譯．廣州：花城出版社，2001：126-127．

[3] 鞏子坤．“負負得正”何以能被接受[J]．數學教學，2010（3）：7-10．

[4] 賈隨軍，劉明君，葉蓓蓓，等．20世紀以來中學數學教材中“負負得正”法則解釋方式的研究[J]．數學教育學報，2015，24（4）：76-81．

[5] Siegler L E. Fibonacci’s liber abaci: A translation into modern English of Leonardo Pisano’s book of calculation [M]. New York: Springer-Verlag, 2002: 510-511.

[6] Schuyler A. A complete algebra for schools and colleges [M]. Cincinnati: W. Hinkle, 1870: 24-27.

[7] Hill D H. Elements of algebra [M]. Philadelphia: J. B. Lippincott, 1859: 24-29.

[8] Slaught H E, LENNES N J. High school algebra: Advanced course [M]. Boston: Allyn and Bacon, 1908: 9.

[9] Rietz H L. College algebra [M]. New York: H. Holt and Co., 1910: 8.

[10] ?Strong T. A treatise on elementary and higher algebra [M]. New York: Pratt, Oakley & Co., 1859: 20-21.

[11] ?Lefevre A. Number and its algebra [M]. Boston: D.C. Heath & Co., 1896: 90.

[12] ?Taylor J M. A college algebra [M]. Boston: Allyn & Bacon, 1889: 12.

[13] ?Euler L, FARRAR J. An introduction to the elements of algebra [M]. Cambridge: Hilliard and Metcalf, 1821: 9-11.

[14] ?Young J R. An elementary treatise on algebra [M]. Philadelphia: Carey, Lea & Blanchard, 1838: 21-22.

[15] ?Smyth W. Elementary algebra [M]. Portland: O. L. Sanborn and Co., 1850: 60-62.

[16] ?Hall H S, KNIGHT S R. Elementary algebra for schools [M]. London: Macmillan & Co, 1885: 26-27.

[17] ?Keigwin H W. Principles of elementary algebra [M]. Boston: Ginn & Co., 1886: 9-10.

[18] ?Taylor J M. A college algebra [M]. Boston: Allyn & Bacon, 1889: 13-14.

[19] ?Hayes E. Algebra for high schools and colleges [M]. Norwood: J. S. Cushing & Company, 1897: 20-21.

[20] ?Saunderson N. The elements of algebra [M]. Cambridge: The University Press, 1739: 56-58

[21] ?Benedict J T. Elements of algebra [M]. New York, 1877: 15-16.

[22] ?Newcomb S. A school algebra [M]. New York: H. Holt, 1882: 90-91.

[23] ?Long E. BRENKE W C. Algebra [M]. New York: The Century Co., 1913: 71-73.

[24] ?Slaught H E, LENNES N J. High school algebra: Complete Course [M]. Boston: Allyn and Bacon, 1908: 62-63.

[25] ?Oliver J E, JONES G W, WAIT L A. A treatise on algebra [M]. Ithaca: The Authors, 1882: 11-12.

[26] ?HopkinsJ W. A first book of algebra [M]. New York: The Macmillan Co., 1905: 49-50.

[27] ?Keal H M, LEONARD C J. Mathematics for electrical students [M]. New York: J. Wiley & Sons, 1938: 40-42.

[28] ?Aley R J, ROTHROCK D A. The essentials of algebra [M]. New York: Silver, Burdett, 1904: 40-41.

[29] ?Rushmer C E, DENCE C J. High school algebra [M]. New York: American Book Company, 1923: 73-74.

[30] ?Engelhardt F, HAERTTER L D. First course in algebra [M]. Philadelphia: The John C. Winston Company, 1926: 75-76.

[31] ?Beman W W, SMITH D E. Elements of algebra [M]. Boston: Ginn, 1900: 40-41.

[32] ?Boulet G. On the essence of multiplication [J]. For the Learning of Mathematics, 1998, 18 (3):12-18.

[33] ?Durell F, ROBBINS E R. A school algebra complete [M]. New York: Maynard, Merrill & Co., 1897: 39.

[34] ?Klein F. Elementary mathematics from an advanced viewpoint [M]. New York: Dover Publications, 1945: 23-28.

[35] 馬忠林．數學教育史[M]．南寧：廣西教育出版社，2001：339-355．

[36] ?Hassler J O, HEDRICK E R, SMITH R R. The teaching of secondary mathematics [M]. New York: The Macmillan Company, 1935: 105-130.

An Examination of the Methods Performing the Multiplication with Two Negative Numbers in Early Algebra Textbooks in the USA

SHAO Ai-di, LI Xiao-ni, WANG Xiao-qin

(College of Teacher Education, East China Normal University, Shanghai 200062, China)

About 200 algebra textbooks, published between 1820 and 1939 in the USA, were selected to analyze their explanation of the Multiplication of two Negative numbers. It was found that there were seven types of interpretation methods in the books: distribution law, repeated subtraction, opposite number, induction, geometric method, physical model, and life model. Before 1880, many textbooks adopted the distributive law and repeated subtraction. After 1880, a variety of methods coexisted, and interpretation using the distributive law showed a gradually declining trend. The proportion using the physical model and life model methods increased gradually, and the proportion using the opposite number method and repeated subtraction method were generally higher. It is helpful for textbook writers and teachers to have a deep understanding of the rationality of the sign rules and choose the interpretation method that is easiest for students to understand.

algebra textbook; the multiplication with two negative numbers; explanation; life model

G633.62

A

1004–9894（2021）01–0085–06

邵愛娣，栗小妮，汪曉勤．美國早期代數教科書中的“負負得正”解釋方式研究[J]．數學教育學報，2021，30（1）：85-90．

2020–09–30

上海高校“立德樹人”人文社會科學重點研究基地之數學教育教學研究基地研究項目——數學課程與教學中落實立德樹人根本任務的研究（A8）

邵愛娣（1990—），女，江蘇鹽城人，碩士生，主要從事數學史與數學教育研究．

[責任編校：陳雋、張楠]