函數與不等式齊驅并駕 多角度解決最值問題
——2020年全國Ⅱ卷第21題一題多解探討
張培杰 韓 業
(云南省大理大學教師教育學院 671000)
韓業(1996.6-),男,大學,從事數學教學研究.
一、真題再現
(2020年全國Ⅱ卷第21題)已知函數f(x)=sin2xsin2x.
(1)討論f(x)在(0,π)的單調性;
通過觀察題目發現,該題以三角函數為背景,考查判斷函數在區間內的單調性、求函數值域、不等式證明等多個知識點. 題目綜合性強,難度較大,對考生的邏輯推理能力和運算能力有較高的要求,很好的體現了課程標準要求的核心素養導向,具有高考命題需要的區分度. 下面重點給出第(2)問的一題多解,對于第(1)、(3)問僅給出一種可行的解答.
二、真題解析
(1)分析要討論函數f(x)在區間內的單調性,只需要求導,由導函數值在區間內的正(負)可得到原函數在區間內單調遞增(減),該題是常規考法.
解答對函數f(x)=sin2xsin2x求導,得f′(x)=2sinxcosxsin2x+2sin2xcos2x=2sin2x(2cos2x+1),



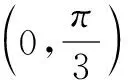
分析1 直接求導,利用函數單調性求最值. 要想求出函數的最值(取值范圍),借助導數先判斷單調性再求最值是最常用的方法. 因此,可以借助導數解答這個問題.


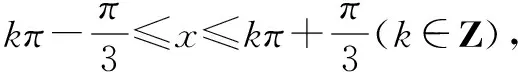


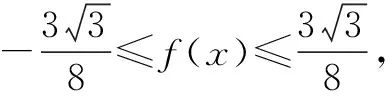
評析這種解法是能夠容易想到的,觀察解答過程可以發現,對計算的要求較高. 此外,需要考生對三角函數的圖象性質非常熟悉才能由f′(x)≥0(或f′(x)≤0)正確的求出x的范圍. 體現了數學運算核心素養,考查學生的綜合運用能力.
分析2 利用三角函數周期性,轉化為連續函數在區間上的最值問題. 周期性是三角函數的一個重要性質,該題以三角函數為背景,易想到利用周期性解決. 由三角函數周期性,可以把問題轉化為求一個閉區間內的最值問題,只要求出函數在這個區間內的最值即可.
解答2由題意,f(x+π)=sin2(x+π)sin2(x+π)=f(x),所以π是f(x)的一個周期.因此,問題可以轉化為:

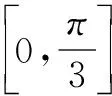

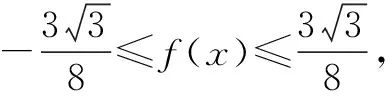
評析這種解法較為靈活,要求學生具有抽象概括的能力、直觀想象的核心素養,能夠在看到三角函數時候即想到周期性,并將問題轉為為一個閉區間上的最值問題. 學生在平時復習中,要熟練掌握基礎知識,還要注意抽象概括能力的培養.
分析3平方處理,利用四元均值不等式證明.題目要證的式子中含有絕對值,可以通過平方去掉絕對值. 平方后,問題轉化為求乘積的最大值,可以構造四元均值不等式.
解答3 由題意,
[f(x)]2=sin4x·sin22x
=4sin6x·cos2x


分析4 先降冪化次數為1,再平方處理,利用四元均值不等式證明. 題目所給函數表達式兩個因式的次數不統一,可以利用降冪公式把兩項次數都化為1. 此時,再通過平方去掉絕對值,問題再次轉為為求乘積的最大值,可以構造四元均值不等式.
解答4 由題,



評析這兩種解法都蘊含兩個關鍵思路,一是看到絕對值想到通過平方取絕對值,二是能夠想到均值不等式中“和定積最大”解決最值問題. 不同的是,解法3直接平方處理,解法4先降冪再處理.不論哪一種解法,都要求對三角函數相關公式非常熟悉,有較強的運算能力才能正確解答. 此外,教材中所學的是二元均值不等式,這兩種解法都用到四元均值不等式,要求學生具有較強的邏輯推理能力.



將x依次替換為2x,22x,23x,…,2n-1x,

累乘,得
sin4x·sin6(2x)·sin6(22x)·sin6(23x)
·…·sin6(2n-1x)·sin2(2nx)
又因為sin6x·sin6(2x)·sin6(22x)
·…·sin6(2n-1x)·sin6(2nx)
=(sin2x·sin4(2nx))·sin4x·sin6(2x)·sin6(22x)
·…·sin6(2n-1x)·sin2(2nx)
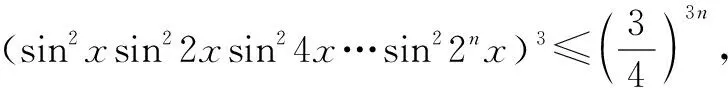

評析該題涉及到三角函數性質,絕對值處理,數列累乘,放縮證明不等式等知識點和相關方法,綜合性強,難度較大,很好體現了高考的選拔性功能. 在平時復習中,首先應注重夯實基礎,其次要注意多個知識點的融合,培養學生的綜合運用能力.
可以發現,高考數學壓軸題融合的知識點較多,綜合性強,難度大,是最容易體現高考區分度的題型. 基于對今年高考題的分析解答,提出如下復習建議:
1.重視基礎知識學習,強化基本技能訓練
基礎知識是“四基”能力培養和核心素養養成的最重要載體,概念的形成過程就是數學抽象和數學建模的過程.因此,要深刻理解相關知識的基本概念,理解公式定理的形成過程,掌握基本方法的適用“題境”,加強審讀問題、分析問題、解決問題的訓練.
2. 關注數學思想方法的應用,培養數學核心素養
在平時教學和學習中,引導學生正確使用數學思想放方法分析問題,訓練他們抽象概括、轉化問題的能力,提高數學運算能力,從多個方面培養數學核心素養.
3. 研究高考命題思路,總結命題規律
高考試題是命題專家根據《課程標準》和考試大綱精心打造的,復習通過研讀近些年的高考試題,分析理解命題思路、意圖和理念,總結命題規律. 通過研讀高考題,避免大搞題海戰術,實現高效備考.

