優化學習路徑 培養科學思維
——淺談復合場中“有效最低點”的幾種求法
嚴 霓
(江蘇省常州市金壇區第一中學 213200)
物理核心素養是學生在接受物理教育過程中逐步形成的適應個人終身發展和社會發展需要的必備品格和關鍵能力,是學生通過物理學習而內化的帶有物理學科特性的品質,是學生科學素養的關鍵成分,科學思維是從物理學視角對客觀事物的本質屬性、內在規律及相互關系的認識方式;是基于經驗事實建構物理模型的抽象概括過程;是分析綜合、推理論證等方法在科學領域的具體運用;是基于事實證據和科學推理對不同觀點和結論提出質疑和批判,進行檢驗和修正,進而提出創造性見解的能力與品格.主要包括四個內容:模型建構、科學推理、科學論證、質疑創新.
教師在平時教學中,注重優化學習路徑,讓學生經歷具體的學習過程,培養科學思維,復合場中的“有效最低點”問題是高考的重點,也是難點,而曲線運動中一種特殊的運動——圓周運動,也是常考的一種形式,復合場豎直平面內的圓周運動,是圓周運動的常見模式,而豎直平面內的圓周運動的有效“最低點”是解決這一類問題的關鍵點,對于“有效最低點”的位置的求法,很多同學把握不住,不知道怎么求,基于這個情況,本人總結了幾個有效最低點的幾種解法.
例題如圖1所示,水平方向的勻強電場中,有一質量為m的帶電小球,用長為L的細線懸于O點,當小球平衡時,細線和水平方向的夾角為θ,現給小球一個初速度.速度方向和細線垂直,使小球恰能在豎直平面內做圓周運動,則圓周運動過程中速度的最小值為多少?
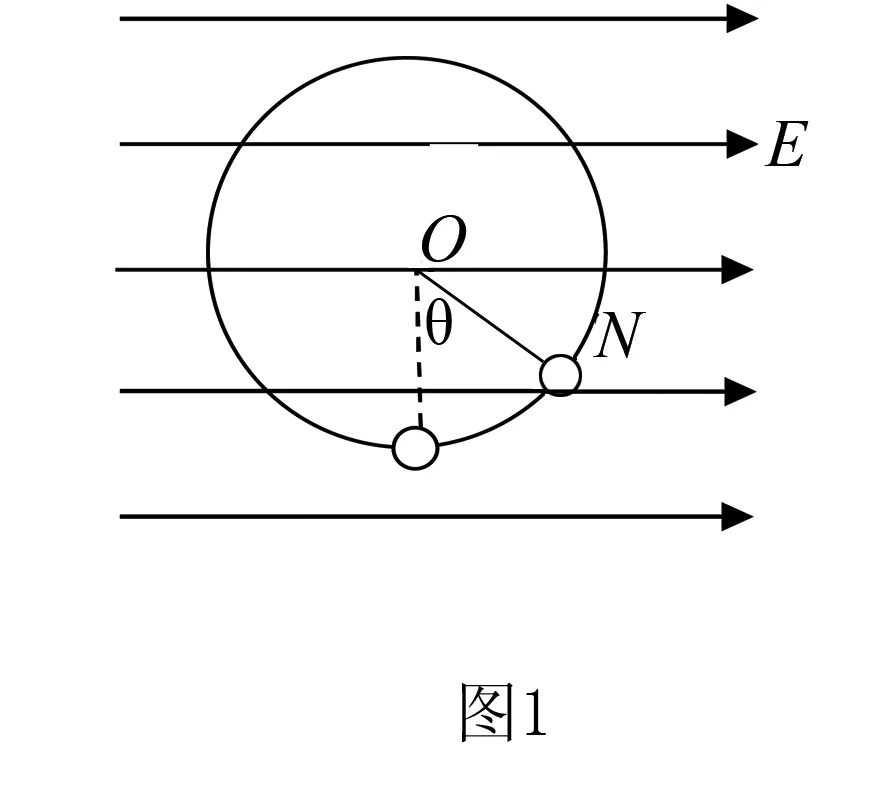
解析此時最高點的速度并不是最小速度,最低點也不是最大速度的位置,它的“等效最低點位置”在哪?又如何求等效最高點的位置?
關于“等效最低點”的位置,本人總結了下,我們可以從以下幾個方面來找“等效最低點”.
解法一等效替代法, 復雜問題簡單化
方法依據既有重力場和勻強電場,但合場也是恒定不變的,與處理重力場類似.所以可以把重力和電場力合成,求出合力,把這個合力等效成“重力”,我們把該合力稱之為“等效重力”,此時相當于只有“重力”作用 ,那么運動過程中沿著等效重力的方向,該點則為等效最低點.(如圖2的M即為“等效最高點”,N點即為“等效最低點”)
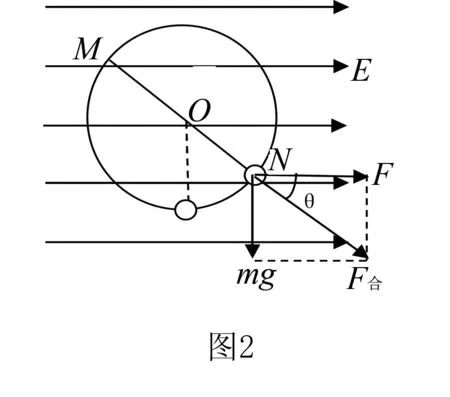
解題策略電場中帶電粒子在豎直平面內做圓周運動:
等效“最高點” :物體速度最小,繩的拉力最小.
特點:mg和Eq的合力與繩的拉力在同一直線上,且方向相同.
等效“最低點”:物體速度最大,繩的拉力最大
特點:mg和Eq的合力與繩的拉力在同一直線上,且方向相反.
所以,速度最小值為“等效最高點”(M點)

解法二動力學法,運動情景清晰化

方法依據如圖3,我們找某一位置進行受力分析,把重力和電場力合成一個力F合,而合力F合產生兩個效果,一個是沿速度方向(切線方向),一個沿半徑方向,沿速度方向,用來改變速度的大小,我們可以發現,當F合有速度方向(切線方向)分量時,速度的大小就改變,而我們的“最低點”的速度最大,所以只有當F合與繩的拉力(半徑方向)在同一直線上,F合就沒有速度方向的分量,這時速度就最大或最小.
解題策略我們從受力分析可以得出,合力F合所在的延長線必須為直徑時,就沒有速度方向(切線方向)分量,該延長線與圓的交點為“最高點”、“最低點”.
所以我們求速度最大值,可以得出

解法三功能關系法,解題目標明確化
方法依據1.功能關系依據:最低點特點:速度最大,動能就最大.
解題策略當物體運動到合外力與位移夾角小于90度時,合外力做正功,動能逐漸增加(如圖4甲); 當物體運動到合外力與位移夾角大于90度時,合外力做負功,動能逐漸減小(如圖4乙),所以當物體運動到合外力與位移夾角等于90度時(即垂直時),此時動能最大,此時合外力的反向延長線正好經過圓心.如圖4丙所示.

解法四數學最值法,物理問題數學化
方法依據1.依據三角函數求最值
2.數學最值法具體解法

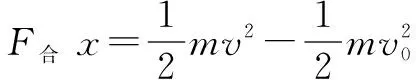

根據“等效最低點”速度最大,可知,動能最大.
即求


即求Y的最大值

所以“等效最低點”和圓心的連線與F合方向平行,速度最大.
得出“等效最低點”的反向延長線經過圓心.
本文對“有效最低點”的找法,做了一點粗略的介紹,希望對讀者有一定的幫助,有不足之處,還望大家批評指正.

