正弦與非正弦激勵下高頻變壓器磁心損耗計算與驗證

劉福貴， 趙 琳， 蔣嘉誠

(1. 省部共建電工裝備可靠性與智能化國家重點實驗室， 河北工業大學， 天津 300130；2. 河北省電磁場與電器可靠性重點實驗室， 河北工業大學， 天津 300130)

1 引言

近年來，隨著電力電子技術的快速發展，電力電子變壓器廣泛應用在電網中。國內外學者為設計出更加高效，更易控制的電力電子變壓器不斷地進行探索[1，2]。隨著電力電子變壓器的持續發展，在其中起到電氣隔離與電壓等級變換的高頻變壓器的應用越來越廣泛。由于工作頻率的提升，高頻變壓器磁心的損耗相應增高，導致磁心內部溫度增高，降低了高頻變壓器的使用壽命以及系統的穩定性，因此研究高頻變壓器的磁心損耗具有重要意義[3-5]。

目前，磁心損耗主要計算方法分為兩類，一類為磁滯模型法，另一類為損耗數學模型法。磁滯模型雖然具有明確的物理含義且精度較高，但模型過于復雜，參數提取困難，耗費時間較長，所以一般在工程實踐中常采用損耗數學模型法來進行計算[6]。文獻[7]將損耗分離模型由三項式變為兩項式，在此基礎上將激勵電壓傅里葉分解成多次諧波疊加形式，引入激勵電壓的平均值與有效值，提取校正系數進而求得磁心損耗。但由于文中將剩余損耗項歸于渦流損耗，影響了損耗計算的準確性。文獻[8]將動態磁滯回線與橢圓磁滯回線進行等效，求得等效磁場強度、磁通密度與頻率之間的關系，進而求得磁心損耗。但文中缺少對方波與三角波電壓激勵下的損耗計算分析。文獻[9]對比分析了三種基于損耗分離理論下的非正弦計算模型，將三種模型在PWM激勵下的計算結果與實驗數據進行比較，發現三種模型在磁通密度大于1 T的情況下三種模型計算結果精確。但在磁通密度較小時，計算誤差較大。

為解決上述所存在的問題，實現高頻變壓器磁心損耗的準確計算，本文基于Bertotti損耗分離模型，引入了渦流損耗與剩余損耗修正系數，推導出在方波和三角波激勵下損耗分離計算模型，實現了在非正弦激勵下高頻變壓器磁心損耗的計算。并根據損耗系數變化特征，將損耗系數改進，提高了正弦激勵下模型的計算精度。在此基礎上代入修正系數，對非正弦激勵下損耗分離模型進一步改進，并將測量值與計算結果進行比較，驗證了文中所提模型的有效性。

2 非正弦激勵下損耗分離模型

意大利學者Bertotti解析了鐵磁材料損耗產生的不同機理，將鐵磁材料的損耗分為三部分：磁滯損耗Ph、渦流損耗Pe、剩余損耗Pex[10]。

2.1 經典正弦損耗分離模型

根據Bertotti損耗分離理論，損耗模型的計算公式如式(1)所示：

(1)

式中，f為激勵電壓頻率，Hz；Bm為磁通密度峰值，T；σ為材料電導率；ρ為材料密度；d為材料疊片厚度,mm；T為磁化周期,s；G為無量綱系數(G=0.137 5)；S為疊片橫截面積，mm2；V0為鐵磁材料內部統計參數。

在正弦電壓激勵條件下，磁通密度表達式為B(t)=Bmcos(ωt)，代入式(1)可得正弦激勵下損耗計算公式為：

(2)

式中，Kh為磁滯損耗系數；Ke為渦流損耗系數；Kex為剩余損耗系數。

2.2 確定正弦損耗分離模型參數

為了得到正弦電壓激勵下Bertotti損耗分離模型損耗系數，本文首先采用環形測量法測量非晶與納米晶磁心損耗數據。在正弦激勵下,測量頻率范圍為1～10 kHz(每1 kHz遞增)，測量非晶磁環磁通密度范圍為0.1～1.3 T(每0.1 T遞增)，測量納米晶材料磁通密度范圍為0.1～1.2 T(每0.1 T遞增)，得到正弦激勵下非晶和納米晶材料不同工況下損耗數據如表1和表2所示。

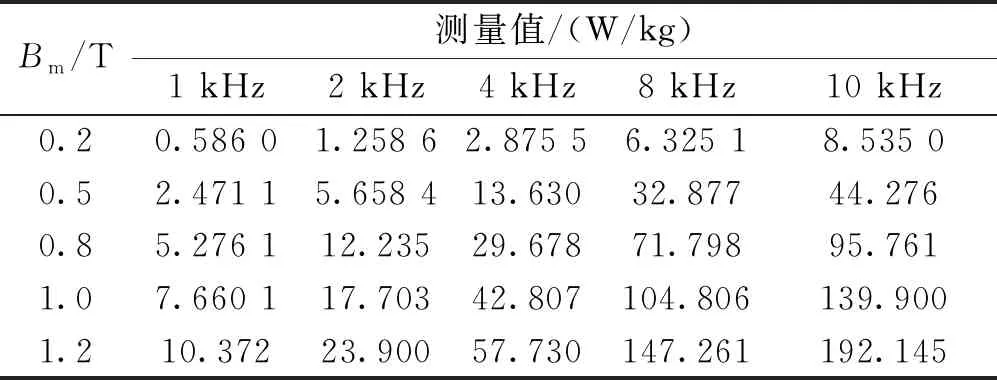
表1 非晶正弦激勵下損耗數據

然后，依照測量得到的損耗數據，采用最小二乘法對式(2)進行損耗參數擬合，得到正弦電壓激勵下非晶與納米晶磁心損耗計算公式為：

(3)

(4)

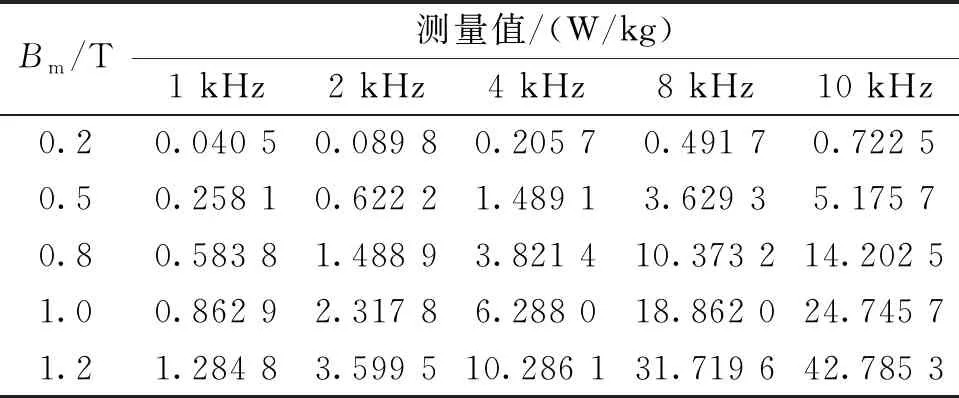
表2 納米晶正弦激勵下損耗數據

2.3 修正損耗分離模型

在實際應用中，高頻變壓器常工作于方波與三角波等非正弦電壓的激勵下，因此，式(2)不能滿足計算精度的要求。參照損耗分離理論中各個損耗產生的機理，在磁感應強度與頻率相同的情況下，磁滯損耗一般不發生變化。所以，在不同電壓波形的激勵下，磁心損耗的差異主要由于渦流以及剩余損耗發生變化。因此，為得到方波和三角波電壓激勵下磁心損耗分離計算模型，本文引入渦流與剩余損耗修正系數，對經典正弦損耗分離模型進行修正[11，12]。

2.3.1 方波激勵下損耗分離模型

方波激勵時電壓與磁通密度在一個周期內隨時間變化波形如圖1所示，公式如式(5)和式(6)所示。

圖1 方波電壓及磁通密度波形

(5)

(6)

由式(6)可得出方波電壓激勵下磁通密度變化率，將所得公式代入式(1)，可得方波激勵下渦流和剩余損耗計算公式為：

(7)

(8)

將式(7)與正弦激勵下的渦流損耗計算公式相除，可得方波電壓激勵下渦流損耗修正系數為：

(9)

同理，方波激勵下剩余損耗修正系數為：

(10)

2.3.2 三角波激勵下損耗模型計算方法

三角波激勵時電壓與磁通密度在一個周期內隨時間變化波形如圖2所示，公式如式(11)和式(12)所示。

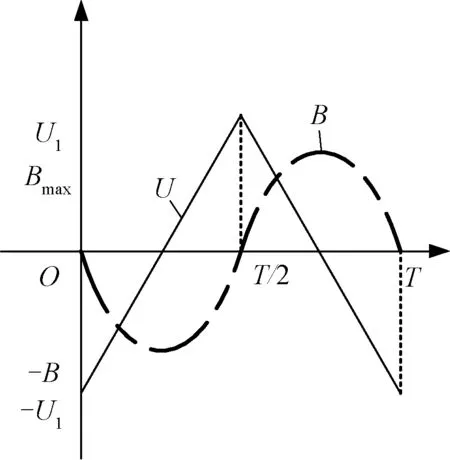
圖2 三角波電壓及磁通密度波形

(11)

(12)

由式(12)可得出三角波電壓激勵下磁通密度變化率，將所得公式代入式(1)，可得三角波電壓激勵下渦流和剩余損耗計算公式為：

(13)

(14)

將式(13)與正弦激勵下的渦流損耗計算公式相除，可得三角波電壓激勵下渦流損耗修正系數為：

(15)

同理可得三角波激勵下剩余損耗修正系數為：

(16)

引入渦流與剩余損耗修正系數，可以由正弦計算公式推導出非正弦激勵下損耗計算公式，公式如式(17)所示，表3為方波和三角波激勵下損耗修正系數。

(17)

表3 方波和三角波激勵下損耗模型修正系數

由表3可以觀察到，方波的渦流、剩余損耗修正系數均小于1，三角波渦流、剩余損耗系數均大于1，因此，可以推斷出在給定相同工作頻率與相同磁密峰值的條件下，三角波電壓激勵下的損耗數值最大，方波電壓激勵下的損耗數值最小。

3 磁性測量與分析

為了驗證第2節所提修正系數的有效性，對比分析非晶和納米晶材料的磁特性，得到不同工況下磁心的損耗數據，本文采用環形測量法，測量在正弦和非正弦激勵下磁心的損耗特性與磁特性，樣品為安泰公司生產的環形非晶與納米晶磁心。磁心原副邊線圈采用多股銅線并繞方式，以減少線圈內的趨膚效應。環形非晶磁心尺寸為外徑50 mm，內徑40 mm，高度為20 mm，帶材厚度為0.025 mm。環形納米晶磁心尺寸為外徑50 mm，內徑40 mm，高度為25 mm，帶材厚度為0.02 mm。

3.1 磁通密度控制方法

在實驗室搭建磁特性測試系統，測量正弦、方波及三角波在頻率范圍為1～10 kHz，不同磁通密度下的損耗值。實驗在空載條件下進行，測量系統由ARB波形編輯軟件、信號發生器WF1974、功率放大器NF4520、示波器、功率分析儀與非晶納米晶磁心組成。通過ARB波形編輯軟件編輯生成非正弦波，將所生成的非正弦波形信號傳遞給信號發生器。調節信號發生器可調節所施加激勵電壓與頻率的大小，將給定信息傳遞給功率放大器，功率放大器再將給定激勵施加給所試驗樣品。同時，功率分析儀記錄損耗數據，示波器記錄一次側電流與二次側感應電壓的波形，測量系統如圖3所示[13，14]。

圖3 磁特性測量系統

由法拉第電磁感應定律原理可求得感應電壓與磁通密度關系，關系如式(18)所示：

(18)

式中，u(t)為感應電壓，V；N為繞組匝數；S為磁心截面積，mm2。

將式(6)和式(12)進行求導并代入式(18),可推出在方波和三角波電壓激勵下，二次側感應電壓與磁通密度之間的關系如下所示。

方波電壓激勵下：

(19)

三角波電壓激勵下：

(20)

磁心一次側繞組所施加的激勵電壓控制磁心內部的激磁電流，激磁電流的改變引起激磁磁場發生變化。而激磁磁場的改變導致了磁心內磁通密度變化，由法拉第電磁感應定律可知，測量二次側感應電壓可以相應地測出磁心內部磁通密度，因此，在實際測量過程中，調節激勵電壓可以相應地控制磁心內部的磁通密度。

將二次側感應電壓進行積分，可得出在相應的感應電壓情況下磁心內磁通密度波形，波形如圖4所示。

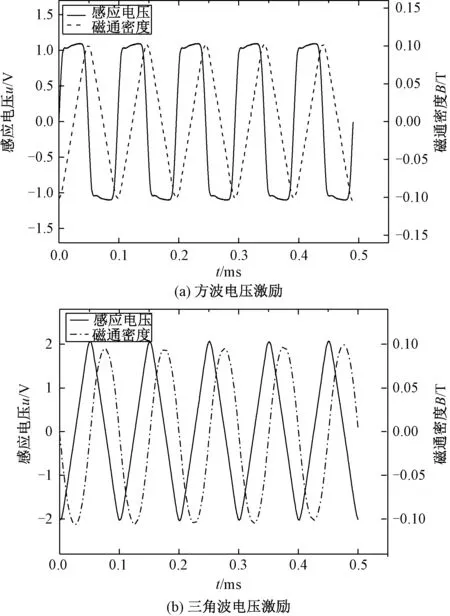
圖4 不同激勵下感應電壓與磁通密度波形

圖5 f=4 kHz時，不同磁通下非晶與納米晶磁滯回線

根據示波器保存的一次側電流與二次側感應電壓波形，處理波形數據可得，非晶和納米晶磁心在頻率為4 kHz，不同磁通密度時的磁滯回線如圖5所示。由圖5可知，納米晶磁心的矯頑力與磁滯回線面積小于非晶磁心，因此可以得出在相同工況下納米晶材料產生的損耗遠小于非晶材料，性能優越。但由于納米晶材料不易制取，價格昂貴，所以設計高頻變壓器時，應根據所需工況要求選擇材料類型。

3.2 對比分析

依據測量所得到的實驗數據，得到非晶磁心在正弦、方波與三角波電壓激勵下的損耗P與頻率變化關系如圖6所示。

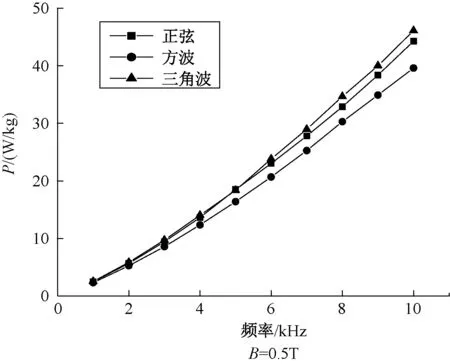
圖6 Bm=0.5 T時非晶磁心損耗與頻率關系

由圖6可以觀察到，磁心損耗大小與激勵電壓波形密切相關，在不同激勵下損耗數值不同。三角波電壓激勵下損耗數值最大，方波電壓激勵下損耗數值最小，驗證了上文所提出修正損耗系數的有效性。

4 損耗分離計算模型的改進

4.1 分離損耗

能準確地分離出磁滯損耗、渦流損耗和剩余損耗，是提取磁心損耗系數過程中的重要一步，本文采取如下步驟分離損耗。

(1)將式(2)左右兩邊同時除以頻率f，可以得到損耗W計算公式為：

(21)

(2)渦流損耗公式有明確的物理推導，所以，可以用渦流損耗公式來準確地計算磁心內的渦流損耗，因此將式(21)左邊減去渦流損耗計算值，得到磁滯損耗加剩余損耗的和如下所示：

(22)

由上述分離過程可以發現總損耗減去渦流耗后，損耗計算模型變為了與頻率的1/2次方有關的函數。基于W-f1/2函數的圖像特點，圖像的截距為H，圖斜率為L。因而，可以得到，磁滯損耗大小為H，剩余損耗大小為Lf1/2。經過數據處理與數據擬合可得到不同工況下的H與L，進而得到Kh與Kex的值。

4.2 損耗分離計算模型的改進

在進行上述分離損耗過程中發現，在不同工況下得到的損耗系數Kh與Kex不是固定值，會隨著磁通密度的改變而改變，考慮到高頻變壓器設計時所需精度的要求，在經典正弦模型的基礎上提出一種改進的損耗分離模型，計算公式如下所示：

(23)

式中，Kh(Bm)為磁滯損耗系數，Kh(Bm)=C0+C1Bm+C2Bm2+C3Bm3；Kex(Bm)為剩余損耗系數，Kex(Bm)=D0+D1Bm+D2Bm2+D3Bm3。

在式(23)的基礎上，分別代入第2節所推導三角波與方波修正系數，可得出方波與三角波激勵下損耗計算公式如下所示。

方波激勵下損耗計算公式為：

(24)

三角波激勵下損耗計算公式為：

(25)

式中，ξ1為方波激勵下渦流損耗修正系數；η1為方波激勵下剩余損耗系數；ξ2為三角波激勵下渦流損耗修正系數；η2為三角波激勵下剩余損耗系數。

在正弦激勵條件下非晶與納米晶的損耗系數Kh(Bm)和Kex(Bm)與磁通密度的關系如圖7和圖8所示，圖中非晶擬合的相關系數的值分別為0.984 5與0.989 1，納米晶擬合的相關系數的值分別為0.983 1與0.997 6，展現出了良好的相關性。

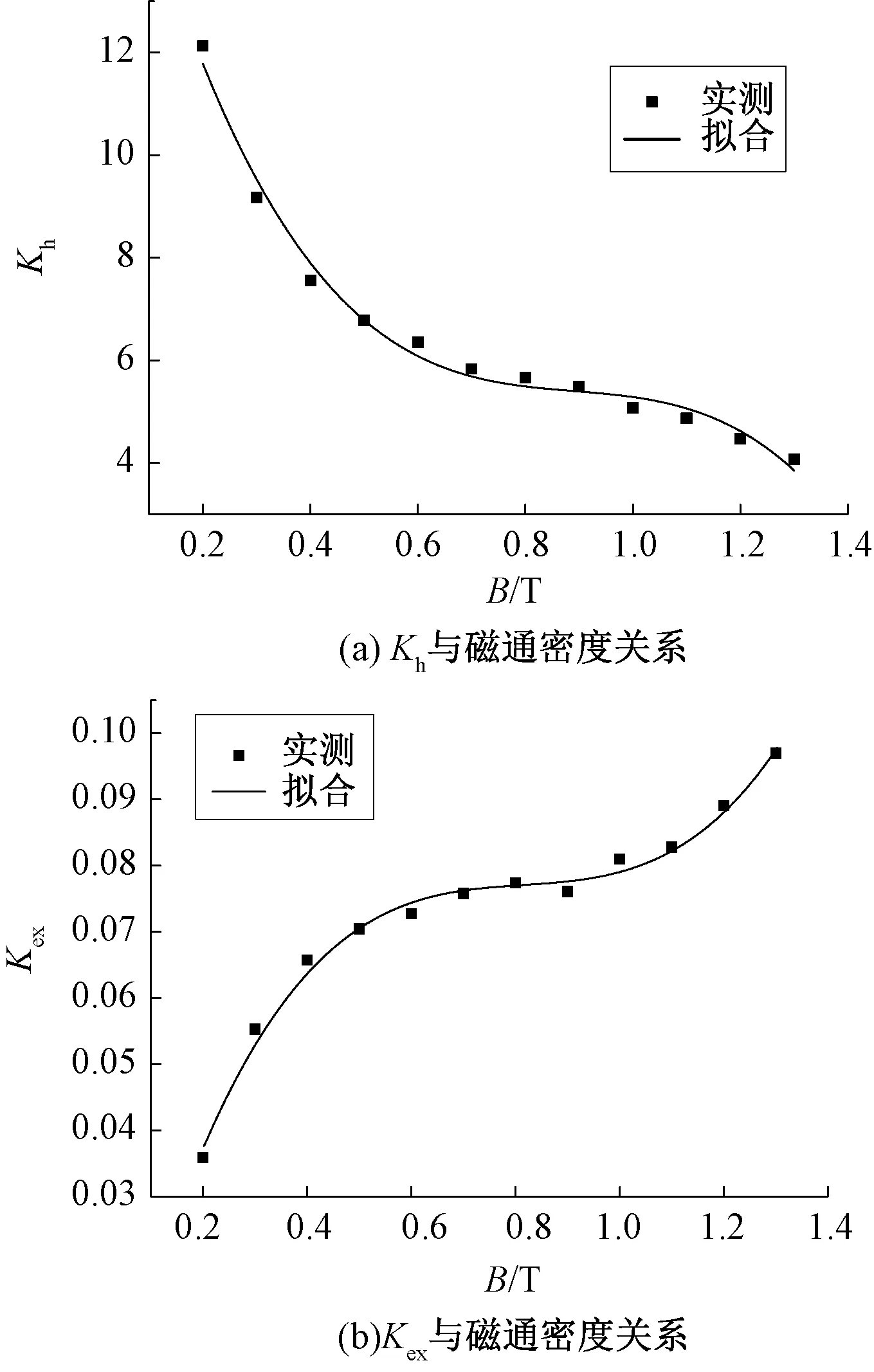
圖7 非晶磁心損耗系數與磁通密度關系

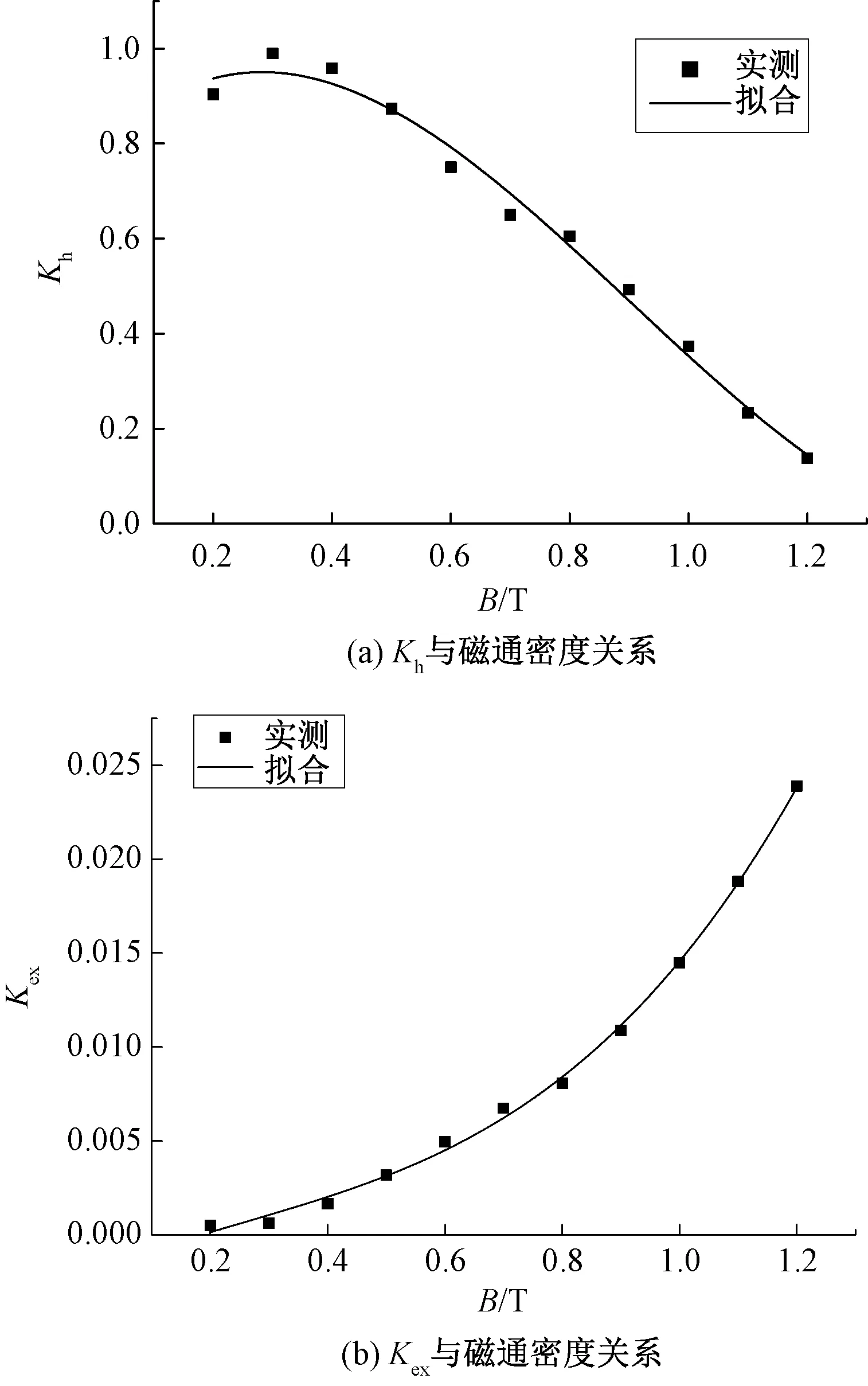
圖8 納米晶磁心損耗系數與磁通密度關系

因此，得到Kh(Bm)與Kex(Bm)公式中參數值大小如表4與表5所示。

表4 Kh(Bm)中的參數值

表5 Kex(Bm)中的參數值

4.3 改進損耗模型的驗證

為了檢驗本文所提出改進損耗分離計算模型的準確性，將改進模型的計算值與實驗值進行比較，誤差大小如表6所示。并將經典正弦損耗模型與改進正弦損耗模型的計算精度進行對比，結果如表7所示。

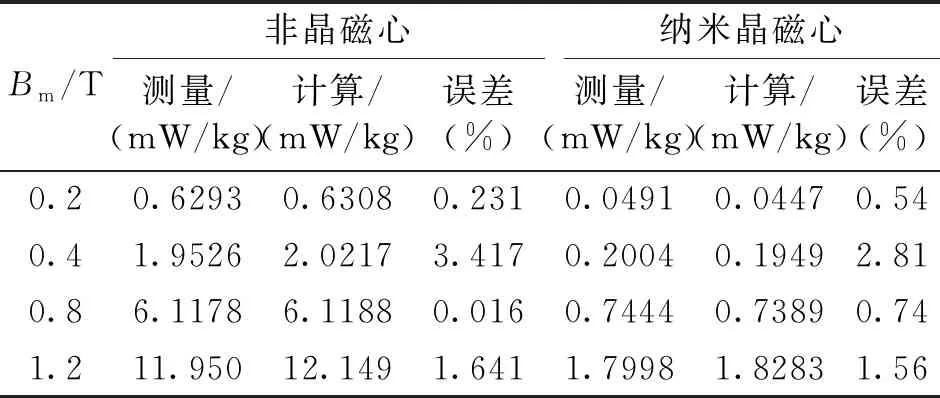
表6 改進損耗模型計算誤差

表7 經典損耗模型與改進損耗模型誤差對比

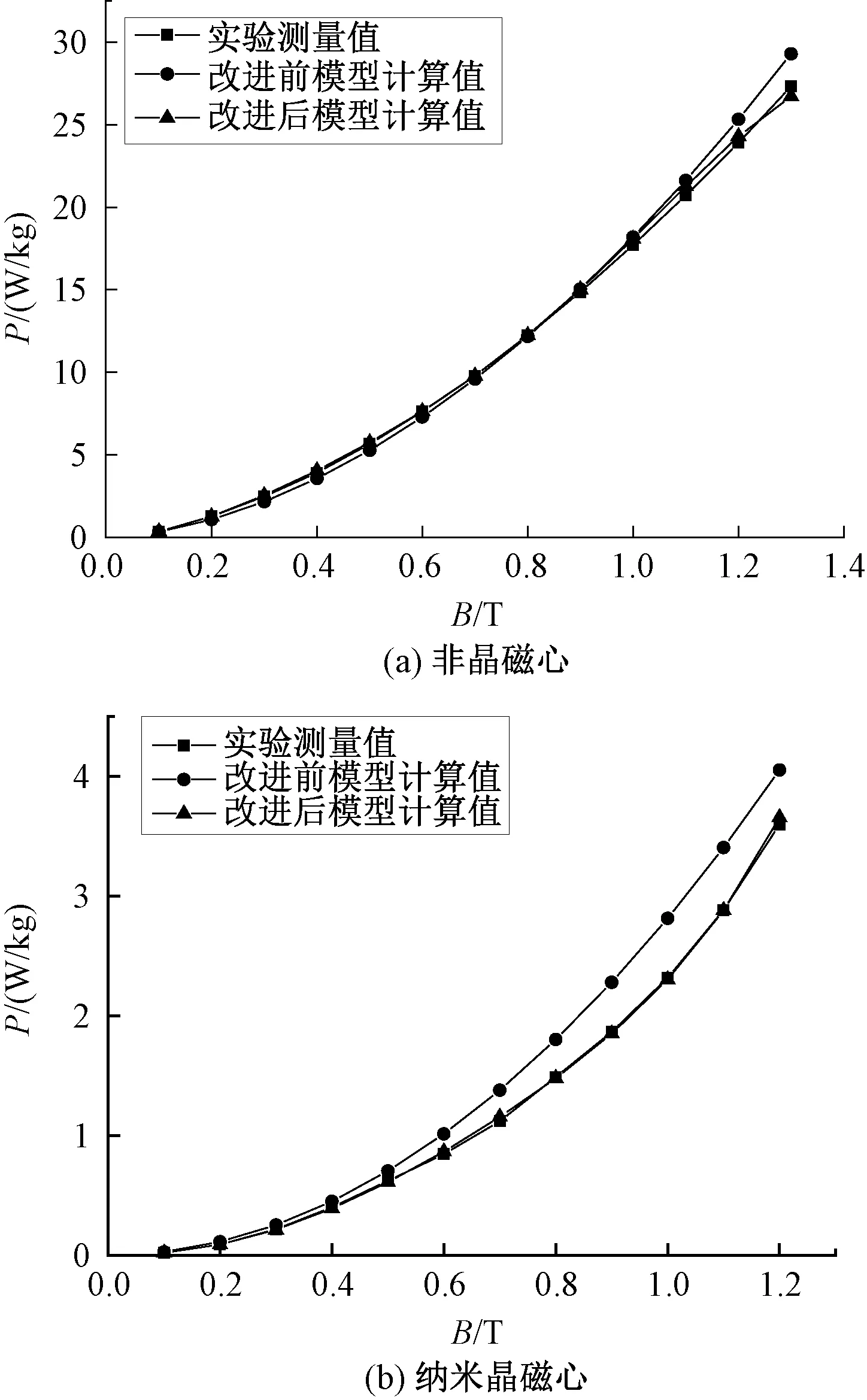
圖9 改進前與改進后模型損耗對比

由表7和圖9可知，在正弦電壓的激勵下，改進損耗分離模型的計算結果與經典損耗分離模型的計算結果相比與實驗數據吻合度更高，非晶與納米晶磁心的計算誤差均在8%以內，滿足精度要求。

非晶與納米晶磁心在方波和三角波激勵下的損耗可依照式(24)和式(25)進行計算，得到改進后非正弦損耗分離模型的計算結果與實驗數據對比如圖10所示。

圖10 f=2 kHz時改進后損耗模型計算值與測量值對比

由圖10可知，在方波與三角波電壓激勵下，非晶磁心與納米晶磁心改進后模型的計算結果與實驗數據誤差較小，契合度較高，驗證了文中所提出的改進損耗分離模型在非正弦電壓激勵下的有效性與準確性。

5 結論

本文在經典正弦損耗分離模型的基礎上，根據磁通波形特征推導出渦流損耗與剩余損耗修正系數，進而得到非正弦激勵下修正損耗分離計算模型。并依據損耗系數特征，提出一種改進損耗分離計算模型方法，提升了模型計算精度，并分別帶入損耗修正系數，得到非正弦激勵下改進的損耗模型，將改進后模型計算值與實驗值進行對比，發現模型有較好的契合度，檢驗了所提模型的可行性與有效性，對于精確計算高頻變壓器磁心損耗具有一定參考價值。