404 Not Found
404 Not Found
基于數(shù)據(jù)空間和稀疏約束的三維重力和重力梯度數(shù)據(jù)聯(lián)合反演
張镕哲, 李桐林, 劉財(cái)*, 李福元, 鄧馨卉, 石會(huì)彥
1 吉林大學(xué)地球探測(cè)科學(xué)與技術(shù)學(xué)院, 長(zhǎng)春 130026 2 中國(guó)地質(zhì)調(diào)查局廣州海洋地質(zhì)調(diào)查局, 廣州 510760 3 長(zhǎng)春工程學(xué)院, 長(zhǎng)春 130021
0 引言
重力探勘具有輕便、快捷、成本低等優(yōu)點(diǎn),已經(jīng)廣泛應(yīng)用于研究地殼內(nèi)部結(jié)構(gòu)、探明固體礦產(chǎn)和油氣資源分布等領(lǐng)域(Last and Kubik,1983;Guillen and Menichetti,1984;Li and Oldenburg,1998;Portniaguine and Zhdanov,1999;Nabighian et al.,2005;Silva and Barbosa,2006;Zhdanov,2009;Commer,2011). 隨著重力梯度全張量?jī)x(FTG)的問(wèn)世,人們不僅可以測(cè)量重力數(shù)據(jù),還可以測(cè)量重力梯度數(shù)據(jù). 重力數(shù)據(jù)是通過(guò)測(cè)量重力位的垂直一階導(dǎo)數(shù)獲得,而重力梯度數(shù)據(jù)是通過(guò)測(cè)量重力位在三個(gè)方向的二階導(dǎo)數(shù)獲得. 重力梯度數(shù)據(jù)包含多個(gè)分量信息,每個(gè)梯度分量包含的信息量不同,綜合利用各個(gè)分量信息有助于提高地質(zhì)解釋的準(zhǔn)確性(Vasco and Taylor,1991;Zhdanov et al.,2004;Martinez et al.,2013;陳閆等,2014;耿美霞等,2016;Zhang and Li,2019).
反演技術(shù)是地球物理勘探最為重要的定量解釋手段之一,它是通過(guò)地球物理異常場(chǎng)反推地下場(chǎng)源的空間分布情況,提供目標(biāo)地質(zhì)構(gòu)造的物性和幾何形態(tài)等特征信息.在頻率域中重力數(shù)據(jù)包含更多的低頻信息,對(duì)反映深層異常體細(xì)節(jié)方面具有更高的分辨率,而重力梯度數(shù)據(jù)包含更多的高頻信息,對(duì)反映淺層異常體細(xì)節(jié)方面具有更高的分辨率.根據(jù)兩種數(shù)據(jù)各自的特點(diǎn),結(jié)合兩種數(shù)據(jù)共同進(jìn)行反演計(jì)算,勢(shì)必會(huì)降低反演多解性和提高地質(zhì)解釋的可信性.Wu等(2013)將重力和重力梯度數(shù)據(jù)結(jié)合起來(lái),通過(guò)自適應(yīng)權(quán)值估計(jì)物體的質(zhì)量、方向和距離.Capriotti和Li(2014)針對(duì)重力和重力梯度數(shù)據(jù)核函數(shù)隨深度衰減速率不同的情況,在模型平滑約束項(xiàng)中加入權(quán)重平衡兩種衰減速率,實(shí)現(xiàn)了重力和重力梯度數(shù)據(jù)的平滑聯(lián)合反演.秦朋波和黃大年(2016)采用一種空間深度加權(quán)函數(shù),用來(lái)克服重力和重力梯度數(shù)據(jù)的趨膚效應(yīng),并通過(guò)有限內(nèi)存BFGS擬牛頓法求解重力和重力梯度數(shù)據(jù)的聯(lián)合反演.Qin等(2016)采用非線(xiàn)性共軛梯度法對(duì)重力和重力梯度數(shù)據(jù)開(kāi)展聯(lián)合反演研究,并將該算法應(yīng)用到美國(guó)墨西哥灣海岸鹽丘調(diào)查中.李紅蕾等(2017)提出了一種數(shù)據(jù)加權(quán)矩陣,實(shí)現(xiàn)了最小二乘迭代法的重力和重力梯度數(shù)據(jù)聯(lián)合反演,并應(yīng)用到青藏高原及鄰區(qū)巖石圈三維密度結(jié)構(gòu)預(yù)測(cè)中.高秀鶴等(2019)采用閾值約束的協(xié)克里金法對(duì)重力和重力梯度數(shù)據(jù)進(jìn)行了聯(lián)合反演研究.根據(jù)上述研究發(fā)現(xiàn),目前重力和重力梯度聯(lián)合反演算法仍存在以下幾點(diǎn)問(wèn)題,首先,采用平滑約束模型矩陣得到的反演結(jié)果過(guò)于模糊發(fā)散,不能很好地恢復(fù)出真實(shí)模型的尖銳邊界;然后,引入依賴(lài)先驗(yàn)信息的深度加權(quán)函數(shù),需要人為經(jīng)驗(yàn)來(lái)確定參數(shù)變量的大小,具有一定的不確定性;其次,采用傳統(tǒng)的最小二乘迭代法需要計(jì)算和存儲(chǔ)靈敏度矩陣,尤其在三維大數(shù)據(jù)情況下,靈敏度矩陣會(huì)占用大量的內(nèi)存空間,而共軛梯度法會(huì)出現(xiàn)連續(xù)搜索小步長(zhǎng)的現(xiàn)象,增加反演的迭代次數(shù),從而降低反演的計(jì)算效率.最后,在模型空間下求解三維聯(lián)合反演時(shí),求解的線(xiàn)性方程組維度較大,勢(shì)必會(huì)增加大量的計(jì)算時(shí)間和內(nèi)存消耗量,并對(duì)計(jì)算機(jī)的性能提出挑戰(zhàn).
針對(duì)上述問(wèn)題,本文提出了基于數(shù)據(jù)空間和稀疏約束的重力和重力梯度數(shù)據(jù)聯(lián)合反演算法.首先,我們從基于幾何格架的重力快速正演算法出發(fā),推導(dǎo)出多分量重力梯度數(shù)據(jù)的快速正演算法.然后,構(gòu)建了重力和重力梯度數(shù)據(jù)聯(lián)合反演目標(biāo)函數(shù),目標(biāo)函數(shù)中包含了重力和重力梯度數(shù)據(jù)擬合項(xiàng)、L0范數(shù)正則化模型約束項(xiàng),模型約束項(xiàng)中摒棄了依賴(lài)先驗(yàn)信息的深度加權(quán)函數(shù),引入了自適應(yīng)模型積分靈敏度矩陣來(lái)克服趨膚效應(yīng).其次,將模型計(jì)算從模型空間通過(guò)恒等式轉(zhuǎn)換到數(shù)據(jù)空間下,采用一種改進(jìn)的共軛梯度算法進(jìn)行反演求解,可以降低反演求解方程的維度和避免存儲(chǔ)大型的靈敏度矩陣.最后,通過(guò)模型試算和實(shí)測(cè)數(shù)據(jù)驗(yàn)證本文提出算法的準(zhǔn)確性和有效性.
1 快速正演計(jì)算理論
將地下目標(biāo)空間劃分為一系列大小相同的長(zhǎng)方體網(wǎng)格單元,且每個(gè)長(zhǎng)方體單元的密度均勻, 此時(shí)地表重力數(shù)據(jù)或重力梯度張量數(shù)據(jù)與地下密度分布可以表示為如下線(xiàn)性關(guān)系:
d=A·m,
(1)
其中:d為重力或重力梯度數(shù)據(jù);A為重力數(shù)據(jù)或重力梯度數(shù)據(jù)的正演核函數(shù),是一個(gè)Nd×Nm的矩陣,其中Nd為觀(guān)測(cè)點(diǎn)個(gè)數(shù),Nm為地下模型網(wǎng)格剖分個(gè)數(shù);m為網(wǎng)格單元的剩余密度.
重力或重力梯度正演計(jì)算需要完成的積分次數(shù)為Nd×Nm,當(dāng)?shù)叵戮W(wǎng)格剖分過(guò)大時(shí),正演計(jì)算將面臨巨大的挑戰(zhàn).為了提高正演的計(jì)算效率,本文采用姚長(zhǎng)利等(2003)提出的幾何格架的快速計(jì)算策略,通過(guò)分析地下模型單元與觀(guān)測(cè)點(diǎn)之間的位置關(guān)系,可以發(fā)現(xiàn)同一層各模型單元與觀(guān)測(cè)點(diǎn)之間的相對(duì)位置關(guān)系存在等價(jià)性,利用這個(gè)等價(jià)關(guān)系,只對(duì)每一層第一個(gè)模型單元進(jìn)行幾何格架核函數(shù)計(jì)算,得到該單元的核函數(shù)矩陣,而該層其他模型單元的核函數(shù)矩陣可以通過(guò)幾何格架的等效性進(jìn)行查找獲得.通過(guò)上述方法,原本反演過(guò)程中需要多次重復(fù)進(jìn)行的正演計(jì)算就變成了物性參數(shù)與對(duì)應(yīng)的幾何格架之間簡(jiǎn)單的乘積運(yùn)算,每層模型單元只計(jì)算第一個(gè)模型單元,從而大大的提高了正演的計(jì)算效率.具體思想如下:
地下模型均勻剖分,觀(guān)測(cè)點(diǎn)位于模型單元中心正上方的地表處,如圖1所示.假設(shè)地表觀(guān)測(cè)面上任意一個(gè)觀(guān)測(cè)點(diǎn)p(u,v)(u=1,2,3,…,Nx;v=1,2,3,…,Ny,Nx和Ny分別為x軸和y軸方向上的觀(guān)測(cè)點(diǎn)個(gè)數(shù))與地下第kk層模型單元Qkk(u,v)對(duì)應(yīng)(kk=1,2,3,…,L,L為地下模型的層數(shù)).首先需要求取第kk層第一個(gè)模型單元Qkk(1,1)在觀(guān)測(cè)點(diǎn)p(u,v)處的幾何格架核矩陣Akk(1,1,u,v),然后根據(jù)幾何格架的平移等效性、對(duì)稱(chēng)互換性可以得到第kk層其他模型單元Qkk(i,j)(i=1,2,3,…,Nx;j=1,2,3,…,Ny)在觀(guān)測(cè)點(diǎn)p(u,v)處的幾何格架核函數(shù)矩陣Akk(i,j,u,v).
tt=|u-i|+1,pp=|v-j|+1.
(2)
Akk(i,j,u,v)=Akk(1,1,tt,pp).
(3)
為了簡(jiǎn)約起見(jiàn),將公式(3)改寫(xiě)為一維列向量:
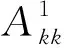
(4)
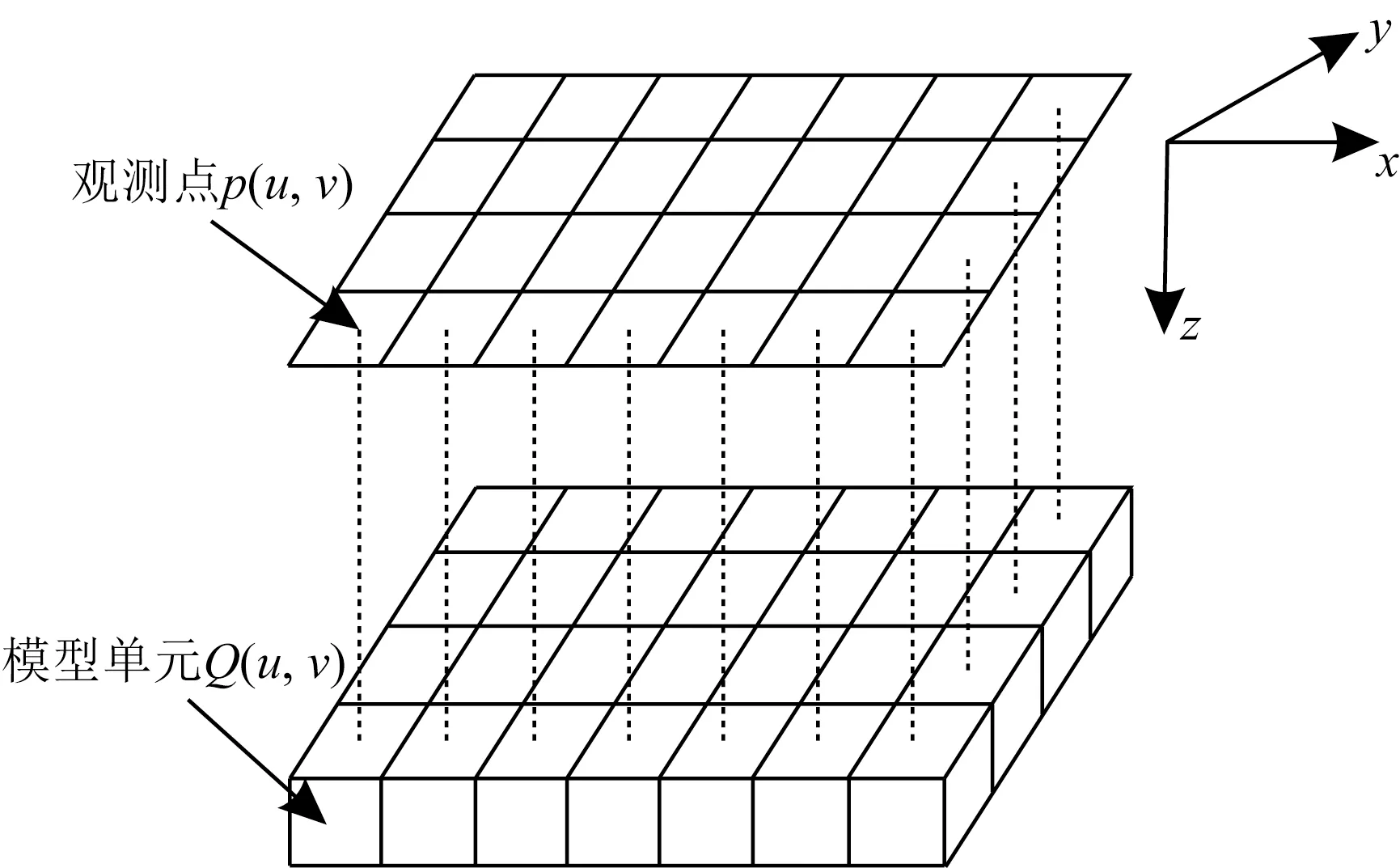
圖1 三維模型網(wǎng)格剖分圖Fig.1 3D model meshing
上述幾何格架計(jì)算策略?xún)H適用于重力的核函數(shù)計(jì)算,而將上述方法應(yīng)用到重力梯度多分量時(shí),非對(duì)角線(xiàn)重力梯度分量(Vxy,Vzy,Vzx)將得不到正確的核函數(shù)矩陣.通過(guò)實(shí)驗(yàn)?zāi)M分析,模型單元的位置與觀(guān)測(cè)點(diǎn)的位置處于特殊關(guān)系時(shí),公式(4)將不再成立.我們將幾何格架等效關(guān)系式進(jìn)行修改, 重力梯度非對(duì)角線(xiàn)分量的幾何格架關(guān)系式可表示為:
對(duì)于分量Vzx:
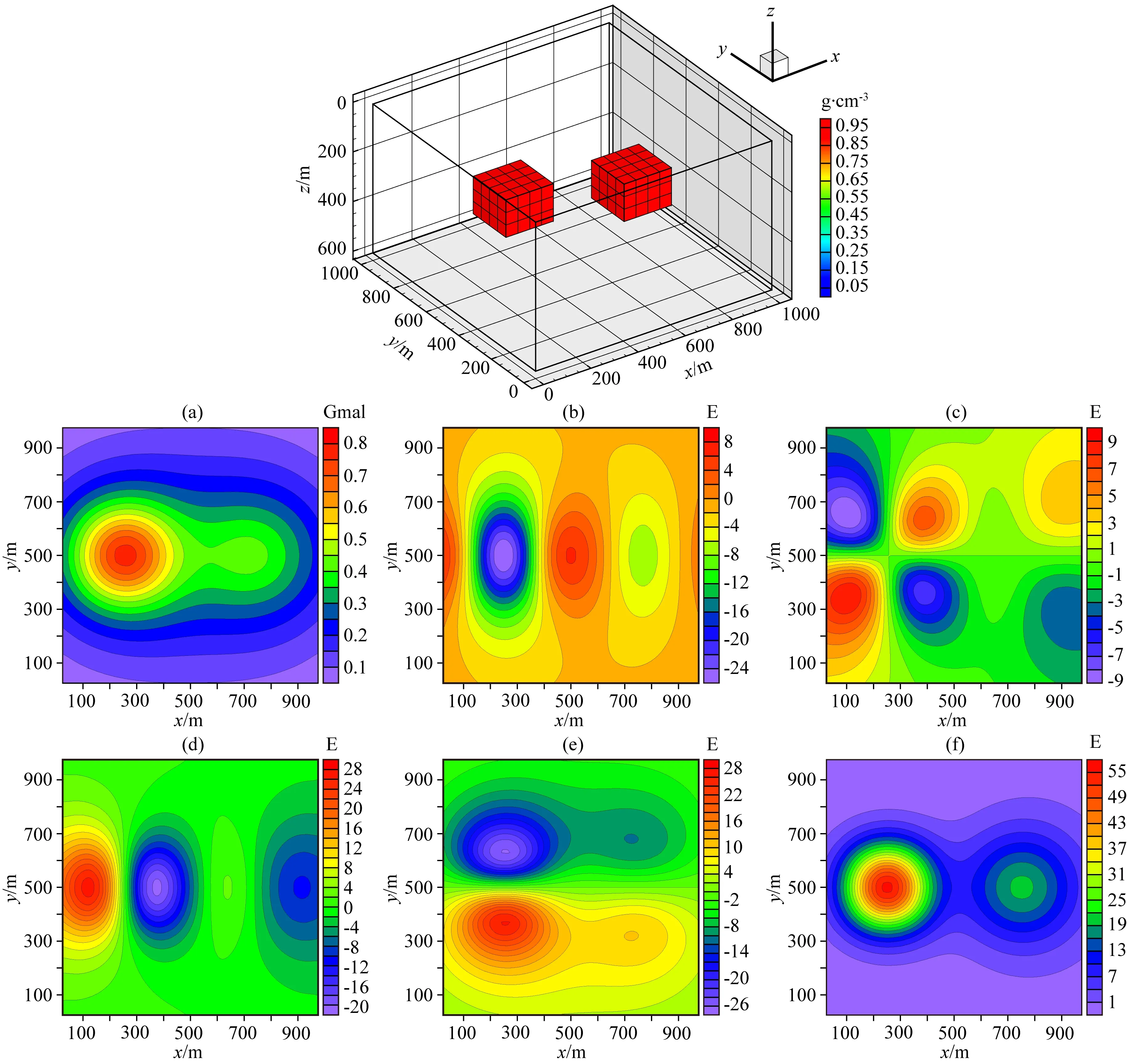
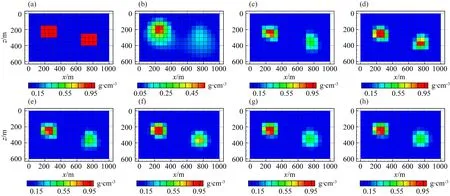
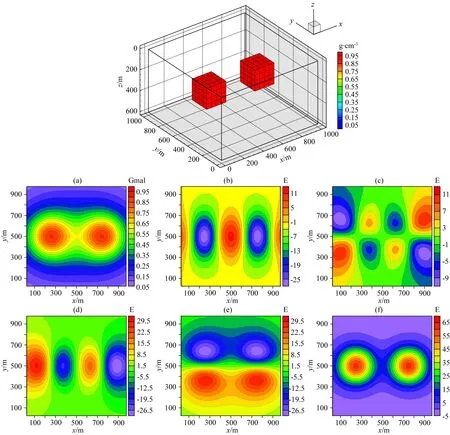
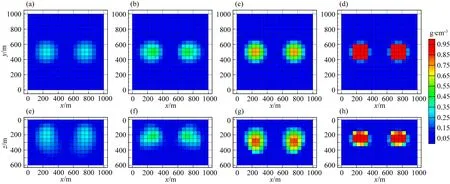
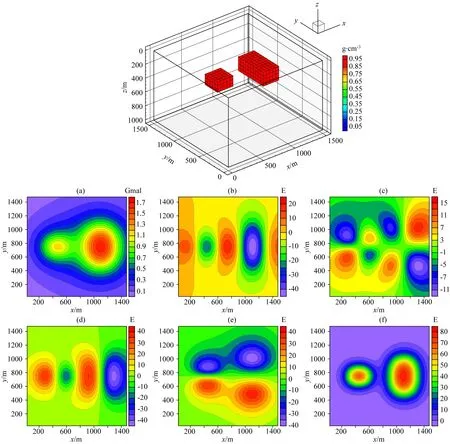
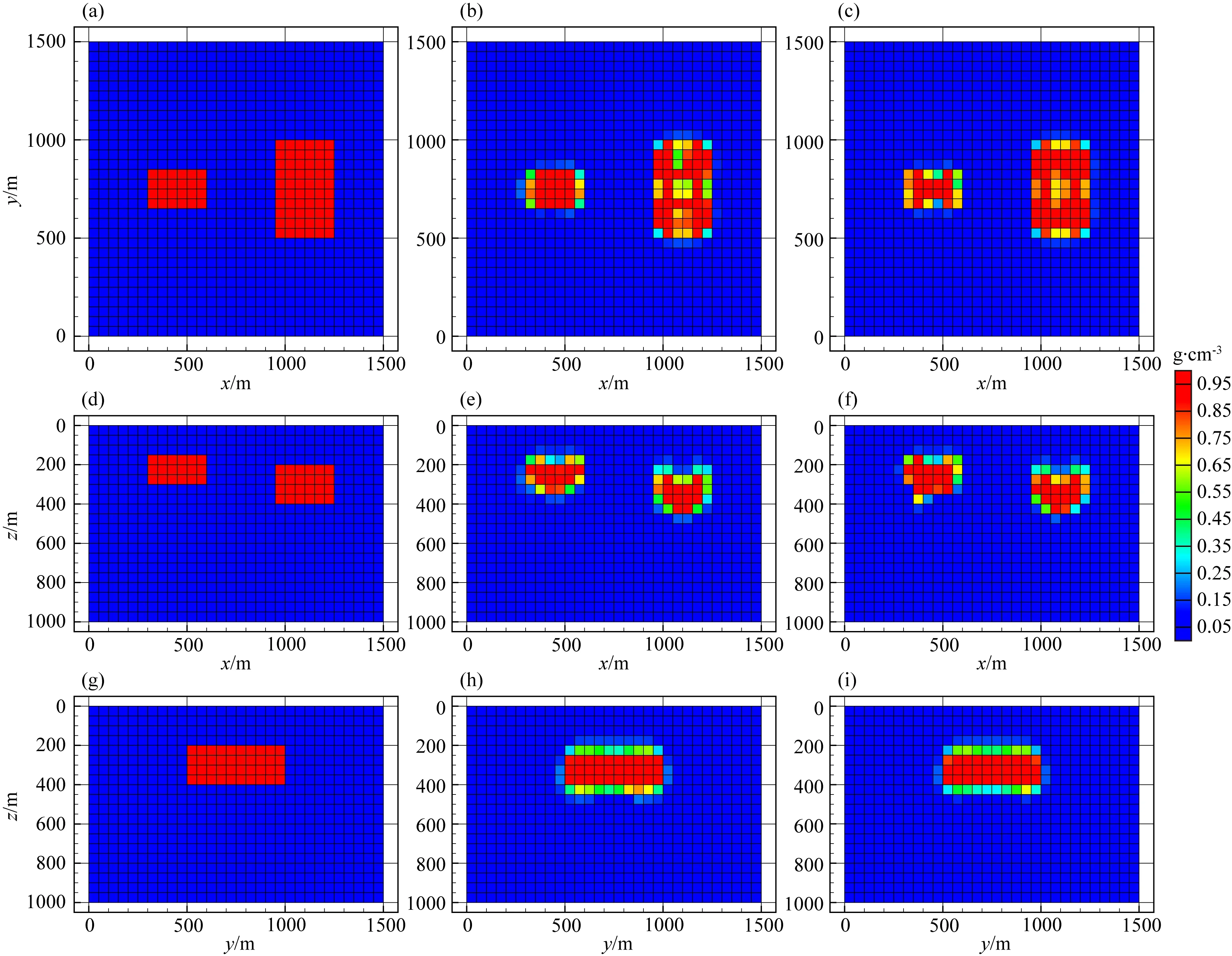
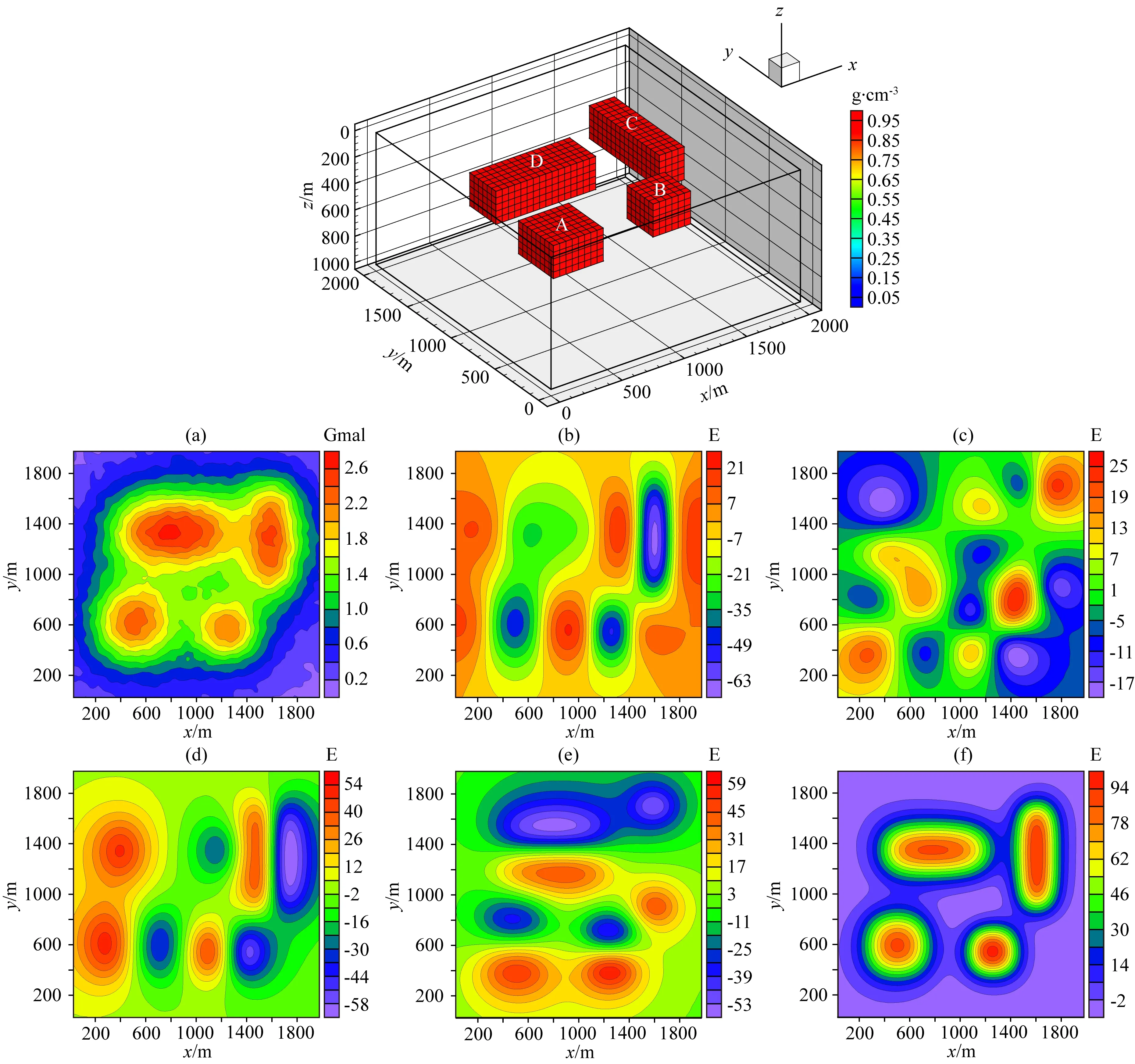
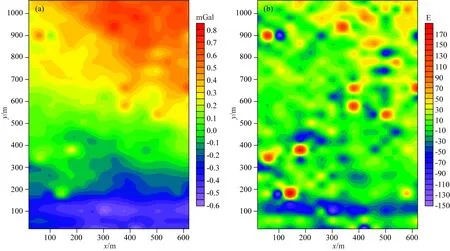
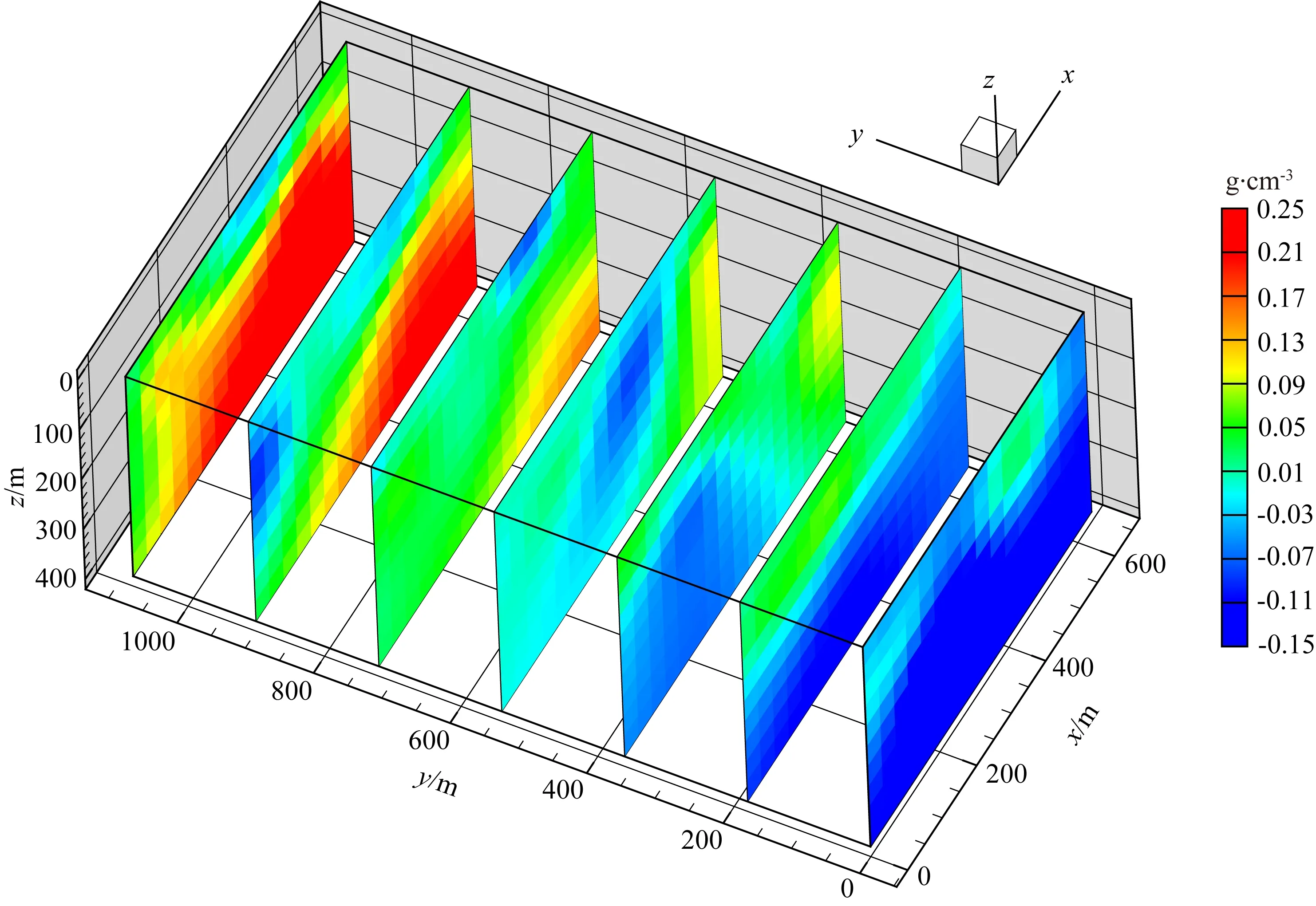
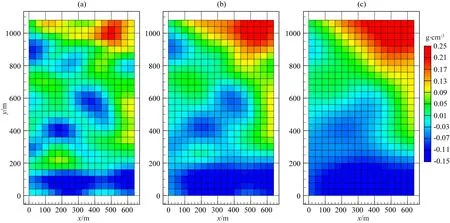
ifu end 對(duì)于分量Vzy: ifv end 對(duì)于分量Vxy: ifu ifu end end 為了避免因求解病態(tài)反問(wèn)題所引起的不穩(wěn)定性和多解性等問(wèn)題,本文采用Tikhonov和Arsenin(1977)正則化方法求解反演線(xiàn)性方程.首先,我們構(gòu)建重力和重力梯度數(shù)據(jù)聯(lián)合反演目標(biāo)函數(shù),其表達(dá)式如下: Φ(m)=Φd(m)+α·Φm(m), (5) 其中,Φd(m)為數(shù)據(jù)擬合項(xiàng),Φm(m)為穩(wěn)定器構(gòu)成目標(biāo)函數(shù)中的模型約束項(xiàng),α為正則化因子. 目標(biāo)函數(shù)中數(shù)據(jù)擬合項(xiàng)包括兩部分, (6) 將數(shù)據(jù)擬合項(xiàng)進(jìn)行簡(jiǎn)化, Φd(m)=‖WqWd(dobs-Am)‖2, (7) (8) L0范數(shù)正則化模型約束項(xiàng)的表達(dá)式如下: (9) 求解公式(9)可以將L0范數(shù)最小化近似為迭代重加權(quán)L2范數(shù)最小化問(wèn)題(Wolke and Schwetlick,1988). Φm(m)=‖Wmm‖2, (10) (11) 其中,ε是很小的常數(shù),該參數(shù)決定了反演結(jié)果的尖銳程度.與傳統(tǒng)的平滑反演方法相比,基于稀疏約束的L0范數(shù)反演方法可以獲得邊界更清晰、對(duì)比度更強(qiáng)的模型.將L0范數(shù)作為模型約束項(xiàng),目標(biāo)函數(shù)表達(dá)式可以表示為: Φ(m)=‖WqWd(dobs-Am)‖2 +α·‖Wm(m-mref)‖2, (12) 其中,mref為參考模型.利用公式(12)求解的反演結(jié)果會(huì)出現(xiàn)異常體集中在地表的現(xiàn)象,是由于重力和重力梯度數(shù)據(jù)的核函數(shù)隨深度增加而衰減,因此會(huì)引起反演結(jié)果的趨膚效應(yīng).為了改善趨膚效應(yīng)的影響,傳統(tǒng)的方法是在模型約束項(xiàng)中加入深度加權(quán)函數(shù)(Li and Oldenburg,1996;Commer,2011),但是重力和重力梯度核函數(shù)衰減速率不同,采用相同的深度加權(quán)函數(shù)勢(shì)必會(huì)得到不準(zhǔn)確的反演結(jié)果,況且深度加權(quán)函數(shù)中存在未知的變量,需要人為經(jīng)驗(yàn)來(lái)定義變量的大小,具有一定的不確定性和不穩(wěn)定性.針對(duì)上述問(wèn)題,Zhdanov (2002)提出了模型積分靈敏度矩陣,它可以消除不同模型參數(shù)對(duì)觀(guān)測(cè)數(shù)據(jù)的貢獻(xiàn)是不同的,觀(guān)測(cè)數(shù)據(jù)對(duì)不同模型參數(shù)的積分靈敏度也是不同所帶來(lái)的影響,使得觀(guān)測(cè)數(shù)據(jù)對(duì)不同模型參數(shù)的積分靈敏度變化一致.目前該方法已經(jīng)應(yīng)用在重力梯度三維反演中(陳閆,2014;Capriotti and Li,2014;高秀鶴和黃大年,2017).本文也采用模型積分靈敏度矩陣,用來(lái)消除因重力和重力梯度核函數(shù)衰減速率不同引起的趨膚效應(yīng).因此,仍然是形成一個(gè)權(quán)重,平衡重力和重力梯度兩個(gè)核函數(shù)衰減速率不同的問(wèn)題. 首先分析模型參數(shù)mk的微擾對(duì)數(shù)據(jù)的影響.觀(guān)測(cè)數(shù)據(jù)與模型參數(shù)變化的關(guān)系可表示為: δdi=Aikδmk, (13) 數(shù)據(jù)靈敏度對(duì)模型參數(shù)mk的積分可表示為: (14) 故模型積分靈敏度矩陣可表示為: (15) 將式(15)加入到目標(biāo)函數(shù)中,最終得到重力梯度和重力數(shù)據(jù)聯(lián)合反演的目標(biāo)函數(shù)表達(dá)式如下: Φ(m)=‖WqWd(dobs-Am)‖2 +α·‖WmS(m-mref)‖2. (16) 通常目標(biāo)函數(shù)最優(yōu)化方法是采用最小二乘法,即目標(biāo)函數(shù)對(duì)模型參數(shù)的求導(dǎo)為零,得到反演模型結(jié)果.但最小二乘法存在一定的缺陷,很容易陷入局部極小,求解不準(zhǔn)確,所以一些非線(xiàn)性?xún)?yōu)化方法經(jīng)常被使用,例如,牛頓法、梯度法、高斯牛頓法、共軛梯度法等.共軛梯度法對(duì)初始模型要求較少,具有存儲(chǔ)量小、收斂速度快等優(yōu)勢(shì).傳統(tǒng)的共軛梯度法迭代求解過(guò)程是在同一個(gè)循環(huán)內(nèi)完成,而本文采用內(nèi)外雙循環(huán)的迭代過(guò)程進(jìn)行目標(biāo)函數(shù)的求解,該方法可以減少迭代次數(shù),提高計(jì)算效率. 2.2.1 傳統(tǒng)共軛梯度法反演 對(duì)目標(biāo)函數(shù)公式(16)求梯度,得到第k次迭代的梯度表達(dá)式: (17) 準(zhǔn)備觀(guān)測(cè)數(shù)據(jù)dobs,數(shù)據(jù)加權(quán)矩陣Wd,初始模型m0,模型積分靈敏度矩陣S和數(shù)據(jù)加權(quán)項(xiàng)Wq,初始正則化參數(shù)α0. 計(jì)算目標(biāo)函數(shù)初始梯度g0和RR0; Whilek k=k+1; 更新模型參數(shù):mk=mk-1-tk-1dk-1; 計(jì)算數(shù)據(jù)擬合差: 計(jì)算目標(biāo)函數(shù)對(duì)模型mk的梯度gk和RRk; end While 輸出mk. 2.2.2 改進(jìn)的共軛梯度法反演 對(duì)目標(biāo)函數(shù)公式(16)求極值,得到第k次迭代的高斯-牛頓法模型改變量表達(dá)式: Δmk=mk-mk-1=(Rk)-1bk, (18) 準(zhǔn)備觀(guān)測(cè)數(shù)據(jù)dobs,數(shù)據(jù)加權(quán)矩陣Wd,初始模型m0,模型積分靈敏度矩陣S和數(shù)據(jù)加權(quán)項(xiàng)Wq,初始正則化參數(shù)α0. Whilek 計(jì)算Rk和bk; 令x0=0,r0=d0=bk; i=i+1; 更新參數(shù):xi=xi-1+ti-1di-1; ri=ri-1-ti-1Rkdi-1; end While k=k+1; mk=mk-1+xi; 計(jì)算數(shù)據(jù)擬合差: end While 輸出mk. 數(shù)據(jù)空間法(Siripunvaraporn and Egbert, 2000; Siripunvaraporn et al., 2005)是將模型計(jì)算從模型空間通過(guò)恒等式轉(zhuǎn)換到數(shù)據(jù)空間下進(jìn)行求解.由于模型個(gè)數(shù)Nm遠(yuǎn)遠(yuǎn)大于數(shù)據(jù)個(gè)數(shù)Nd,反演計(jì)算屬于欠定問(wèn)題,采用模型空間法進(jìn)行反演計(jì)算需要求解一個(gè)Nm×Nm的方程組,而在數(shù)據(jù)空間中只需要求解一個(gè)Nd×Nd的方程組,因此可以有效地降低反演計(jì)算的內(nèi)存占用量和計(jì)算時(shí)間(Pilkington, 2009; 李澤林, 2015; Zhang and Li, 2019; Zhang et al., 2020).本文將模型空間下的模型改變量表達(dá)式(18)轉(zhuǎn)換為數(shù)據(jù)空間下的模型改變量表達(dá)式: (19) 對(duì)高斯-牛頓法推導(dǎo)出的模型改變量表達(dá)式(19)直接求解,雖然可以降低反演計(jì)算的維度,但是需要存儲(chǔ)靈敏度矩陣A,在三維情況下勢(shì)必也會(huì)產(chǎn)生大量的計(jì)算內(nèi)存和時(shí)間.本文采用改進(jìn)的共軛梯度反演方法求解數(shù)據(jù)空間下的模型改變量,令Rk= 正則化因子的選取與Portniaguine和Zhdanov(2002)采用的方法相同,初始正則化因子α0=0.1. 隨著迭代的增加,模型約束項(xiàng)可能會(huì)增加,為了確保目標(biāo)函數(shù)的收斂在全區(qū)最小,此時(shí)需要修正正則化因子,表達(dá)式如下: (20) (21) 為了保障聯(lián)合反演迭代收斂,我們會(huì)在擬合差增大或擬合差變化緩慢時(shí),按比例減小正則化因子. αk+1=αkq, (22) 其中,q為縮放因子,設(shè)q= 0.6. 為了證明重力與重力梯度數(shù)據(jù)聯(lián)合反演優(yōu)于單獨(dú)重力數(shù)據(jù)反演,我們?cè)O(shè)計(jì)了一個(gè)不同高度相同大小的雙異常體組合模型,如圖2所示.異常體的大小都為200 m×200 m×150 m,剩余密度為1 g·cm-3.地下模型空間尺度x,y,z為1000 m×1000 m×600 m,將地下模型剖分為20×20×12個(gè)緊密排列的規(guī)則立方體單元,每個(gè)單元大小為50 m×50 m×50 m,背景剩余密度為0 g·cm-3.地面觀(guān)測(cè)點(diǎn)個(gè)數(shù)為20×20,觀(guān)測(cè)點(diǎn)位于網(wǎng)格中心,正演計(jì)算的觀(guān)測(cè)重力和重力梯度數(shù)據(jù)如圖2所示. 表1 反演模型和理論模型的均方根誤差Table 1 The root mean square error of each inversion model and the theoretical model 圖2 模型一的理論模型和正演響應(yīng)等值線(xiàn)圖(a) 重力gz; (b) 重力梯度分量Vxx; (c) 重力梯度分量Vxy; (d) 重力梯度分量Vzx; (e) 重力梯度分量Vzy; (f) 重力梯度分量Vzz.Fig.2 Theoretical model and forward response contour map of model 1(a) Gravity gz; (b) Gravity gradient component Vxx; (c) Gravity gradient component Vxy ; (d) Gravity gradient component Vzx; (e) Gravity gradient component Vzy ; (f) Gravity gradient component Vzz . 圖3 不同觀(guān)測(cè)數(shù)據(jù)反演結(jié)果對(duì)比圖(a) 理論模型; (b) gz反演結(jié)果; (c) gz和Vxx聯(lián)合反演結(jié)果; (d) gz和Vxy聯(lián)合反演結(jié)果; (e) gz和Vzx聯(lián)合反演結(jié)果; (f) gz和Vzy聯(lián)合反演結(jié)果; (g) gz和Vzz聯(lián)合反演結(jié)果; (h) gz和全張量聯(lián)合反演結(jié)果; 垂向切片位于y=550 m處.Fig.3 Comparison of different observation data inversion results(a) Theoretical model; (b) gz inversion results; (c) gz and Vxx joint inversion results; (d) gz and Vxy joint inversion results; (e) gz and Vzx joint inversion results; (f) gz and Vzy joint inversion results; (g) gz and Vzz joint inversion results; (h) gz and full tensor joint inversion results; The cross section is located at y=550 m. 為了驗(yàn)證改進(jìn)的共軛梯度法更適合應(yīng)用于重力和重力梯度數(shù)據(jù)的聯(lián)合反演,我們建立了一個(gè)雙異常體組合模型,如圖4所示.模型中包含了兩個(gè)大小相同的異常體,兩個(gè)異常體的大小為200 m×200 m×200 m,剩余密度為1 g·cm-3,埋深均為150 m,相距300 m.地下空間網(wǎng)格剖分和觀(guān)測(cè)方式與模型一完全相同,正演計(jì)算的觀(guān)測(cè)重力和重力梯度數(shù)據(jù)如圖4所示. 圖4 模型二的理論模型和正演響應(yīng)等值線(xiàn)圖(a) 重力gz; (b) 重力梯度分量Vxx; (c) 重力梯度分量Vxy; (d) 重力梯度分量Vzx; (e) 重力梯度分量Vzy; (f) 重力梯度分量Vzz.Fig.4 Theoretical model and forward response contour map of model 2(a) Gravity gz; (b) Gravity gradient component Vxx; (c) Gravity gradient component Vxy; (d) Gravity gradient component Vzx; (e) Gravity gradient component Vzy; (f) Gravity gradient component Vzz. 分別對(duì)傳統(tǒng)和改進(jìn)共軛梯度算法進(jìn)行重力和重力梯度數(shù)據(jù)聯(lián)合反演計(jì)算,兩種方法都選擇模型積分靈敏度矩陣,初始模型均采用半空間為0 g·cm-3的剩余密度模型.為了獲得更穩(wěn)定的反演結(jié)果,傳統(tǒng)共軛梯度法反演需要在加權(quán)模型參數(shù)域下求解,反演經(jīng)過(guò)48次迭代達(dá)到擬合差閾值1以下,耗時(shí)290 s,獲得的反演結(jié)果切片如圖5(b,e,h)所示.而改進(jìn)共軛梯度法反演經(jīng)過(guò)4次迭代達(dá)到擬合差閾值1以下,耗時(shí)70 s,獲得的反演結(jié)果切片如圖5(c,f,i)所示.可以發(fā)現(xiàn),兩種方法都可以恢復(fù)出異常體的中心位置和幾何大小,但是傳統(tǒng)共軛梯度法反演結(jié)果邊界更模糊,而改進(jìn)的共軛梯度法反演結(jié)果聚焦程度更高,異常體邊界更清晰.無(wú)論是在計(jì)算時(shí)間方面,還是在反演結(jié)果分辨率方面,改進(jìn)的共軛梯度法反演都具有明顯的優(yōu)勢(shì),更適合于三維重力和重力梯度聯(lián)合反演計(jì)算. 圖5 傳統(tǒng)和改進(jìn)的共軛梯度法反演結(jié)果對(duì)比圖(a,d,g) 理論模型; (b,e,h) 傳統(tǒng)的共軛梯度法反演結(jié)果; (c,f,i) 改進(jìn)的共軛梯度法反演結(jié)果; (a,b,c) z=300 m處的橫向切片; (d,e,f) y=500 m處的垂向切片; (g,h,i) x=250 m處的垂向切片圖.Fig.5 Comparison of traditional and improved conjugate gradient inversion results(a,d,g) Theoretical model; (b,e,h) Traditional conjugate gradient inversion results; (c,f,i) Improved conjugate gradient inversion results; (a,b,c) In the z=300 m depth section; (d,e,f) In the y=500 m cross section; (g,h,i) In the x=250 m cross section. 為了驗(yàn)證模型積分靈敏度矩陣相比于深度加權(quán)矩陣,可以更有效的消除因重力和重力梯度核函數(shù)衰減速率不同引起的趨膚效應(yīng),我們繼續(xù)選用模型二進(jìn)行重力和重力梯度數(shù)據(jù)聯(lián)合反演試算.將公式(16)中的S矩陣選取深度加權(quán)矩陣(Li and Oldenburg,1996)和模型積分靈敏度矩陣分別進(jìn)行平滑和稀疏約束反演.所有反演方法最終的擬合差均收斂到閾值0.1以下,反演結(jié)果如圖6所示.圖6(a,e)和圖6(b,f)分別為加入深度加權(quán)矩陣后的平滑和稀疏約束反演結(jié)果切片圖,可以發(fā)現(xiàn),反演異常體的中心位置與真實(shí)異常體存在一定的差異,由于趨膚效應(yīng),中心位置有上移的趨勢(shì),并且異常體的物性參數(shù)值要遠(yuǎn)小于真實(shí)值.圖6(c,g)和圖6(d,h)分別為加入模型積分靈敏度矩陣后的平滑和稀疏約束反演結(jié)果切片圖,由于模型積分靈敏度矩陣的加入,反演異常體物性參數(shù)值得到了明顯地改善,并且異常體中心下移,有效地克服了核函數(shù)衰減引起的趨膚效應(yīng).模型積分靈敏度矩陣與稀疏約束反演相結(jié)合,反演得到的結(jié)果無(wú)論是幾何形態(tài)還是物性參數(shù)值方面,都與真實(shí)模型基本吻合,尤其在縱向分辨率方面得到了明顯地改善.稀疏約束反演相比于平滑反演能有效地捕捉反演解的小尺度細(xì)節(jié),增強(qiáng)稀疏性以保持尖銳的邊界.模擬試算驗(yàn)證了采用模型積分靈敏度矩陣和稀疏約束算法,可以有效地消除因重力和重力梯度核函數(shù)衰減速率不同引起的趨膚效應(yīng),將該方法應(yīng)用到重力和重力梯度數(shù)據(jù)的聯(lián)合反演中可以提高縱向分辨率,降低反演多解性,獲得更加準(zhǔn)確的反演結(jié)果. 圖6 不同S矩陣的平滑和稀疏約束反演結(jié)果的對(duì)比圖(a,b,c,d) z=250 m處的橫向切片; (e,f,g,h) y=500 m處的垂向切片; (a,e) 深度加權(quán)平滑反演結(jié)果; (b,f) 深度加權(quán)稀疏約束反演結(jié)果; (c,g) 模型積分靈敏度平滑反演結(jié)果; (d,h) 模型積分靈敏度稀疏約束反演結(jié)果.Fig.6 Comparison of smooth and sparse constraint inversion results of different S matrices(a,b,c,d) In the z=250 m depth section; (e,f,g,h) In the y=500 m cross section; (a,e) The depth weighted smooth inversion results; (b,f) The depth weighted sparse inversion results; (c,g) The model integral sensitivity smooth inversion results; (d,h) The model integral sensitivity sparse inversion results. 為了證明本文提出的算法在計(jì)算時(shí)間和內(nèi)存占用量方面的優(yōu)勢(shì),我們首先設(shè)計(jì)了一個(gè)地下網(wǎng)格剖分?jǐn)?shù)量較大的簡(jiǎn)單模型,如圖7所示.模型中包含了兩個(gè)大小不同的異常體,異常體的大小分別為300 m×200 m×150 m和300 m×500 m×200 m,剩余密度均為1 g·cm-3,頂部埋深分別為150 m和200 m,相距350 m.地下模型空間尺度x,y,z為1500 m×1500 m×1000 m,將地下模型剖分為30×30×20個(gè)緊密排列的規(guī)則立方體單元,每個(gè)單元大小為50 m×50 m×50 m,背景剩余密度為0 g·cm-3.地面觀(guān)測(cè)點(diǎn)個(gè)數(shù)為30×30,觀(guān)測(cè)點(diǎn)位于網(wǎng)格中心,正演計(jì)算的觀(guān)測(cè)重力和重力梯度數(shù)據(jù)如圖7所示. 圖7 模型三的理論模型和正演響應(yīng)等值線(xiàn)圖(a) 重力gz; (b) 重力梯度分量Vxx; (c) 重力梯度分量Vxy; (d) 重力梯度分量Vzx; (e) 重力梯度分量Vzy; (f) 重力梯度分量Vzz.Fig.7 Theoretical model and forward response contour map of model 3(a) Gravity gz; (b) Gravity gradient component Vxx; (c) Gravity gradient component Vxy; (d) Gravity gradient component Vzx; (e) Gravity gradient component Vzy; (f) Gravity gradient component Vzz . 本文在改進(jìn)的共軛梯度法反演基礎(chǔ)上,分別采用模型空間和數(shù)據(jù)空間法對(duì)重力和重力梯度數(shù)據(jù)進(jìn)行聯(lián)合反演計(jì)算(計(jì)算機(jī)配置:Intel(R) Core(TM) i7-8750H CPU @ 2.20 GHz 2.21 GHz, 內(nèi)存16 GB).所有反演的初始模型均采用均勻半空間剩余密度為0 g·cm-3的模型.模型空間法反演經(jīng)過(guò)6次迭代,最終獲得的擬合差為0.99,反演結(jié)果如圖8(b,e,h)所示;數(shù)據(jù)空間法反演經(jīng)過(guò)6次迭代,最終獲得的擬合差為1.03,反演結(jié)果如圖8(c,f,i)所示.可以發(fā)現(xiàn),兩種算法得到的反演結(jié)果相似,都可以較好地恢復(fù)出異常體的邊界位置、幾何大小和物性參數(shù)值,從而證明本文提出的算法具有一定的準(zhǔn)確性.在反演計(jì)算時(shí)間方面,模型空間法耗時(shí)2061.85 s,而數(shù)據(jù)空間法耗時(shí)527.25 s,可以說(shuō)明改進(jìn)的共軛梯度法結(jié)合數(shù)據(jù)空間法有效地提高了計(jì)算效率;在內(nèi)存消耗方面,模型空間法占用的最大內(nèi)存約為12 GB,而數(shù)據(jù)空間法占用的最大內(nèi)存只需要約0.03 GB.在這個(gè)例子中,數(shù)據(jù)空間法內(nèi)存最大占用量相比于傳統(tǒng)模型空間法減小了約百分之幾. 圖8 模型空間和數(shù)據(jù)空間聯(lián)合反演結(jié)果對(duì)比圖(a,d,g) 理論模型; (b,e,h) 模型空間法反演結(jié)果; (c,f,i) 數(shù)據(jù)空間法反演結(jié)果; (a,b,c) z=300 m處的橫向切片; (d,e,f) y=750 m處的垂向切片; (g,h,i) x=1150 m處的垂向切片圖.Fig.8 Comparison of model space and data space joint inversion results(a,d,g) Theoretical model; (b,e,h) The model space inversion results; (c,f,i) The data space inversion results; (a,b,c) In the z=300 m depth section; (d,e,f) In the y=750 m cross section; (g,h,i) In the x=1150 m cross section. 為了進(jìn)一步驗(yàn)證本文提出算法的準(zhǔn)確性、抗噪性和有效性,我們又設(shè)計(jì)了一個(gè)多異常體組合復(fù)雜模型,如圖9所示,由四個(gè)不同大小的長(zhǎng)方體組成,鑲嵌在剩余密度為0 g·cm-3的地下均勻半空間中.地下模型空間大小為2000 m×2000 m×1000 m,將地下剖分為40×40 ×20個(gè)緊密排列的直立立方體單元,每個(gè)單元大小為50 m×50 m×50 m.地面觀(guān)測(cè)點(diǎn)個(gè)數(shù)為40×40,觀(guān)測(cè)點(diǎn)位于網(wǎng)格中心,加入5%高斯隨機(jī)噪聲的理論模型正演響應(yīng)如圖9所示.異常體的物性值、幾何大小和頂部埋深情況如表2所示. 圖9 模型四的理論模型和正演響應(yīng)等值線(xiàn)圖(a) 重力gz; (b) 重力梯度分量Vxx; (c) 重力梯度分量Vxy; (d) 重力梯度分量Vzx; (e) 重力梯度分量Vzy; (f) 重力梯度分量Vzz.Fig.9 Theoretical model and forward response contour map of model 4(a) Gravity gz; (b) Gravity gradient component Vxx; (c) Gravity gradient component Vxy; (d) Gravity gradient component Vzx; (e) Gravity gradient component Vzy; (f) Gravity gradient component Vzz. 表2 理論模型異常體屬性情況Table 2 Theoretical model anomaly attributes 由于網(wǎng)格剖分個(gè)數(shù)的增加,采用模型空間法進(jìn)行反演計(jì)算所需要的內(nèi)存空間已經(jīng)超過(guò)計(jì)算機(jī)的承受范圍,而數(shù)據(jù)空間法反演經(jīng)過(guò)17次迭代,最終獲得的擬合差為0.97,反演結(jié)果如圖10所示.可以發(fā)現(xiàn),加入噪聲后本文提出的算法仍然能夠準(zhǔn)確地恢復(fù)出地下異常體的幾何形態(tài)和物性參數(shù)值大小,與真實(shí)模型基本吻合,表現(xiàn)出一定的準(zhǔn)確性和抗噪性.反演計(jì)算耗時(shí)2206.26 s,占用的最大內(nèi)存約為0.039 GB.在這個(gè)例子中,數(shù)據(jù)空間法反演內(nèi)存最大占用量相比于傳統(tǒng)模型空間法減小了約百分之幾,可以證明改進(jìn)的共軛梯度法結(jié)合數(shù)據(jù)空間法有效地降低了計(jì)算內(nèi)存消耗量,表現(xiàn)出一定的有效性,更適合應(yīng)用于大數(shù)據(jù)量的重力和重力梯度數(shù)據(jù)聯(lián)合反演計(jì)算. 圖10 數(shù)據(jù)空間共軛梯度法聯(lián)合反演結(jié)果圖(a,b,c,d) 理論模型; (e,f,g,h) 聯(lián)合反演結(jié)果; (a,e) z=300 m處的橫向切片; (b,f) x=600 m處的垂向切片; (c,g) y=550 m處的垂向切片; (d,h) x=1600 m處的垂向切片.Fig.10 The data space conjugate gradient method joint inversion results(a,b,c,d) Theoretical model; (e,f,g,h) Joint inversion results; (a,e) In the z=300 m depth section; (b,f) In the x=600 m cross section; (c,g) In the y=550 m cross section; (d,h) In the x=1600 m cross section. 為了進(jìn)一步說(shuō)明本文提出算法的有效性和實(shí)用性,我們將反演算法應(yīng)用于黑龍江省大興安嶺呼中區(qū)碧水鎮(zhèn)鉛鋅多金屬礦區(qū)的重力和重力梯度數(shù)據(jù)解釋中.在碧水鎮(zhèn)鉛鋅多金屬礦區(qū)內(nèi)共采集了27條測(cè)線(xiàn),測(cè)線(xiàn)間距40 m,每條測(cè)線(xiàn)上分布16個(gè)觀(guān)測(cè)點(diǎn),測(cè)點(diǎn)間距40 m,將實(shí)測(cè)布格剩余重力異常數(shù)據(jù)網(wǎng)格化,網(wǎng)格化后的重力異常數(shù)據(jù)等值線(xiàn)如圖11a所示.利用傅里葉變換計(jì)算得到布格剩余重力異常的重力梯度數(shù)據(jù),網(wǎng)格化后的重力梯度異常數(shù)據(jù)如圖11b所示.方便起見(jiàn),實(shí)測(cè)數(shù)據(jù)應(yīng)用中只考慮重力和重力梯度Vzz分量數(shù)據(jù)進(jìn)行聯(lián)合反演計(jì)算. 圖11 實(shí)測(cè)重力和重力梯度數(shù)據(jù)等值線(xiàn)圖(a) 重力數(shù)據(jù); (b) 重力梯度數(shù)據(jù)Vzz.Fig.11 Contour plots of measured gravity and gravity gradient data(a) The gravity data; (b)The gravity gradient data Vzz. 觀(guān)測(cè)區(qū)域大小為640 m×1040 m,將反演目標(biāo)區(qū)域的地下空間劃分為16×27×10個(gè)緊密排列的直立長(zhǎng)方體單元,每個(gè)單元的大小為 40 m×40 m×40 m.我們對(duì)重力和重力梯度數(shù)據(jù)進(jìn)行聯(lián)合反演,反演初始模型采用剩余密度為0 g·cm-3的均勻半空間模型.反演經(jīng)過(guò)5次迭代收斂到擬合差閾值以下,反演結(jié)果沿測(cè)線(xiàn)方向的密度分布切片如圖12所示,不同深度的密度分布切片如圖13所示.我們發(fā)現(xiàn),本文提出的反演方法可以快速地分辨出地下不同密度的分布情況,密度異常分布從南到北逐漸升高,高密度異常區(qū)域主要出現(xiàn)在研究區(qū)的東北方向,由于鉛鋅多金屬礦床具有較高的密度,因此可以通過(guò)反演高密度分布情況有效地圈定多金屬礦床的區(qū)域位置和劃分礦體與圍巖的邊界.同時(shí),該反演算法獲得最終模型結(jié)果耗時(shí)約434.5 s,占用內(nèi)存約0.028 GB.進(jìn)一步說(shuō)明了所提出的算法適用于實(shí)測(cè)數(shù)據(jù)處理,可以在普通計(jì)算機(jī)下快速獲得地下密度分布模型,為精準(zhǔn)礦產(chǎn)勘探提供重要依據(jù). 圖12 重力和重力梯度數(shù)據(jù)聯(lián)合反演獲得的密度分布垂向切片圖Fig.12 Cross section of density distribution obtained by joint inversion of gravity and gravity gradient data 圖13 重力和重力梯度數(shù)據(jù)聯(lián)合反演獲得的密度分布橫向切片圖(a) z=100 m處的橫向切片; (b) z=200 m處的橫向切片; (c) z=300 m處的橫向切片.Fig.13 Depth section of density distribution obtained by joint inversion of gravity and gravity gradient data(a) In the z=100 m depth section; (b) In the z=200 m depth section; (c) In the z=300 m depth section. 本文將數(shù)據(jù)空間法和改進(jìn)的共軛梯度算法結(jié)合應(yīng)用到重力和重力梯度數(shù)據(jù)處理中,開(kāi)發(fā)出計(jì)算速度更快、占用內(nèi)存更小的高分辨率三維重力和重力梯度數(shù)據(jù)聯(lián)合反演算法.理論模型試算表明相比于傳統(tǒng)的共軛梯度反演算法,改進(jìn)的算法可以有效地降低反演的迭代次數(shù),提高反演的收斂速度,獲得更接近于真實(shí)模型的反演結(jié)果;聯(lián)合反演采用自適應(yīng)模型積分靈敏度矩陣,可以有效地消除因重力和重力梯度核函數(shù)衰減速率不同引起的趨膚效應(yīng),相比于依賴(lài)先驗(yàn)信息的深度加權(quán)方法,可以自適應(yīng)調(diào)解矩陣大小,有效提高反演結(jié)果的縱向分辨率;稀疏約束反演方法相比于傳統(tǒng)平滑反演方法能有效地捕捉反演解的小尺度細(xì)節(jié),增強(qiáng)稀疏性以保持尖銳的邊界;將數(shù)據(jù)空間法和改進(jìn)的共軛梯度算法結(jié)合,可以更好地降低聯(lián)合反演求解方程的維度,避免存儲(chǔ)靈敏度矩陣,有效地提高了計(jì)算效率和大幅度的降低內(nèi)存占用空間.野外實(shí)例表明,本文提出的算法可以在普通計(jì)算機(jī)下快速地獲得地下密度分布模型,有效地圈定多金屬礦床的區(qū)域位置和劃分礦體與圍巖的邊界,表現(xiàn)出較強(qiáng)的穩(wěn)定性和實(shí)用性. 致謝感謝匿名評(píng)審專(zhuān)家為本文提出的寶貴意見(jiàn).
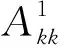
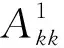
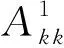
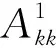
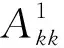
2 反演計(jì)算理論
2.1 目標(biāo)函數(shù)
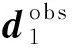
2.2 目標(biāo)函數(shù)的優(yōu)化
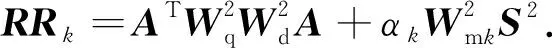
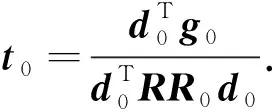
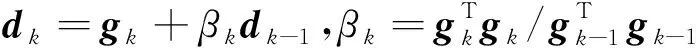
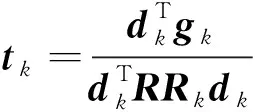
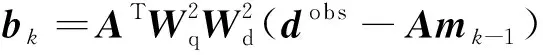
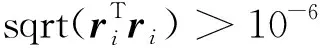
2.3 數(shù)據(jù)空間共軛梯度法
3 模型試算
3.1 單獨(dú)和聯(lián)合反演對(duì)比

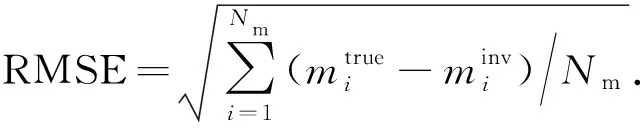
3.2 傳統(tǒng)和改進(jìn)的共軛梯度法反演對(duì)比
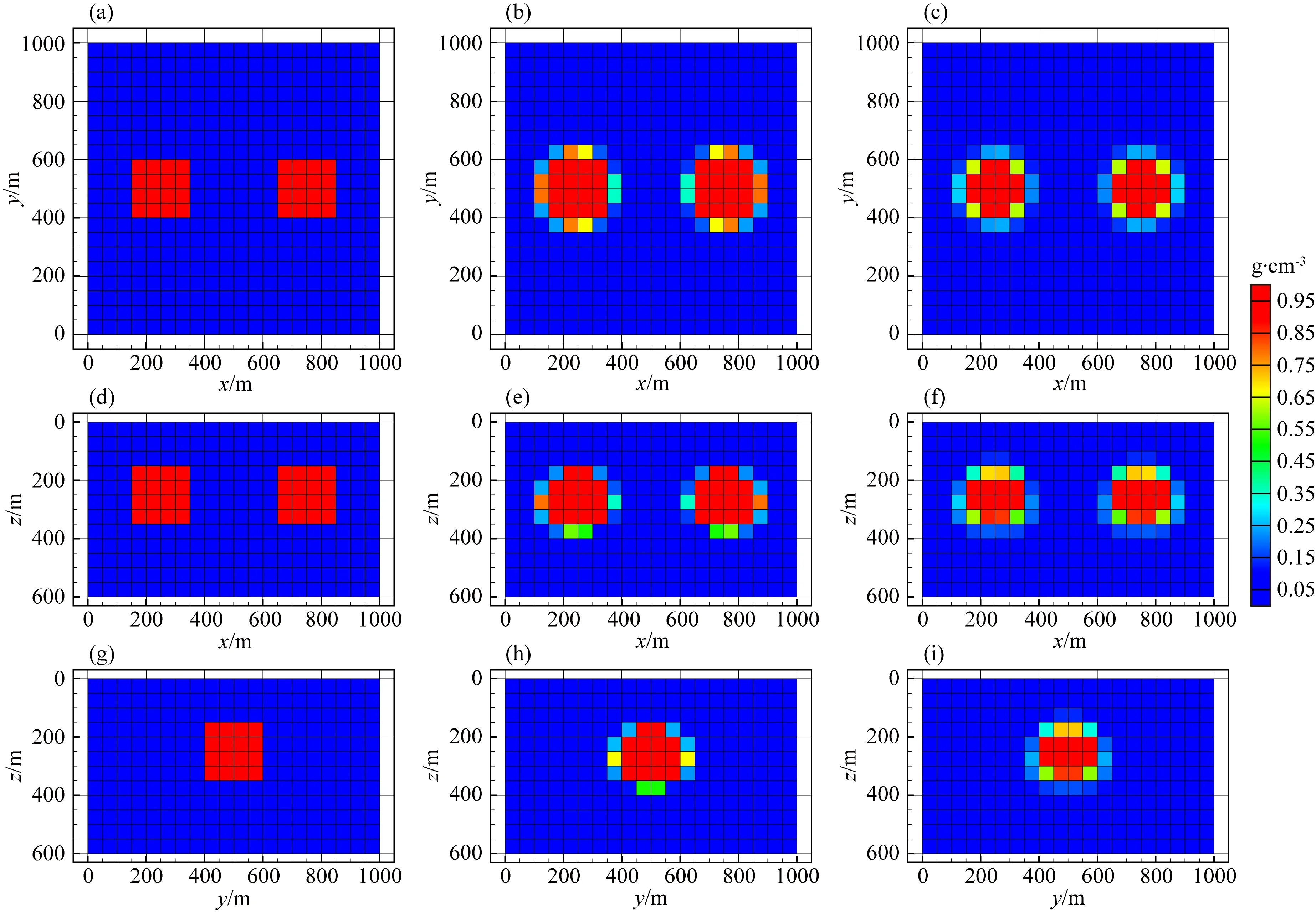
3.3 模型積分靈敏度矩陣和深度加權(quán)矩陣對(duì)比
3.4 模型空間和數(shù)據(jù)空間法對(duì)比


4 實(shí)測(cè)數(shù)據(jù)應(yīng)用
5 結(jié)論
