橫梁端部節點優化

呂忠杰，王 樂，朱永安

(江南造船(集團)有限責任公司，上海 201913)

0 引 言

橫梁(含縱桁和豎桁)是船舶結構的重要組成部分，由腹板面板焊接而成，主要起保證甲板強度和力的傳遞作用[1]。

不同的端部連接形式對結構整體強度、鋼材使用量、艙室空間利用率、施工便利性等方面都有著不同的影響。選取船體不同典型部位橫梁端部節點，設計3種不同類型的節點形式。建立基于精細網格的計算機輔助工程(Computer Aided Engineering，CAE)有限元模型，計算分析典型節點的應力分布規律。比較分析不同連接形式的優缺點，提出針對指定部位較優的T型材端部連接節點的形式和尺寸[2]。

根據橫梁的受力特點，選取主船體甲板橫梁端部與舷側肋骨/主縱艙壁豎桁的相交節點，分別以肘板連接、趾端增大和圓弧連接等3種連接方式作為強構件間的過渡形式，建立不同連接類型的三維有限元模型，進行強度分析計算，重點對不同節點形式連接區域構件的趾端位置單元的應力水平及分布規律進行對比、分析和探討。根據對比分析得到的結果，確定較優的連接過渡方式及過渡結構的參數尺寸。

1 研究對象選取

1.1 概 述

甲板橫梁端部節點形式通常有三角形肘板+面板結構(其中肘板寬度是T型材腹板高度的1.20～1.43倍)、橫梁端部趾端增大和橫梁端部圓弧連接等3種，通過變換圓弧連接節點的主要參數，進行基于精細網格的CAE有限元比較分析計算，優化得到相對較優的橫梁端部連接節點形式,如圖1所示。

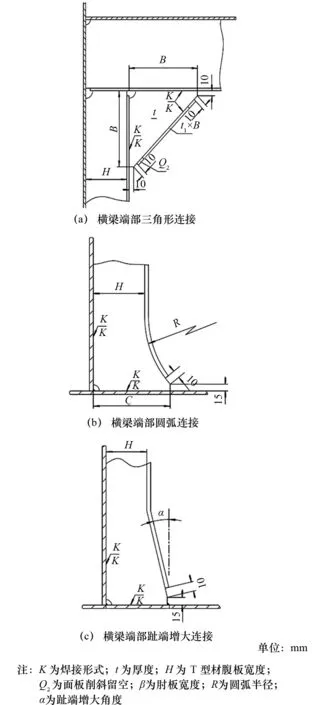
圖1 橫梁端部3種連接節點形式

1.2 節點選取

選取典型部位(甲板橫梁端部與舷側肋骨/主縱艙壁豎桁相交節點)，以下簡稱“典型部位模型”，如圖2所示，進行節點強度計算。

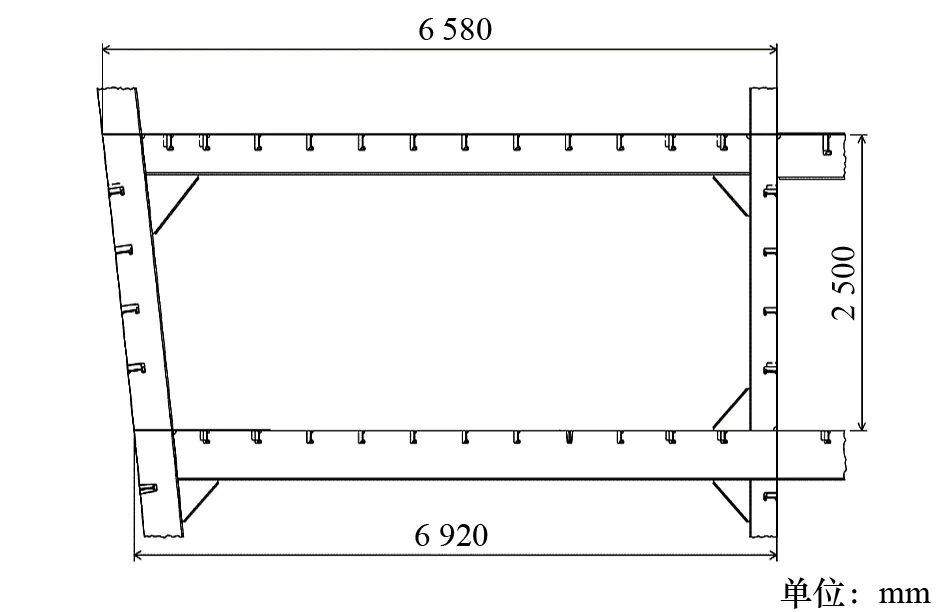
圖2 典型部位模型結構尺寸

典型部位的橫梁端部連接方式包含3種連接節點形式，分別為連接形式1、2、3，對應圖1中(a)、(b)、(c)。3種節點的連接方式相關參數尺寸設置如圖1所示。其中，節點的參數尺寸包括：采用三角肘板連接時肘板的寬度B；采用圓弧連接方式時的圓弧半徑R；圓弧端部高度C；采用趾端增大角度α的連接方式。

根據布置的具體需求，如B、C過大則不利于艙室布置； 如R過大則橫梁端部過渡區域增大，耗費鋼材。

綜合考慮上述因素，并參考以往船舶的橫梁端部節點形式，對主要參數尺寸進行變換組合，如表1所示。

表1 不同連接方式橫梁端部節點主要尺寸

2 計算模型

通過改變連接過渡方式及參數尺寸分別構造5個節點模型，計算分析其應力情況。模型尺寸及參數如表2所示。

表2 5個節點模型尺寸及參數

2.1 模型范圍及網格

CAE網格的劃分中，對非細化區域內的網格劃分為100 mm×100 mm，細化區域的網格大小為10 mm×10 mm[3]。

模型范圍。船長方向：由細化節點肋位分別向艏艉延伸至相鄰強框架；船寬方向：甲板由主縱艙壁向船中延伸4個縱骨間距；垂向：舷側板和主縱艙壁由細化區域向上延伸至相鄰甲板，向下延伸至相鄰第2層甲板。

模型存在2個細化區域，如圖3框示位置。

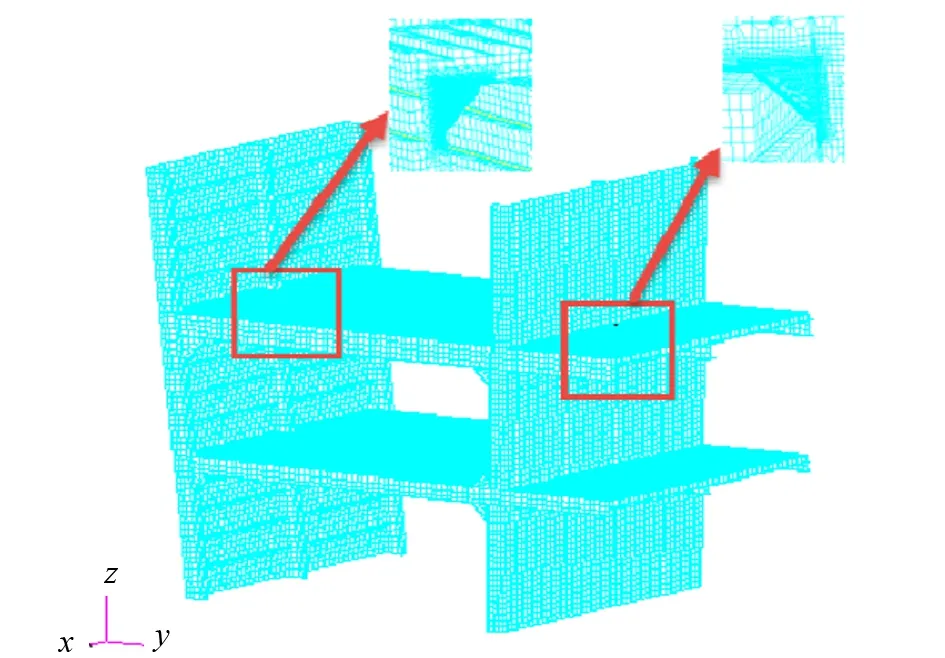
圖3 模型范圍

在3種連接方式下細化區域的網格劃分情況如圖4所示。

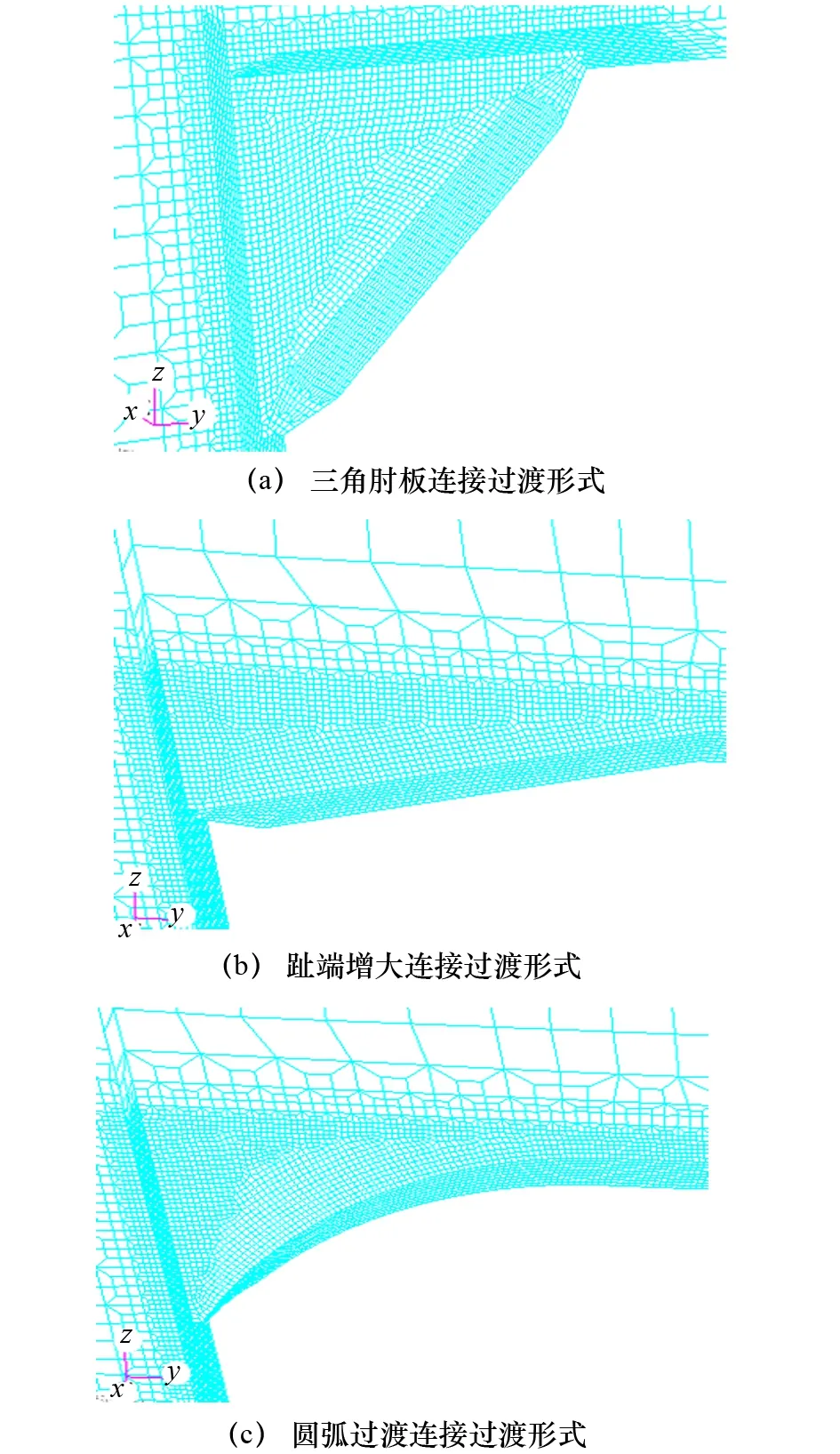
圖4 在3種連接形式下細化網格劃分情況

模型中的甲板板、外板板、艙壁、甲板橫梁、實肋板、豎桁的腹板均采用板單元模擬，對于細化區域的強橫梁、豎桁的面板也采用板單元模擬。

模型中主要采用四邊形單元，采用少量三角形網格過渡，四邊形單元的邊長比控制在1∶2以內。

節點模型1～節點模型3中非細化區域的強橫梁、水平桁、豎桁的面板，模型中的縱骨、加強筋均采用梁單元模擬。模型中的板厚云圖如圖5所示。

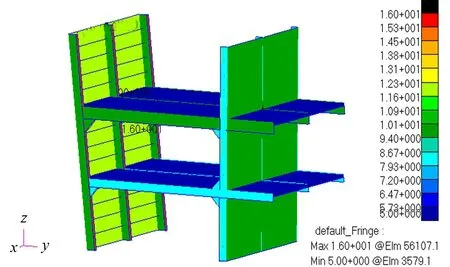
圖5 模型厚度云圖

2.2 節點質量對比

3種節點連接形式甲板橫梁與舷側豎桁的相交節點處的質量與采用三角肘板連接時的節點質量進行對比，其中，采用三角肘板的質量最大，其他連接方式與其差距如表3所示。

統計結果，若全船T型材肘板(三角形)數量按約1萬個計算，如果橫梁端部采用圓弧連接或趾端增大連接，每個連接節點平均質量減輕按10 kg計算，那么全船由此可以減輕質量約100 t。

表3 典型部位在不同節點模型工況下的質量差

2.3 載 荷

對典形部位模型橫梁所在甲板施加均布載荷，載荷大小為0.01 MPa(1 m水柱，如圖6所示)，使甲板橫梁受彎，考察甲板橫梁端部與舷側肋骨或主縱艙壁豎桁相交節點的應力水平。

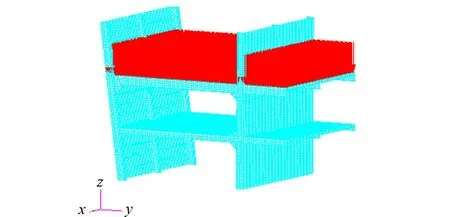
圖6 模型載荷示例

2.4 邊界條件

3種不同的節點模型的約束條件與其在整船中的相對位置和受力情況相關。為盡量模擬真實，根據3種節點模型在整船中真實的受力情況和邊界條件，對模型施加不同約束，邊界條件如表4所示。

表4 邊界條件

節點模型的邊界約束位置如圖7所示。

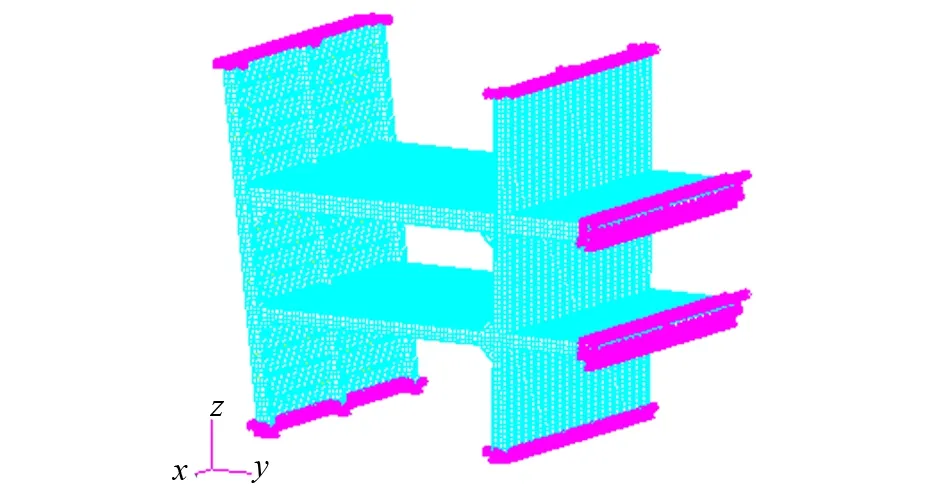
圖7 模型邊界條件

3 應力計算結果及對比分析

3.1 節點模型應力云圖

由于重點考察典型節點強度性能，且細化節點外結構應力普遍偏小，為使應力云圖更加直觀鮮明，截取5種節點模型單元形心處中面von Mises應力云圖及軟趾應力分布放大圖，如圖8～圖12所示。

圖8 節點模型1單元形心處中面von Mises應力云圖及軟趾應力分布放大圖

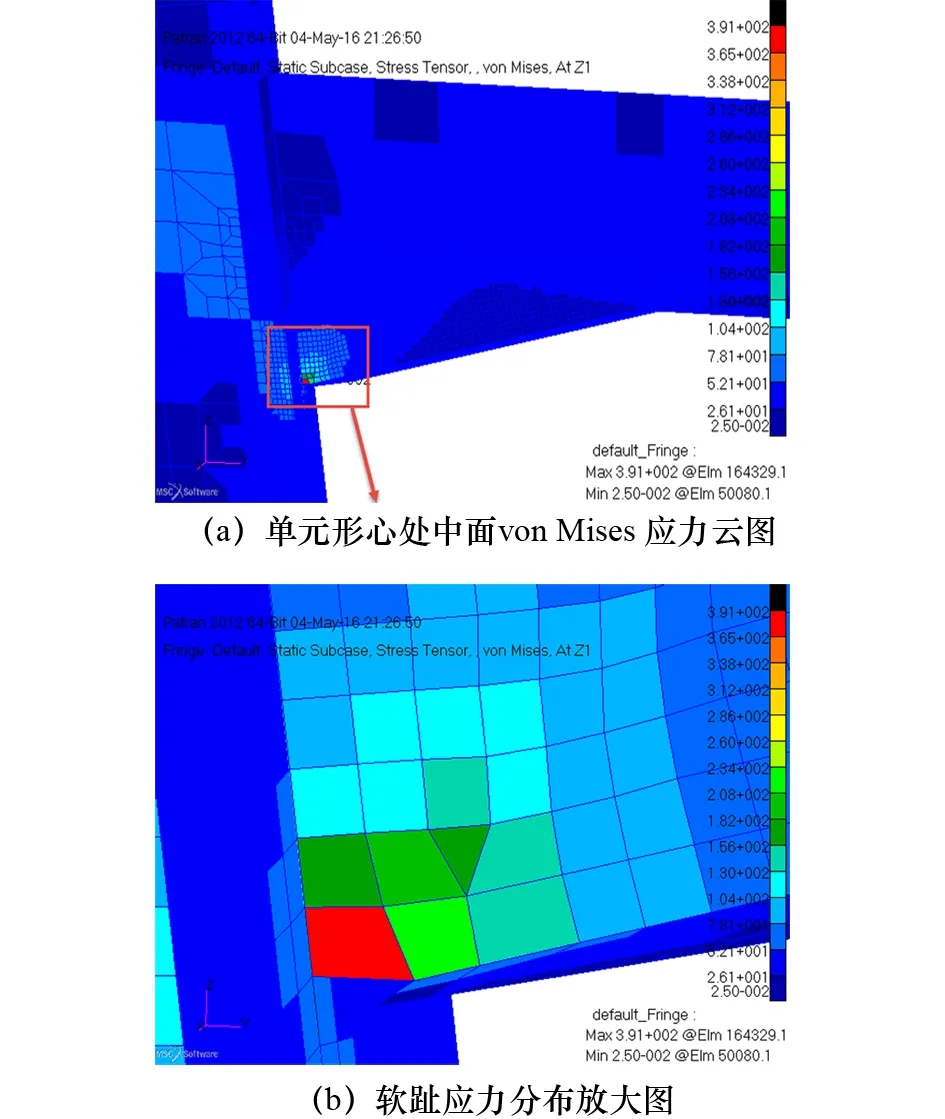
圖9 節點模型2單元形心處中面von Mises應力云圖及軟趾應力分布放大圖

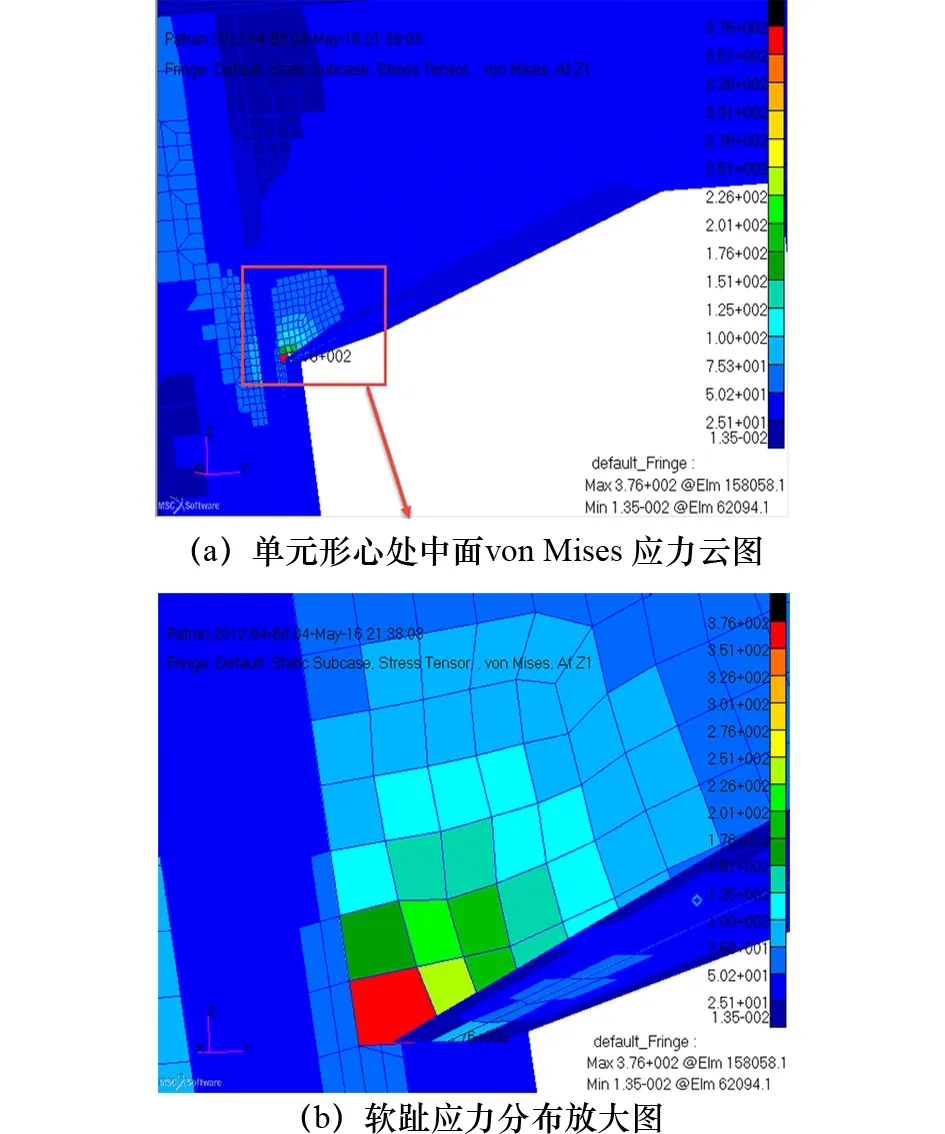
圖10 節點模型3單元形心處中面von Mises應力云圖及軟趾應力分布放大圖

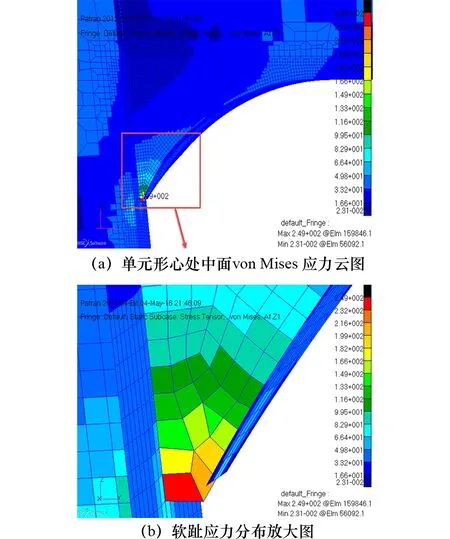
圖11 節點模型4單元形心處中面von Mises應力云圖及軟趾應力分布放大圖

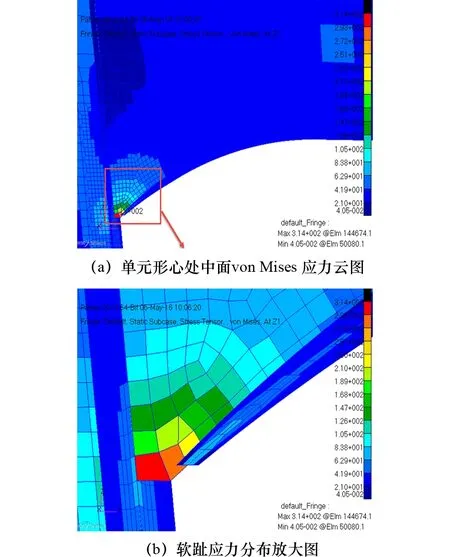
圖12 節點模型5單元形心處中面von Mises應力云圖及軟趾應力分布放大圖

圖8為節點模型1，顯示軟趾應力峰值單元中面應力為276 MPa。

圖9為節點模型2，顯示軟趾應力峰值單元中面應力為391 MPa。

圖10為節點模型3，顯示軟趾應力峰值單元中面應力為376 MPa。節點模型3，即在趾端處增大角度α=20°，軟趾應力峰值單元中面應力相對較小。

圖11為節點模型4，顯示軟趾應力峰值單元中面應力為249 MPa。節點模型4，即采用圓弧過渡B=2H、R=2H時，軟趾應力峰值單元中面應力相對較小。

圖12為節點模型5，顯示軟趾應力峰值單元中面應力為314 MPa。

3.2 結果與對比分析

由上述應力云圖可看出：5個不同連接過渡方式的應力峰值基本都出現在同一位置的單元上。

節點模型中應力峰值均出現在甲板橫梁與舷側豎桁的相交節點處，其中采用圓弧過渡B=2H、R=2H時，軟趾應力峰值單元中面應力最小為249 MPa。

在典型節點性能數值計算中，使用三角肘板連接時由于結構中加載方式的單一性，且三角肘板存在2個軟趾區域，使得三角肘板中應力峰值出現的位置往往與采用其他連接方式有差異，為使應力結果具有可對比性，對5個不同節點模型對比同一相對位置軟趾處單元的應力峰值。

除節點處的應力峰值單元外，當各節點模型采用不同連接方式和參數尺寸時，橫梁跨中應力峰值如表5所示。

表5 不同節點模型跨中應力峰值

由表5可看出：采用不同的連接方式和參數尺寸時跨中的應力變化不大，即典型節點采用不同的連接方式和參數尺寸時，僅對節點性能有較大影響。

4 結 論

通過計算分析可得到如下結論：

(1) 通過典型節點性能的數值計算，可在三角肘板、圓弧過渡及趾端增大等3種連接方式中找到T型材端部節點較優的連接過渡方式與較優的設計尺寸。綜合考慮，得到典型節點處較優的連接方式為節點模型4，即圓弧過渡B=2H、R=2H。

(2) 采用三角肘板連接過渡時，可在節點處形成局部框架，對局部有加強作用，相對于圓弧連接和趾端增大的連接方式，對節點處應力的整體水平有降低的效果，采用三角肘板連接時，工藝要求低，建造容易。但由于三角肘板在軟趾處形成應力集中，該處的應力相對于采用圓弧過渡和趾端增大的連接方式要大得多，且采用三角肘板鋼料質量會較大。而采用圓弧過渡和趾端增大的連接方式時，由于面板的連續性較好，有利于降低節點處的峰值應力，可延長節點構件的使用壽命。