網絡攻擊下的Markov跳變系統有限時間控制

譚 天 高金鳳 王錦霞 汪家琪

(浙江理工大學機械與自動控制學院 杭州 310018)

(tantian5991@163.com)

隨著信息技術和工業水平的飛速發展,網絡控制系統的研究與應用愈發廣泛,傳統的“點對點”式控制系統由于其無法滿足當前控制對象的遠距離、多分布、可監控、數據傳輸共享的高效率以及網絡安全等需求而逐漸被放棄.網絡控制系統具有高效的數據通信與共享、安裝與維護靈活、集散遠程控制等優點,成為當前網絡控制系統領域的研究熱點[1-2].

網絡控制系統(networked control systems, NCSs)是由傳感器、控制器、執行器、被控對象以及共享通信網絡構成的閉環系統.當前針對NCSs的研究主要問題在于：一方面由于大量的被控對象使用同一通信網絡,不可避免地存在網絡時延、數據丟包等影響系統性能的問題;另一方面,大量的工業系統追求控制性能和生產效率而忽略了網絡系統的安全問題,NCSs一旦遭受網絡黑客攻擊,極大程度上將造成重大經濟損失[3-6].此外,目前大多數工業系統僅在無限時域內維持系統的穩定性,但是關于系統在短時間內穩定的暫態性能的研究,如電力網絡、機器人精微控制等仍然較少,有待發展.

Markov跳變系統是一種特殊的隨機系統,相應的系統模態由Markov過程進行描述.不同模態之間的切換即是Markov跳變過程,也稱作Markov鏈.系統的參數由于會受到外界因素的干擾而發生隨機跳變,因此,實際生產生活中的許多對象都可以抽象為Markov跳變系統.對于Markov跳變系統的研究也因此具有理論意義與實際意義[7-11].

基于上述關于Markov跳變系統和網絡攻擊的問題,有許多學者發表了極具價值的研究文章.干珊珊等人[7]基于雙邊時延和丟包的Markov跳變系統,研究了其有限時間控制；Liu等人[12]對遭遇隨機網絡攻擊的T-S模糊NCSs,研究了其量化穩定性質；Tan等人[8]對不確定Markov跳變系統在無限時間域內的混雜驅動機制進行了研究；Gao等人[9]在離散時間非齊次Markov跳變系統的基礎上,設計了相關的有限時間觀測器,并將推導的結論應用到在直流電動機中進行仿真,證明了推導定理的有效性；Zha等人[10]在Markov跳變系統的基礎上,研究了事件觸發機制和量化對公共信號傳輸網絡的優化問題,通過減少無效信號的傳輸以降低通信負擔；Ren等人[11]對正定Markov跳變神經網絡在有限時間內的穩定性進行了研究；Wu等人[13]在NCSs遭受欺騙攻擊的情況下,設計了相關的有限時間事件觸發濾波器,并通過仿真驗證了其定理的合理性和有效性；Shen等人[14]對于T-S模糊Markov跳變系統,研究了其有限時間事件觸發的H∞控制,并通過實際應用例子仿真說明了系統在有限時間內穩定.

綜上所述,本文研究了在遭受網絡攻擊情況下,Markov跳變系統的輸出反饋有限時間H∞控制,其中為了降低無效數據的傳輸量,降低網絡通信帶寬負擔,提升系統性能,采用了混雜驅動機制和雙通道量化.本文的主要工作包含以下幾個方面:1)建立輸出反饋Markov跳變系統的數學模型,引入混雜驅動機制和雙通道量化,減少數據傳輸率,提高系統性能;2)引入網絡攻擊模型模擬系統遭受外部攻擊,在此情況下系統依然保持穩定的狀態;3)根據有限時間定義和H∞范數有界定義,證明了系統在漸近穩定的情況下能夠保持有限時間穩定且滿足H∞性能指標.

1 問題描述與系統建模

1.1 系統描述

考慮如下所示的Markov跳變系統:

(1)

其中,?(t),y(t),z(t)分別表示狀態向量、測量輸出與控制輸入；u(t)表示控制輸出；N(t)表示注入系統的外部擾動信號.它們均滿足:?(t)∈m,y(t)∈n,z(t)∈p,N(t)∈q,其中且滿足

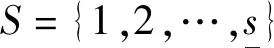
其中,λij表示從模態i跳變到模態j的轉移概率.

為方便表示,令rt=i,則Art,Brt,Crt,Drt,Ert,Frt分別由Ai,Bi,Ci,Di,Ei,Fi替代.

為研究本文所涉及的系統的穩定性,我們定義如下輸出反饋控制器:

u(t)=Kiy(tkh),

(2)

其中,t∈[tkh+τtk,tk+1h+τtk+1),i∈S,Ki表示系統處于不同模態時控制器的增益,τtk表示傳感器到控制器、控制器到執行器的時延,也即系統時延.

1.2 混雜驅動機制

對于網絡控制系統,在保證系統通信質量良好、維護系統穩定性的前提下,盡可能地減少“無效信號”的傳輸與發送,以節省網絡帶寬資源和降低網絡通信負擔.基于文獻[15],我們利用混雜驅動機制以處理信號傳輸問題.

1.2.1 時間觸發機制

傳感器在固定時間進行數據采集的模式,稱為時間觸發機制.定義系統時延?(t)=t-tkh,其中t∈[tkh+τtk,tk+1h+τtk+1),此時,相應的控制器為

u1(t)=Kiy(t-?(t))=KiDi?(t-?(t)),

(3)

其中0≤?(t)≤?m,?m表示系統時延的上界.

1.2.2 事件觸發機制

為解決時間觸發機制數據冗余的弊端,文獻[16]提出了一種新的數據采集方式,即事件觸發機制.混雜驅動機制是由伯努利分布將時間觸發與事件觸發進行統一.與時間觸發的固定周期數據采樣方式不同,傳感器采集的信號要進行傳輸,其需要滿足以下條件[17]:

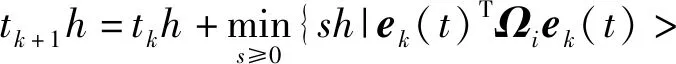
(4)

其中,ek(t)=?(tkh)-?(tkh+sh),且s為非負整數,數據傳輸時間的區間為[tkh,tk+1h),Ω為正定對稱加權矩陣,且δ∈[0,1].

根據文獻[18],將Markov跳變系統建模為等價的時滯系統,其相應的輸出反饋事件觸發條件變為

(5)

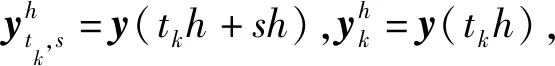
?(tkh)=?(t-τ(t))+ek(t),

(6)

根據式(2)和式(6),相應的系統控制器為

u2(t)=Kiy(tkh)=KiDi?(tkh)=
KiDi[?(t-τ(t))+ek(t)],

(7)

根據系統模型式(1)與事件觸發條件式(5),在本文研究的系統中,當違背以下事件觸發條件時,采樣信號才得以傳輸:

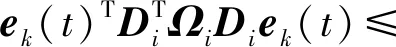
(8)

綜上,基于文獻[15]可以得到基于混雜驅動機制的控制器:

u?(t)=α(t)u1(t)+(1-α(t))u2(t)=
α(t)KiDi?(t-?(t))+(1-α(t))×
KiDi[?(t-τ(t))+ek(t)],

(9)

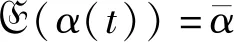
1.3 量 化

在當前網絡控制系統中,面對大量的分散數據采集點發送數據的情況,傳輸所有的數據顯得不現實.有學者提出了量化技術[19],將連續信號離散化,從而在通信時僅傳輸少量量化后的數據,降低了網絡通道負擔.根據文獻[20],定義量化器h(y)=[h1(y1)h2(y2)h3(y3)…hn(yn)]T,設置于傳感器端,其中,hi(yi)為

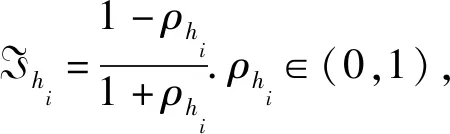
h(x)=(I+Δh)x.

(10)

同理,類似于h(y),另一側通道的量化器可表示為

g(x)=(I+Δg)x.

(11)

綜上所述, 在混雜驅動機制的基礎上,考慮雙通道的量化器,有如下控制器:

uqs(t)=α(t)Ki(I+Δh)(I+Δg)Di?(t-?(t))+
(1-α(t))Ki(I+Δh)(I+Δg)Di[?(t-τ(t))+
ek(t)]=α(t)(Ki+ΔKi)Di?(t-?(t))+
(1-α(t))(Ki+ΔKi)Di[?(t-τ(t))+ek(t)],

(12)

其中ΔKi=ΔgKi+KiΔh+ΔgKiΔh.

1.4 欺騙攻擊

在通信網絡中,由于網絡安全的缺失,使得網絡系統在傳輸數據的過程中極易遭遇來自外界的攻擊,欺騙攻擊屬于其中的一種攻擊方式.攻擊者通過向公共網絡通道中注入欺騙信號,達到干擾正常信號傳輸的目的,造成系統的失穩甚至崩潰.為了處理這樣的問題,文獻[22]提出了一種方式,將欺騙攻擊建模為如下形式:

(13)

其中H為常系數矩陣,表示攻擊上限.

忽略欺騙攻擊的時延,在控制器側有

(14)

在該Markov跳變系統中,若欺騙攻擊事件發生在傳感器采樣輸出之前,根據式(13)(14),有

u(t)=uqs(t)+β(t)[KiDiξ(t)-uqs(t)].

(15)

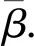
根據式(12)～(14),系統的輸出反饋控制器可以改寫為

u(t)=(1-β(t))α(t)(Ki+ΔKi)Di?(t-?(t))+
(1-β(t))(1-α(t))(Ki+ΔKi)Di[?(t-τ(t))+
ek(t)]+β(t)KiDiξ(t).

(16)

綜上所述,本文中基于混雜驅動機制的Markov跳變連續系統可定義為

(17)

為方便穩定性定理的證明,下面給出相關的定義與引理.

定義1[23].給定正標量參數和正定矩陣(ε1,ε2,R,d)及時間區間t∈[0,T],其中T>0,0<ε1<ε2.Markov跳變系統式(17)是有限時間有界的,如果以下條件成立:

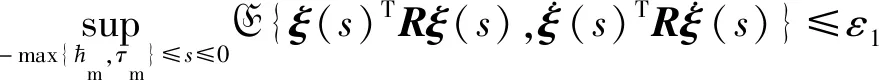
定義2[24].在定義1的基礎上,當系統處于零初始條件,Markov跳變系統式(17)滿足參數γ>0的有限時間H∞性能水平,即

引理1[25].若存在τ(t)>0且屬于[τlest,τhest]和適維矩陣Mi(i=1,2,3),如下不等式成立:

(τ(t)-τlest)M1+(τhest-τ(t))M2+M3<0,

且等價于

(τhest-τlest)M1+M3<0,(τhest-τlest)M2+M3<0.

2 主要結果

在本節中,針對基于混雜驅動機制和量化的Markov跳變系統,在遭遇欺騙攻擊的情況下,推導了該系統在有限時間內的H∞穩定性定理.

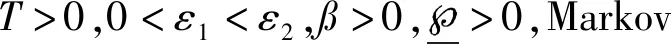
(18)

(19)

其中

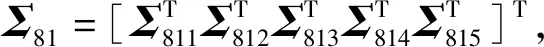
證明. 針對閉環Markov跳變系統式(17),考慮構建如下Lyapunov-Krasovskii泛函:

V(t)=V1(t)+V2(t)+V3(t)，

(20)

其中

V1(t)=?(t)TPi?(t)，

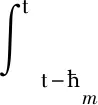
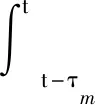
求取泛函式(20)的導數及期望:

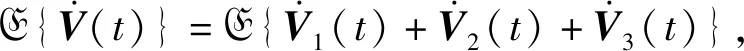
令

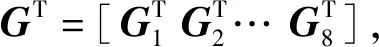
根據自由權矩陣方法及引理1:

以上是在無限時間內系統的穩定性證明,下面考慮在有限時間內系統的穩定性.

由式(18)可知:

(21)

對式(21)左右同乘以?e-?t,并根據Newton-Leibniz公式從0到T進行積分,可以得到:

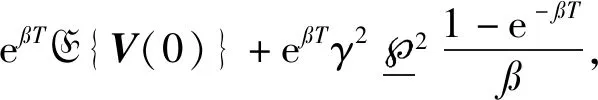
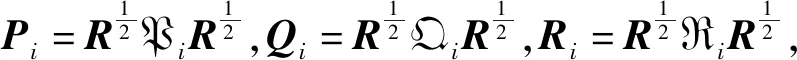
E{V(0)}≤λ?ε1,

其中

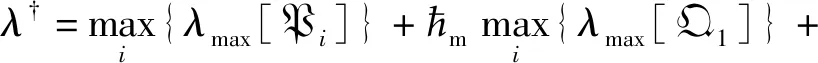
另外

E{?(t)TPi?(t)}≥λmin[Pi]E{?(t)TRi?(t)}.

由此,式(19)成立,即Markov跳變系統式(17)是有限時間有界的.針對系統式(17)的H∞性能,有

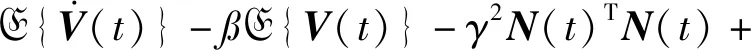
對等式左右同乘e-?t,并在零初始條件下對其在0到T進行積分,可以得到

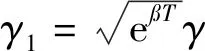
證畢.

3 數值仿真

為說明本文所提出的定理的有效性,本節將給出2個仿真實例進行驗證說明.

例1.考慮如下系統參數.

模態1:

模態2:

混雜驅動桿狀圖如圖1所示,狀態響應曲線如圖2所示.

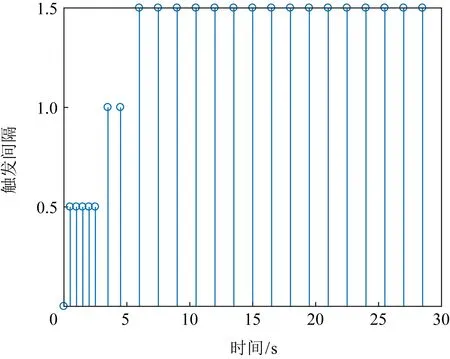
圖1 觸發桿狀圖(例1)

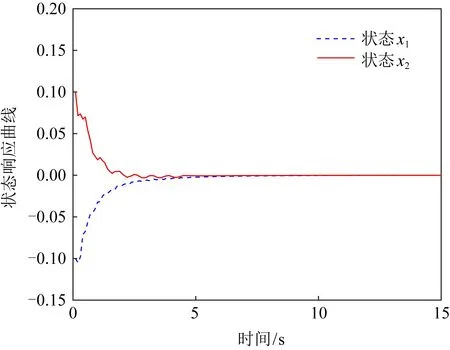
圖2 狀態響應曲線(例1)

由圖1可知,在混雜驅動狀態下,數據的傳輸量為24,即在采樣周期為0.1的情況下,30 s內的數據傳輸率為8%,且系統在有限的時間內能夠趨于漸進穩定.此外,在系統中設計的攻擊信號函數,模擬了控制系統在遭遇網絡攻擊的情況,系統依然能夠在有限時間內恢復穩定,表明了本文提出并推導的定理的有效性.

例2.考慮風光微電網直流發電系統如圖3所示:

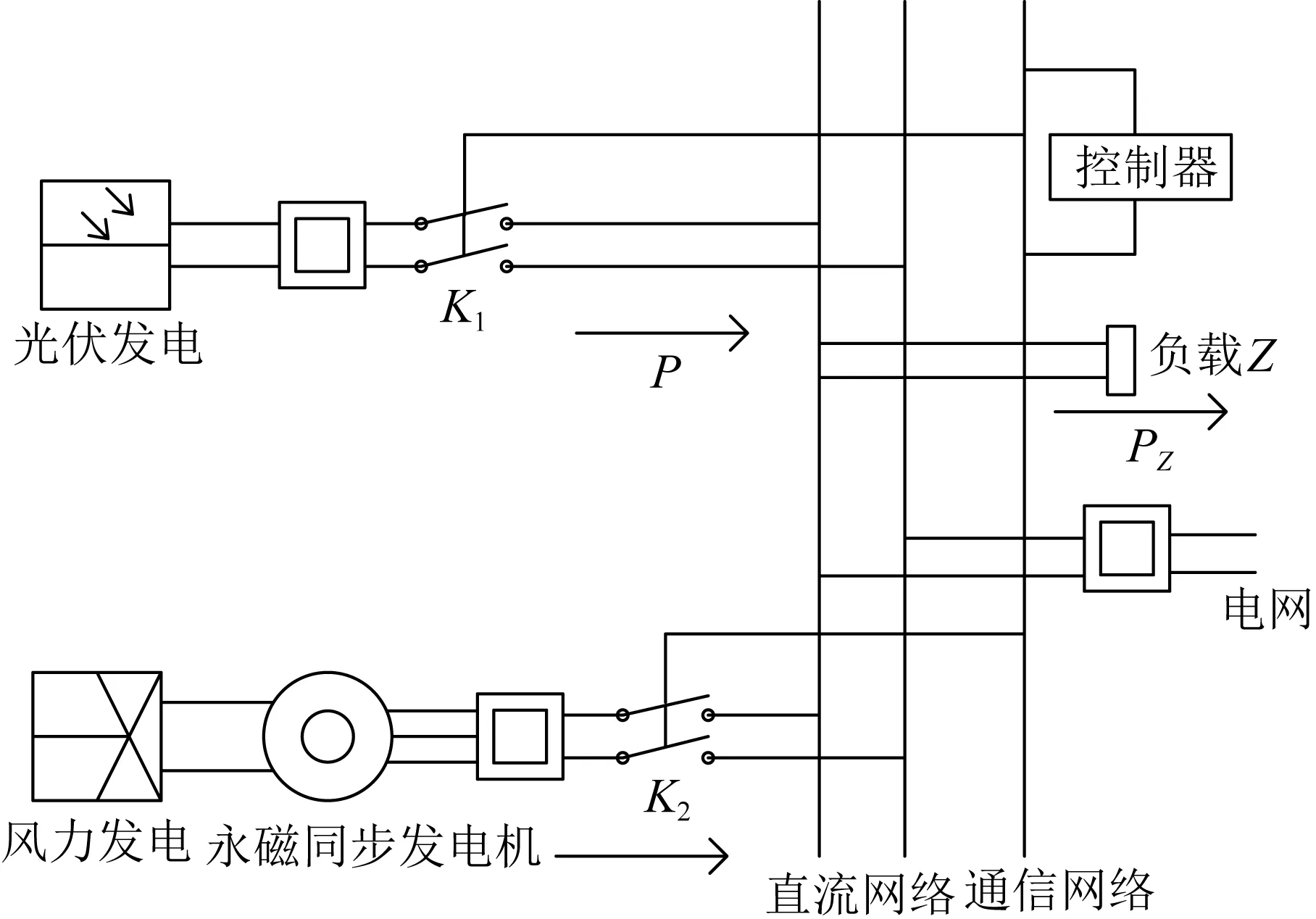
圖3 風光微電網直流發電系統結構示意圖

風能與太陽能作為清潔能源,其取之不盡可再生的特點使得應用風能與光能發電的理念越來越普及.由于風能與光能作為自然能源是不可控的,因此采用Markov跳變系統對光伏發電與風力發電系統進行建模,使2種發電模式在實際中可以互補,最大程度保障發電系統的穩定性.

根據該微電網系統結構圖,令rt=i={1,2}表示2種跳變模式,系統發電在光伏與風能之間進行切換.令x1(t)表示發電端輸出功率,x2(t)表示負載功率.相關控制系統的參數矩陣為:

Markov跳變系統的轉移概率和外部攻擊參數與例1相同.利用LMI工具箱,可以求得控制器的反饋增益為:

混雜驅動桿狀圖如圖4所示,狀態響應曲線如圖5所示.

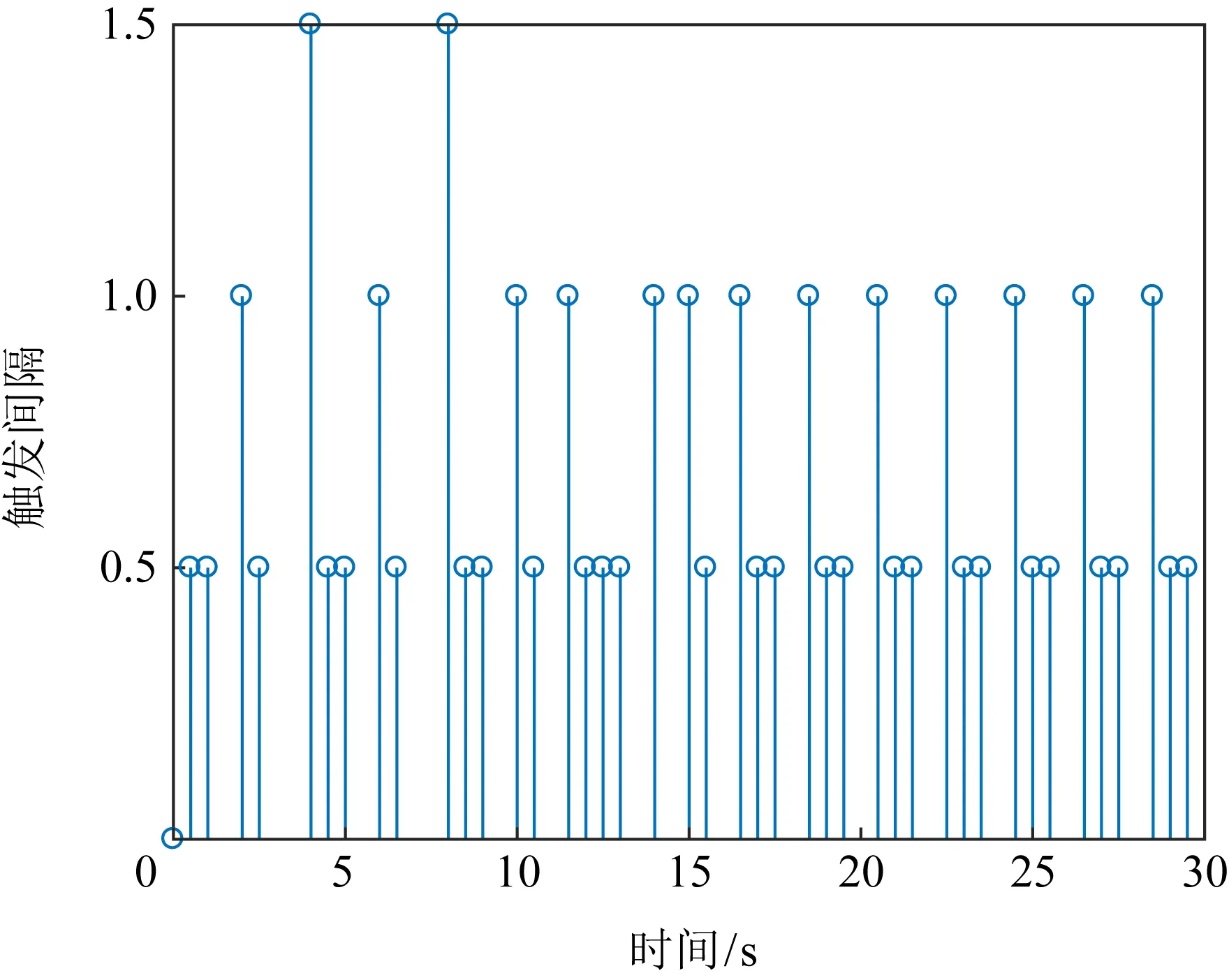
圖4 觸發桿狀圖(例2)

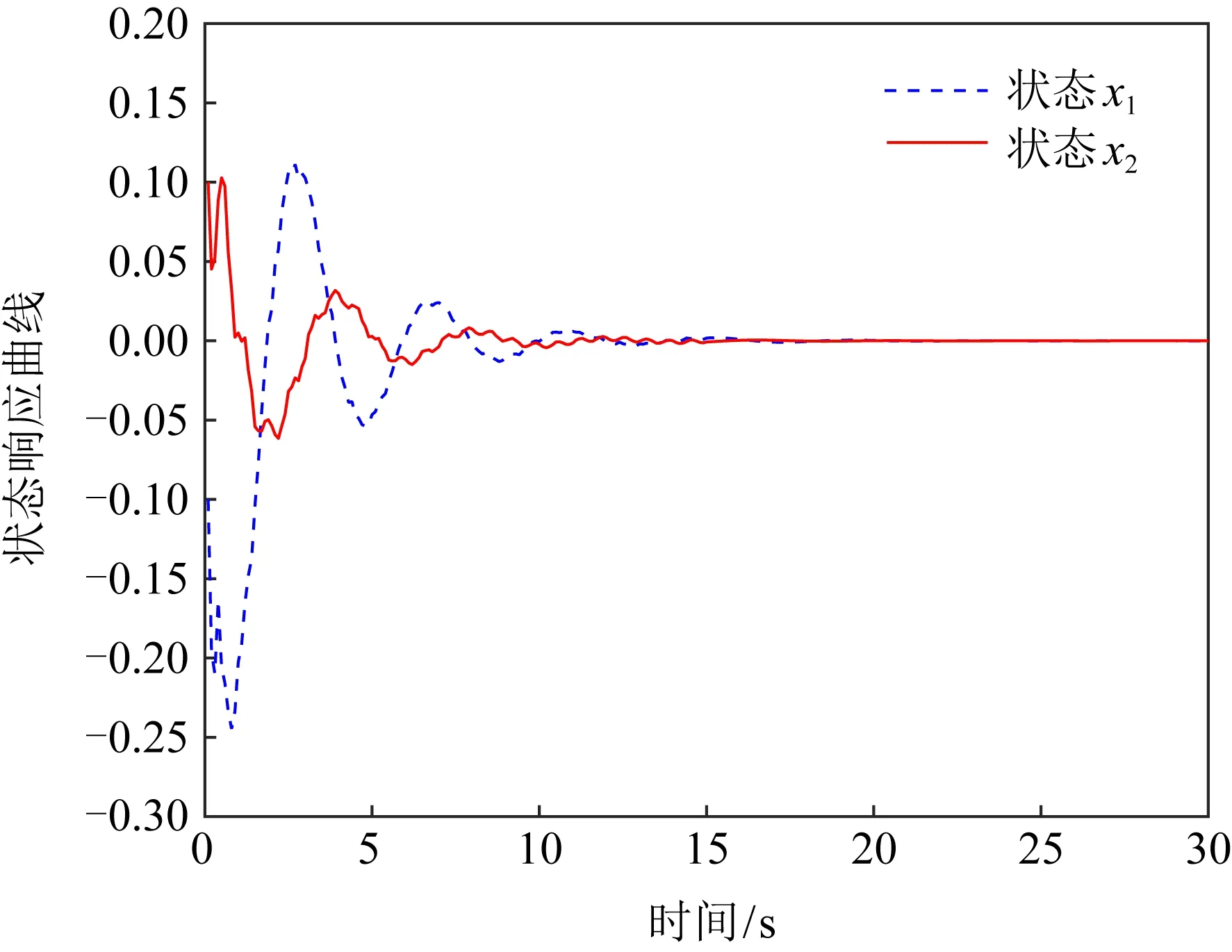
圖5 狀態響應曲線(例2)

從圖4與圖5可以看出,當微電網系統在遭遇外部攻擊時,系統依然可以在有限時間內保持穩定狀態,表明了本文推導的定理在實際應用中依然具備有效性.

4 結 論

本文針對基于混雜驅動機制和量化的Markov跳變系統有限時間輸出反饋控制進行了研究,利用伯努利分布統一了時間觸發機制和事件觸發機制,在數據傳輸與系統性能之間確定了新的平衡關系.在傳感器-控制器和控制器-執行器2個通道設置了對數量化器,降低通信網絡的帶寬占用率.此外,考慮當前工業網絡安全問題,將相關的網絡攻擊模型引入系統.利用線性矩陣不等式,給出了系統在有限時間穩定的充分條件,并利用仿真驗證了提出的定理的有效性,表明當系統遭受外部的網絡攻擊時依然能夠在有限時間內維持穩定.在未來的研究計劃中,我們將在現有的研究基礎上,在Markov跳變系統中引入模糊控制與神經網絡,以研究在不同的控制作用下系統的各項性能差異.