基于長電偶極子和大磁圓環的新型電磁矢量傳感器雙基地多輸入多輸出雷達角度和極化參數聯合估計*

謝前朋 潘小義 陳吉源 肖順平

(國防科技大學, 電子信息系統復雜電磁環境效應國家重點實驗室, 長沙 410073)

針對常規雙基地電磁矢量傳感器多輸入多輸出(multiple-input multiple-output, MIMO)雷達中短電偶極子 ( L/λ<0.1) 和小磁環 ( 2π(R/λ)<0.1) 輻射效率不足問題, 本文根據實際應用中電磁矢量傳感器的有效長度來設計新型的發射電磁矢量傳感器陣列和接收電磁矢量傳感器陣列.首先, 通過平行因子算法來實現對雙基地MIMO 雷達陣列接收數據空時特性的充分利用.這種處理過程能夠實現發射俯仰角和接收俯仰角的自動參數配對.然后, 針對歸一化坡印亭矢量估計器在長電偶極子和大磁圓環約束下無法實現角度和極化參數有效測量的問題, 對于利用平行因子算法得到的發射和接收加載矩陣采用新的盲估計算法來實現對角度參數和極化參數的高精度估計.所提出的盲估計算法在不需要電偶極子長度和磁環周長的先驗信息的情況下能夠有效地實現發射四維參數和接收四維參數的精確估計, 且該算法估計得到的八維參數滿足自動參數配對特性.最后, 詳細推導了長電偶極子和大磁圓環約束下雙基地MIMO 雷達中角度和極化參數估計性能的克拉美羅界.仿真實驗表明, 對于實際中長電偶極子和大磁圓環組成的新型電磁矢量傳感器, 本文所提算法具有良好的參數估計性能.通過理論分析和仿真實驗結果可以發現, 本文的研究工作能夠進一步促進電磁矢量傳感器在雙基地MIMO 雷達中的應用.

1 引 言

近年來, 電磁矢量傳感器陣列(electromagnetic vector sensors, EMVS)由于其優良的電磁測量能力得到了眾多學者的廣泛研究[1?5].相比于標量陣列, 電磁矢量傳感器通過利用其包含的三個相互正交的電偶極子和三個相互正交的磁偶極子分別實現對電場矢量和磁場矢量信息的獲取.隨著對電磁矢量傳感器研究的深入, 眾多學者把電磁矢量傳感器應用于集中式多輸入多輸出(multiple-input multiple-output, MIMO)雷達中, 以此來獲取MIMO 雷達中目標參數的極化信息[6?13].本文主要研究電磁矢量傳感器在雙基地MIMO 雷達中的應用.

由于每個電磁矢量傳感器包含6 個極子, 因此把電磁矢量傳感器應用于雙基地MIMO 雷達中面臨著復雜的角度參數和極化參數提取問題.為了實現對雙基地EMVS-MIMO 雷達中發射四維參數和接收四維參數的有效估計, 文獻[6]首次利用旋轉不變子空間算法(estimation of signal parameters via rotational invariance techniques, ESPRIT)來實現對二維發射角(two dimensional direction-ofdeparture, 2D-DOD)和二維接收角(two dimensional direction-of-arrival, 2D-DOA)的聯合參數估計.但是, 文獻[6]提出的ESPRIT 算法由于需要進行奇異值分解過程, 具有較大的計算復雜度.為了降低計算代價, 文獻[7]利用傳播算子方法(propagator method, PM)來實現對陣列接收數據信號子空間的近似.文獻[8]進一步考慮利用EMVSMIMO 雷達陣列接收數據的多維特性, 提出高階奇異值分解算法(high order singular value decomposition, HOSVD)來實現對角度參數和極化參數的聯合估計.以上三種算法面臨的主要問題在于都需要進行構建額外的譜峰搜索類配對優化函數來實現2D-DOD 和2D-DOA 的參數配對.譜峰搜索類配對函數的構建, 進一步增加了額外的計算復雜度.為了實現2D-DOD 和2D-DOA 的自動參數配對, 文獻[9]提出平行因子算法.該算法利用平行因子多次迭代得到的加載矩陣包含的內部固有特性來實現對發射俯仰角和接收俯仰角的角度參數配對.文獻[10]在文獻[7]的基礎之上提出修正的傳播算子算法, 該算法通過對發射角和接收角利用相同的特征矢量矩陣求解來實現參數配對過程.文獻[11]通過設計稀疏的發射陣列和接收陣列來實現對雙基地EMVS-MIMO 雷達中角度參數和極化參數估計性能的提升.文獻[12,13]針對雙基地EMVSMIMO 雷達中的相關信源展開研究.

以上提出的針對雙基地EMVS-MIMO 雷達中的角度參數和極化參數估計算法主要還是在短電偶極子 ( L/λ<0.1) 和小磁環 ( 2π(R/λ)<0.1) 組成的理想電磁矢量傳感器約束下進行研究.但是, 實際中常用的電偶極子的長度和磁偶極子的周長一般情況下不滿足上述約束[14?19], 即 L /λ>0.1 和2π(R/λ)>0.1.究其原因在于, 短電偶極子((L/λ)<0.1) 和小磁環 ( 2π(R/λ)<0.1) 組成的電磁矢量傳感器不能有效地實現電磁輻射, 影響接收端的參數估計精度.因此, 為了適應實際目標探測的需要, 本文考慮長電偶極子和大圓環組成的電磁矢量傳感器發射陣列和接收陣列背景下的雙基地MIMO 雷達的角度參數和極化參數估計問題.相比于文獻[6?13]中的短電偶極子和小磁環, 為了提取長電偶極子和大圓環組成的新型電磁矢量傳感器中的角度信息和極化信息, 本文利用新的估計方法來避免歸一化坡印亭矢量估計器的失效問題.本文提出的盲估計方法能夠實現角度參數和極化參數高精度的求解.通過對新型電磁矢量傳感器約束下的雙基地MIMO 雷達進行詳細的理論推導,能夠進一步解決實際面臨的角度和極化參數估計問題, 且通過設計不同的仿真實驗進一步對電偶極子長度和磁環周長的選擇提供了相應的技術支撐.

2 信號模型

2.1 長電偶極子和大磁圓環組成的新型電磁矢量傳感器陣列信號模型

如圖1 所示, 電磁矢量傳感器包含三個相互正交的電偶極子和三個相互正交的磁環, 其中三個正交的電偶極子和磁環分別被用來實現對電場矢量和磁場矢量的測量.

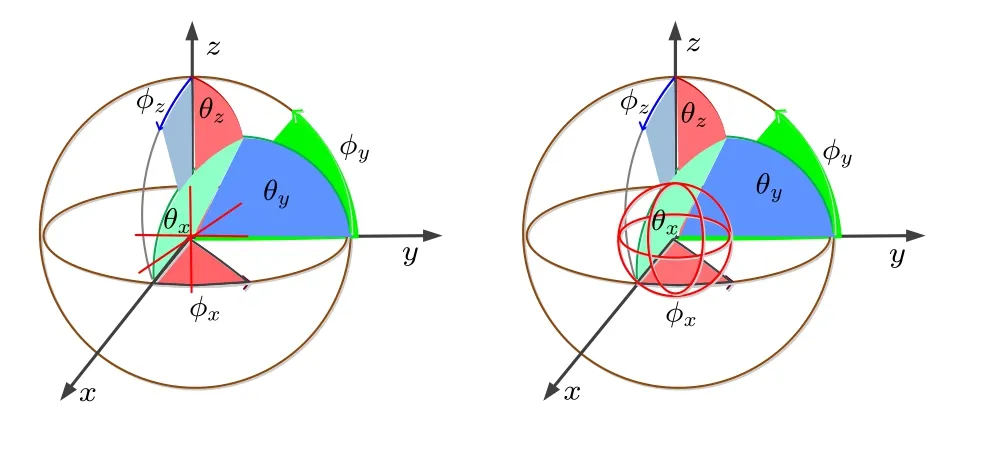
圖1 三正交電偶極子和三正交磁環示意圖Fig.1.Three orthogonal dipoles and three orthogonal loops.

考慮一個電磁波信號以角度 ( θz,?x,γ,η) 入射到直角坐標系中, ( θz,?x) 分別表示入射信號的俯仰角和方位角, 角度范圍分別為 θz∈[0,π) , ?x∈[0,2π).γ 和 η 分別表示極化角和極化相位差, 相應的角度范圍分別為 γ ∈[0,π/2] , η ∈[?π,π).同時根據圖1中的空間坐標, θx∈[0,π] 表示入射信號的傳播方向和正x 軸的夾角; θy∈[0,π] 表示入射信號的傳播方向和正y 軸的夾角; ?y∈[?π,π] 表示信源傳播方向在 y -o-z 平面的投影和正y 軸的夾角;?z∈[?π,π] 表 示信源傳播方向在 x -o-z 平面的投影和正z軸的夾角.以上各個角度與入射信號的方位角和俯仰角的關系如下:

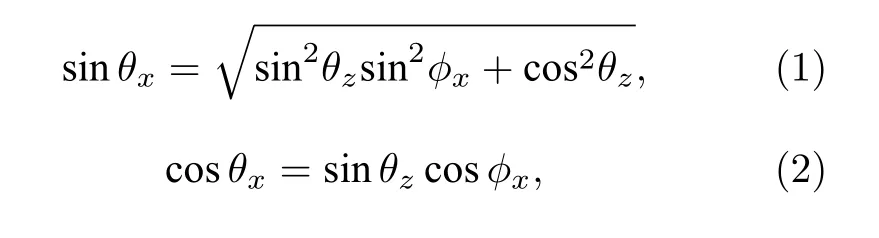
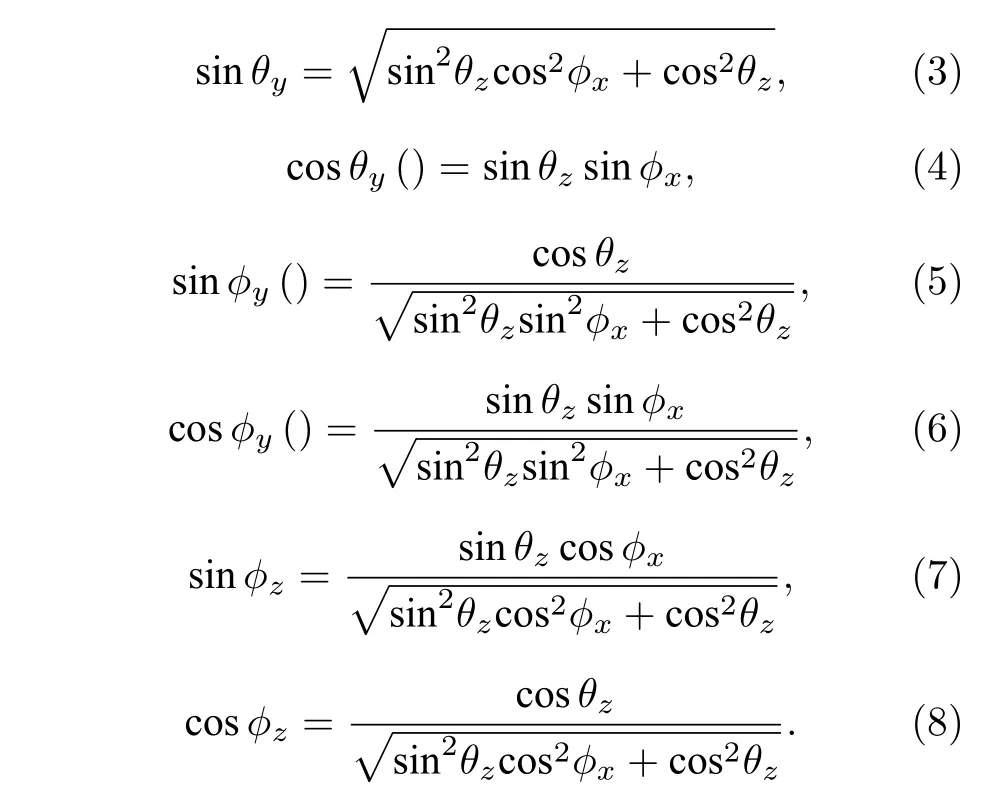
定義如下的單位矢量 uθx, uθy, uθz和u?x

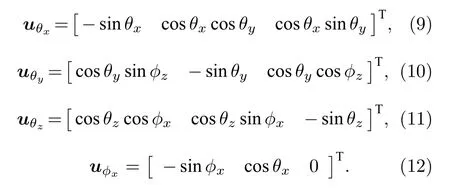
根據圖1 可以看出, 在直角坐標系下入射目標的電磁場域矢量可以分別表示為

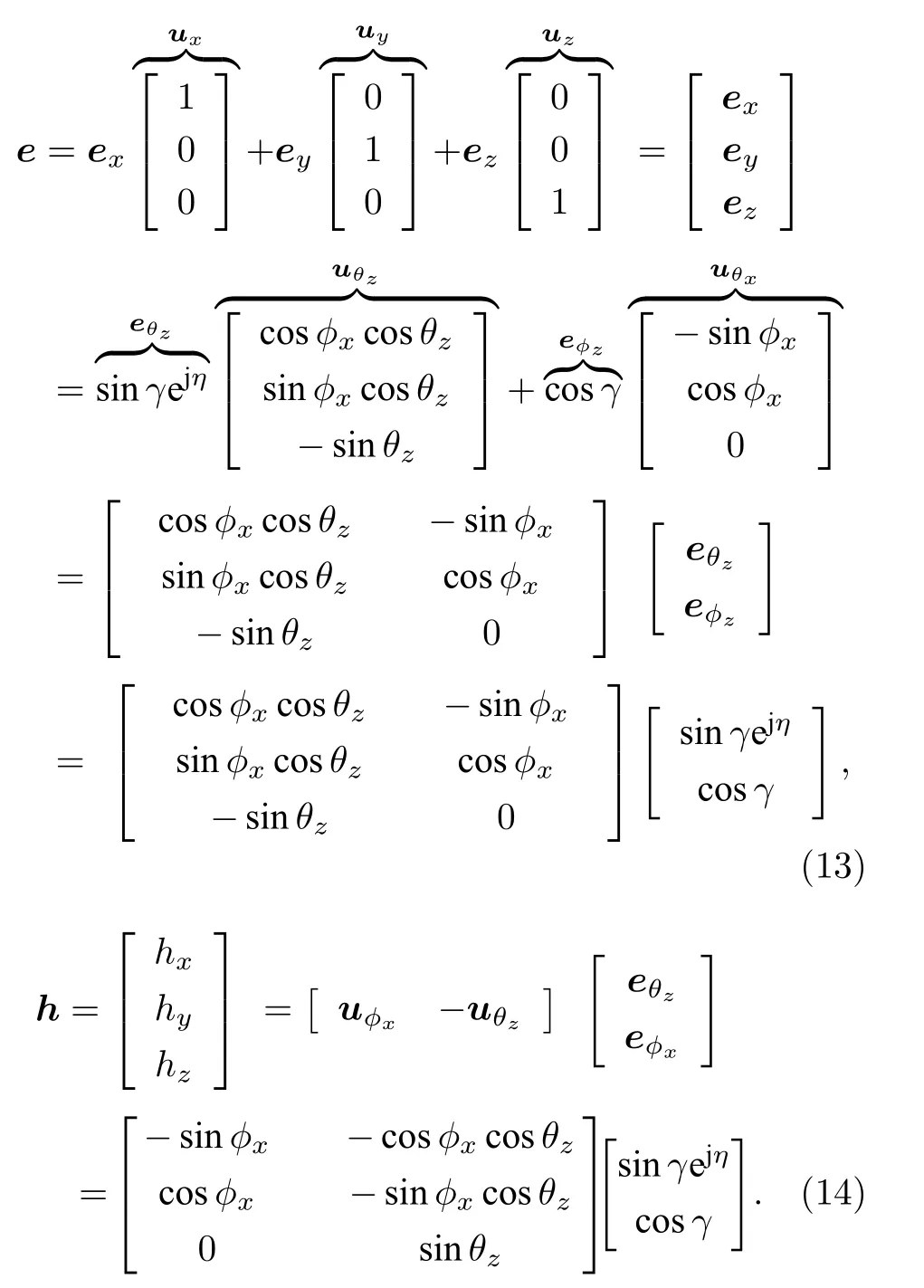
因此, 理想電磁矢量傳感器的空間響應可以表示為

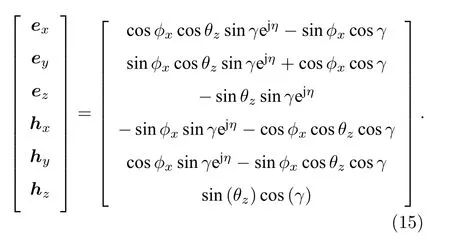
在文獻[17?19]中, 針對長電偶極子和大圓環背景下的三正交電偶極子和三正交磁偶極子進行了詳細的分析.根據文獻[17?19]中的推導, 下面給出長電偶極子和大圓環背景下新的電場矢量和磁場矢量.實際中常用的電偶極子的長度一般滿足 L /λ>0.1 , 例如半波長偶極子.同樣地, 常用的磁偶極子的長度也要求滿足 2 π(R/λ)>0.1 ,如單位波長磁環.對于長電偶極子組成的三正交陣列, 其電場矢量并不是僅僅等于理想的電場矢量 e 和標量數據的乘積, 相反其是一個電場矢量e和三元組有效長度 le的點乘.其中,le的詳細形式為

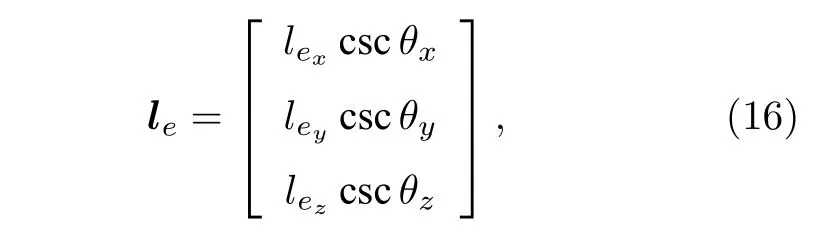
其中, θx∈[0,π) 表示入射信源的傳播角和x 軸的夾角, θy∈[0,π) 表示入射信源的傳播角和y 軸的夾角, 且

電偶極子的有效長度不僅僅取決于偶極子自身的物理長度, 還與入射信號的自身波長有關.同樣地, 實際中三正交磁環的磁場矢量也是 h 和三元組有效長度 lh的點乘=h·lh.lh的詳細形

式為

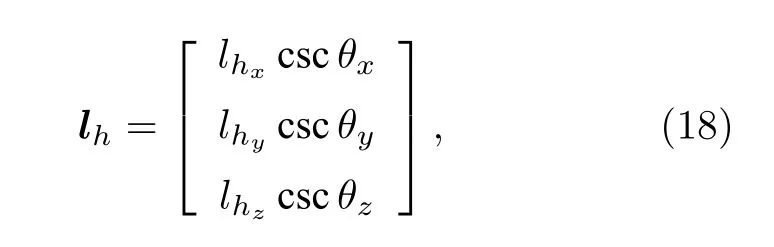
其中

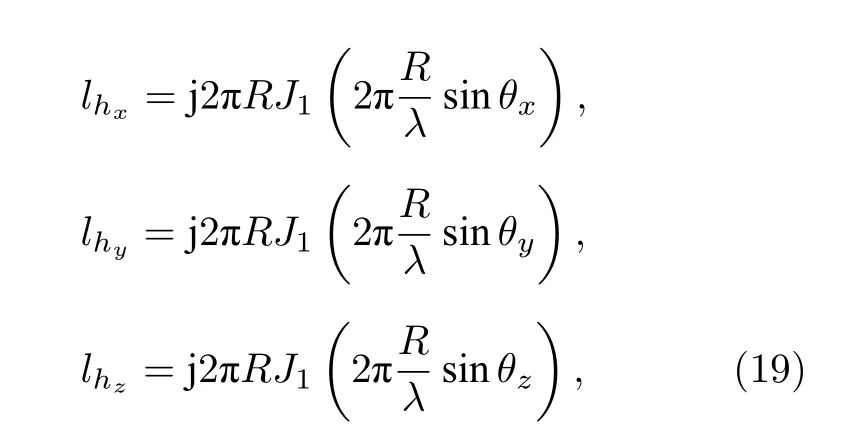
其中, J1(·) 表示一階第一類貝塞爾函數.因此, 一個包含三正交的長電偶極子和三個相互正交的大磁環構成的六元電磁矢量傳感器, 其詳細的電場形式和磁場形式可以表示為

通過對(15)式和(20)式的對比可以發現, 為了實現角度參數和極化參數的求解, 常用的歸一化坡印亭矢量處理方法在長電偶極子和大磁圓環的約束下失效.因此, 為了解決實際雙基地EMVSMIMO 雷達中的角度參數和極化參數估計問題,在接下來的分析中, 通過尋找新的處理手段來實現長電偶極子和大磁圓環組成的新型EMVS 背景下的目標參數估計.

2.2 長電偶極子和大磁圓環約束下雙基地EMVS-MIMO 雷達信號模型

如圖2 所示, 考慮一個包含M 個長電偶極子和大磁圓環組成的新型EMVS 發射陣列和N 個長電偶極子和大磁圓環組成的新型EMVS 接收陣列的雙基地 EMVS-MIMO 雷達系統, 其中發射陣列和接收陣列的陣元間距均是半波長.且發射EMVS 陣列和接收EMVS 陣列中長電偶極子的長度和大磁環的周長分別設置為 L ((L/λ)>0.1) 和R (2π(R/λ)>0.1).因此, 新型發射EMVS 陣列和新型接收EMVS 陣列的陣元位置為

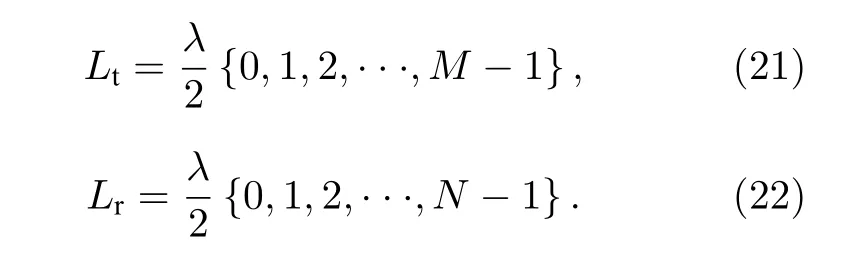
假設目標的個數為K, 則長電偶極子和大圓環磁偶極子組成的發射 EMVS 導向矢量和接收EMVS 導向矢量分別為

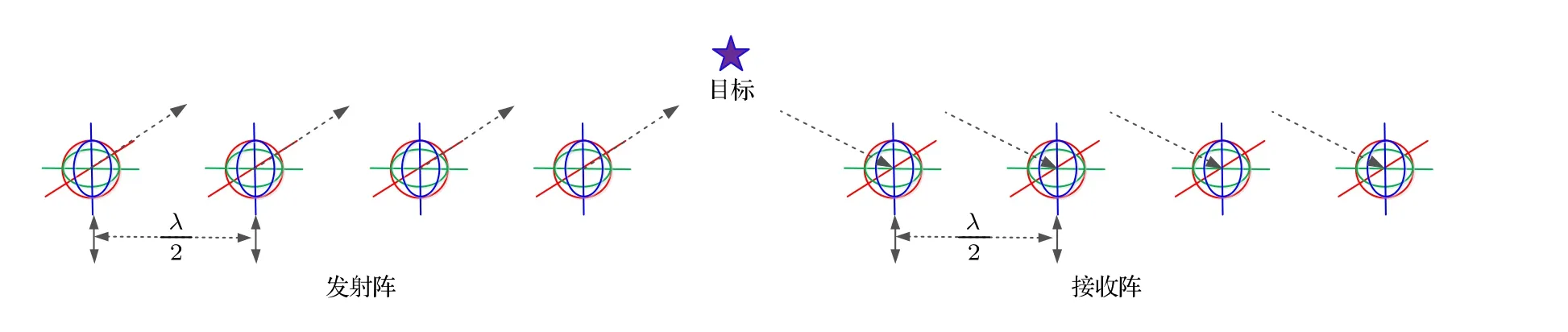
圖2 長電偶極子和大磁圓環組成的新型雙基地EMVS-MIMO 雷達系統示意圖Fig.2.New designed bistatic EMVS-MIMO radar system with long dipoles and large loops.

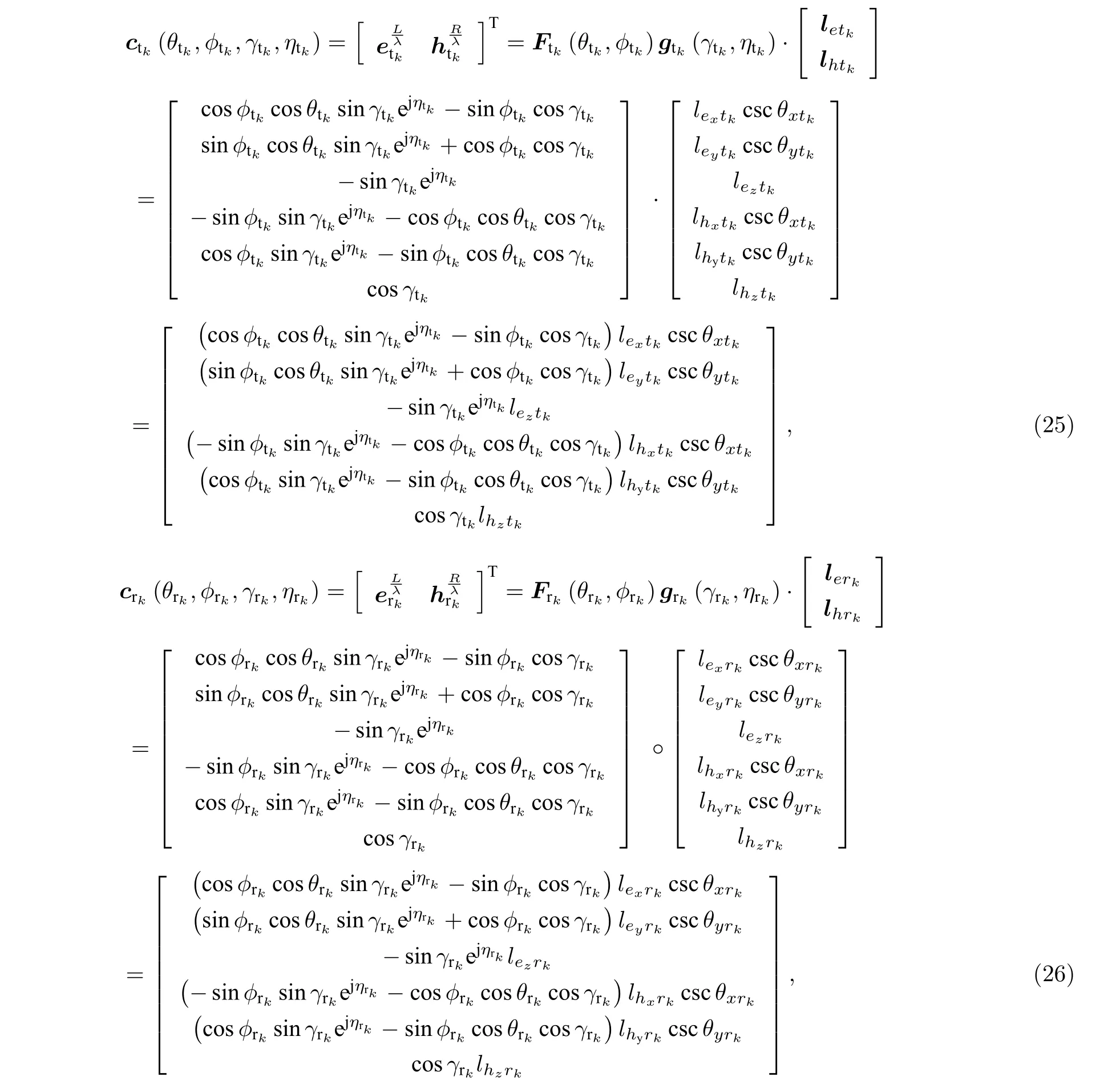
其中, Ftk(θtk,?tk) 和 Frk(θrk,?rk) 表示維度為6×2的空間角度位置矩陣, 且 θtk,θrk∈[0,π) 表示俯仰角, ?tk,?rk∈[0,2π) 表示方位角.gtk(γtk,ηtk) 和grk(γrk,ηrk) 表示維度為 2 ×1 的極化狀態矢量, 且γtk,γrk∈[0,π/2] 表 示極化角, ηtk,ηrk∈[?π,π] 表示極化相位差.其 中, θxtk, θytk, θxrk, θyrk, lextk,leytk, leztk, lhxtk, lhytk, lhztk, lexrk, leyrk, lezrk,lhxrk, lhyrk, lhzrk的詳細形式可以根據(1)式—(8)式, (17)式和(19)式來獲得.

據(15)式和(20)式可見, 由于長電偶極子和大圓環磁偶極子的空間電磁響應和理想的短電偶極子和小磁環對應的空間電磁響應不同, 因此, 常用的矢量叉積算法并不能有效地實現發射四維參數和接收四維參數的求解.為了實現長電偶極子和大磁圓環背景下的發射四維參數和接收四維參數求解, 在下一章節將采用有效的盲校正方法.

進一步地, 利用雙基地 EMVS-MIMO 雷達發射信號波形和接收信號波形的正交性, 匹配濾波之后的陣列接收數據可以表示為[6]

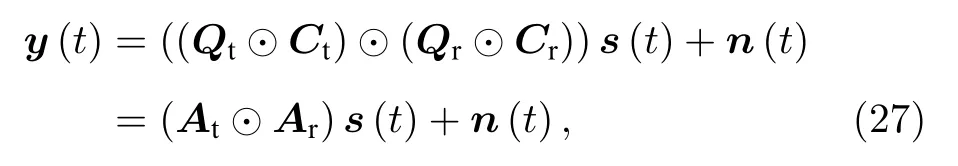
其中 At=[at1,at2,···,atK] 和Ar=[ar1,ar2,···,arK]分別表示發射導向矢量矩陣和接收導向矢量矩陣,n(t)表示加性高斯白噪聲矢量.對于T 個采樣快拍, 總的陣列接收數據可以表示為

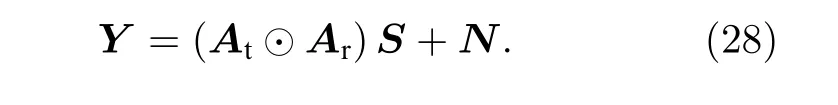
對于長電偶極子和大圓環磁偶極子組成的雙基地EMVS-MIMO 雷達, 其陣列接收數據的結構仍然具有空時特性.因此, 為了充分考慮發射陣列、接收陣列和采樣快拍之間的內在聯系, 這里采用張量結構來對陣列接收數據進行處理.

3 基于新型盲估計算法的聯合角度和極化參數估計

3.1 高分辨聯合角度和極化參數估計

根據文獻[20]中平行因子分解的定義, (28)式中的陣列接收數據可以進一步的被重新表示為

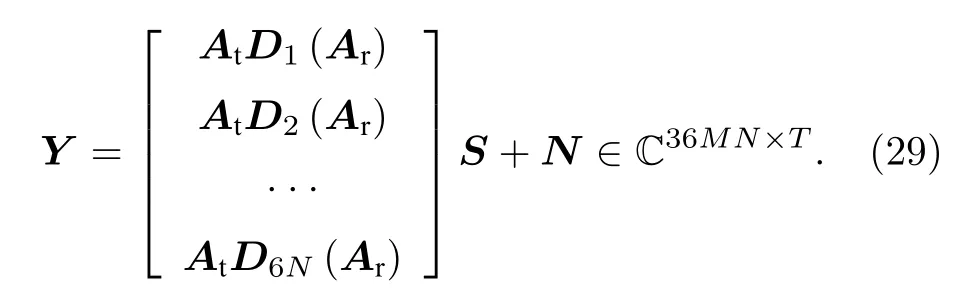
相應地, 關于發射導向矢量矩陣 At和接收導向矢量矩陣 Ar的聯立方程可以分別被表示為

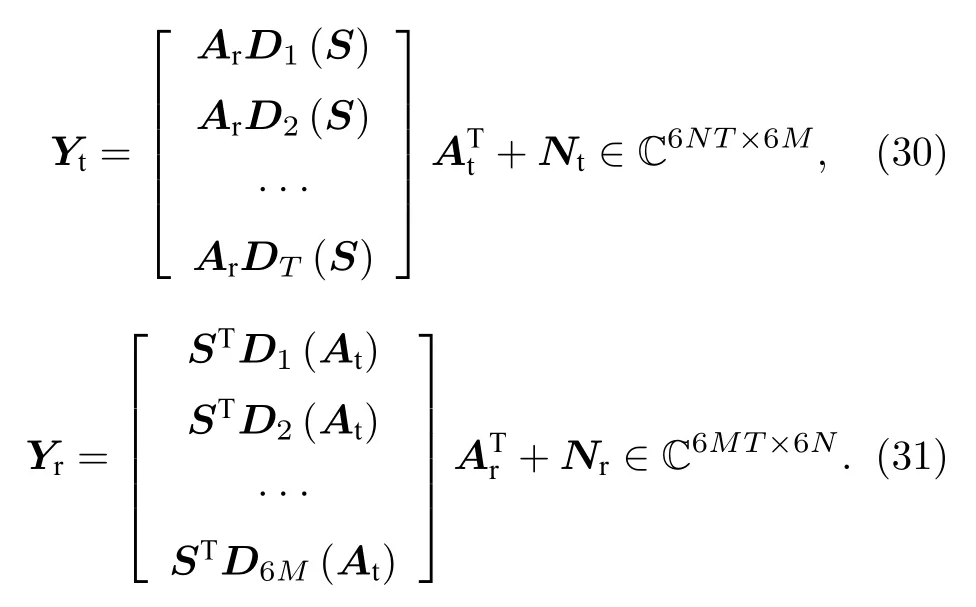
通過文獻[9,11]中相同的處理方式, 利用平行因子分解算法的多次迭代過程, 最終能夠實現對加載矩陣和的有效求解.并且, 包含在和中的2 D-DOD 和2 D-DOA 是自動配對的.下面分別針對估計得到的發射導向矢量矩陣和接收導向矢量矩陣進行發射俯仰角、發射方位角、發射極化角、發射極化相位差和接收俯仰角、接收方位角、接收極化角、接收極化相位差的估計.

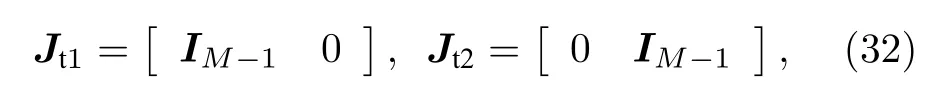
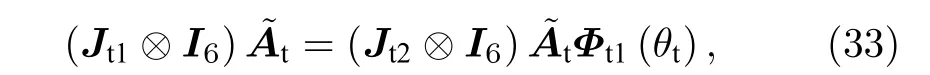
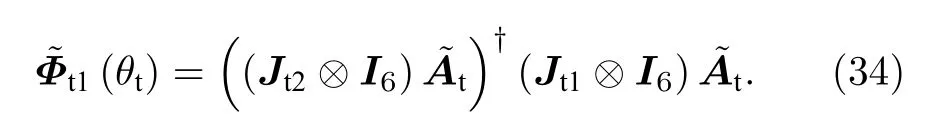
進一步地, 估計得到的發射俯仰角的正弦值可以表示為

因此, 相應的發射俯仰角可以被表示為

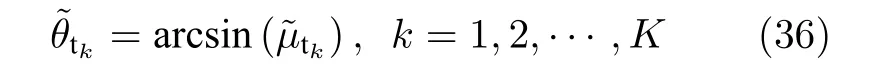
當獲得發射陣列的俯仰角之后, 為了實現發射方位角、發射極化角和極化相位差的求解, 首先,通過如下的方式獲得長電偶極子和大圓環磁偶極子組成的新型EMVS 陣列的空間響應函數

圖3 新型陣列 EMVS-MIMO 雷達系統旋轉不變關系構建Fig.3.The rotational invariance relationship for new designed bistatic EMVS-MIMO radar system.

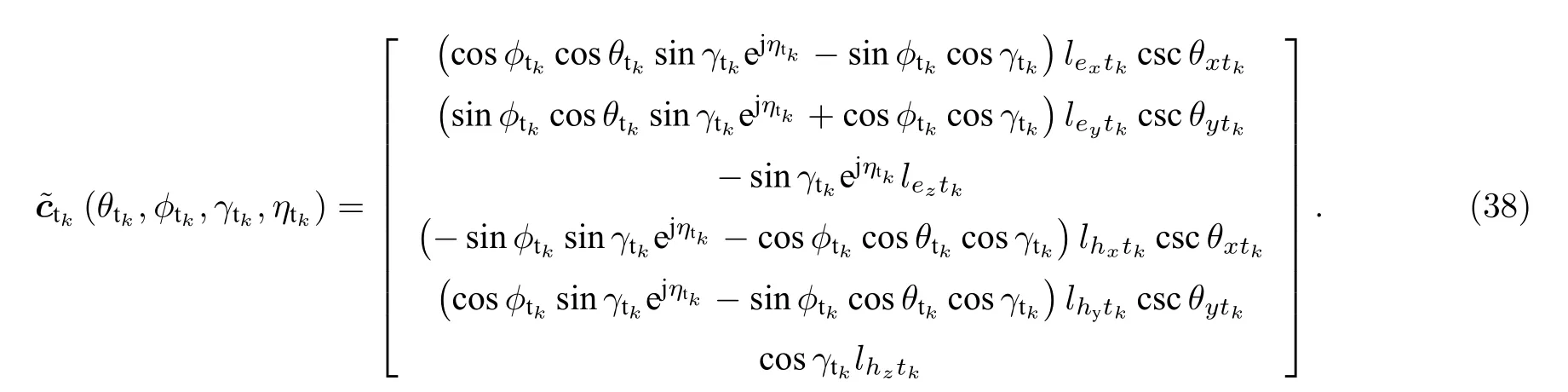
下面利用盲估計算法實現對 ( ?tk,γtk,ηtk) 進行角度參數估計.

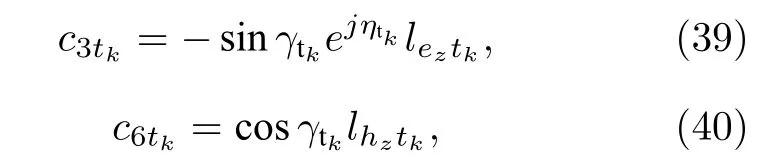
則估計得到的極化相位差可以被表示為

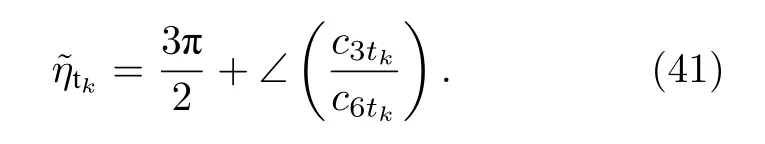
如果 L /λ>0.1 和 2 π(R/λ)>3.8317 , 根據(17)式和(19)式中的 lez和 lhz的定義, 此時二者的取值為負, 因此以上對 ηtk的求解需要進行加 π 來實現相應的相位補償.下面對 ?tk進行求解, 首先, 通過下面的操作去除 c1tk中的相位信息

進一步地, 通過如下的求解方式從(42)式中的復值中移除實數因子lextkcsc θxtk

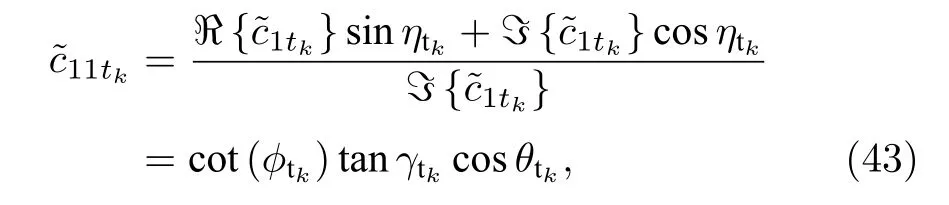
其中, ? 表示實部, ? 表示虛部.類似地, 為了去除c2tk中的相位信息, 構建如下的求解過程

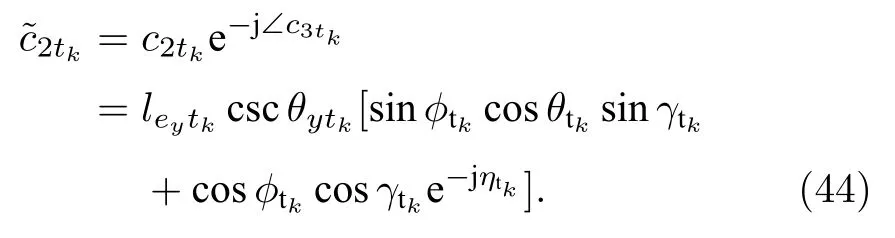
通過如下的求解方式從(44)式中的復值中移除實數因子leytkcsc θytk

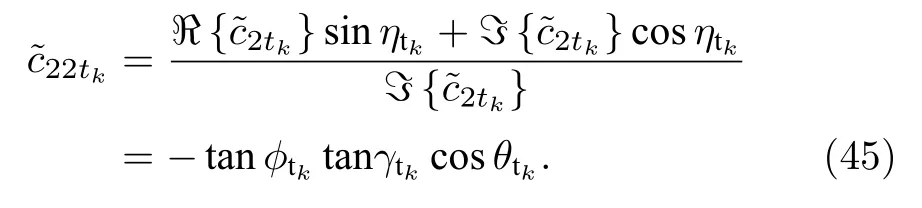
對等式(43)式和(45)式進行分析可以發現,在已經估計得到極化相位差 η ?tk之后, 通過的相除可以去除兩者中的公共因子 t an γtkcos θtk.除過之后的變量僅僅是關于 ?tk的, 因此, 入射信源的方位角估計可以表示為

在求得極化相位 差 ηtk和 方位角 ?tk之后, 下面進行對極化角 γtk的求解.

通過如下的方式去除 c4tk中的相位信息

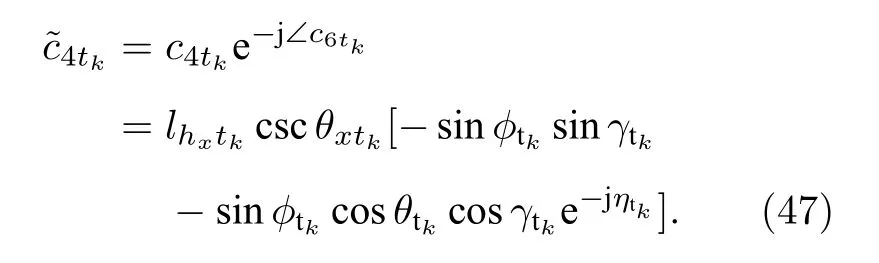
類似地, 去除 c5tk中的相位信息, 可以進一步被表示為

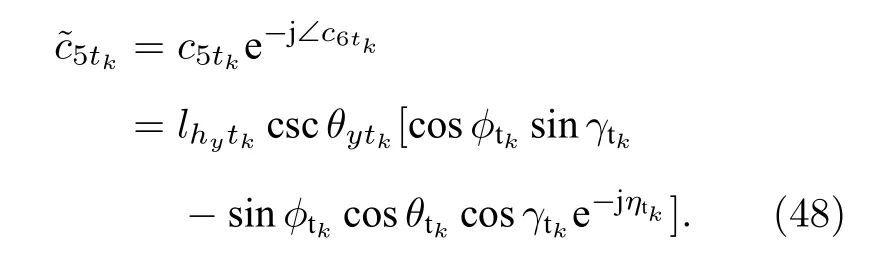
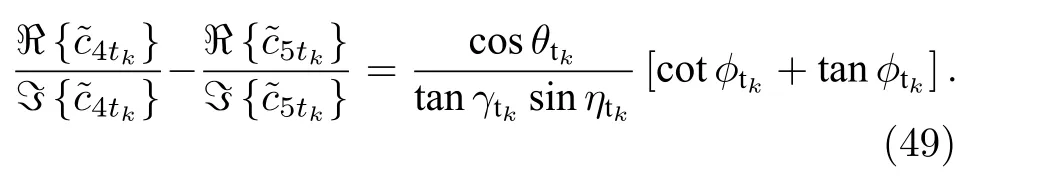
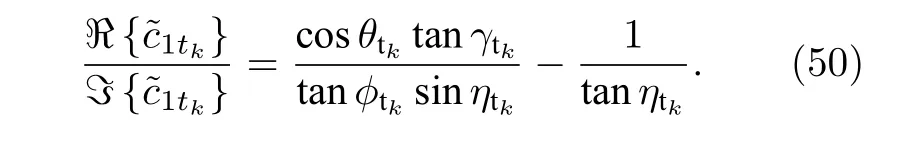
進一步地把(49)式和(50)式進行相除, 可以得到

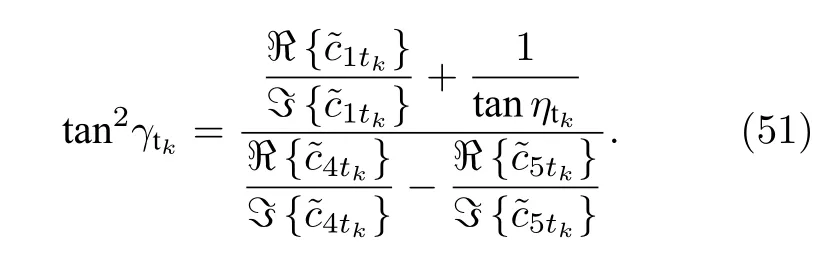
從(51)式可以看出, 在已經獲得極化相位差ηtk和方位角 ?tk之后, (51)式僅僅與極化角 γtk有關.最終, 估計得到的極化角可以被表示為

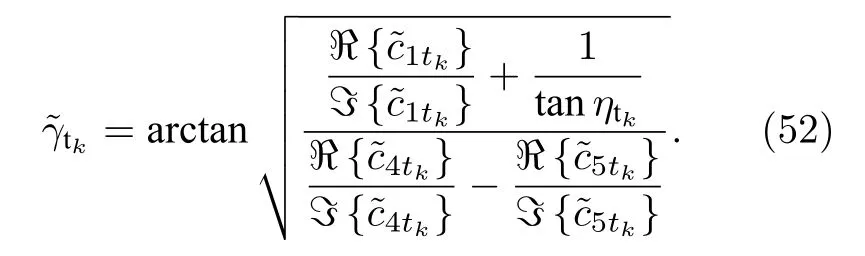
因此, 經過上面的求解之后, 最后可以得到長電偶極子和大磁圓環組成的新型電磁矢量傳感器針對入射信源的發射四維參數.并且, 通過上面的分析可以發現, 以上的求解過程并不需要額外的以及極化角作為先驗信息, 完全實現了角度參數和極化參數求解的盲估計, 通過以上處理過程得到的滿足自動參數配對特性.

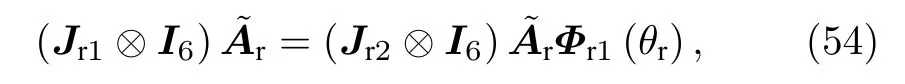
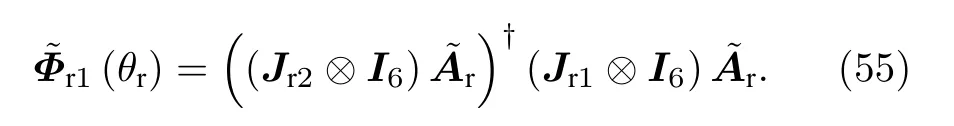
進一步地, 估計得到的接收俯仰角的正弦值可以表示為

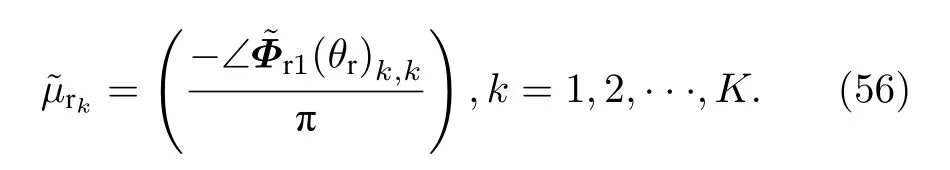
因此, 相應的接收俯仰角可以被表示為

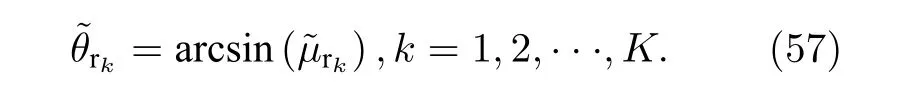
當獲得接收陣列的俯仰角之后, 為了實現接收方位角、接收極化角和極化相位差的求解, 通過如下方式首先獲得長電偶極子和大磁圓環組成的EMVS 陣列的空間響應函數

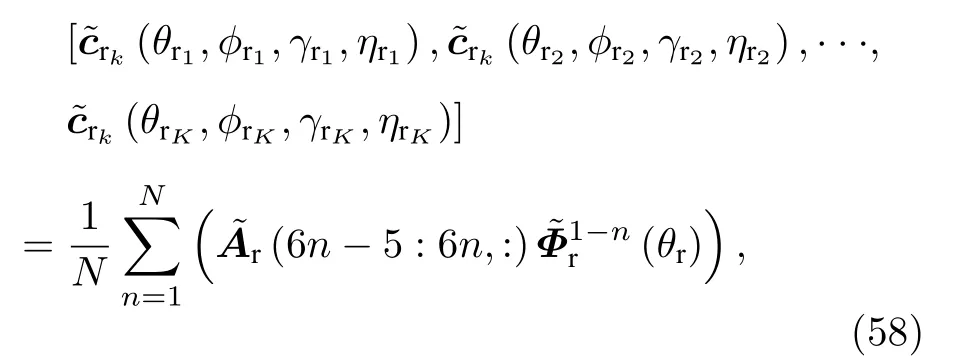
下面利用盲估計算法實現對 ( ?rk,γrk,ηrk) 進行角度參數估計.

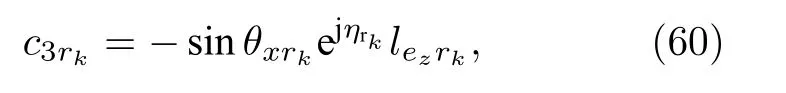
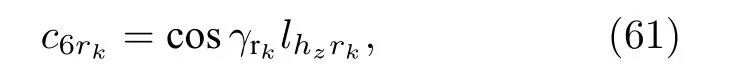
則估計得到的極化相位差可以被表示為

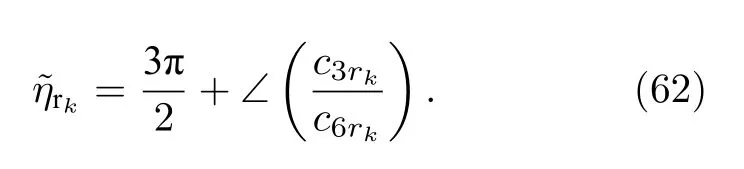
如果 L /λ>0.1 和 2 π(R/λ)>3.8317 , 根據(17)

式和(19)式中的 lez和 lhz的定義, 此時二者的取值為負, 因此以上對 ηrk的求解需要進行加 π 來實現相應的相位補償.下面對 ?rk進行求解, 首先, 通過下面的操作去除 c1rk中的相位信息

進一步地, 通過如下的求解方式從(63)式中的復值中移除實數因子lexrkcsc θxrk

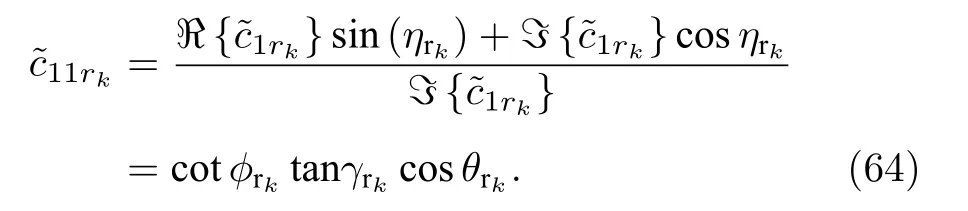
類似地, 為了去除 c2rk中的相位信息, 構建如下的求解過程

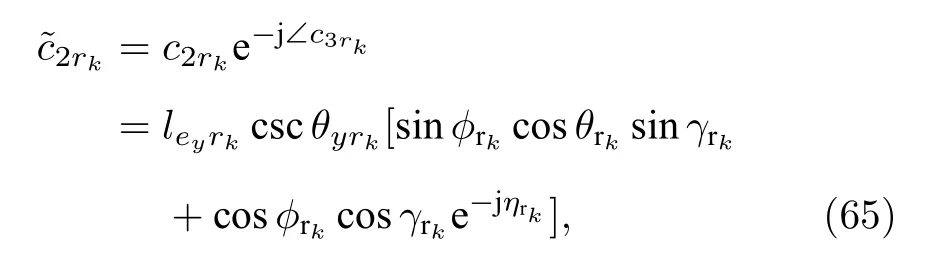
通過如下的求解方式從(65)式中的復值中移除實數因子leyrkcsc θyrk

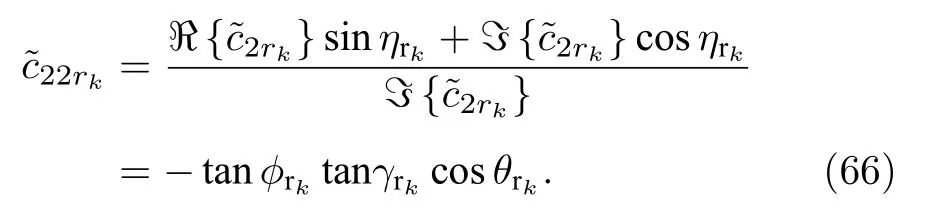
對等式(64)式和(66)式進行分析可以發現,在已經估計得到極化相位差之后, 通過的相除可以去除兩者中的公共因子 t an γrkcos θrk.除過之后的變量僅僅是關于 ?rk的, 因此, 入射信源的方位角估計可以表示為

在求得 極化相位差 ηrk和方位角 ?rk之后, 下 面對極化角 γrk進行求解.

通過如下的方式去除 c4rk中的相位信息

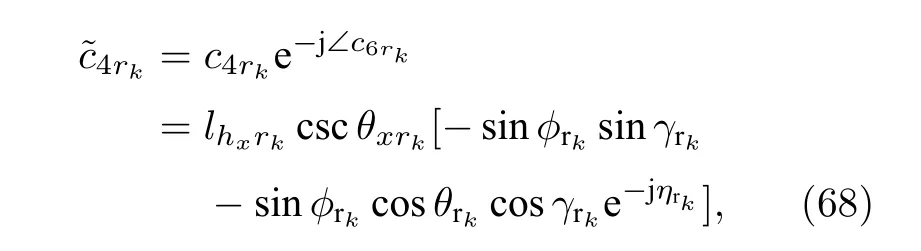
類似地, 去除 c5rk中的相位信息, 可以進一步被表示為

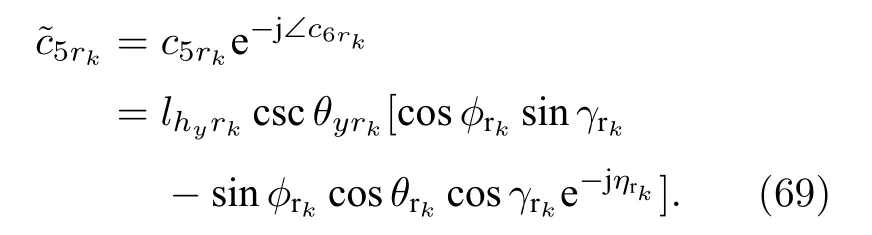
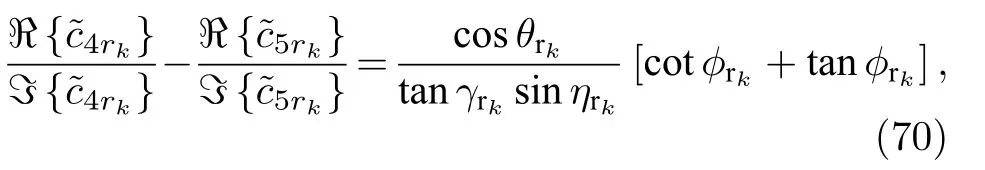
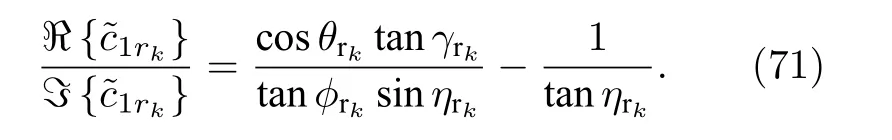
進一步把(70)式和(71)式進行相除, 可以得到

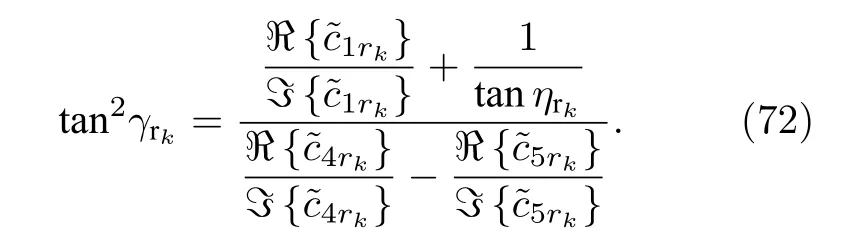
從(72)式中可以看出, 在已經獲得極化相位差 ηrk和方位角 ?rk之后, (72)式僅僅與極化角 γrk有關.最終, 估計得到的極化角可以被表示為

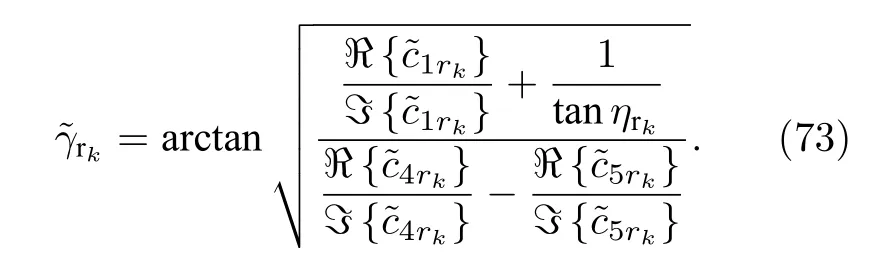
因此, 經過上面的求解之后, 最后可以得到長電偶極子和大磁圓環組成的新型電磁矢量傳感器針對于信源的接收四維參數.并且, 通過上面的分析可以發現, 以上的求解過程并不需要額外的以及極化角作為先驗信息, 完全實現了角度參數和極化參數求解的盲估計, 通過以上處理過程得到的滿足自動參數配對特性.

最終, 經過以上的算法處理, 得到的對應于發射 EMVS 陣列和接收 EMVS 陣列的發射俯仰角、發射方位角、發射極化角、發射極化相位差和接收俯仰角、接收方位角、接收極化角、接收極化相位差能夠保證良好的估計精度.

3.2 克拉美羅界(Cramer-Rao Bound)

由于長電偶極子的長度和大磁圓環的周長作為變量也影響著角度估計的精度, 對于所設計的新型長電偶極子和大磁圓環組成的EMVS 陣列, 雙基地EMVS-MIMO 雷達需要估計的參數分別為(θt,?t,γt,ηt,L,R) 和 ( θr,?r,γr,ηr,L,R) , 其中

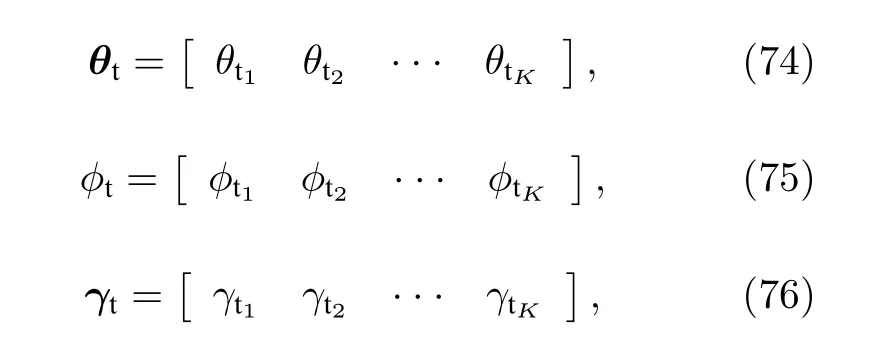
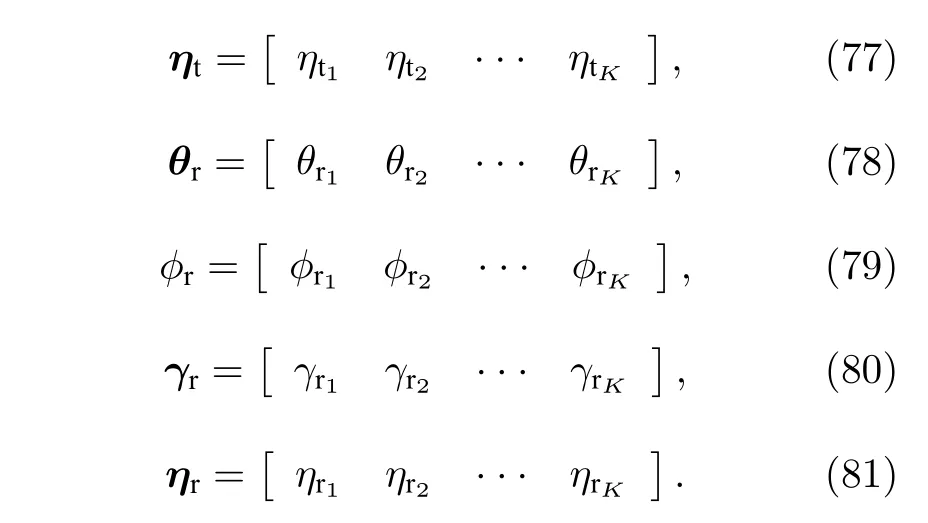
因此, 關于以上未知變量的Fisher 信息矩陣可以被表示為

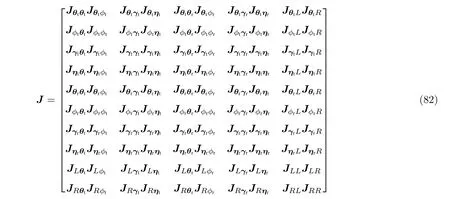
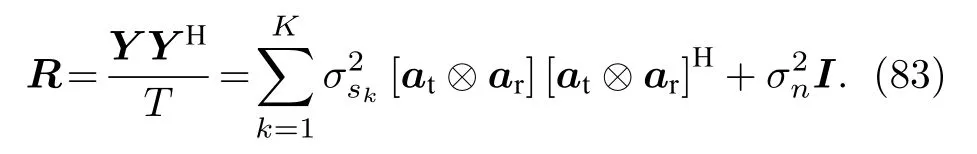
因 此, Fisher 信 息 矩 陣 J 關 于(θt,?t,γt,ηt,L,R)和 ( θr,?r,γr,ηr,L,R) 的詳細形式可以進一步被表示為[21]

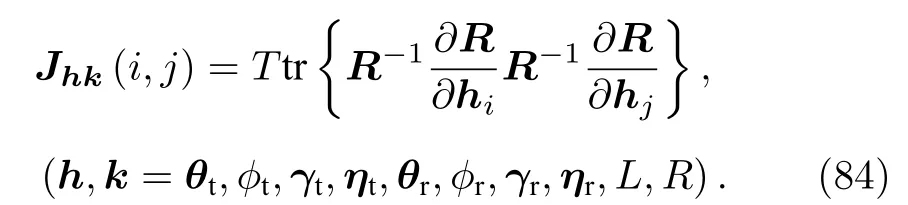
在附錄A 中, 詳細給出了Fisher 信息矩陣J中各個元素的推導過程.由于得到的Fisher 矩陣J滿足Hermitian 特性, 因此, 只需要知道上對角線的元素值即可獲得整個矩陣的值.最終, 對于獲得的 J , 對應于發射參數 ( θt,?t,γt,ηt,L,R) 和接收參數 ( θr,?r,γr,ηr,L,R) 的CRB 可以被表示

故, 經過以上的推導過程可以獲得CRB 的閉式解.

4 仿真實驗

下面通過一系列的仿真實驗來驗證所提算法對于發射四維參數和接收四維參數的參數估計性能.如圖2 所示, 發射EMVS 陣列和接收EMVS陣列均是由長電偶極子和大磁圓環組成, 其中發射陣列個數和接收陣列個數分別被設置為 M =6 和N =8.并且, 發射EMVS 陣列和接收EMVS 陣列的陣元間距均為半波長.

4.1 算法的角度參數自動配對特性

首先, 通過星座圖來驗證所提盲估計算法的角度參數自動配對的有效性.在仿真中, 長電偶極子的長度設置為 L /λ=0.5 , 大磁圓環的周長設置為2π(R/λ)=1.假設入射目標的個數 K =4 , 并且各個信號之間相互獨立, 相應的發射俯仰角、發射方位角、發射極化角、發射極化相位差和接收俯仰角、接收方位角、接收極化角、接收極化相位差如表1所列.仿真中噪聲設置為相互獨立的零均值加性高斯白噪聲, 并且信號和噪聲之間相互獨立.快拍數T 設置為200, 信噪比設置為 2 0 dB.利用100次蒙特卡羅仿真實驗結果來繪制如圖4 所示的星座圖.

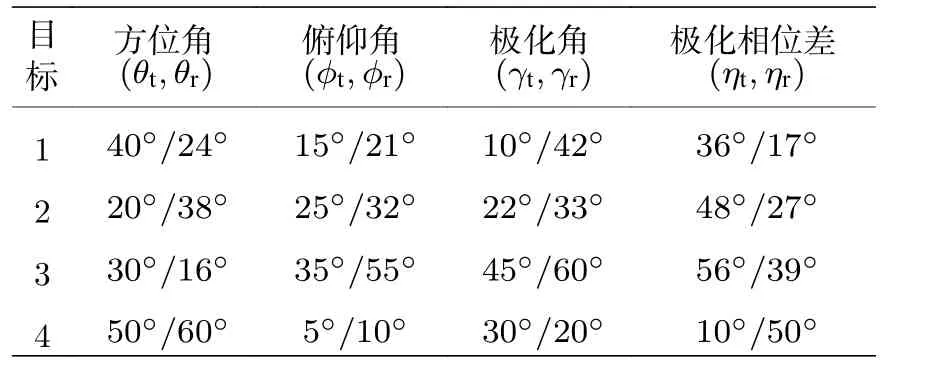
表1 目標回波參數表Table 1.Parameters of target signals.

從圖4(a)和圖4(b)中可以看出, 提出的平行因子算法能夠實現2D-DOD 和2D-DOA 的自動參數配對.同時從圖4(c)—圖4(f)中可以看出, 通過對利用平行因子算法得到的發射加載矩陣和接收加載矩陣進行盲估計算法應用能夠有效地實現發射方位角、發射極化角、發射極化相位差、接收方位角、接收極化角和接收極化相位差的角度參數配對.并且, 在進行四維發射參數和四維接收參數求解時所提出的盲估計算法不需要大電偶極子長度和圓環周長的先驗信息.

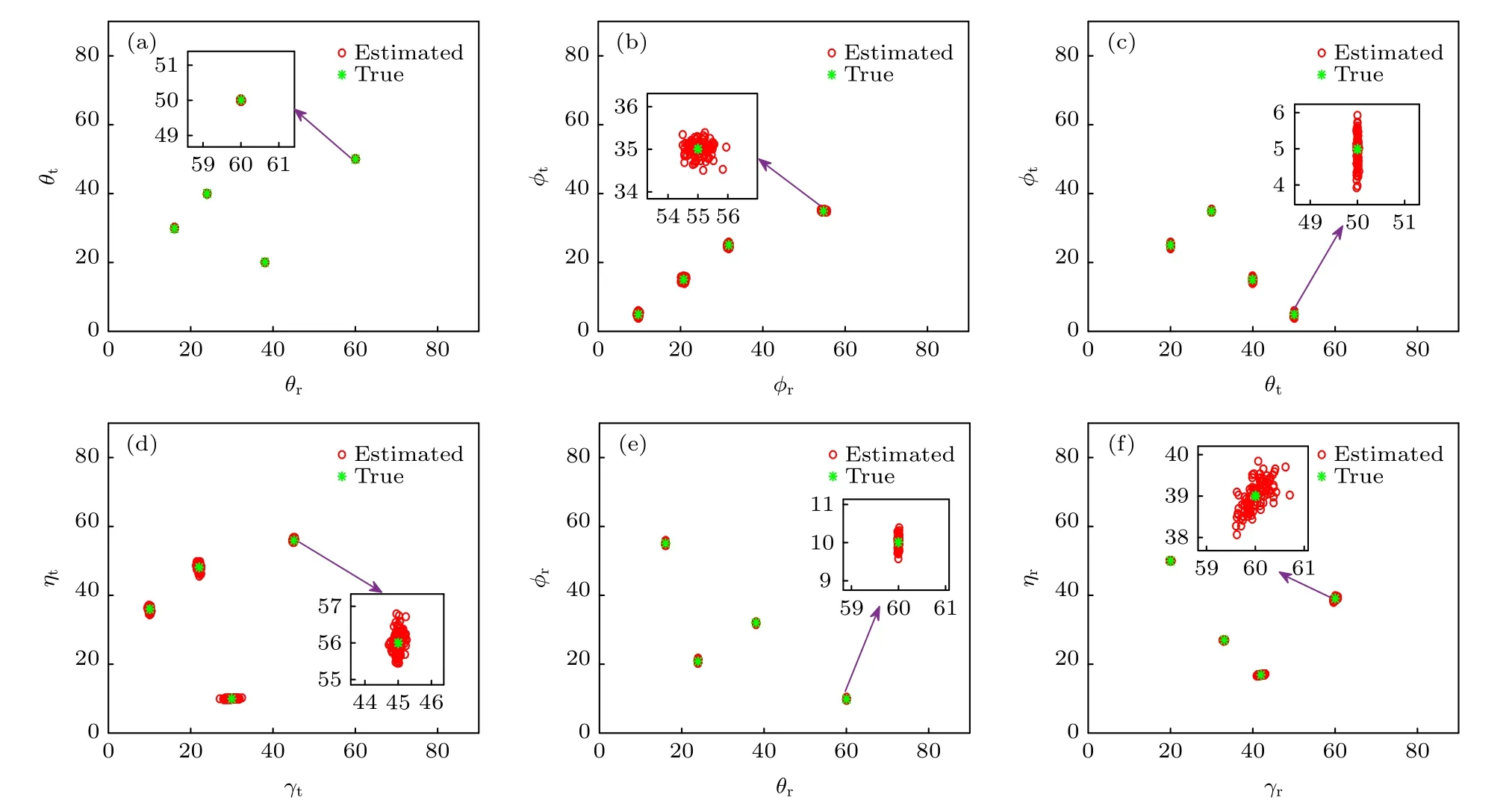
圖4 新型雙基地EMVS-MIMO 雷達角度參數和極化參數估計星座圖 (a) 發射俯仰角和接收俯仰角; (b) 發射方位角和接收方位角; (c) 發射俯仰角和發射方位角; (d) 發射極化角和極化相位差; (e) 接收俯仰角和接收方位角; (f) 接收極化角和極化相位差Fig.4.Scatter plot of the angle parameters and polarization parameters by using the new designed bistatic EMVS-MIMO radar:(a) Scatter plot of the transmit elevation angle and receive elevation angle ; (b) scatter plot of the transmit azimuth angle and receive azimuth angle; (c) scatter plot of the transmit elevation angle and azimuth angle ; (d) scatter plot of the transmit polarization angle and polarization phase difference; (e) scatter plot of the receive elevation angle and azimuth angle ; (f) scatter plot of the receive polarization angle and polarization phase difference.

4.2 長電偶極子和大磁圓環組成的新型EMVS 陣列隨信噪比的變化

在第二個仿真實驗中, 驗證長電偶極子和大磁圓環組成的新型EMVS 陣列的角度和極化參數估計性能隨信噪比的變化.均方誤差的定義為其中表示估計得到的角度或極化參數, ? 表示真實的角度或極化參數,I 表示蒙特卡羅仿真實驗次數.在這個仿真中, 信噪比的變化范圍是 ? 10 — 3 0 dB , 變化的步長為5 dB, 在每個信噪比條件下蒙特卡羅仿真實驗次數為200.同時, 也給出了相應的檢測成功概率曲線.其中檢測成功概率定義為每個入射信源的估計角度和極化角度與真實的角度和極化角度的差值小于 1?.入射信源的個數K 此時設置為3, 相應的發射四維參數和接收四維參數和第一個實驗中前三個入射信源相同.長電偶極子的長度設置為L/λ=0.5 , 大磁圓環的周長設置為 2 π(R/λ)=1.其中的下標d 表示角度參數, 下標p 表示極化參數.圖中 s1d, s2d, s3d和 C RBds1 , C RBds2 ,CRBds3分別對應于第一個信源、第二個信源和第三個信源的角度參數以及相應的克拉美羅界.同樣地, 圖中s1p, s2p, s3p, 和 C RBps1 , C RBps2 , C RBps3 分別對應于第一個信源、第二個信源和第三個信源的極化參數以及相應的克拉美羅界.從圖5 中可以看出, 每個信源的均方誤差性能和檢測成功概率隨著信噪比的增加而提升.通過仿真可以發現, 對于實際中用到的長電偶極子和大磁環組成的EMVS 雙基地MIMO 雷達系統, 通過對電偶極子和磁環周長進行合理的設置, 其相應的角度參數估計精度能夠維持在一個合理的區間.總體上, 在信噪比大于10 dB 之后, 所提出的盲估計算法具有較好的參數估計精度.因此, 圖5 中的仿真實驗結果為進一步利用長電偶極子和大磁圓環組成的新型EMVS 陣列提供了相應的指導.

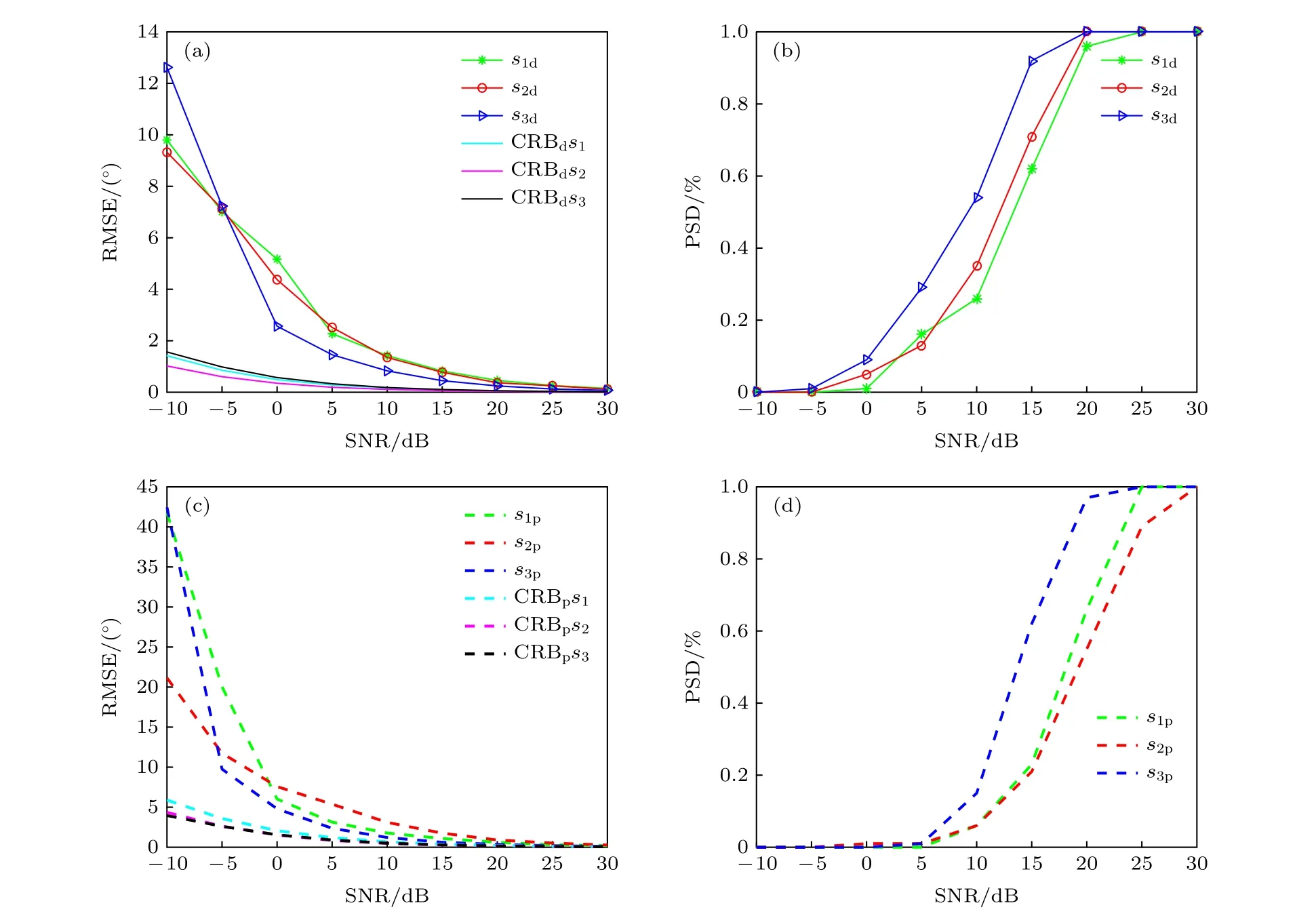
圖5 新型陣列角度和極化參數估計性能隨信噪比的變化 (a) 角度估計均方誤差隨信噪比的變化; (b) 角度檢測概率隨信噪比的變化; (c) 極化估計均方誤差隨信噪比的變化; (d) 極化檢測概率隨信噪比的變化Fig.5.The effect of the SNR for the proposed new bistatic EMVS-MIMO radar: (a) Curves of angle’s RMSE versus SNR; (b) curves of angle’s PSD versus SNR; (c) curves of polarization’s RMSE versus SNR; (d) curves of polarization’s PSD versus SNR.

4.3 長電偶極子和大磁圓環組成的新型EMVS 陣列隨快拍數的變化

在第三個實驗中考慮快拍數對長電偶極子和大磁圓環組成的雙基地EMVS-MIMO 雷達角度參數估計性能的影響.這里, 入射信源的個數以及其相應的發射和接收四維參數和第二個實驗相同.長偶極子的長度和大圓環的周長仍然保持不變.快拍數的變化范圍為 1 00 ?1000 , 變化的步長為100.信噪比設置為 1 0 dB.在每個快拍數條件下蒙特卡羅仿真實驗次數為200.從圖6 中的仿真結果可以看出, 隨著快拍數的增加, 新型EMVS 陣列的角度和極化參數估計性能在提升.但是由于信噪比設置為10 dB, 三個信源最終的檢測成功概率仍然不能接近于1.這說明在該信噪比的條件下, 利用新型陣列結構估計得到的角度參數和極化參數和真實的角度參數和極化參數之間的差值仍然大于所設定的門限值.因此, 為了獲得更加良好的角度和極化參數性能, 在實際的角度參數估計中, 應該設置較高的信噪比門限, 從而提升新型陣列的空間目標獲取能力.

4.4 電偶極子的長度對估計精度的影響

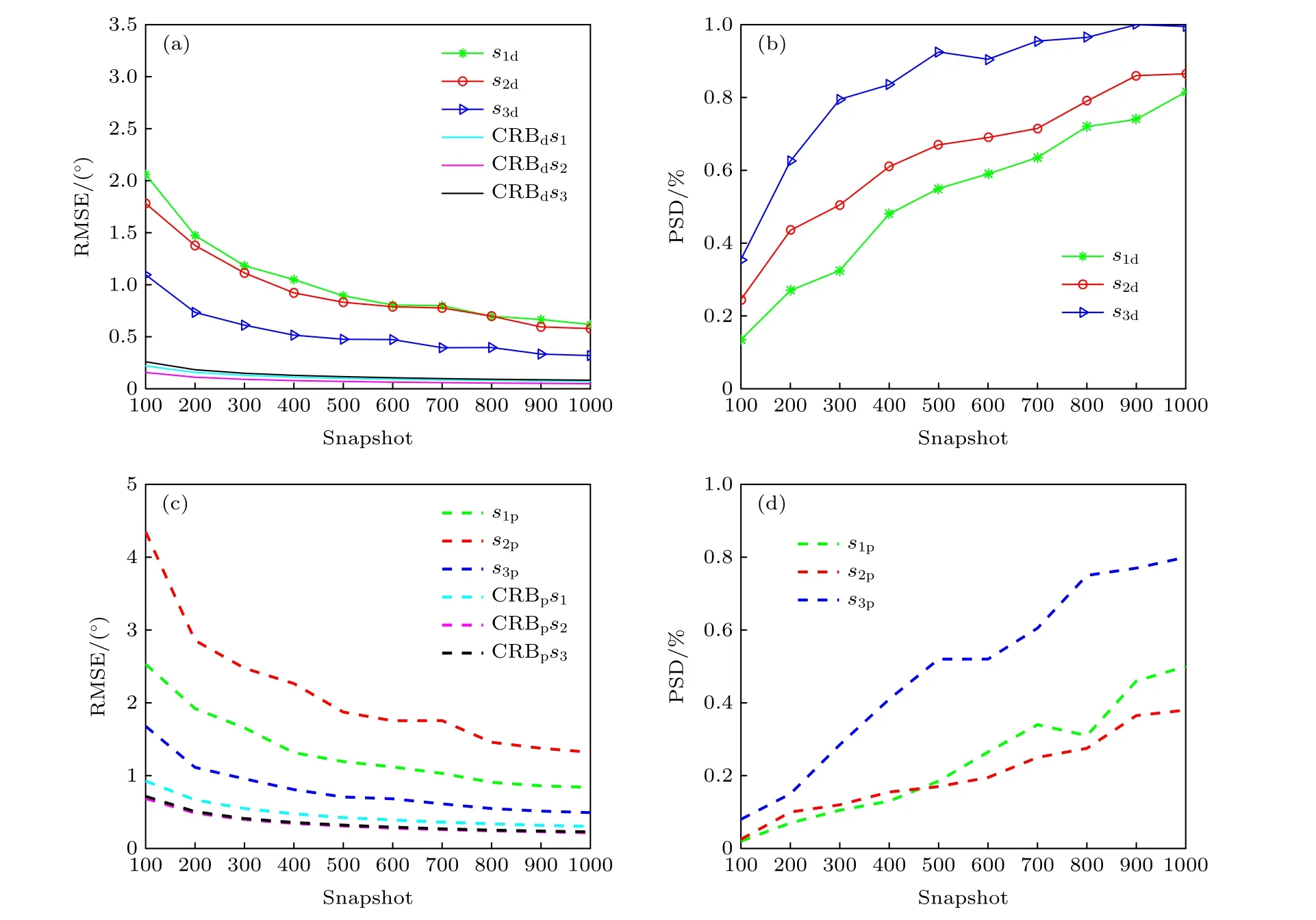
圖6 新型陣列角度和極化參數估計性能隨快拍數的變化 (a) 角度估計均方誤差隨快拍數的變化; (b) 角度檢測概率隨快拍數的變化; (c) 極化估計均方誤差隨快拍數的變化; (d) 極化檢測概率隨快拍數的變化Fig.6.The effect of the snapshot for the proposed new bistatic EMVS-MIMO radar: (a) Curves of angle’s RMSE versus snapshot;(b) curves of angle’s PSD versus snapshot; (c) curves of polarization’s RMSE versus snapshot; (d) curves of polarization’s PSD versus snapshot.

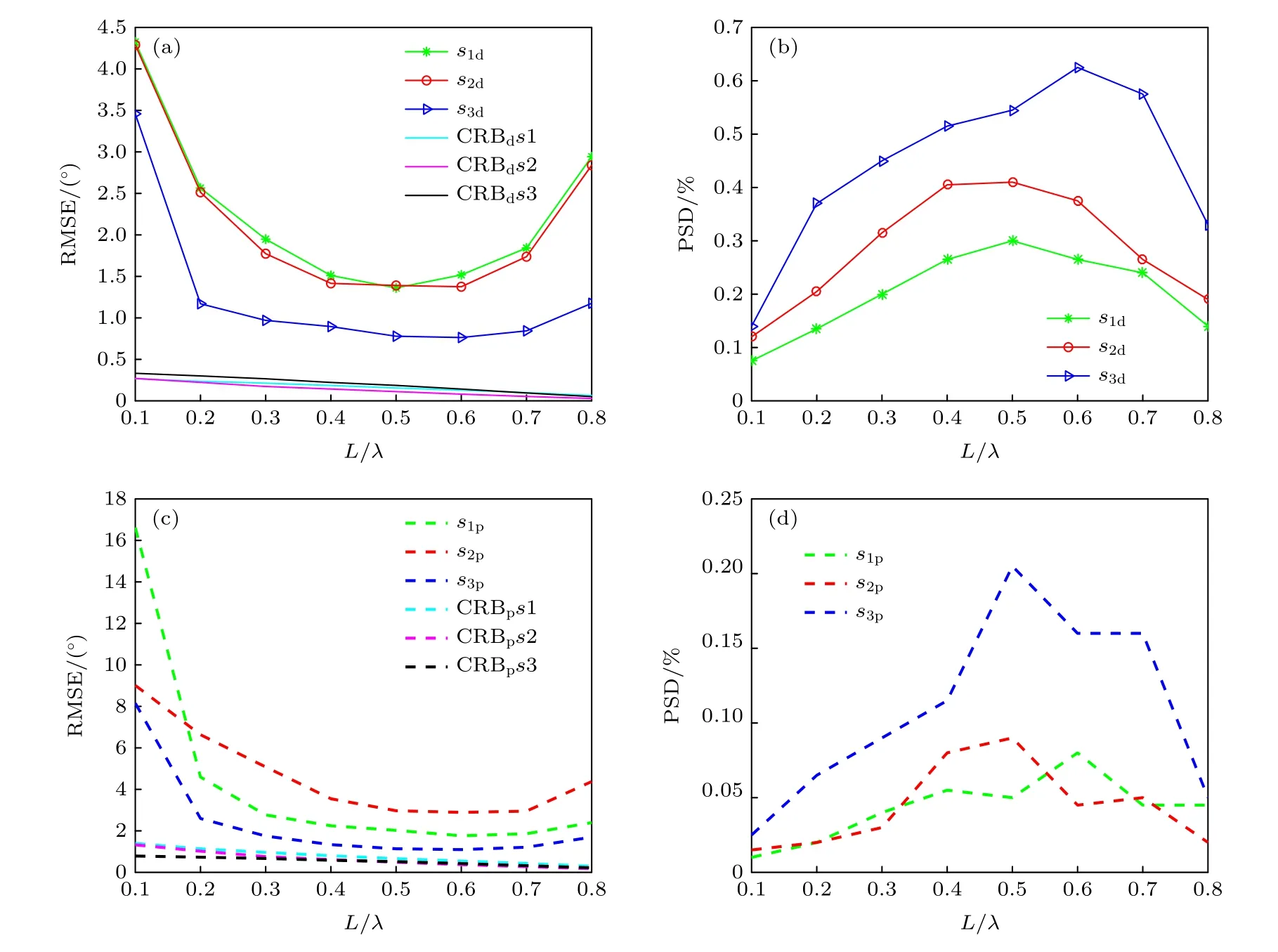
圖7 不同電偶極子的長度對角度和極化參數估計性能的影響 (a) 角度估計均方誤差隨電偶極子長度的變化; (b) 角度檢測概率隨電偶極子長度的變化; (c) 極化估計均方誤差隨電偶極子長度的變化; (d) 極化檢測概率隨電偶極子長度的變化Fig.7.The effect of the various L /λ for the proposed new bistatic EMVS-MIMO radar: (a) Curves of angle’s RMSE versus various L /λ ;(b) curves of angle’s PSD versus various L /λ ; (c) curves of polarization’s RMSE versus various L /λ ; (d) curves of polarization’s PSD versus various L /λ.

在第四個仿真實驗中驗證電偶極子的長度變化對雙基地EMVS-MIMO 雷達中角度和極化參數估計性能的影響, 該仿真實驗結果為設計合適長度的電偶極子提供相應的參考.入射信源的個數及其發射四維參數和接收四維參數和第二個實驗相同.此時, 信噪比和快拍數分別被設置為200 和 1 0 dB.大磁環的周長被設置為 2 π(R/λ)=1.電偶極子的長度的變換范圍是0.1—0.8, 變化步長為0.1.在每個大電偶極子背景下蒙特卡羅仿真實驗次數被設置為200.從圖7 中的仿真結果可以發現, 隨著電偶極子長度的增加, 所設計的新型EMVSMIMO 雷達的角度參數和極化參數估計性能先是變好, 然后又變差.這說明并不是電偶極子的長度越長越好, 越長的電偶極子可能會產生較大的角度和極化參數估計誤差.同時從檢測成功概率曲線可以看出, 隨著電偶極子長度的增加, 對于極化參數具有較低的估計性能.該仿真實驗說明在此信噪比和快拍數的背景下, 長電偶極子的長度變化對極化參數的估計能力較弱.

4.5 磁偶極子的周長對估計精度的影響

最后, 通過仿真實驗來驗證磁偶極子的周長對新型陣列角度和極化參數估計性能的影響.入射信源的個數及其發射四維參數和接收四維參數和第二個實驗相同.此時, 信噪比和快拍數分別被設置為200 和 1 0 dB.長電偶極子的長度被設置為L/λ=0.5.大磁環周長的變換范圍是0.1—2.8, 變化步長為0.3.在每個大磁環周長背景下蒙特卡羅仿真實驗次數被設置為200.從圖8 的仿真結果可以發現, 隨著磁偶極子周長的增加, 所設計的新型EMVS-MIMO 雷達的角度參數和極化參數估計性能并不能一直保持不變.當磁環的周長2π(R/λ)>1時, 新型EMVS 陣列的角度參數和極化參數估計性能隨著磁環周長的增加而變差.對應的檢測成功概率也較差.尤其是對于極化參數的估計性能,其均方誤差還是具有相對較大的值.因此, 在對磁環周長進行設計時, 不能一味地追求輻射效率而忽視角度參數估計精度.通過第四個和第五個實驗,在進行長電偶極長度和大磁環周長設計時, 即要兼顧輻射效率也要兼顧角度參數估計精度, 在二者之間尋求一個較好的平衡點.

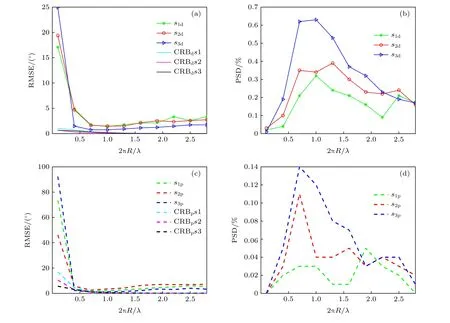
圖8 不同磁偶極子周長對角度參數和極化參數估計性能的影響 (a) 角度估計均方誤差隨磁偶極子周長的變化; (b) 角度檢測概率隨磁偶極子周長的變化; (c) 極化估計均方誤差隨磁偶極子周長的變化; (d) 極化檢測概率隨磁偶極子周長的變化Fig.8.The effect of the various 2 π(R/λ) for the proposed new bistatic EMVS-MIMO radar: (a) Curves of angle’s RMSE versus various 2 π(R/λ) ; (b) curves of angle’s PSD versus various 2 π(R/λ) ; (c) curves of polarization’s RMSE versus various 2 π(R/λ) ;(d) curves of polarization’s PSD versus various 2 π(R/λ).

5 結 論

為了解決實際中短電偶極子和小磁環在雙基地MIMO 雷達中輻射效率不足的問題, 本文利用長電偶極子和大圓磁環來設計新型的發射EMVS陣列和接收EMVS 陣列來處理實際中雙基地MIMO雷達的角度參數和極化參數估計問題.在進行角度和極化參數求解的過程中, 通過采用平行因子算法來實現對陣列接收數據三維結構的利用和發射俯仰角和接收俯仰角的角度參數配對.同時, 由于歸一化坡印亭矢量估計器無法實現長電偶極子和大圓磁環組成的新型EMVS 陣列中的角度和極化參數的提取, 新的盲估計算法被提出來實現對發射四維參數和接收四維參數進行有效估計.所提出的盲估計算法能夠實現發射方位角、發射極化角、發射極化相位差、接收方位角、接收極化角、接收極化相位差和發射俯仰角、接收俯仰角的自動參數配對.通過理論分析和仿真實驗可以發現, 在實際應用中并不是電偶極子的長度和磁環的周長越大越好, 在對電磁矢量傳感器進行設計時, 既要考慮輻射效率也要考慮角度參數的估計精度.因此, 本文針對長電偶極子和大磁圓環背景下的雙基地MIMO 雷達的研究能夠為下一步的工程應用提供相應的參考.

附錄A

為了實現Fisher 信息矩陣 J 中各個元素的求解, 下面首先詳細分析協方差矩陣 R 關于 ( θt,?t,γt,ηt,L,R) 和(θr,?r,γr,ηr,L,R)偏導數的具體形式

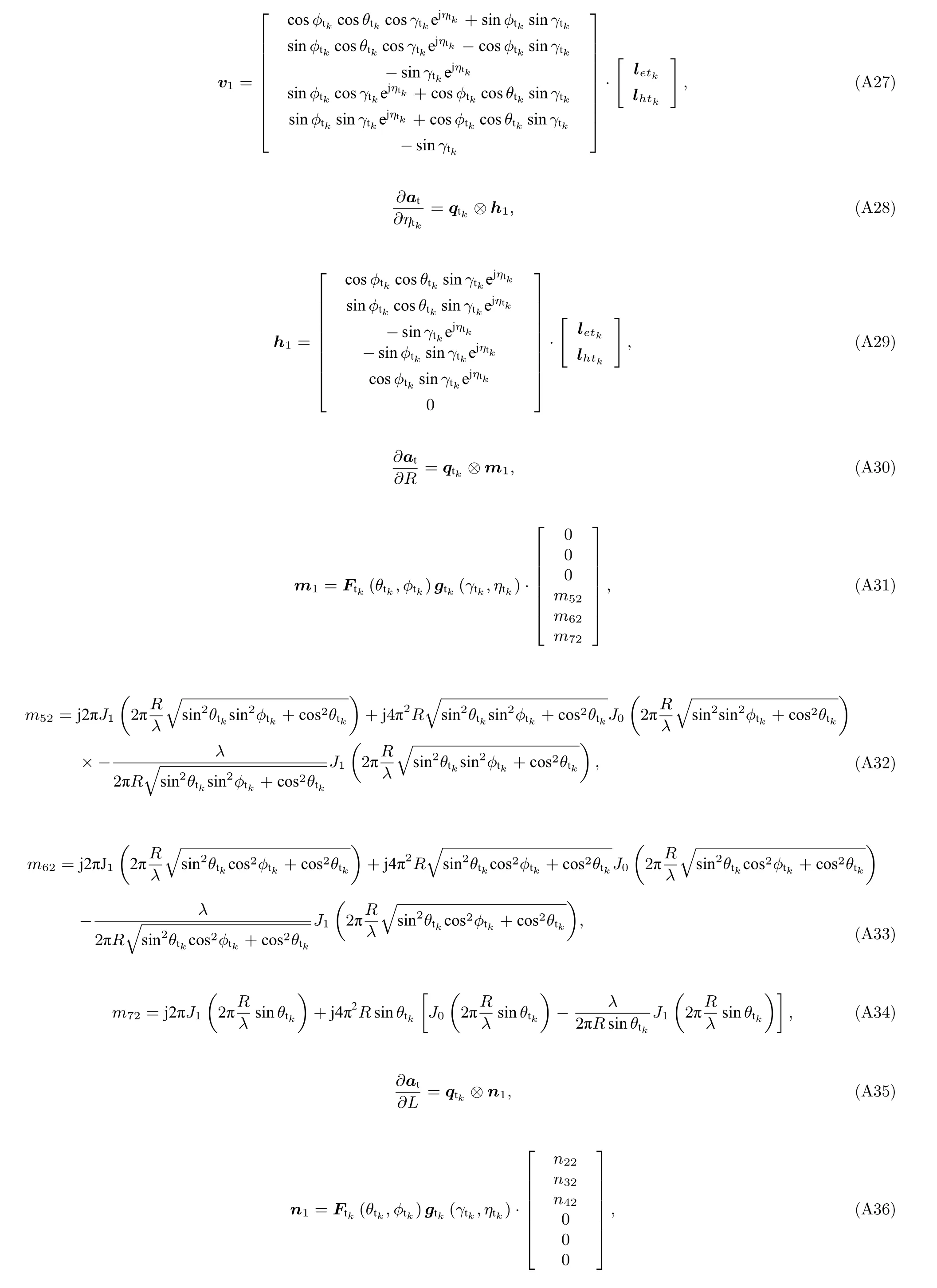
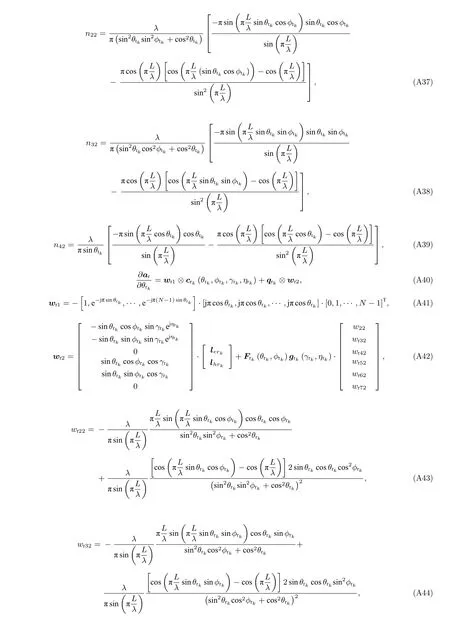
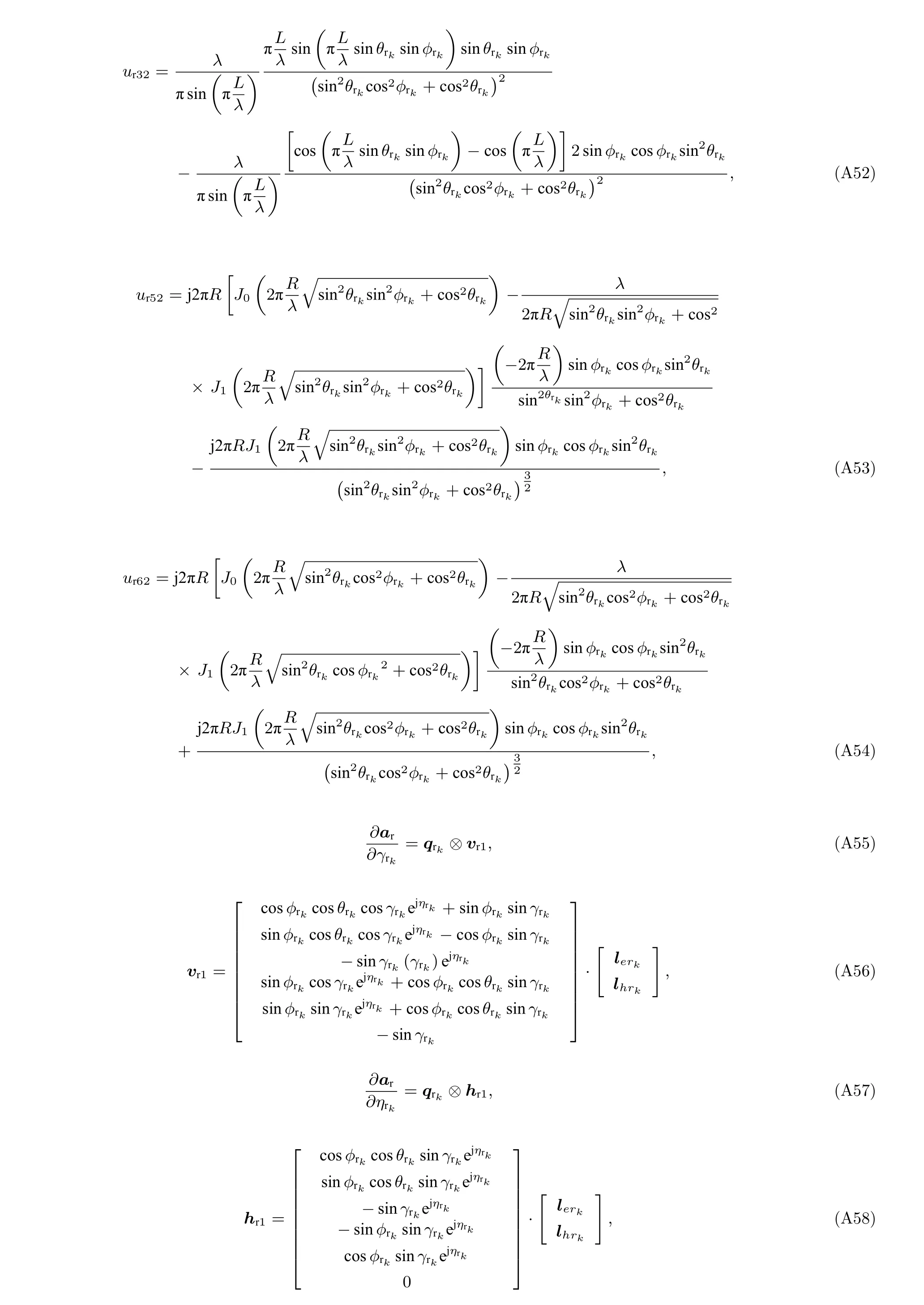
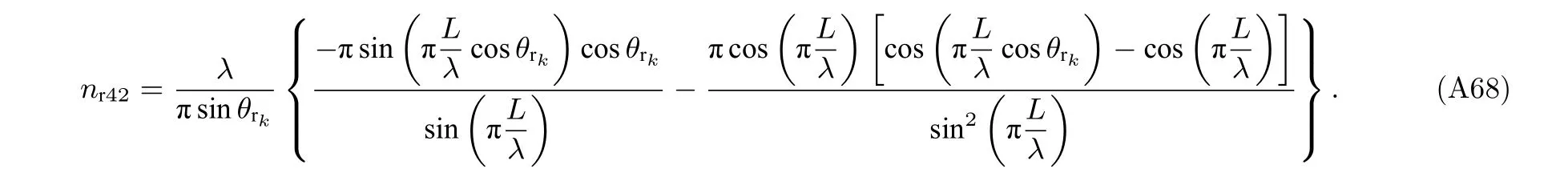
根據以上公式， Jθtθt(i,j) 可以被表示為

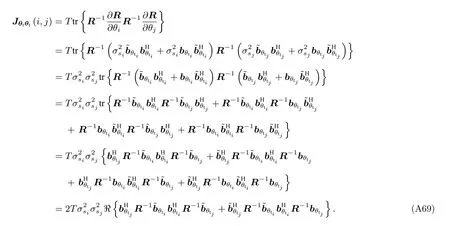
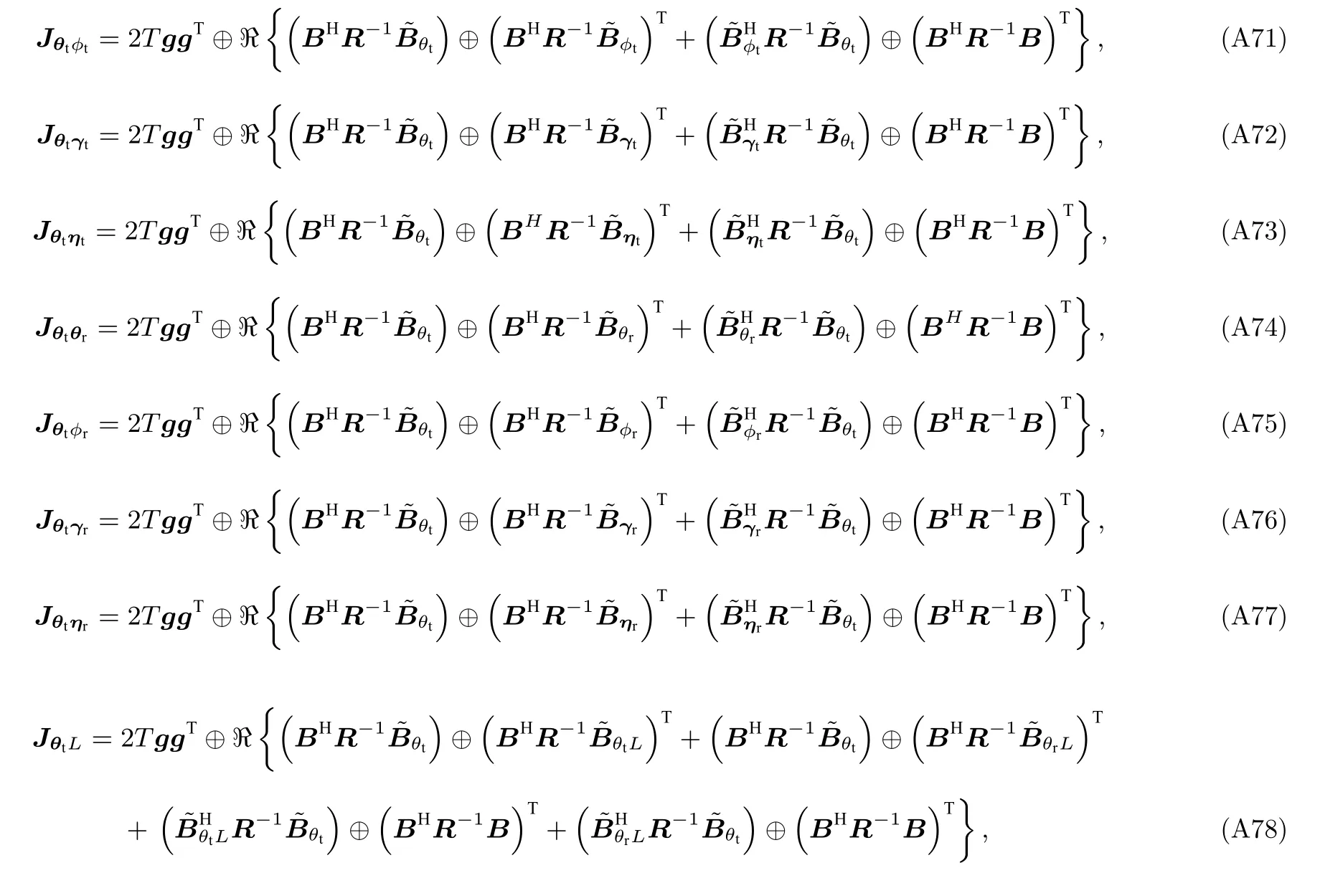
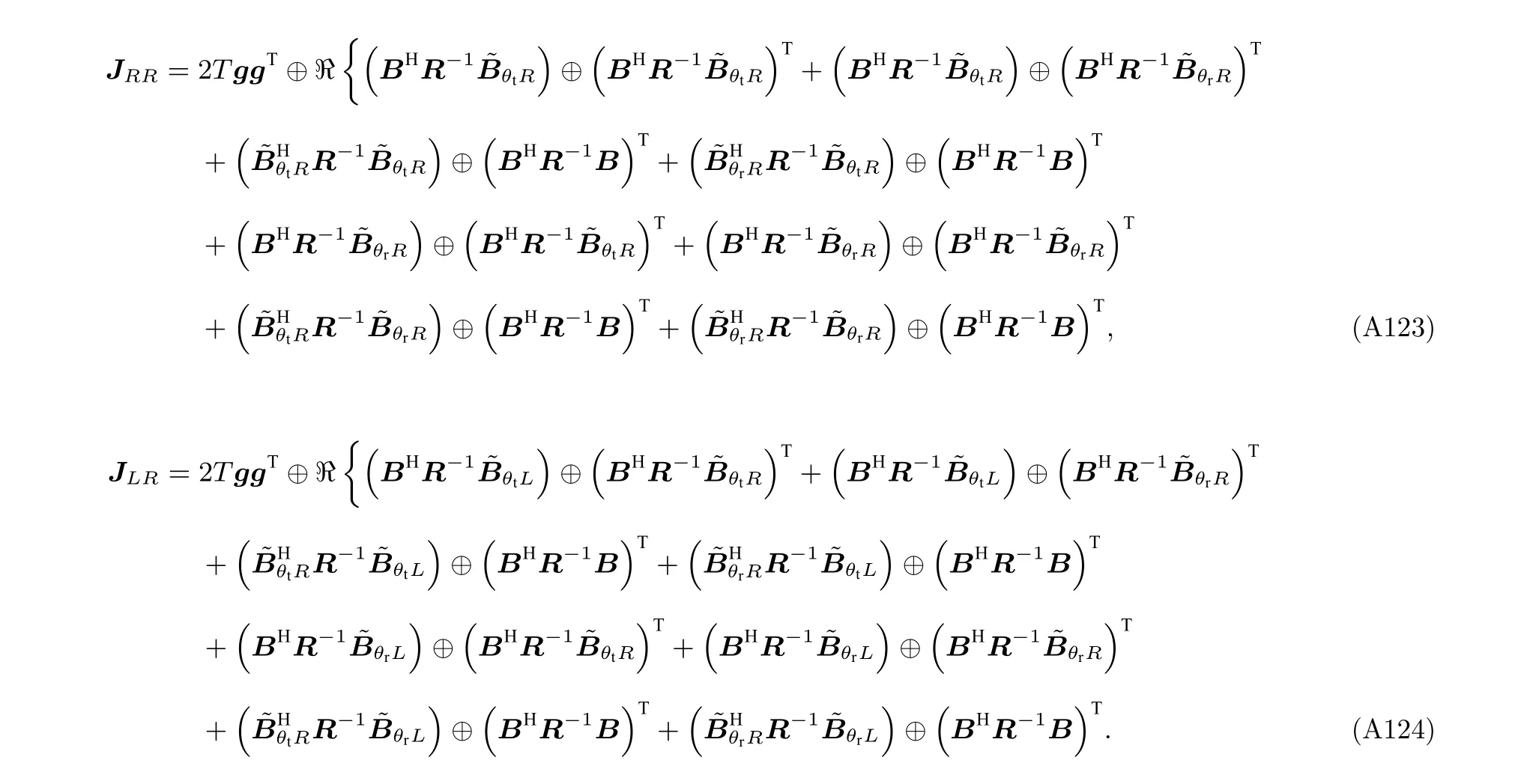
經過以上的詳細推導過程即可實現Fisher 信息矩陣 J 中各個元素的求解.