車路協同下基于沖突規避的匝道合流優化控制方法

陳潤超

(廈門市城市規劃設計研究院有限公司 廈門 361012)

駛入匝道瓶頸的匯入行為是強制性換道行為，瓶頸點是快速路連續流交通設施的咽喉，駕駛員的換道行為是觸發瓶頸失效的因素之一。減少匝道合流過程中的沖突、控制匝道車輛匯入過程的換道行為有利于瓶頸區域的車輛有序行駛。而車路協同技術(cooperative vehicle infrastructure system, CVIS)為車輛合流過程的沖突識別及駕駛員換道行為指導提供了技術支持。

CVIS環境下的匝道控制方法研究一直受到學者們的關注。文獻[1]以車輛的燃油經濟性最優為目標提出了合流區智能車輛集中控制的方法。文獻[2]考慮了主線車速調節和車輛換道因素，提出基于車路協同的匝道車輛匯入引導方法。文獻[3]提出了一種車聯網環境下的交叉口沖突管理算法。文獻[4]針對匝道合流區搭建了智能網聯車輛控制方案并驗證了方案的有效性。文獻[5]以車輛油耗和行程時間最優為目標提出了一種匝道合流的自動駕駛車輛協調方法。從現有的研究來看，主要集中主道和匝道車輛間隙的關系，對于沖突管理的角度考慮較少。

本文通過分析匝道合流區域的車輛合流過程，以沖突規避為原則，提出了一種CVIS環境下的匝道合流優化控制方法，以期降低合流區的沖突，避免車輛在合流過程中走停帶來的安全隱患。

1 沖突規避方法

圖1為車輛合流場景，主道和匝道交叉的區域稱為合流區。匝道車輛在合流區向主道匯入，匯入的過程中與主道車輛可能會存在沖突。

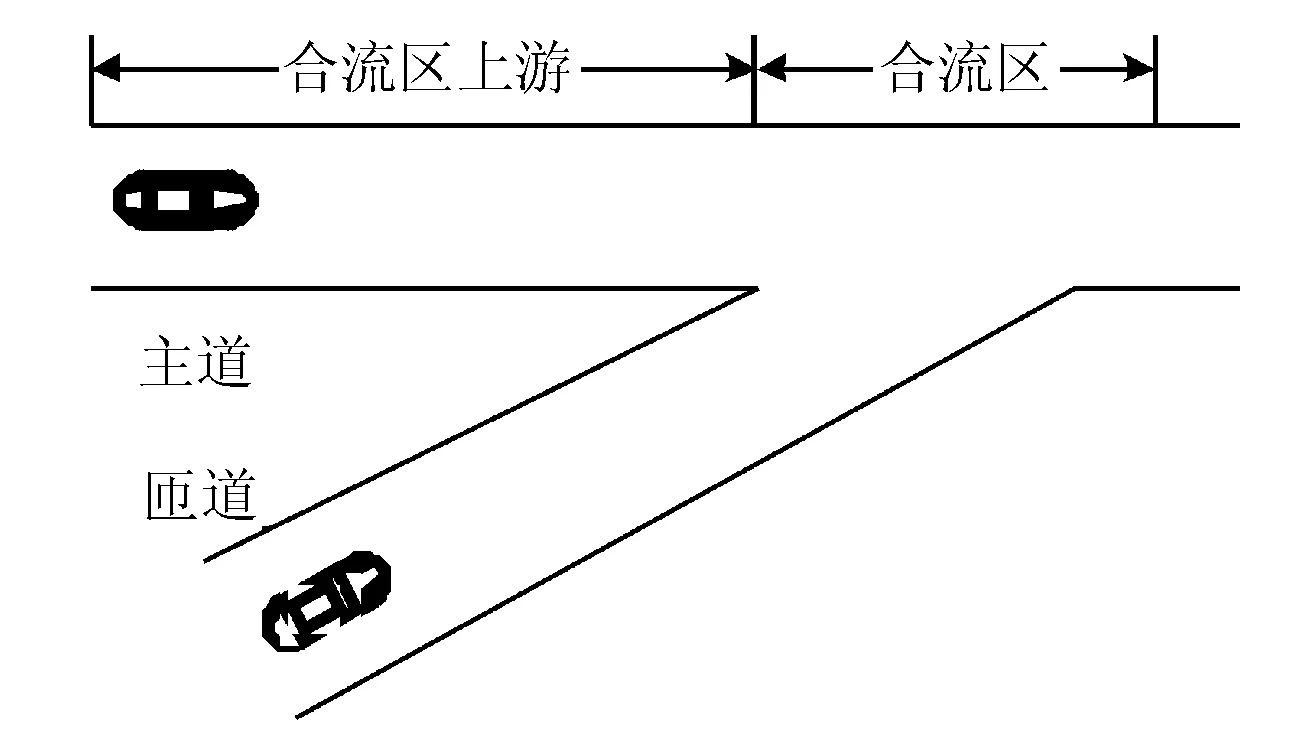
圖1 車輛合流場景

按照先到先服務的原則，智能車輛需要調節自身車輛的加速度以順利依次通過合流區，降低發生沖突的風險。圖2為車輛在合流時空軌跡圖，假設合流區上游的車輛通過合流區的運行軌跡見圖2，xi(t)為車輛隨時間變化的軌跡,ti(o)為車輛i到達沖突區的時間，ti(d)為車道離開沖突區域的時間。其中車輛的速度為vi，加速度為ai，以車輛i為例，在經歷了t時間后距離車輛起始位置的位移計算方法見式(1)。

xi(t)=xi(0)-0.5ait2-vi(t)

(1)

式中：xi(0)為t=0時車輛i的初始位置。

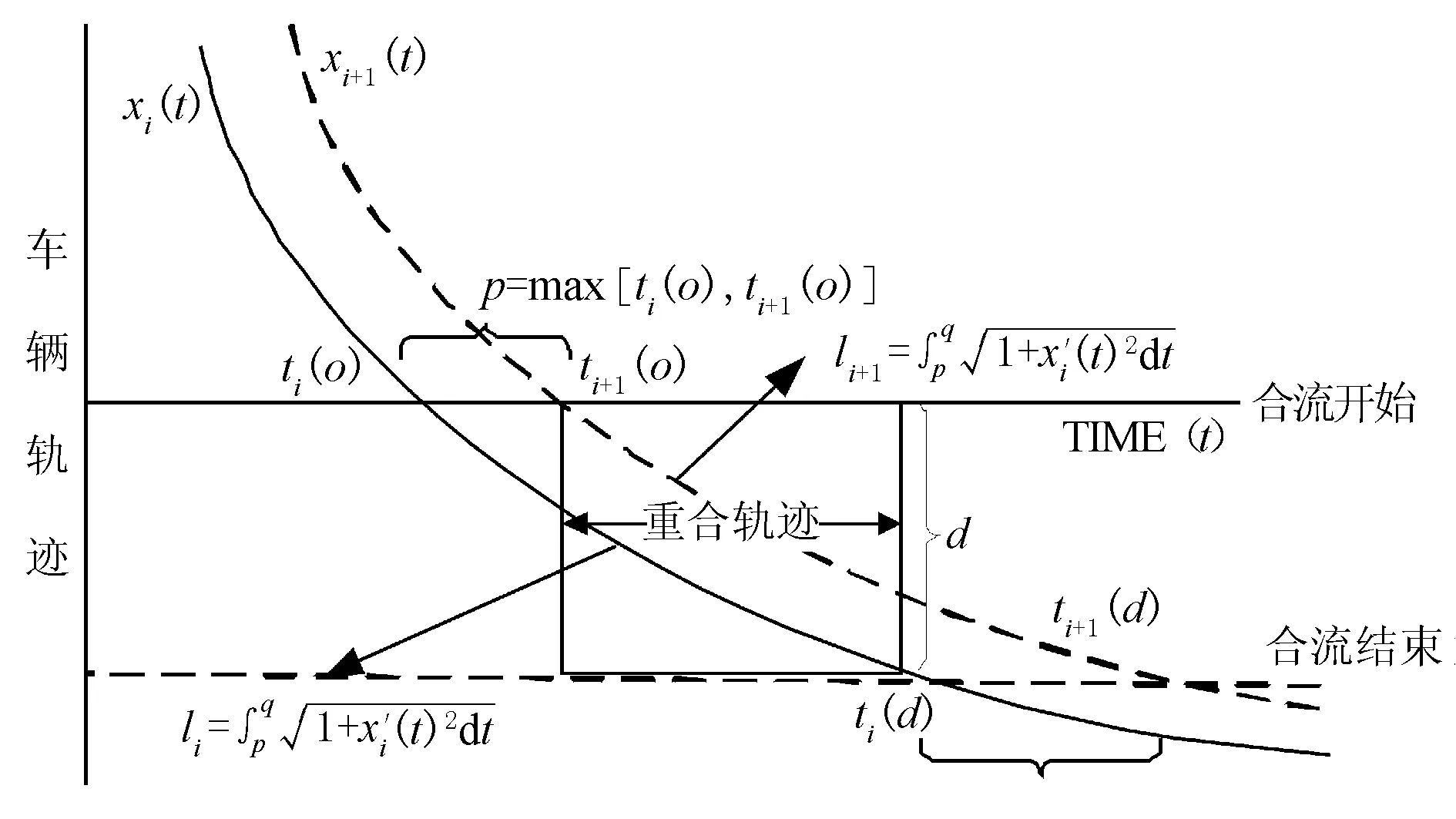
圖2 車輛在合流區的時空軌跡圖

p為車輛i與i+1到達匝道合流區的最晚時間；q為車輛與離開匝道合流區的最早時間；li與li+1分別為車輛i與i+1在重疊區域的曲線長度。如果p>q，則li與li+1不存在，兩車不會同時出現在合流沖突區，也就沒有發生沖突的可能。因此，車輛在匝道合流區域的時空軌跡重疊越小，處于合流區域的車輛就越不容易發生事故，車輛也就越安全。車輛i重合的軌跡長度l的計算方法見式(2)。

(2)

因此，可以把匝道合流區域內車輛的安全協作問題轉化為合流區域內時空軌跡圖的曲線長度問題。

2 基于沖突規避的車輛控制方法

2.1 控制場景搭建

CVIS環境下車輛合流過程見圖3。

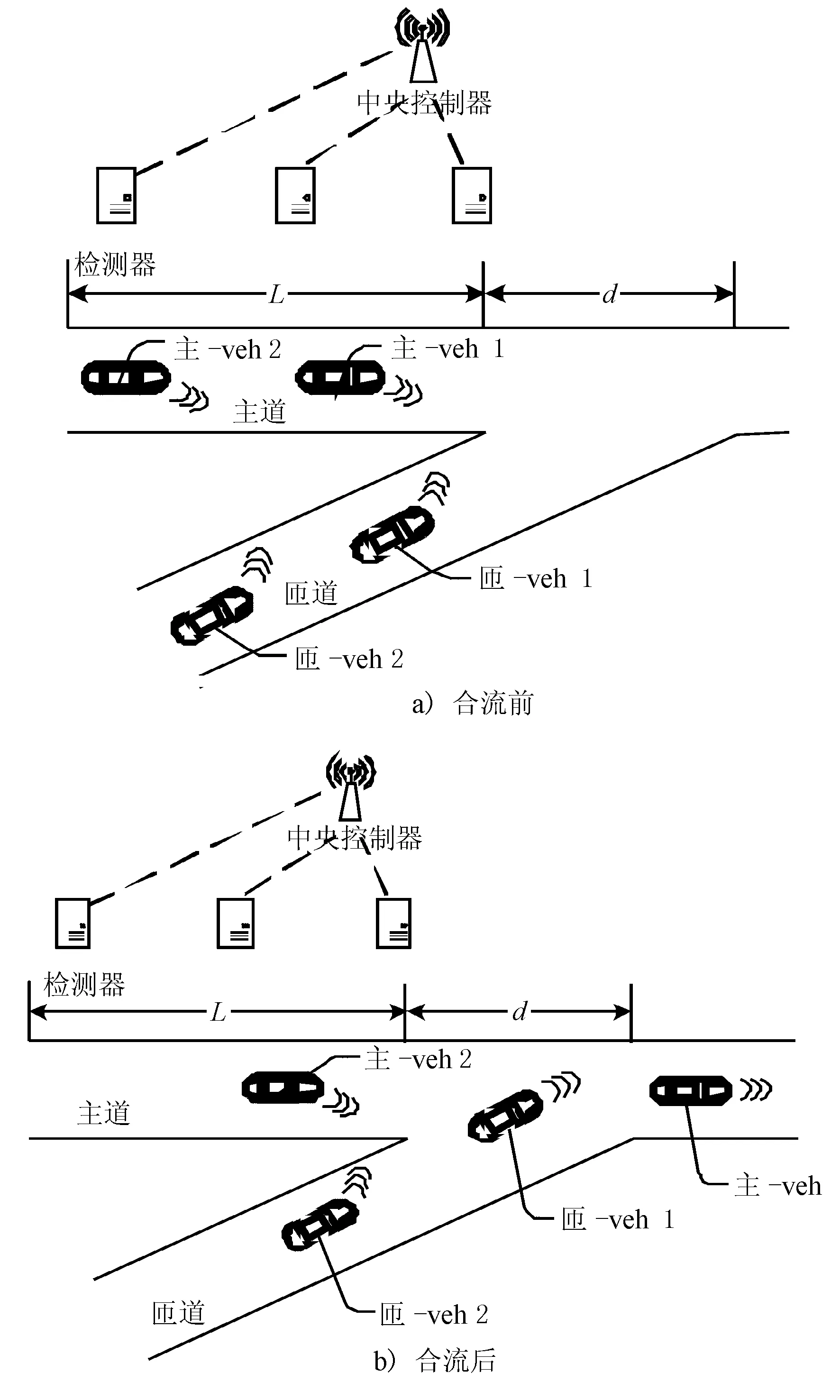
圖3 CVIS環境下車輛合流過程

由圖3可見，合流區長度為d，合流控制范圍為合流區上游長度為L的區域。傳統合流路段的車輛通行是受信號燈或交通標識控制的，這就意味著合流的其中一方必須停車等待，而后才能通行。在CVIS環境下，路側檢測器收集周圍車輛的行駛信息(包括車輛位置、速度、加速度)，發送至中央控制器處理，中央控制器將后續的行車指令發送給相應車輛，實現主道和匝道車輛的協同合流。

2.2 車輛動力學模型

車輛運動學方程為

設T為離散時間的1個步長，則得到離散化的車輛運動學模型如下。

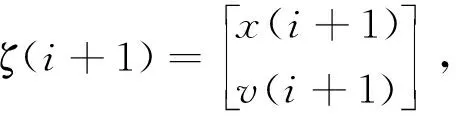
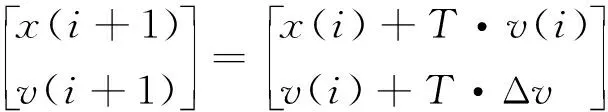
式中：Δv為車輛的加速度；x(i)為第i個時間步的車輛位移；v(i)為第i個時間步的車輛速度。

2.3 車輛合流的優化控制模型

2.3.1控制目標

在匝道合流過程中，控制的目標為合流區的車輛軌跡重合最小，即

式中：m,n分別指主道和匝道的車輛，m=1,2,…,M;n=1,2,…,N；ti指第i個時間步；x為車輛的軌跡的微分，即車輛速度。

2.3.2約束條件

1) 車輛間安全間距約束。

xk(ti)-xk-1(ti)≥G,k=m,n

式中：G為車輛行駛最小安全距離。

2) 車輛行駛速度約束。

0≤vk(ti)≤vmax,k=m,n

式中：vm(ti)、vn(ti)分別為第i個時間步的主道車輛m和匝道車輛n的速度。

3) 對車輛的運動過程進行離散化處理，主道、匝道車輛的位移約束如下。

式中：to,m、to,n分別為主道和匝道車輛進入合流區的時間；td,m、td,n分別為主道和匝道車輛離開合流區的時間；xm(t0)、xn(t0)為在初始時刻t0時，車輛m、n距離合流區起始點的橫向位移；d為合流區的長度。

3 匝道合流優化控制仿真分析

3.1 控制參數設置

初始狀態。

xm2(t0)=-100 m，xm1(t0)=-80 m；

xn2(t0)=-100 m，xn1(t0)=-80 m

所有車輛的初始速度均為5 m/s，初始加速度為0 m/s，d=20 m，G=10 m，vmax=8 m/s。

3.2 控制結果分析

通過對優化控制策略進行數值模擬，優化控制后行駛隊列效果見圖4，優化合流位移效果見圖5。

圖4 優化控制后行駛隊列

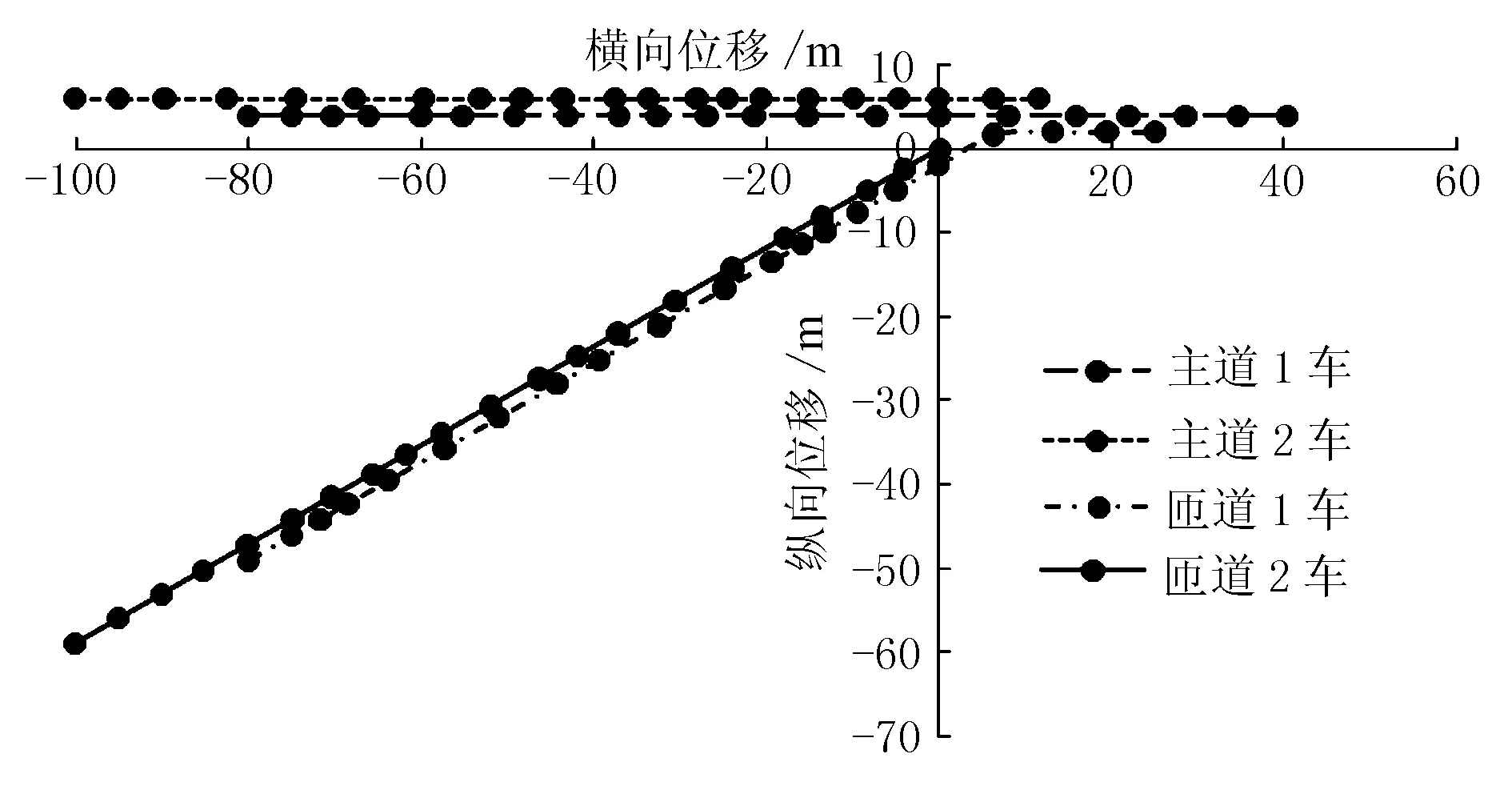
圖5 車輛優化合流位移

由圖5可知，在優化控制過程中，車輛軌跡比較分散，整個合流過程車輛間距均能保持10 m左右,最后在主道上能夠使車輛實現較均勻排列行駛。表明在優化控制算法下，車輛可以按照一定的順序合流，能夠比較充分地利用道路資源，避免合流時車輛間沖突。

3.3 仿真驗證

為驗證控制策略的效果，數值模擬無控制下的合流過程，設置對照組。其參數設置和初始條件不變。

對照組車輛的合流位移見圖6。

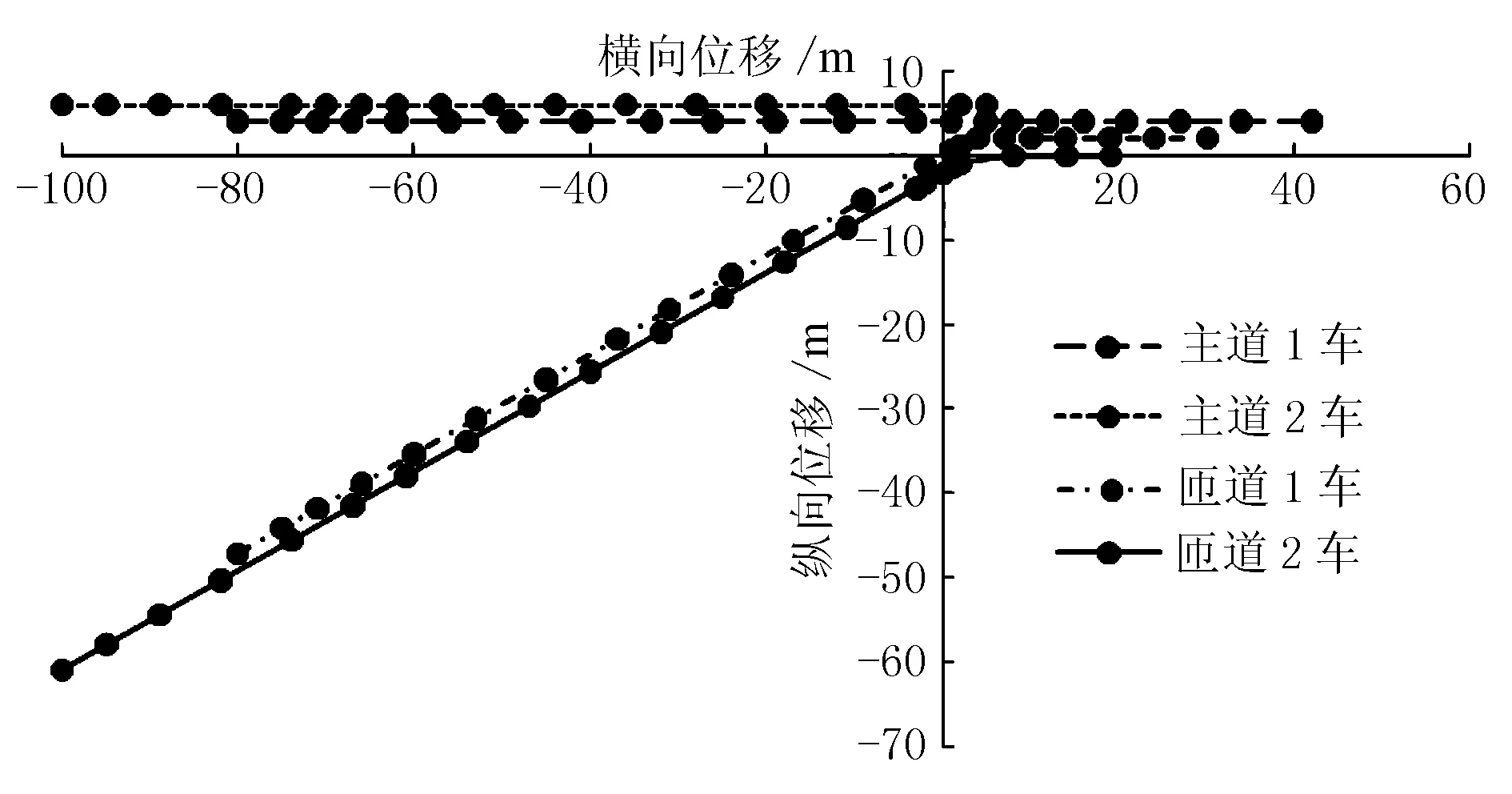
圖6 對照組車輛的合流位移

由圖6可知，在不控制情況下，車輛進入合流上游，其運行軌跡較為分散，靠近合流區時，車輛的運行軌跡較為密集，合流完成后，車輛排成一列繼續行駛。整個過程中，車輛間距離保持在安全范圍。表明在不控制條件下，車輛仍可完成合流，但是在合流區附近，車輛會發生擁擠，甚至停車等待。

為進一步比較不同條件下的車輛運行效果，選取2組仿真過程中所有車輛的平均速度、速度標準差和加速度標準差進行對比分析。

控制組和對照組的車輛速度、加速度圖見圖7，車輛仿真指標表見表1。

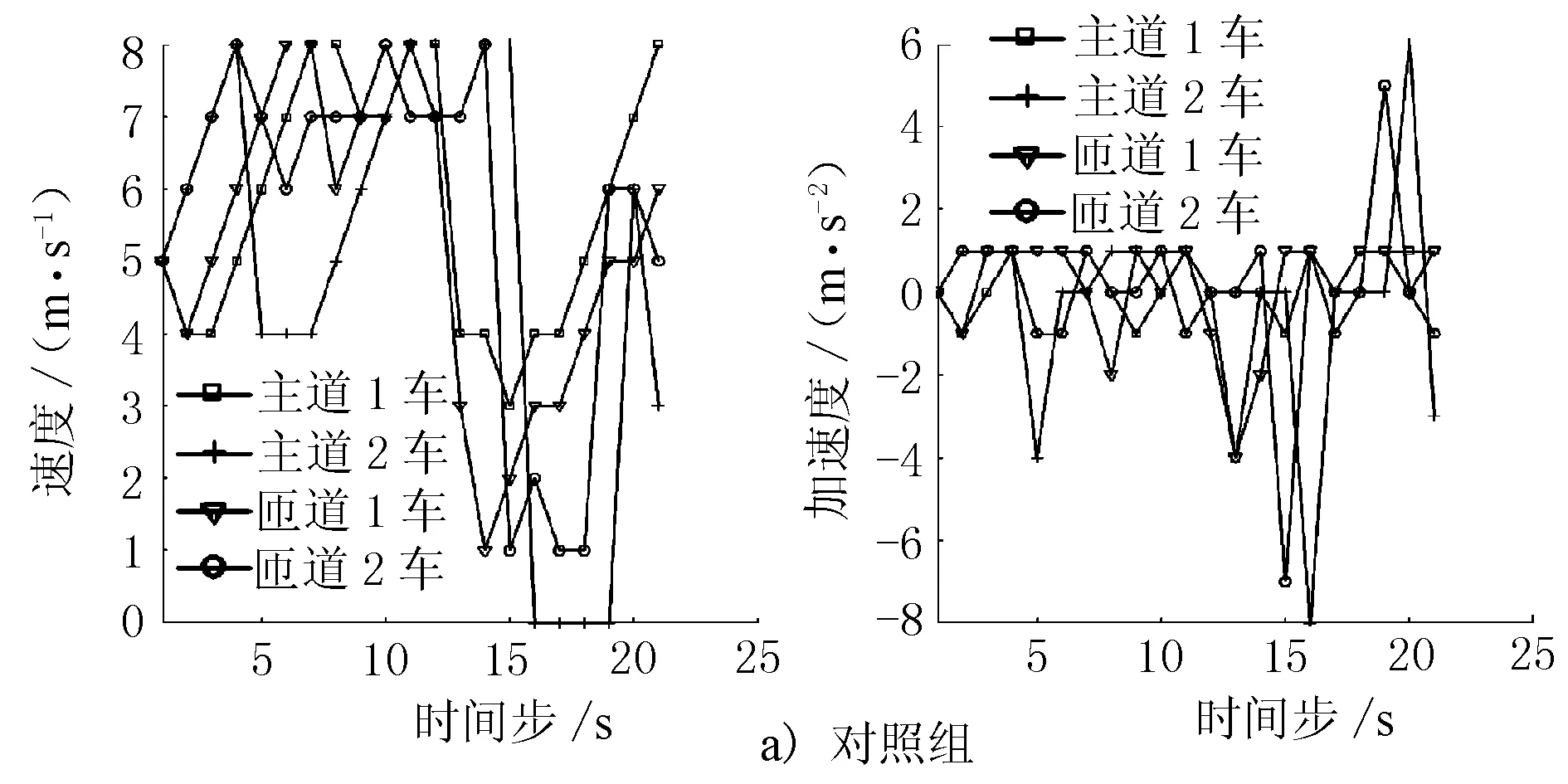
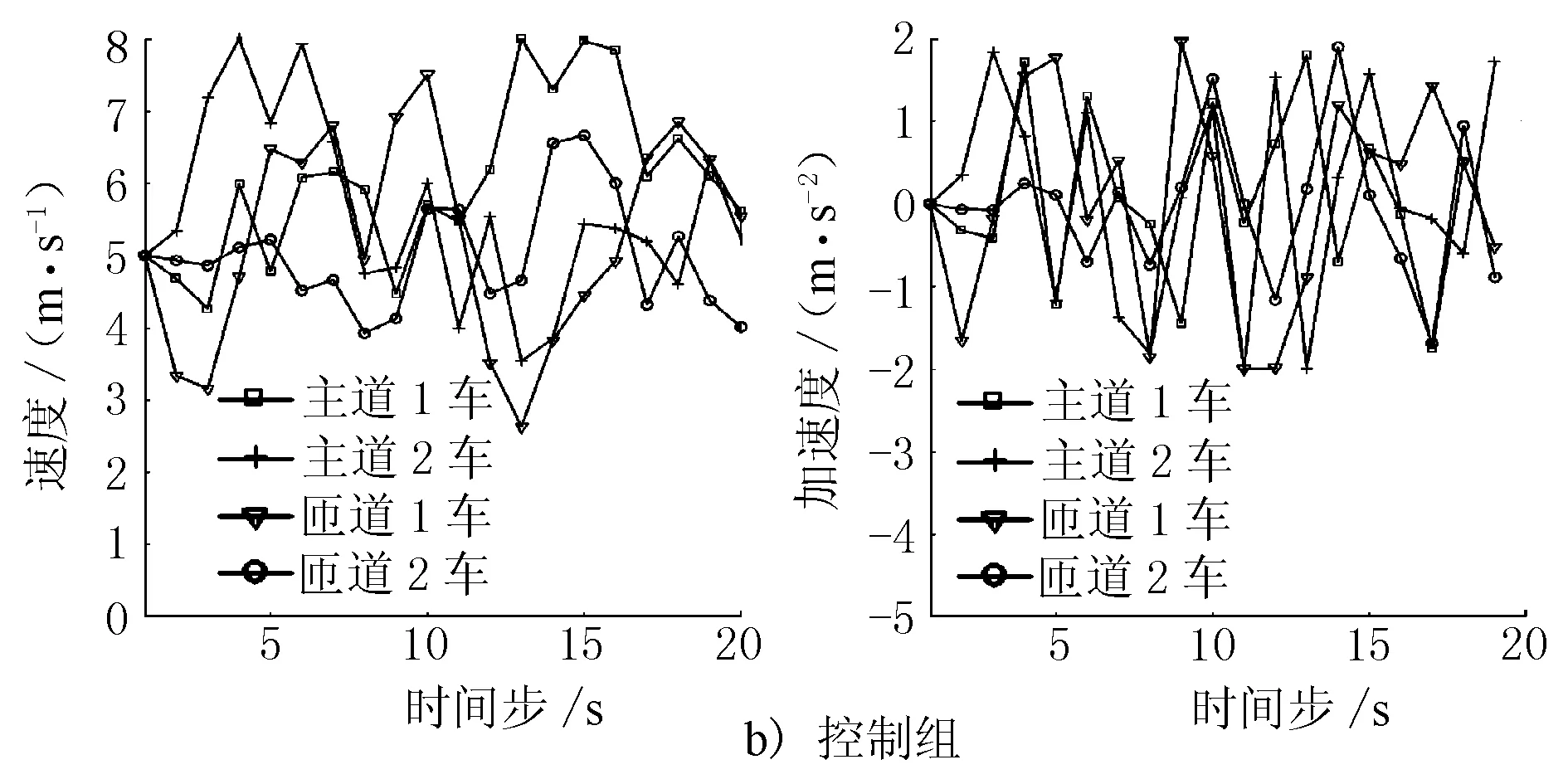
圖7 車輛速度和加速度

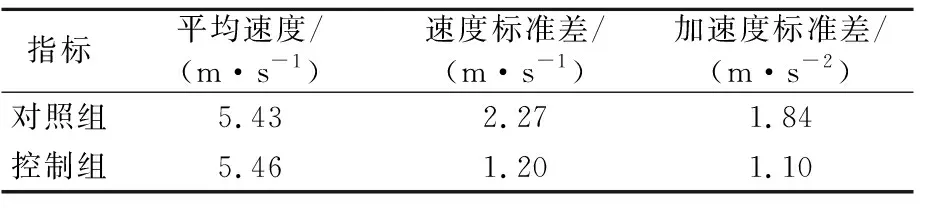
表1 車輛仿真指標

由圖7及表1可知，2組平均速度基本相同，這表明實施控制策略不會降低合流區車輛的運行速度；速度標準差方面，對照組的車輛速度波動較大，為2.27 m/s，特別是靠近合流區附近，而控制組的車輛速度波動較小，運行相對平穩，為1.2 m/s，表明實施控制策略有利于平穩車輛速度，降低車流的波動；且由加速度標準差可見，對照組的車輛加速度在合流區附近波動較大，為1.84 m/s2，控制組車輛的加速度維持在-2～2 m/s2區間，為1.10 m/s2，表明實施控制策略能夠增強車輛行駛的舒適性，不會出現突然加速和急停的情況。

4 結語

本文以匝道合流區為研究對象，根據合流區的特性，以沖突最小為目標，構建了匝道合流區優化控制模型，并進行了數值仿真，表明本文的控制方法能夠使得車輛在避免沖突的前提下順利合流。隨后將其與無控制匝道合流進行對比，以車輛平均速度、速度標準差、加速度標準差為指標進行評價分析，發現控制策略下車流更加穩定，車輛行駛的舒適性、安全性有所提高，表明匝道合流優化控制方法具有一定的現實意義。

本文在研究過程中將匝道合流區的合流情況有所簡化，一些問題仍需進一步的研究。比如，討論更多車輛的合流情況，多車輛合流沖突會增多，也許會更加凸顯優化控制的優勢；另外在合流過程中多車道間車輛的換道過程本文也未討論。