基于雙殘差卷積網絡的低照度圖像增強

陳清江， 屈 梅

(西安建筑科技大學 理學院，陜西 西安710055)

1 引 言

在低照度環境下拍攝的圖像常存在曝光不足以及對比度低的問題，給后續圖像處理帶來嚴峻的挑戰，因此低照度圖像增強已經成為計算機視覺領域的一個研究熱點。近年來，基于直方圖的方法以及由LAND[1]提出的Retinex理論模型在低照度圖像增強領域取得了重大突破，如Pizer等人[2]和Reza等人[3]先后提出AHE算法和CLAHE算法增強低照度圖像，但增強后的圖像往往會出現顏色失真現象。Jobson等人[4]利用高斯平滑函數估計原圖像的亮度分量，提出單尺度Retinex(SSR)方法。LIN等人[5]將多個不同尺度的SSR線性加權求和，提出多尺度Retinex(MSRCR)方法。Fu等人[6]提出了一種基于融合的單背光低照度圖像增強算法。Ying等人[7]提出了一種雙曝光融合算法，以提高精確的對比度和亮度增強，從而實現低照度圖像增強。Ren等人[8]提出基于Retinex模型的弱光圖像聯合去噪與增強算法。雖然以上方法在低照度圖像增強領域取得了很大的進展，但增強后的圖像，亮度恢復不夠，容易造成圖像的細節丟失，仍有一定的局限性。

最近，隨著深度學習的快速發展，深度學習在目標識別[9-12]、超分辨率重建[13-14]以及圖像去雨[15-16]等方面取得優于傳統算法的效果。一些學者也將深度學習應用于圖像增強領域，如Li等人[17]通過將淺層的Lightennet網絡和Retinex模型結合，實現低照度圖像增強；Ma等人[18]提出深度卷積神經網絡(DCNN)實現低照度圖像增強，從而獲得增強后的圖像。

本文提出一種與以往通過估計低照度圖像中照度分量，或將RGB圖像轉換到其他顏色空間不同的預處理的分解方法。將RGB圖像分解在R、G和B三個分量上，通過不同尺度卷積分別提取各分量的特征信息，分別使用雙殘差模塊進行訓練，重建后獲得增強的R、G和B三個分量的圖像，進而得到增強后的RGB圖像。最終，采用雙邊濾波對其進一步優化。

2 Retinex 理論模型

Retinex 理論模型是LAND[1]提出的色感一致性模型，該模型認為人眼觀察到的圖像是光照圖像和反射率圖像的乘積。該模型可表示為：

S(x,y)=L(x,y)R(x,y)，

(1)

式中：(x,y)表示像素的空間二維坐標，S(x,y)表示觀察到的圖像，L(x,y)表示照度分量，R(x,y)表示本身的反射分量。

Retinex模型圖如圖1所示。

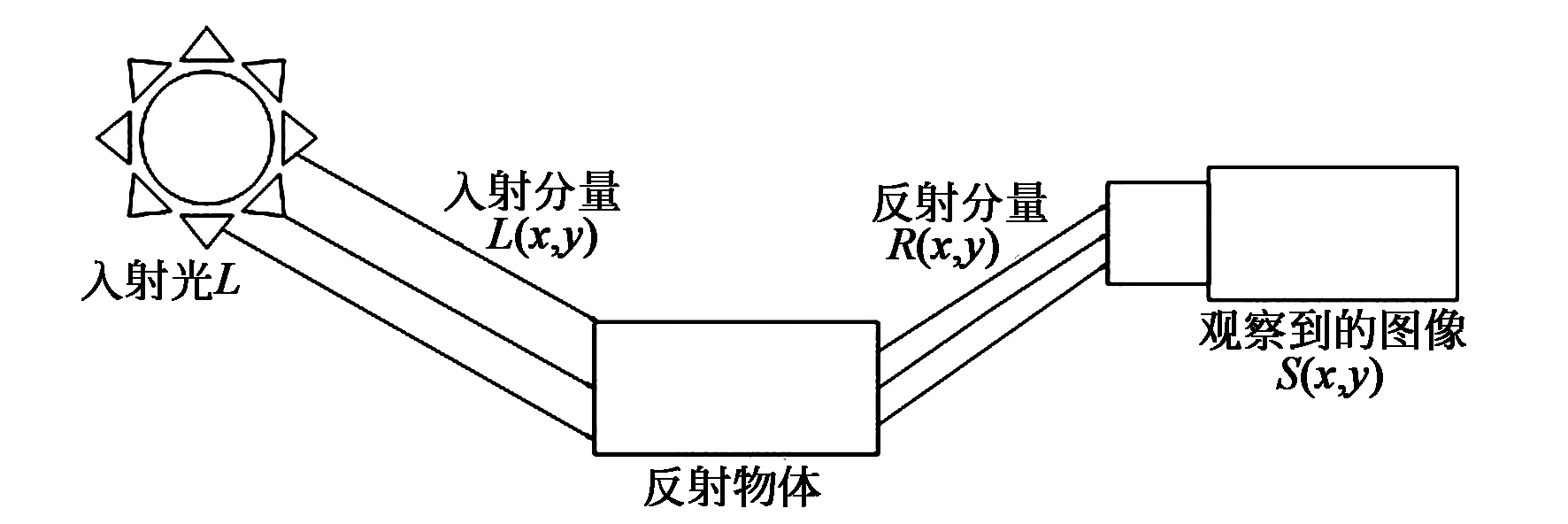
圖1 Retinex模型圖

3 增強算法

本文所提算法，沒有直接估計照度分量或將RGB圖像轉換到其他顏色空間輸入到網絡中訓練。經大量實驗統計發現，在低照度圖像的RGB色彩空間中，照度對R(紅)、G(綠)、B(藍)三個分量都有顯著的影響，因此本文將低照度的RGB圖像以及正常照度的RGB圖像分別分解在R、G、B三個分量上，并構建殘差網絡進行訓練，獲得增強后的三個分量圖像，合成后可得到增強的RGB圖像。本文提出的殘差網絡由1個特征提取模塊、3個雙殘差模塊以及1個重建模塊三部分組成。所提的網絡結構如圖2所示，雙殘差模塊結構如圖3所示。

3.1 特征提取模塊

采用多尺度的濾波器分別對R、G、B三個分量卷積，獲得大量低照度圖像的分量特征信息，進而捕獲特征信息的設計屬性和結構屬性。在這一模塊設置的卷積核的尺寸分別為1×1，3×3，5×5，7×7，每層卷積核的個數均為16。通過不同尺度的卷積提取特征圖，使網絡訓練速度提高。該模塊的計算公式為：

圖2 本文的網絡結構

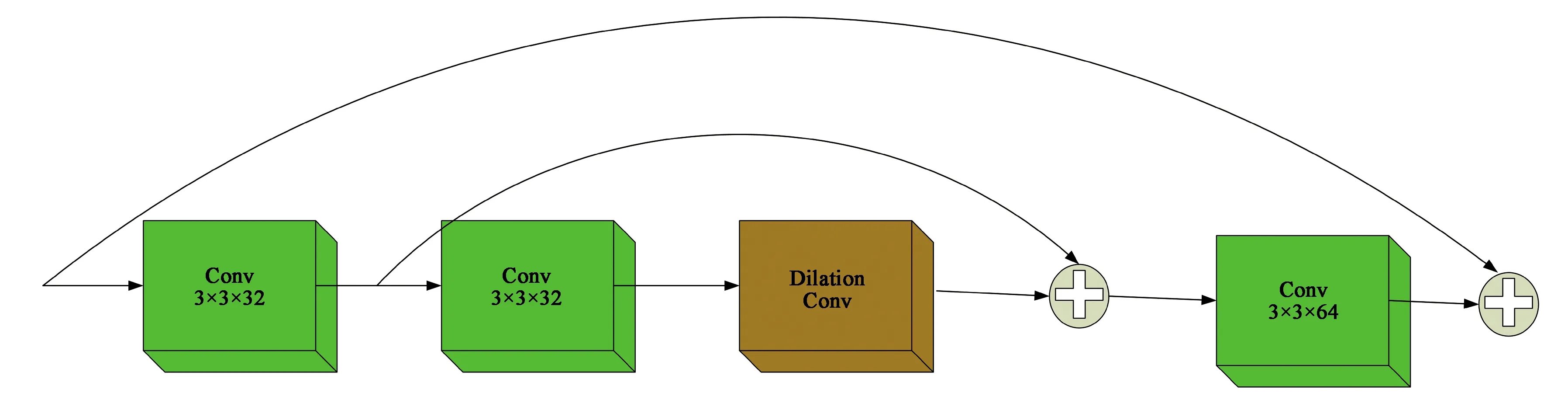
圖3 雙殘差模塊結構

Fi(Y)=Wi*Fi-1(Y)，

(2)

式中：Fi(Y)為輸出的第i層的特征圖，Wi為第i層的卷積核，Fi-1(Y)為第i-1層的特征圖，*表示卷積操作。本文除最后一層，其余每層的末端都使用參數修正線性單元(Prelu)作為激活函數。該激活函數的計算公式為：

PRelu(xi)=max(xi,0)+aimax(0,xi)，

(3)

式中：xi為第i層的正區間輸入信號，ai為第i層的負區間的權系數。除最后一層外，其余各層最終輸出為：

Fsi(Y)=PRelu(Wsi*Y+Bs)，

(4)

式中：Bs為第s層的偏置。

3.2 雙殘差模塊

隨著網絡層數的加深，容易出現梯度彌散、特征信息丟失等問題，本文利用雙殘差模塊來解決此問題。采用3個相同的雙殘差模塊，每個雙殘差模塊由內、外兩個殘差單元和一個3×3×64的卷積層構成。其中，內部殘差單元是由一個3×3×32的卷積層和一個擴張率為2的擴張卷積層組成，外部殘差單元由兩個大小分別為3×3×32和3×3×64的卷積層和內部殘差單元組合而成。通過使用大小為3×3的卷積層以及擴張率為2的擴張卷積。不僅保證了特征圖的輸出表達能力，而且在不改變輸出特征圖的同時，有效提高了網絡的感受野。從而實現網絡的收斂速度加快和梯度的保持。

3.3 重建模塊

通過重建模塊，將圖像的特征信息從特征空間映射到圖像空間，該模塊設計1個卷積層進行圖像重建，使用大小為3×3×1的卷積層，加快網絡的收斂速度，提高網絡的訓練精度。該卷積層用函數表示為：

Fni(Y)=Wni*F(n-1)i(Y)+Bn，

(5)

式中：Fni表示第n層第i組的特征圖，Wni表示第n層第i組的卷積核，Y表示輸入圖像，Bn表示第n層的偏置。

利用均方誤差損失函數(Mean Square Error,MSE)來計算輸入的正常照度圖像與增強后的RGB圖像二者差值的平方和。其計算公式為：

(6)

式中：yi表示第i組正常照度圖像值，xi表示網絡的第i組輸出值，N為樣本的訓練數目。利用自適應矩陣估計法(Adam)和網絡反向傳播算法來最小化MSE的值，從而優化網絡參數。

3.4 利用雙邊濾波優化圖像

為了提高增強后的圖像質量，本文采用雙邊濾波算法進行優化。雙邊濾波算法考慮到像素間的距離因素和灰度值因素，對二者進行非線性組合，自適應地濾波，因此，它對圖像具有較好邊緣保護能力，能夠保留圖像大量的細節特征。雙邊濾波的計算公式為：

(7)

式中：Js表示中心像素s經過雙邊濾波處理的結果，Ip和Is分別表示像素p，s的亮度值，Ω為中心像素的領域，f，g分別為空間域和亮度域的高斯平滑函數。k(s)為歸一化函數，其表達式為：

(8)

4 實驗與結果分析

本節描述了實驗數據、實驗設置及步驟。為了驗證本文算法的效果，對合成和真實的低照度圖像數據集，在主觀和客觀上與經典算法結果對比分析。選取的經典對比算法主要有：Fu算法[6]、Ying算法[7]、Ren算法[8]、Dong算法[14]和Li算法[17]。

4.1 實驗數據及實驗設置

基于Retinex理論模型，本文從數據集Berkeley Segmentation Dataset[19]中選取正常照度圖像，通過光照分量I在(0,1)隨機取值，獲取低照度圖像。將合成的140幅低照度圖像作為訓練數據集，52幅作為測試數據集。圖4展現了正常照度圖像、低照度圖像以及它們分別對應的R、G、B三個分量的圖像。

本文在軟件Matlab R2016a內基于caffe框架進行網絡訓練并測試。在訓練過程中，采用的學習率數值為0.000 1、動量數值為0.9、迭代次數為2.7×105次、卷積核的初始狀態為高斯分布。該網絡訓練采用少量多次的方法，批處理大小為6，使用Adam算法對網絡進行優化。本次實驗的計算機GPU配置為Nvidia GTX 1060。

圖4 正常照度圖像、低照度圖像以及它們分別對應的R、G、B三個分量的圖像。

實驗步驟：

(1)獲取低照度圖像數據集：利用Retinex模型在所用的數據集上獲得低照度圖像；

(2)分解不同類型圖像：將低照度和正常照度RGB圖像同時分解在R、G、B三個分量上；

(3)訓練不同類型圖像的分量：利用殘差網絡模型訓練并測試低照度和正常照度RGB圖像的3個分量；

(4)訓練后合成：將獲得的3個分量圖像合成為RGB圖像，即增強的RGB圖像；

(5)優化圖像：利用雙邊濾波對增強的RGB圖像進行優化，獲得清晰的增強后的圖像；

(6)第一組參照對比：對比網絡訓練后的正常照度的RGB圖像，觀察增強后的RGB圖像效果。

(7)第二組參照對比：對比真實的低照度圖像，觀察增強后的RGB圖像效果；

所提算法流程圖如圖5所示。

圖5 所提算法流程圖

4.2 對合成的低照度圖像實驗結果分析

為驗證本文算法在處理合成的低照度圖像上的優越性，與同等條件下的其他算法對比。從中選取3幅低照度圖像，利用不同算法處理后的效果如圖6～圖8所示。

從主觀上可以看出，Fu算法[6]與Ren算法[8]二者對低照度圖像有一定的增強，但在亮度恢復上遠遠不夠，圖像照度較暗；Ying算法[7]使得增強后的圖像顏色偏白，不符合真實場景；而Dong算法[14]和Li算法[17]在圖像的細節紋理恢復上有明顯的提高，但在亮度上還有一些欠缺。而本文算法的增強效果在亮度上相比于其他算法有很大的提高，而且更完整地表達了局部細節信息。

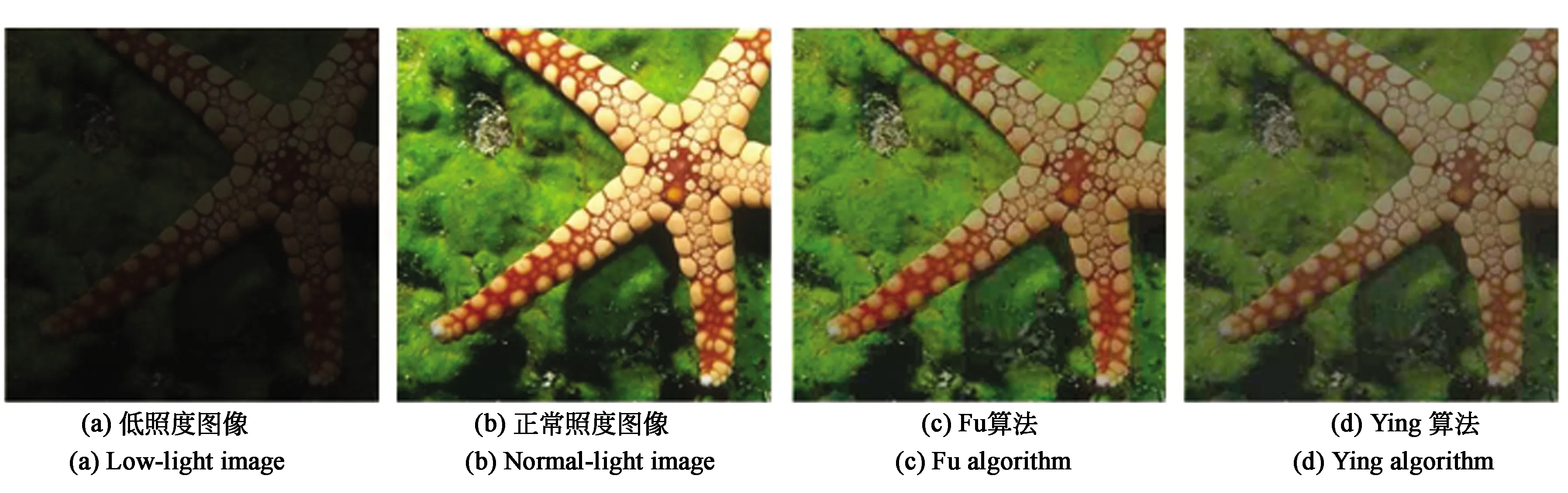
圖6 不同算法處理低照度圖像Starfish的結果

圖7 不同算法處理低照度圖像Bridge的結果

圖8 不同算法處理低照度圖像Building的結果

從客觀上，使用峰值信噪比(Peak Signal to Noise Ratio,PSNR)、結構相似度(Structural Similarity Index,SSIM)、均方根誤差(Root Mean Square Error,RMSE)和信息熵(Information entropy)重要的圖像評價指標來衡量增強獲得最終正常照度圖像的質量。

各個評價指標的計算公式為：

(9)

式中：x為正常照度的圖像，y為增強后的圖像。峰值信噪比可以用來評價圖像質量，其值越高，表明處理后圖像增強效果越好，反之效果越差。

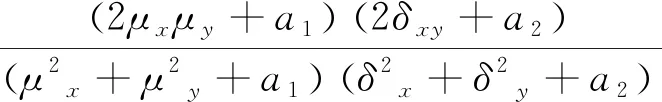
(10)

式中：x，y分別為增強的圖像和參考的正常照度的清晰圖像，μx為x的平均值，μy為y的平均值，δ2x為x的方差，δ2y為y的方差，δxy為x和y的協方差。a1和a2是比較小的常數，以避免分母為0而出現的系統不穩定現象，SSIM的取值在[0,1]。SSIM的值越大，意味著圖像失真越小，增強效果越好。

(11)

式中：Y為正常照度圖像，X為增強后的圖像，n為圖像像素總數。均方根誤差表示增強后的圖像與參考的正常照度圖像之間的差異，RMSE的值越小，表示增強的效果越好。

H(X)=E[log2P(X)-1]，

(12)

式中：X表示隨機變量，P(X)表示輸出概率函數。信息熵是指圖像包含信息量多少程度的物理量。其值越大，包含的信就越多，表明增強效果越好。如表1～表3所示。

表1 圖像Starfish采用不同算法增強后評價指標結果

表2 圖像Bridge采用不同算法增強后評價指標結果

表3 圖像Building采用不同算法增強后評價指標結果

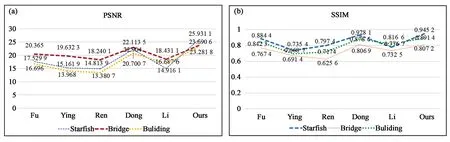
圖9 峰值信噪比(a)和結構相似度(b)的對比結果

從客觀方面可以看出，根據表1～表3，以及圖9，本文所提算法在峰值信噪比(PSNR)、結構相似度(SSIM)、均方根誤差(RMSE)和信息熵(Information entropy)這些評價指標都要優于其他對比算法，說明本文的算法對于增強低照度圖像有很大的提升。

為證明本文所提的雙殘差模塊在增強低照度圖像上的效果，運用控制變量法，在網絡深度不變的前提下，將網絡中的雙殘差模塊分別替換為僅含有卷積層模塊和常規的殘差模塊，對模型進行分析。采用常用的峰值信噪比(PSNR)和結構相似度(SSIM)對3種模型進行定量測評。表4為實驗結果對比值。

由表4可知，本文所提的雙殘差網絡模型，其峰值信噪比(PSNR)和結構相似度(SSIM)最高可達25.931 1 dB和0.945 2，都優于其他兩種網絡模型。

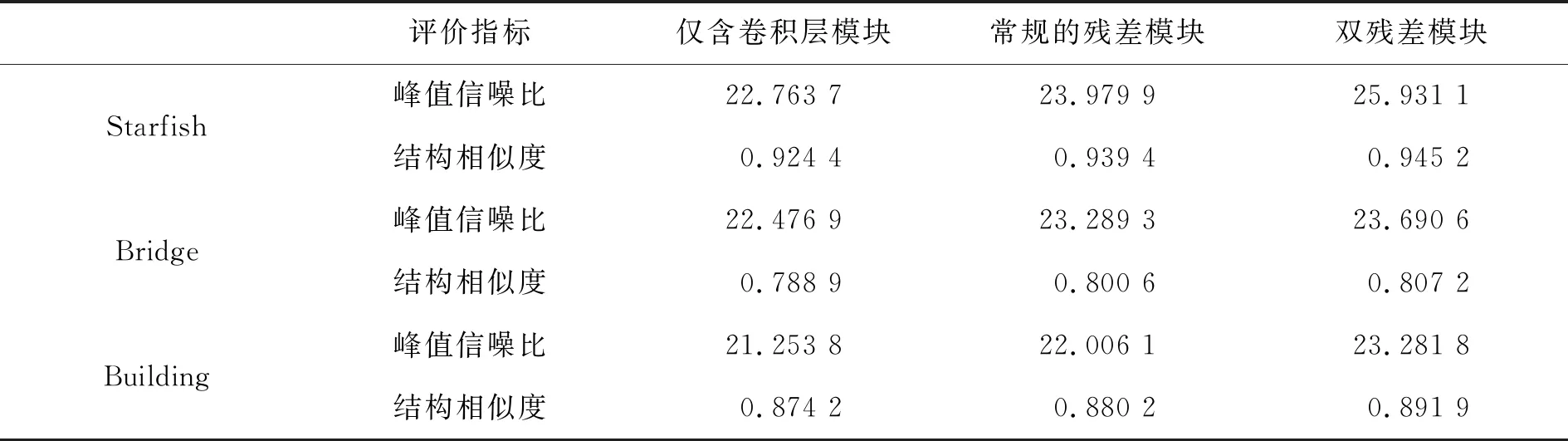
表4 不同模塊的PSNR(單位：分貝)和SSIM的對比結果

4.3 對真實的低照度圖像實驗結果分析

本文算法在處理合成的低照度圖像上具有明顯的增強效果。為了進一步證明本文算法的優越性，基于真實的低照度圖像，本文算法與其他5種算法進行對比如圖10～圖11所示。 圖10和圖11分別是Fu算法[6]和MEF[20]數據集中的真實的低照度圖像。

為驗證本文算法處理真實低照度圖像的效果，采用盲圖像質量評估方法(NBIQA)、圖像均值(Image average)、平均梯度(Average Gradient)和標準差(Standard Deviation)4個重要的無參考圖像的評價指標以及算法運行時間，對增強后的圖像進行定性對比。盲圖像質量評估的值通常在0和100之間，其值越小，表示圖像質量越好。圖像均值表示圖像亮度大小的物理量，其值越小，其亮度越低。平均梯度表示圖像紋理細節的變化特征，其值越大，圖像越清晰。標準差表示灰度均值的離散程度，其值越大，圖像質量越好。4個評價指標值對比結果如表5～表6所示，運行時間對比結果如表7所示。

圖10 不同算法處理真實的低照度圖像Pocky的結果

圖11 不同算法處理真實低照度圖像Palace的結果

一些評價指標的計算公式為：

圖像均值：

(13)

式中：N為像素總個數。

平均梯度：

(14)

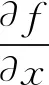
標準差：

(15)

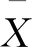
表5 圖像Pocky采用不同算法增強后評價指標結果

表6 圖像Palace采用不同算法增強后評價指標結果

表7 不同算法的運行時間對比結果(單位：s)

對于圖10～圖11，從主觀方面，Fu算法[6]、Ying算法[7]以及Ren算法[8]對于增強后的圖像在亮度恢復上還不夠，增強后的圖像在色彩上不夠自然；而Dong 算法[14]雖然對于亮度有明顯效果，但對于Pocky圖像的部分紋理細節增強過度；Li算法[17]增強后的圖像出現了偽影，視覺上不清晰。本文算法增強后的圖像在亮度和色彩恢復上更加自然，視覺效果更佳。從客觀方面，在表5～表6中，對不同的評價指標，總體上本文算法要優于其他對比算法，增強低照度圖像效果顯著。根據表7可知，本文算法的運行時間最短，效率最高，應用更方便。

5 結 論

本文提出的基于雙殘差卷積網絡的低照度圖像增強算法，改進了傳統算法直接處理照度分量或直接分解到其他顏色空間。所提算法構造雙殘差網絡，分別對R、G、B三個分量進行訓練，有效地提高了網絡模型的預測精度。其次，本文采用的殘差模塊改進了常用的殘差單元，通過使用卷積層和擴張卷積層構成的內外雙殘差網絡模塊，增大圖像的感受野，加速網絡的收斂。最終，再對增強后的RGB圖像使用雙邊濾波進行優化，保留了圖像更多的邊緣信息。實驗結果表明，與其他對比算法相比，所提算法不僅有較好的增強效果，也加快了運行速度，能更好地應用于實際。