電廠脫硫系統閉環子空間辨識方法研究

楊大州，張尋，姜昊，劉暢，李益國

(1.大唐環境產業集團股份有限公司特許經營分公司，南京 211106；2.東南大學能源與環境學院，南京 210096)

近年來，大氣污染問題日益嚴峻，電站煤燃燒排放的大量SO2則是大氣污染的主要污染之一[1]。煙氣脫硫技術是世界上唯一大規模商業化應用的脫硫方法，其中，石灰石-石膏濕法煙氣脫硫技術是應用最廣泛和最成熟的脫硫工藝技術。但是，脫硫系統是一個典型的大慣性和非線性的多變量控制系統，傳統的PID控制難以滿足脫硫系統的控制要求。

為了研究電廠脫硫系統控制策略，建立高精度數學模型是首要工作。目前最常見的系統建模方法主要有機理建模方法與數據辨識建模方法。機理建模需要熟知控制系統的內在機理，且計算復雜，而電廠脫硫系統的被控對象往往具有非線性以及大慣性的特點，且脫硫工藝流程繁多，系統特性復雜，不適合應用機理建模方法；其次，當脫硫系統自動控制投入時獲得的運行數據，其輸入變量和輸出變量之間存在相關性，采用最小二乘法等一般的開環辨識方法難以實現對模型參數的無偏估計；再者，從自適應控制的角度看，為了應對脫硫系統的慢時變特性，也需要研究系統的閉環辨識方法。

子空間辨識方法可以直接獲得被控對象的狀態空間模型，便于進行多變量預測控制器的設計。本文采用兩種多變量閉環子空間辨識方法，建立脫硫系統的兩輸入兩輸出的狀態空間模型，并與開環子空間辨識方法進行仿真比較與動態特性分析。

1 濕法石灰石脫硫系統

濕法石灰石煙氣脫硫技術是目前世界上最廣泛使用和最成熟的脫硫工藝技術，采用石灰石作為脫硫吸收劑，除去煙氣中的SO2[2]。該技術脫硫效率較高，運行較為可靠穩定，并且能夠適應大容量機組和高濃度SO2煙氣條件。但是，濕法石灰石脫硫系統的控制問題是其發展的最大阻礙之一。

典型的濕法石灰石煙氣脫硫系統可劃分為煙氣系統、吸收塔系統、石灰石漿液制備系統與石膏脫水系統，其中最核心的子系統是吸收塔系統，吸收塔內脫硫過程示意圖如圖1所示。幾乎整個脫硫反應都是在吸收塔內完成的。

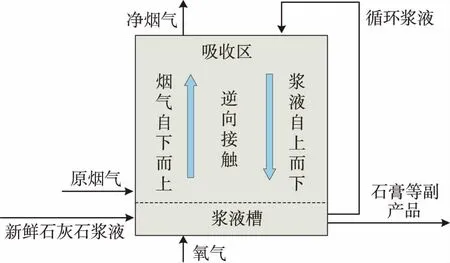
圖1 吸收塔內脫硫過程示意圖

原煙氣降溫后從吸收塔底部進入。新鮮石灰石漿液從漿液槽送入，與反應后下落至漿液槽的石灰石漿液相互混合。混合后的漿液通過循環泵實現循環使用，而經過結晶沉淀后的石膏等副產品被不斷吹掃防止聚集，并被運送到儲蓄罐中。吸收區內，循環漿液從吸收塔頂部由噴嘴噴出，自上而下的漿液與自下上升的煙氣逆向接觸，發生一系列化學反應，除去煙氣中的SO2。凈化后的煙氣經升溫后從煙囪排出。

2 閉環子空間辨識方法

閉環子空間辨識方法越來越受到關注，相較于開環辨識方法，其用于脫硫系統辨識有以下幾點優勢：

1)由于工業生產過程常常具有很大的干擾，開環辨識會使得系統在大范圍內變得非線性；

2)閉環辨識有利于控制系統的設計，閉環辨識所得到的模型在控制算法設計相關的頻率范圍內是相當準確的，而且對于一些特殊的控制系統設計方法，閉環辨識的方差也要小于開環辨識；

3)閉環子空間辨識大多數都有在未來輸入的補空間進行正交投影計算的步驟，從而可將噪聲項消除[3]。

目前國內外閉環子空間辨識方法應用較多的方法主要有基于正交投影的閉環子空間辨識方法(Closed-loop Subspace Orthogonal Projection Identification Method，CSOPIM)[4]與基于新息估計的閉環子空間辨識方法(Parallel parsimonious SIM with Estimation，PARSIME)[5]。

2.1 子空間辨識的基礎知識

考慮如下的離散線性時不變狀態空間模型：

(1)

式(1)中，xk∈n為系統的狀態變量；uk∈nu為輸入觀測向量；yk∈ny為輸出觀測向量；wk∈n與vk∈ny分別為系統的測量噪聲與過程噪聲。

假設系統是能觀測的，可設計如下Kalman濾波器：

(2)

式(2)中，K為卡爾曼濾波增益。

(3)

式(3)中，新息ek為零均值白噪聲。

定義輸入數據Hankel矩陣Up與Uf：

定義狀態序列Xi=[xixi+1…xi+j-2xi+j-1]∈n×j，則過去狀態序列為Xp=X0=[x0x1…xj-2xj-1]，未來狀態序列為Xf=Xi=[xixi+1…xi+j-2xi+j-1]。

首先考慮以下狀態預測方程：

x1=Ax0+Bu0+Ke0

x2=Ax1+Bu1+Ke1

(4)

=A(Ax0+Bu0+Ke0)+Bu1+Ke1

類推可得到i時刻系統狀態變量與i，i+1，…，i+j-1時刻的狀態預測，并代入新息形式的狀態空間模型式(3)，可得到系統i時刻與0，1，…，i-1時刻的輸出。

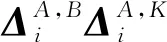
Γi=[CCA…CAi-1]T

由此得到構造的Hankel矩陣Yp，Yf以及Ep，Ef，下標p和f分別表示過去和將來相對時間的概念：

Yp=ΓiXp+HiUp+GiEp

(5)

(6)

Yf=ΓiXf+HiUf+GiEf

(7)

2.2 基于正交投影的閉環子空間辨識方法

CSOPIM辨識方法是基于正交投影的辨識方法，從控制對象的輸入輸出著手辨識對象模型，通過正交投影將輸入輸出數據轉化為卡爾曼狀態序列，再求出系統矩陣[6]。關鍵是引入了包含設定值Hankel矩陣的輔助變量。

2.2.1 基于正交投影的子空間辨識方法

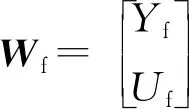
(8)

對Z進行SVD分解如下：

(9)

理論上Z的秩應該為nui+n，所以根據上述SVD分解結果進行階次判定。

根據式(9)可知Z的正交補空間為U2。取M為單位矩陣，矩陣U2M可分解為U2M=(P1P2)T，簡單變形得到：

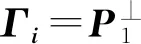
(10)

但是上述方法用于系統閉環辨識效果并不理想，一種可行的解決方法是引入包含設定值Hankel矩陣的輔助變量[8]：

(11)

需要指出的是，輔助變量的構造方法并不是唯一的。

2.2.2 系統矩陣的計算方法

卡爾曼濾波狀態可根據式(12)計算得到：

(12)

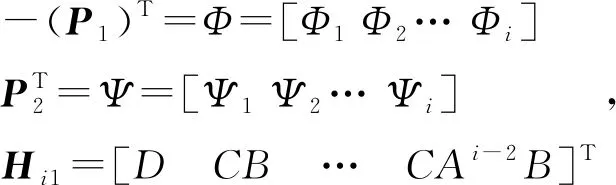
(13)

根據式(13)可求出Hi1，并構造出Hi。

定義：Rf=Ri+1|2i-1Up=U0|iYp=Y0|i

Uf=Ui+1|2i-1Yf=Yi+1|2i-1，從而得到：

(14)

式(14)中，Γi為Γi去掉最后ny行得到，Hi由Hi去掉最后ny行與nu列得到。

系統的參數矩陣A，B，C，K可根據以下公式求解得到：

(15)

但是該方法在閉環系統中應用效果可能不理想，由于反饋控制律的存在，Ui|i可能與Xi相關，從而導致有偏估計問題。為了解決這一問題，可以通過下述步驟求解：

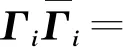
2)假定系統的參數矩陣中D=0；

3)參數矩陣B與K可以通過下式求解：

(16)

2.3 基于新息估計的閉環子空間辨識方法

在閉環辨識環境下，未來輸入與過去噪聲是相關的，使得正交投影不能消除噪聲項，所以基于正交投影的子空間辨識在閉環下會存在有偏估計。而基于新息估計的閉環子空間辨識方法(PARSIME)的基本思想為由上一行的估計新息序列結果帶到下一行中，下一行估計得到的值繼續應用到后面的一行，即PARSIME算法從第一行塊中估計新息序列，然后認為是已知新息去估計其它模型參數。

2.3.1 基于新息估計的子空間辨識方法

閉環子空間辨識與開環子空間辨識最大的不同在于未來輸入數據與過去噪聲數據存在相關性，故需要先將相關性消除，然后再進行無偏差辨識。在PARSIME方法中考慮將Hankel矩陣Yf按行分塊：

Yf=[Yf1Yf2…Yfi…Yff]T，i=1，…，f

(17)

采用2.1節中類似的方法，得到如下的矩陣等式：

(18)

式(18)中，

Γfi=CAi-1

Hfi=[CAi-2B…CBD]?[Hi-1…H1H0]

Gfi=[CAi-2K…CKI]?[Gi-1…G1G0]

(19)

每一行需要計算Efi的估計值，計算如下：

(20)

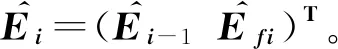
當i=1時有：

(21)

(22)

因為新息序列已經得到估計值替代原始數據，故未來輸入數據不再與新息序列相關，直接使用最小二乘求解。

借鑒其它子空間辨識方法，可確定權矩陣如下[9]：

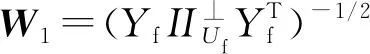
(23)

(24)

2.3.2 系統矩陣的計算

關于系統矩陣的計算，根據上述計算結果重構系統狀態，再進行系統矩陣的計算[10]。其具體計算步驟如下：

4)計算系統參數矩陣A，B與K，用MATLAB矩陣形式表示如下：

(25)

PARSIME方法將整體辨識模型分解為若干子模型，通過對子模型進行多步計算，避免了回歸框架中對冗余非因果參數的重復估計，同時對新息模型計算得到新息估計值來代替系統噪聲估計值，消除噪聲的影響，解決了基于正交投影的閉環子空間辨識方法的有偏估計問題。

3 脫硫系統的閉環子空間辨識

3.1 閉環數據生成

針對某脫硫系統的傳遞函數模型[11]式(26)，采用基于擴增狀態空間模型的預測控制器對該模型進行控制，生成閉環數據的預測控制器參數見表1。

(26)

式(26)中，pH表示漿液的pH值；SO2表示出口的SO2濃度，10-6；Q表示石灰石供給泵轉速，r/min；L表示漿液循環泵電機頻率，Hz。

以脫硫系統某運行平衡點為基準，令pH和SO2設定值按方波形式變化，同時在輸入和輸出變量上疊加白噪聲信號，以模擬測量噪聲，閉環數據生成相關參數見表2。仿真時間為15 000 s，最終生成的閉環輸入和輸出數據如圖2與圖3所示。

表1 生成閉環數據的預測控制器參數

圖2 生成的閉環輸入數據

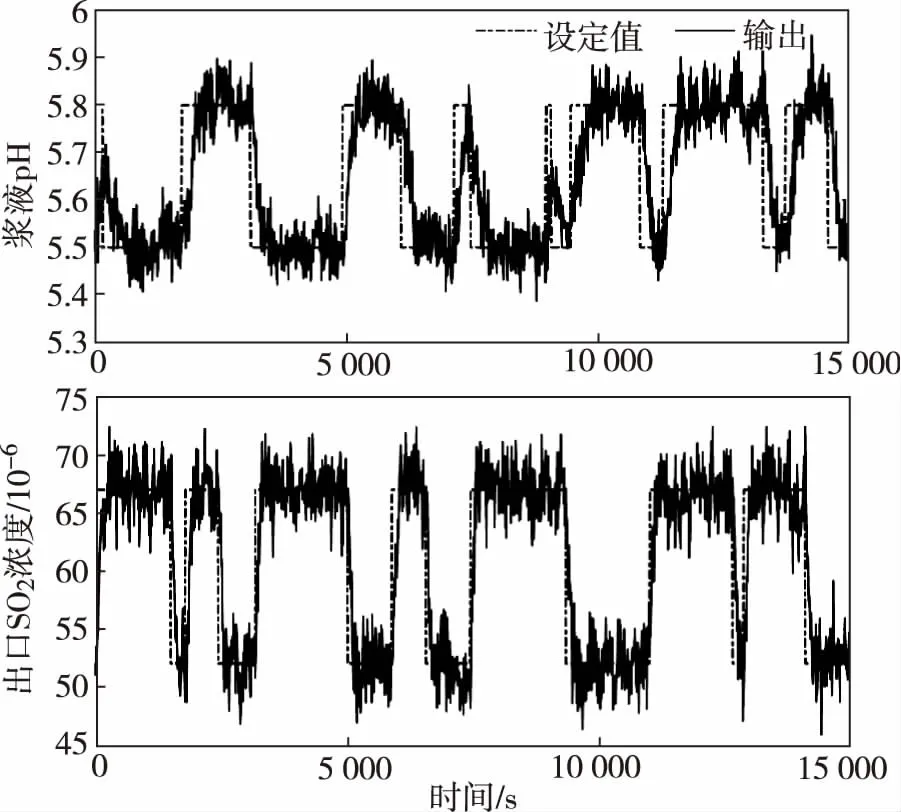
圖3 生成的閉環輸出數據

3.2 閉環子空間辨識

3.2.1 辨識結果

分別采用CSOPIM與PARSIME辨識方法，計算得到的狀態空間模型的系統矩陣如下：

CSOPIM方法的辨識結果：

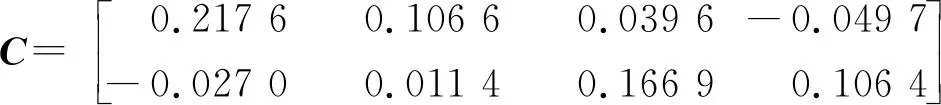
PARSIME方法的辨識結果：

3.2.2 數據擬合效果對比分析

將兩種閉環子空間辨識方法CSOPIM和PARSIME以及開環子空間辨識方法N4SID，與原始閉環數據的擬合效果進行對比，基于閉環數據的三種辨識方法辨識效果比較如圖4所示。將每種辨識方法得到的兩個輸出量分別與原始閉環數據作差，得到輸出量的誤差，再計算輸出量的絕對誤差平均值與誤差標準差，基于閉環數據的三種辨識方法的辨識效果比較指標見表3。由圖表可知，閉環子空間辨識方法的效果總體比開環子空間辨識方法好，PARSIME方法的辨識效果優于CSOPIM方法。

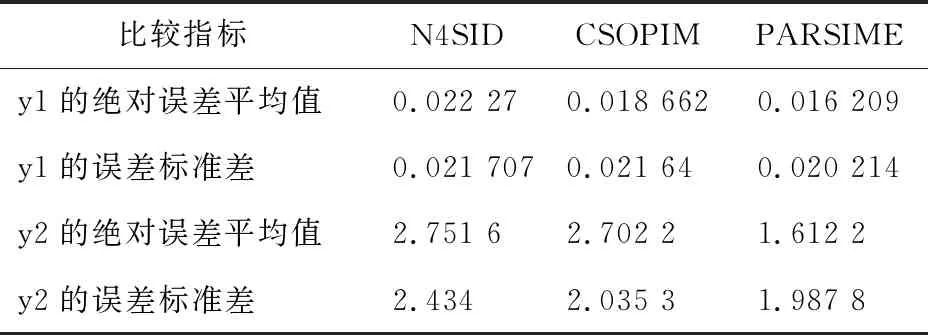
表3 基于閉環數據的三種辨識方法的辨識效果比較指標

從理論角度來說，N4SID方法適用于開環數據的辨識，且易受干擾影響，因此N4SID方法用于閉環辨識效果不好。CSOPIM方法雖然屬于閉環辨識方法，但是由于正交投影無法消除噪聲項的影響，存在有偏估計的問題，而PARSIME方法通過將未知新息序列視為已知參數，從而能夠得到系統參數的一致估計值，通過估計值來代替系統噪聲估計值，以消除噪聲的影響。因此PARSIME方法的辨識效果會更好。

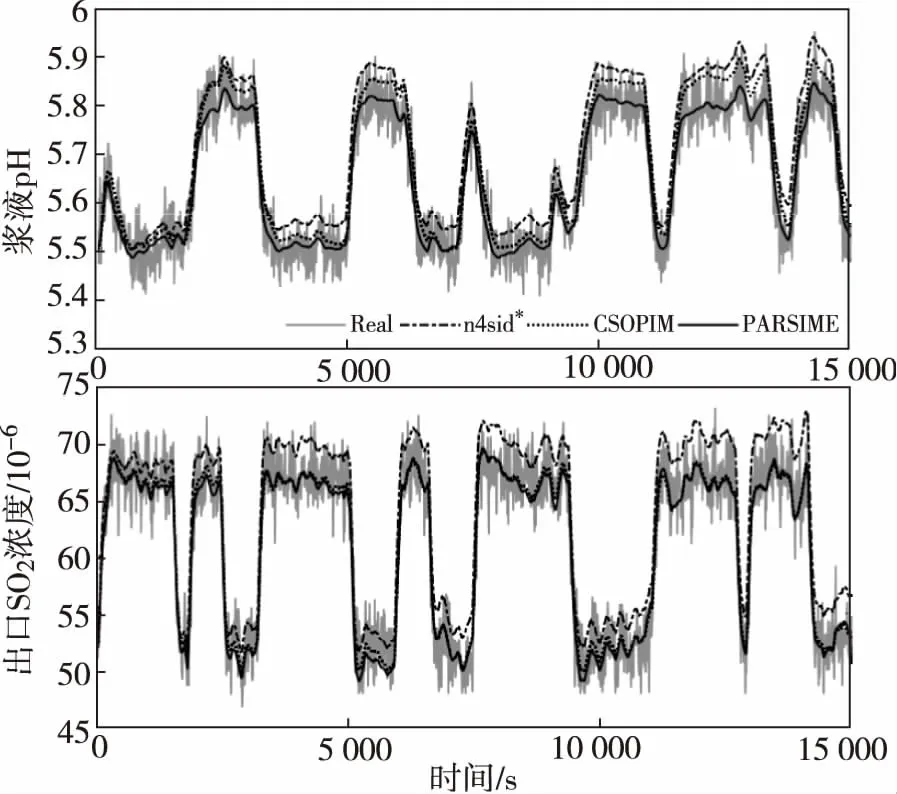
圖4 基于閉環數據的三種辨識方法辨識效果比較

3.2.3 階躍響應對比分析

以表2中平衡點為基準，對石灰石供給泵轉速做+1 r/min的階躍，保持漿液循環泵頻率不變，石灰石供給泵階躍響應曲線比較圖如圖5所示；另外對漿液循環泵頻率做+1Hz的階躍，保持石灰石供給泵轉速不變，漿液循環泵階躍響應曲線比較如圖6所示。

綜合分析圖4、圖5和圖6可知，不管是從數據擬合效果，還是從階躍響應曲線，對于閉環數據而言，閉環子空間辨識方法的效果都比開環子空間辨識方法好，同時PARSIME方法的辨識效果優于CSOPIM方法。

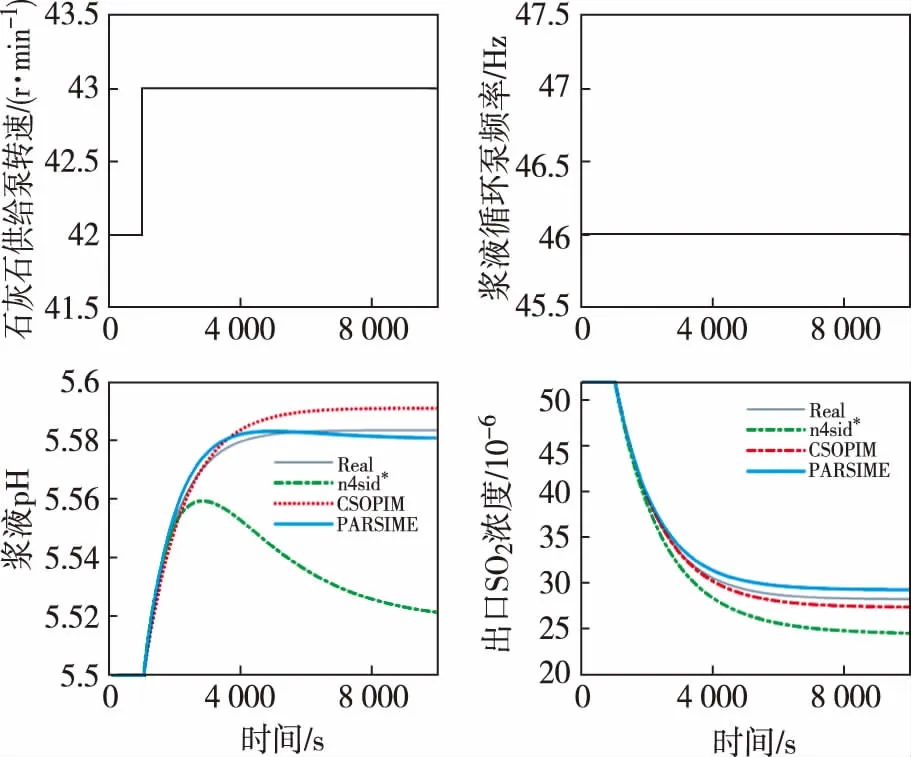
圖5 石灰石供給泵階躍響應曲線比較

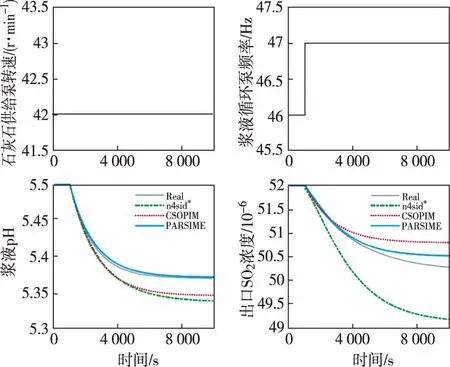
圖6 漿液循環泵階躍響應曲線比較

3.3 模型動態特性分析

分析圖5可知，當石灰石供漿量增大時，由于新增的石灰石的溶解，漿液pH開始增大，同時吸收塔出口SO2濃度開始降低。當石灰石溶解速率與SO2吸收速率相等時，系統達到新的穩定狀態。兩者的變化方向相反，都屬于大慣性和有自平衡能力的被控對象，其上升時間達3 000 s左右。

分析圖6可知，當漿液循環流量發生階躍變化時，由于液氣比增加，煙氣中更多的SO2被捕獲，因此漿液pH和出口SO2濃度同時減小。pH的減小由離子液體相的緩沖能力阻止，并且隨著漿液中石灰石的逐漸溶解pH降低幅度慢慢減小。因為SO2的吸收速率大于石灰石溶解速率，所以離子液體相的緩沖能力耗盡，pH繼續減小。SO2吸收速率隨之降低，石灰石溶解速率提高。當兩者速率相等時，系統達到新的平衡。兩者都屬于大慣性和有自平衡能力的被控對象，但漿液循環流量變化對pH的影響明顯快于對SO2濃度的影響。

通過分析，對濕法脫硫系統的主要動態特性總結如下：

1)由于脫硫系統的石灰石溶解速率低，出口SO2濃度和漿液pH的動態特性較慢。因此，需要在控制器設計中考慮輸出預測和動態超調等措施，以改善系統的調節品質。

2)漿液循環流量變化對出口SO2濃度的影響在初期比較明顯，但是在低Ca/S(pH)比運行時，漿液循環流量變化對出口SO2濃度幾乎沒有影響。這就表明，脫硫系統SO2吸收能力主要取決于外部石灰石的供給。

4 結語

本文采用基于正交分解和基于新息估計兩種典型的閉環子空間辨識方法，建立了脫硫系統的狀態空間模型，并對其有效性進行了對比分析。通過將兩種閉環子空間辨識方法的辨識效果與開環子空間辨識方法N4SID進行對比，驗證了閉環子空間辨識方法的有效性。同時通過理論分析與辨識效果比較，發現以PARSIME方法建立的脫硫系統的動態數學模型精度優于CSOPIM方法。此外，本文對濕法脫硫系統主要動態特性做出總結，為脫硫系統先進控制策略的研究奠定基礎。