基于BP人工神經網絡噴射成形7055鋁合金的本構模型

羅 銳, 曹 赟, 邱 宇, 崔樹剛, 周皓天, 周易名,袁 飛, 張肖佩佩, 程曉農*

（1.江蘇大學 材料科學與工程學院，江蘇 鎮江 212013；2.中國航空制造技術研究院，北京 100024）

7055鋁合金屬于超硬Al-Zn-Mg-Cu系變形鋁合金[1]，該合金具有優異的綜合力學性能，目前已被廣泛應用于航空航天領域飛行器部件的制造當中，例如空客A380大飛機的壓力艙桁條與上機翼桁條均采用7055鋁合金[2-4]。但是在整個零部件制造流程中，傳統鑄造工藝帶來的成分偏析容易使合金發生熱裂失效，很難滿足高標準航空航天部件的服役要求[5-6]。而噴射成形是一種“近終形”成形技術，利用合金霧化快速沉積凝固的方式，大幅提高合金元素的固溶程度且晶粒組織均勻細小，有助于后續熱加工環節的進行[7]。在熱加工制造環節中，噴射成形7055鋁合金還需要進行熱擠壓、鍛造等多道熱加工工序，不當的熱加工工藝易引發合金的開裂失效。高溫流變應力曲線能夠綜合反映各熱加工工藝參數與合金組織演變之間的內在聯系，因此研究該材料的高溫變形行為具有重要的工程意義。

揭示合金在熱加工過程中的變形規律及其本構關系是研究其高溫變形行為的基礎。科研人員通常采用傳統唯象型Arrhenius本構模型建立材料的本構關系，然而合金的變形過程受到多方面因素的共同影響，致使流變應力與各加工參數之間呈現出復雜的非線性關系，基于回歸算法的傳統Arrhenius型本構方程常難以保證流變應力值的精準預測[8]。例如Wu等[9]和Wang等[10]分別利用傳統唯象型Arrhenius本構模型研究2024A鋁合金與2219鋁合金的流變應力情況，預測值的平均相對誤差值高達5.02%和3.11%。隨著計算機技術的不斷發展，近年來迅速成熟的基于BP人工神經網絡的本構模型依靠其自組織、自修正以及內插、外插的技術特點能夠有效得耦合多元變量、解決非線性問題并大幅提高模型準確度[11]。Wang等[12]利用該模型預測Al-Zn-Mg-Sc-Zr合金的流變應力情況，其相關系數高達0.9984，而Arrhenius本構模型的相關系數僅為0.9887。對于航空航天用噴射成形7055鋁合金來說，構建材料的本構模型并精確預測其加工過程中的流變應力演變規律迫在眉睫。

通過先進的Gleeble熱力模擬技術對噴射成形7055鋁合金（擠壓態）進行等溫熱壓縮實驗，獲取該合金的高溫流變應力曲線，并依據曲線數據分別構建該合金的傳統唯象型Arrhenius本構方程以及BP神經網絡型本構方程。通過流變應力預測值的對比，分析該兩種模型的精準程度，并為工業生產中熱加工參數的制定提供理論指導。

1 實驗及方法

本實驗所涉及的噴射成形7055鋁合金（擠壓態），其化學成分如表1所示。將合金加工成φ10 mm × 15 mm的圓棒狀試樣，并利用Gleeble-3500型熱力模擬試驗機對其進行等溫熱壓縮實驗。壓縮前，在試樣兩端粘貼石墨片以起到潤滑以及防止鼓肚效應的作用。將試樣加熱至變形溫度（350 ℃、375 ℃、400 ℃、425 ℃、450 ℃），保溫30 s后進行不同應變速率下（1 s-1、5 s-1、10 s-1、20 s-1）的熱壓縮，其熱變形工藝如圖1所示。壓縮完成后立即淬火冷卻至室溫。將實驗獲取的熱壓縮數據進行圖像化處理，獲得流變應力曲線并進行后續研究。

表 1 實驗用噴射成形7055鋁合金的化學成分（質量分數/%）Table 1 Chemical composition of experimental 7055 aluminum alloy（mass fraction/%）

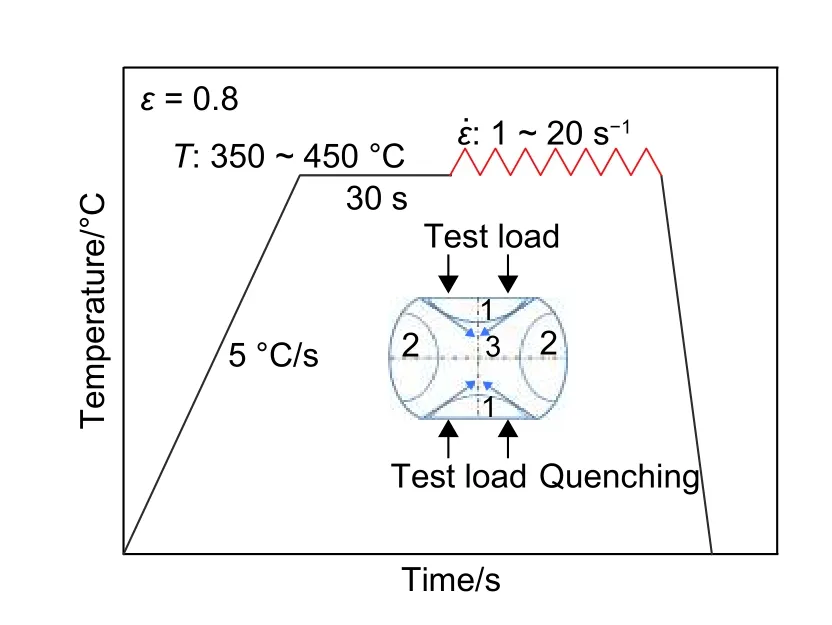
圖 1 熱變形工藝流程Fig. 1 Hot deformation process flow diagram

2 結果與討論

2.1 材料應力-應變曲線

如圖2所示，根據實驗所得熱壓縮數據，獲得7055鋁合金的流變應力曲線。由圖2可得，形變初期，流變應力值隨應變量的增加而急劇上升。這是由于形變初期，合金內部的位錯迅速糾纏、增殖，位錯密度大幅上升造成材料發生加工硬化現象[13]。隨著應變量的進一步增加，可動位錯數量上升，且由于該合金較高的層錯能，擴展位錯易發生束集、交滑移，有效起到動態軟化的作用[14]。當加工硬化與動態軟化達到平衡狀態時，流變應力曲線呈現出穩態平臺且具有動態回復特征。綜合對比圖2（a）、（b）與圖2（c）、（d）可知該合金的流變應力對于變形溫度（T）與應變速率（ε˙）較為敏感。其流變應力值與變形溫度（T）呈現出負相關，而與應變速率（ε˙）呈現出正相關。

2.2 唯象型Arrhenius本構方程

唯象型Arrhenius 本構方程是當下廣泛運用的流變應力預測模型。該模型是由Sellars等[15-16]學者提出的。

本文利用該模型對應變量為0.15的7055鋁合金進行Arrhenius本構方程研究，其相應的擬合過程如圖3（a）～（d）所示。通過斜率以及截距的運算處理，得到各材料常數分別為n1= 7.7406；β=0.0791；α=β/n1= 0.0102；n= 6.1473。同時，熱變形激活能Q的計算值為76.6704 kJ?mol-1，處于較低水平，顯示該合金具有較好的熱加工成形性能。

Zener-Hollomon指數（Z）與合金的動態軟化程度具有一定相關性[17]。其公式如式（1）所示。對該公式進行對數運算得到式（2）。

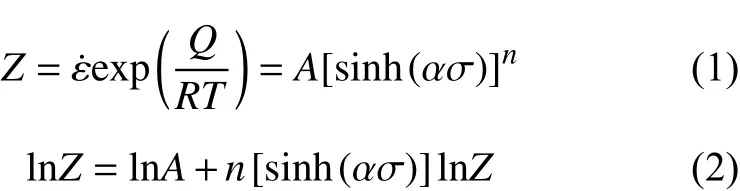
故該噴射成形7055鋁合金在應變量為0.15時的Arrhenius型本構方程可表示為：

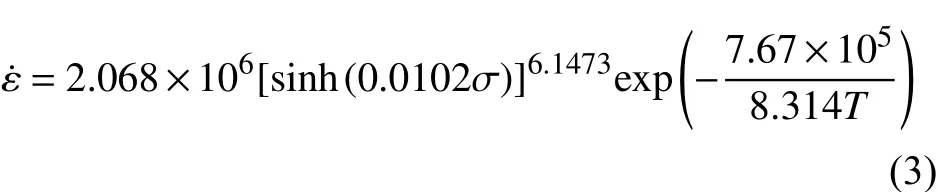
然而合金的流變應力與各變形參數間并非簡單的線性回歸關系，上述本構方程算法缺乏對應變量等其他因素影響的考量。故下文將在上述研究的基礎上耦合應變量因素，以使得本構方程能夠更加精準地預測合金的流變應力狀態。

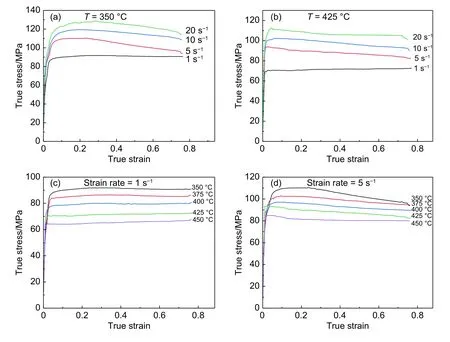
圖 2 噴射成形7055鋁合金不同參數下的流變應力曲線Fig. 2 Flow stress curves of spray forming 7055 aluminum alloy with various deformation parameters（a）350 ℃；（b）425 ℃；（c）1 s-1；（d）5 s-1

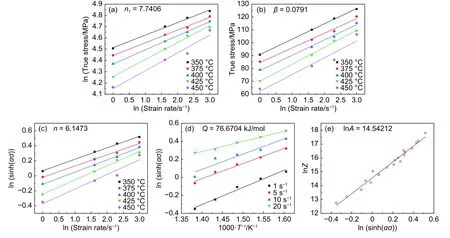
圖 3 噴射成形7055鋁合金不同本構參數關系曲線（應變量0.15）Fig. 3 Relationship curve of various constitutive parameters of spray forming 7055 aluminum alloy（strain 0.15）（a）lnε˙-lnσ ；（b）lnε˙-σ ；（c）lnε˙-l n(sinh(ασ))； （d）-l n(sinh(ασ))； （e）l n(sinh(ασ))-lnZ

基于耦合精度以及計算負荷的綜合考慮，本研究中將從應變量0.05～0.7的流變數據中每間隔0.025的應變量取一參數點，并對各應變量參數下的材料參數值進行6次多項式擬合，擬合圖像如圖4所示。從圖4中可得，各參數的擬合相關度較為良好。α以及n值在應變量為0.2左右處出現一極小值，而Q與lnA值則在應變量0.3之后幾乎保持一水平線。表明該合金在0.3以下的較小變形量下，其塑性加工性能變化浮動較大，而0.3以上的較大變形量狀態下塑性加工性較為穩定。各材料常數與應變量的數據關系詳見表2。

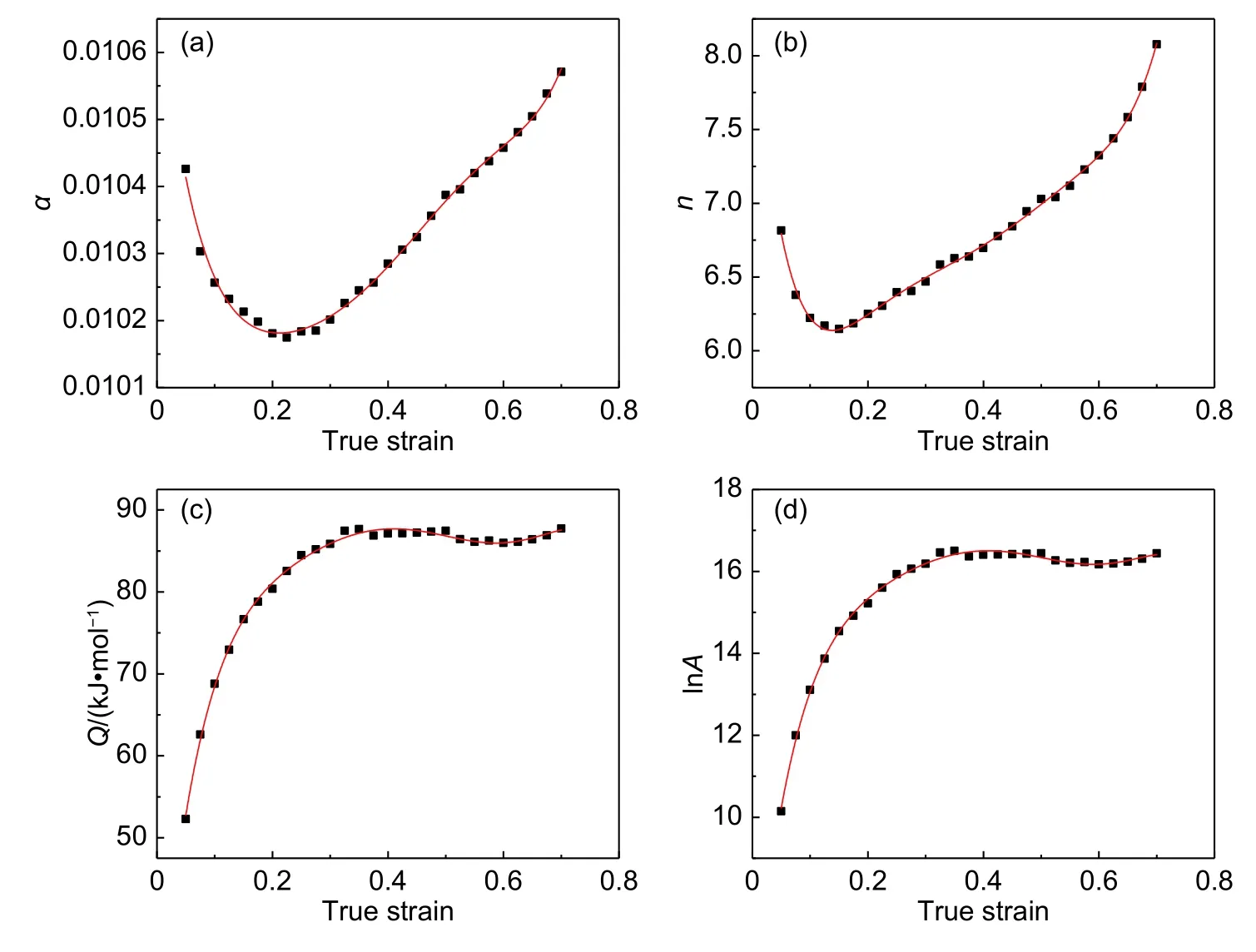
圖 4 不同本構常數與應變量之間的關系Fig. 4 Relationship between various constitutive constant and ture strain （a）α-ε；（b）n-ε；（c）Q-ε；（d）lnA-ε；

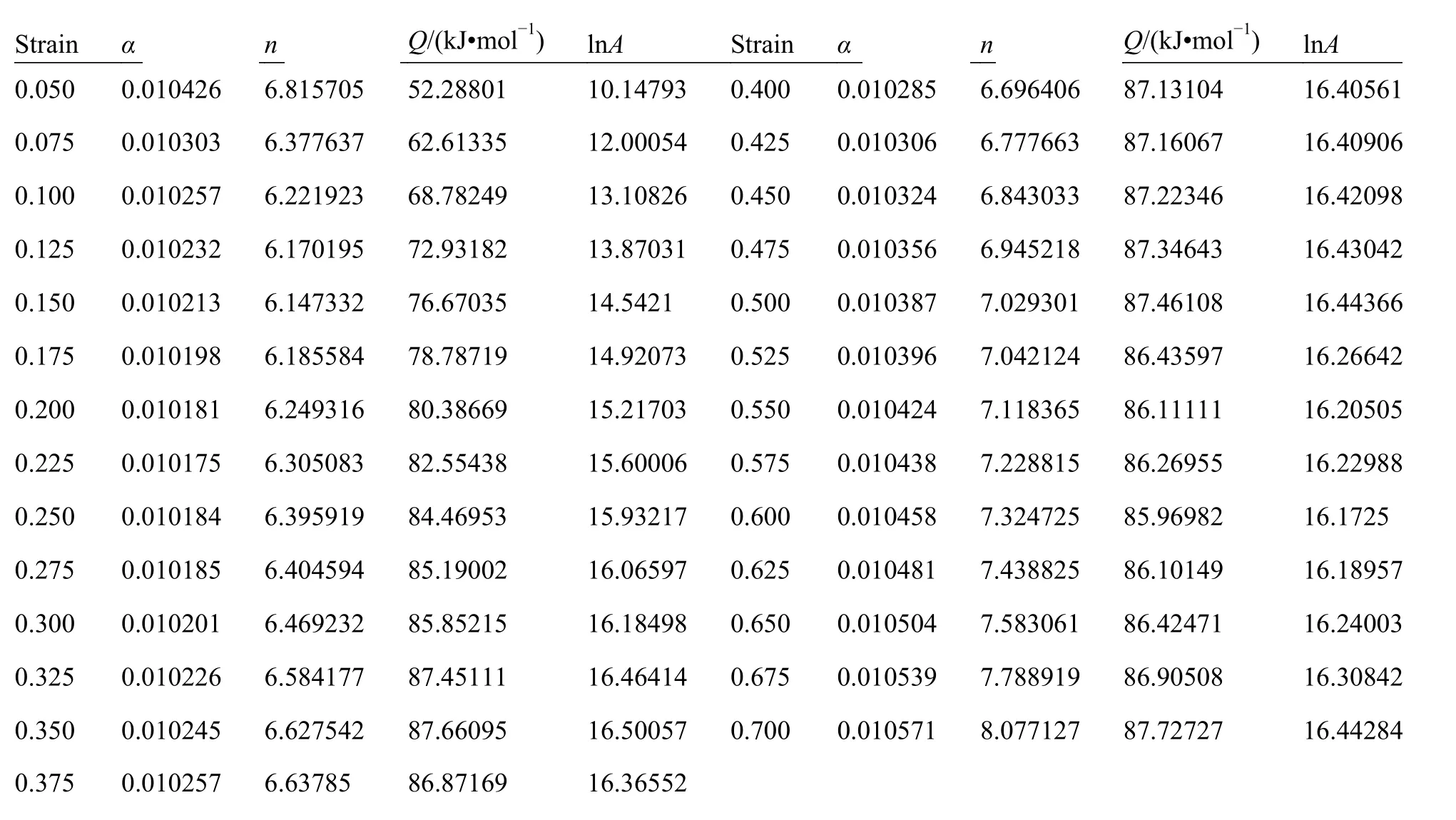
表 2 材料常數與應變量關系數據表Table 2 Relationship between material constant and true strain

通過上述耦合應變量處理后的本構方程模型，再代入相應的T、、ε值，即可獲得該合金在不同變形條件下的流變應力預測數值。其預測數值與實驗數值對比圖象如圖5所示。圖象整體呈現出較高的預測正確性。然而在高應變速率如圖5（b）中的425 ℃，20 s-1下預測值偏低，在圖5（c）中的1 s-1的應變速率下，變形初始階段紅圈所指處預測精確率浮動較大。這是由Arrhenius本構方程的固有數理模型缺陷所造成的，使得非線性預測無法達到更高的精度值。

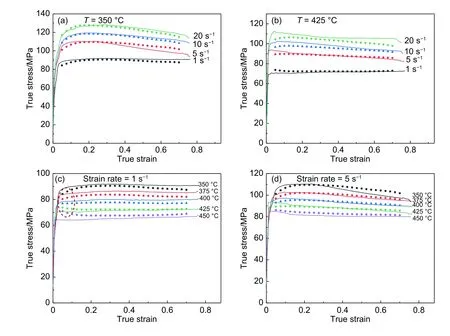
圖 5 不同變形參數下Arrhenius本構方程預測結果Fig. 5 Prediction results of Arrhenius constitutive equation with various deformation parameters（a）350 ℃；（b）425 ℃；（c）1 s-1；（d）5 s-1；

2.3 BP人工神經網絡型本構模型

BP人工神經網絡（BP-ANN）是當下計算機科學領域所流行的算法之一。將BP-ANN模型應用于合金本構方程的構建，利用其誤差反饋自修正的特點能夠有效提高非線性流變應力預測的準確性[18]。BP-ANN由輸入層、隱含層以及輸出層這三個部分構成，其模型結構圖如圖6所示。在輸入層部分，需插入三個神經元節點：T、、ε。輸入層數據經函數傳遞至隱含層后，隱含層對其進行網絡化計算，最終通過函數傳遞至輸出層，得到流變應力σ數值。若在輸出層得不到精準預測的結果，則該模型會進行反向傳播，將誤差信號沿著各神經元節點返回傳遞[19]。其間各神經元權值將受到修改，經過不斷迭代，最終達到理想精度的信號輸出，即訓練過程結束。

研究表明，隱含層的節點數表示該網絡的數據處理能力。節點數的多少決定該模型反饋算法的準確程度[20]。本研究中對隱含層節數為8～20的情況均作出嘗試，發現對于該合金，節點數的多少對于預測準確度來說影響不大。故綜合考慮模型預測準確度與計算機計算能力，將隱含層節點數定為15個，即采用3 × 15 × 1的網絡結構。

此外T、、ε數量級相差較大，若以原數值輸入網絡模型，必然會削弱小數量級參數、ε在模型運算中的權值，影響到模型的收斂速度和預測精度[21]。故在進行運算前，需對上述參量進行歸一化處理，本工作采用mapminmax算法，其公式如式（4）所示。

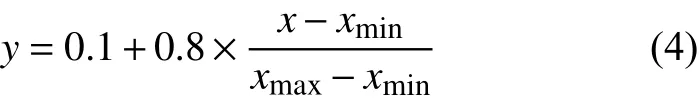
式中：y為歸一化后的T、、ε參數值；x代表各T、、ε參數值；而xmin為參數的最小值；xmax為參數的最大值。通過該式可使得參量初始值控制其范圍在0.1～0.9之內。而后利用MATLAB軟件完成上述模型的構建，其中兩次傳遞過程分別通過Tansig函數和Purelin函數實現，訓練函數為Trainlm，目標精度設為10-5，網絡學習率設為10-4。

圖 6 神經網絡模型結構圖Fig. 6 Structure diagram of neural network model

圖7為BP-ANN模型的流變應力預測結果，由圖7可以看出，紅圈標記部分顯示在變形初始階段預測值略微偏離實際實驗值，這是由于該模型采用固定應變步長所造成的。在加工硬化階段，應力數據點密集，采取更小的步長能夠增加該階段的預測準確率。在初始形變階段后，流變應力預測在穩態應力階段均顯現出超高的預測準確性。

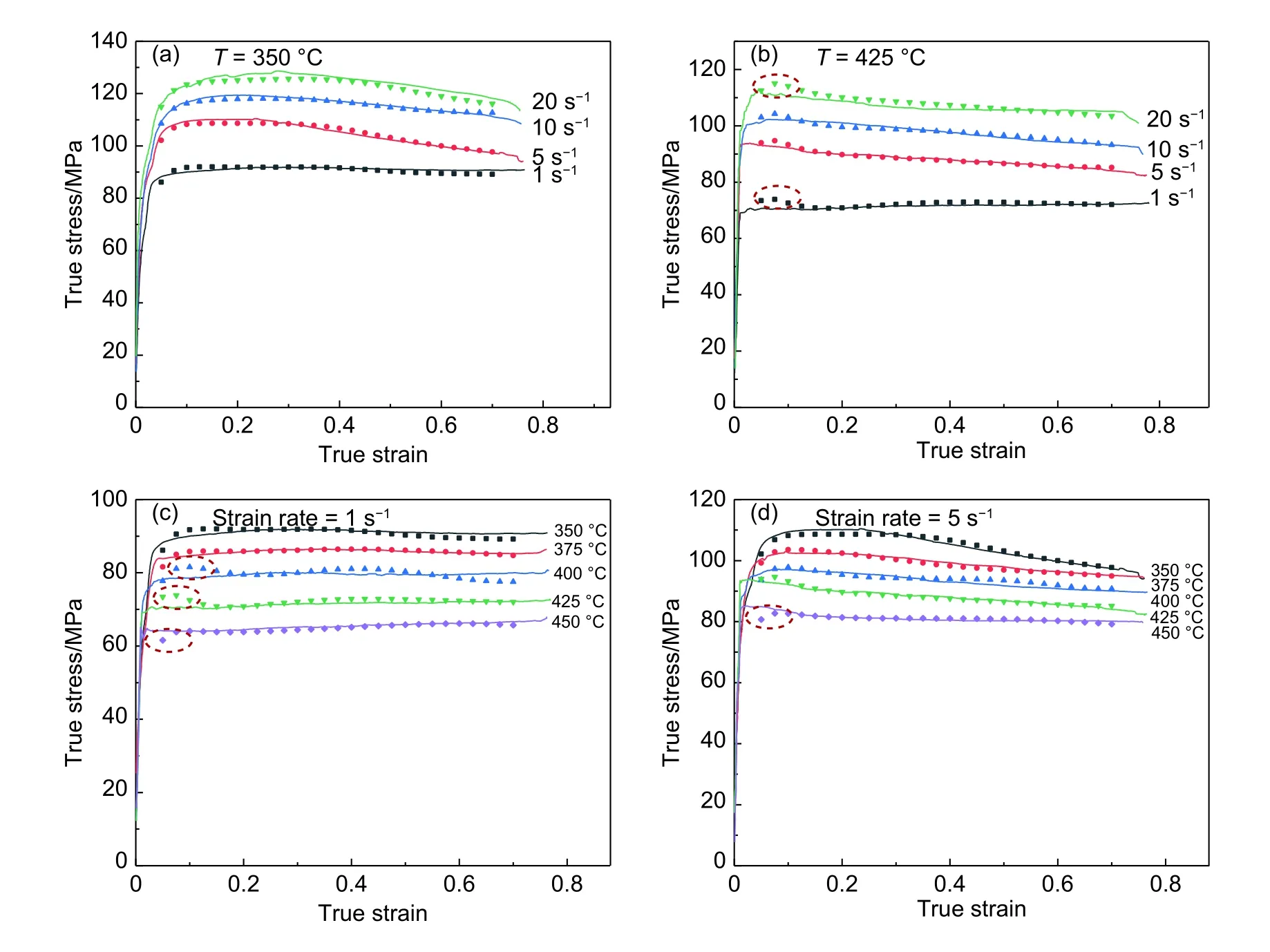
圖 7 不同變形參數下BP神經網絡本構方程預測結果Fig. 7 Prediction results of neural network constitutive equation with various deformation parameters（a）350 ℃；（b）425 ℃；（c）1 s-1；（d）5 s-1；

2.4 本構模型預測對比

對于Arrhenius模型與BP-ANN模型，本文利用通用平均相對誤差δ與相關性系數R2對模型精度進行對比。其計算公式分別如式（5）、（6）所示。

式中：Ei為實驗流變應力值，為其平均值；Pi為模型預測流變應力，為其平均值；N為數據總量。

圖8顯示該兩種模型的整體預測精度對比。圖8所示，BP-ANN模型數據點更加集中，具有更好的預測準確性，其平均相對誤差δ僅為0.813%。而Arrhenius模型的δ值大于2%，相關系數R2對比同樣顯示BP-ANN模型具有更高的精度。從圖9的殘差分析中不難發現，兩種模型在中等應變量0.3～0.5附近時，均具有極高的預測準確度，在此范圍以外均有不同程度的浮動。BP-ANN模型的殘差保持在 ± 4.5 MPa以內，而Arrhenius模型浮動較大，在[-8，-4.5]區間內亦存在較多數據點，預測精度相對較差。

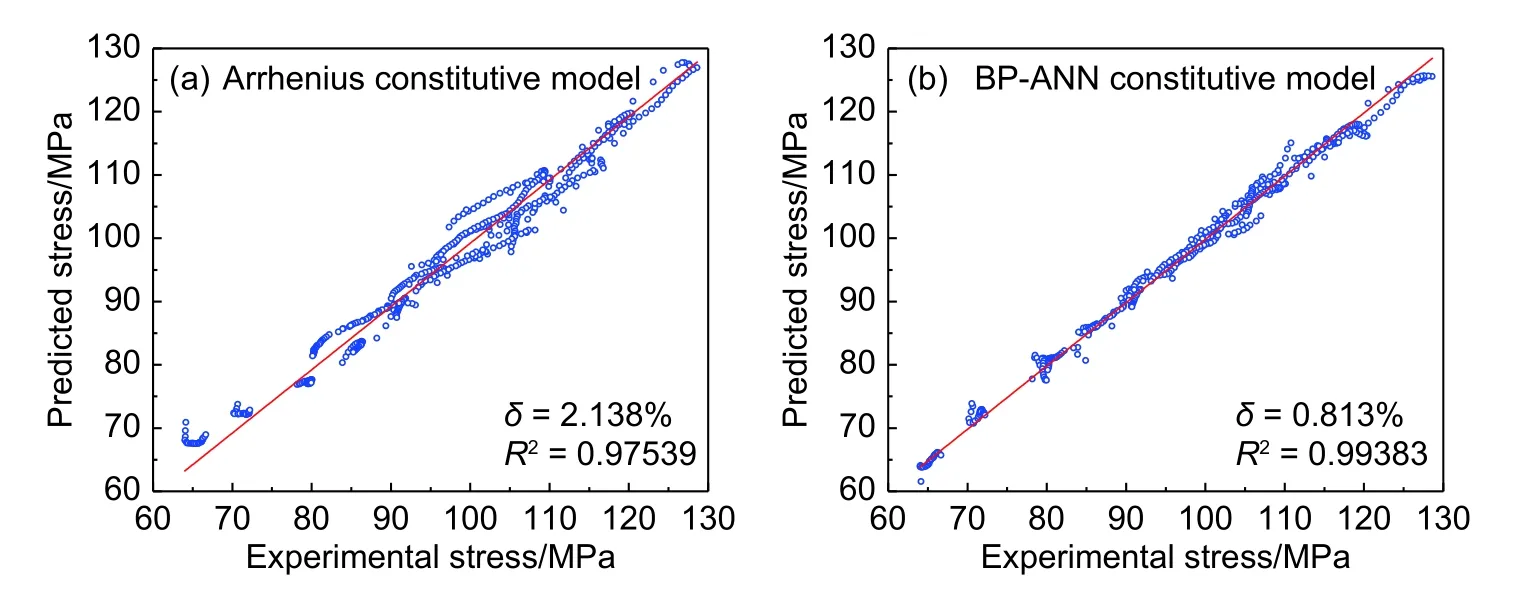
圖 8 不同模型預測應力值的相對誤差與相關性系數對比Fig. 8 Comparison of relative errors and correlation coefficients of prediction stress by different models（a）Arrhenius model；（b）BP-ANN model

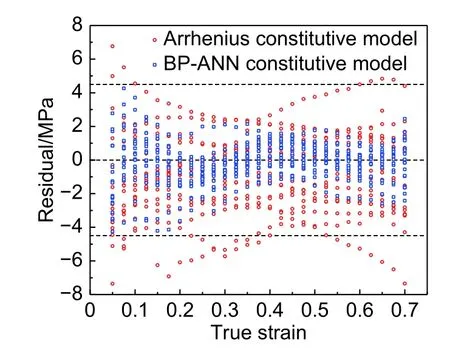
圖 9 唯象型Arrhenius本構模型與BP神經網絡模型殘差對比Fig. 9 Comparison of residual between phenomenological Arrhenius model and BP neural network model

圖10顯示兩種模型平均絕對誤差和平均相對誤差的對比狀況。如圖所示，BP-ANN模型在不同溫度下預測準確度變化較小，穩定性良好。其平均絕對誤差均保持在1.2 MPa的低水平，而平均絕對誤差保持在0.7%～1.05%范圍內。Arrhenius模型的平均絕對誤差在375 ℃時出現極小值，在450 ℃時出現最大值，且平均相對誤差在1.4%～3.5%的較大范圍內浮動。隨著溫度升高，該模型的預測精度總體呈現出下降趨勢。值得注意的是，7系鋁合金的熱加工溫度范圍一般在450 ℃左右，該溫度下強化相狀態將會發生較大改變，MgZn2相易回溶于α-Al基體當中，降低晶界強度，造成沿晶開裂，削弱了合金的可加工性能[22-23]。BP-ANN模型通過反饋傳遞使得本構方程預測在該溫度區間保持較高的準確性。而唯象型Arrhenius本構模型預測的精確度對溫度變化適應性較小，且在450 ℃下相對誤差達到峰值，較難準確預測合金高溫加工性能。綜上所述，對于航空航天用噴射成形7055鋁合金而言，BP-ANN本構模型更能有效描述合金在高溫變形條件下的流變行為。

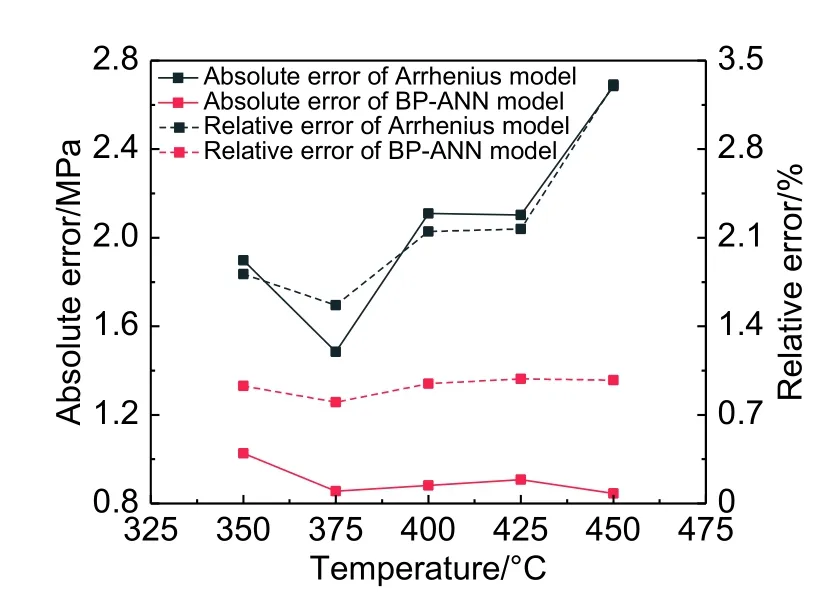
圖 10 模型平均絕對誤差、平均相對誤差與變形溫度的關系Fig. 10 Relationship between average absolute error，average relative error and deformation temperature

3 結論

（1）噴射成形7055鋁合金的流變應力值對變形參數的變化較為敏感，與變形溫度T呈現負相關，而與應變速率呈現正相關。

（2）構建7055鋁合金的耦合應變量的唯象型Arrhenius本構模型及BP人工神經網絡型本構模型。綜合對比上述兩種模型，BP人工神經網絡型本構模型具有更高的預測準確度，平均相對誤差δ值僅為0.813%，而Arrhenius本構模型的δ值大于2%。

（3）BP人工神經網絡型本構模型的流變應力預測具有較高的溫度穩定性。而唯象型Arrhenius型本構模型的預測誤差隨溫度升高總體呈上升趨勢，且在熱加工溫度區間下（450 ℃左右），平均相對誤差達到峰值。