BDS/Galileo/GPS三頻精密單點定位模型比較與分析

卜宇航，李博峰，臧 楠，茍浩洋

（1. 同濟大學 測繪與地理信息學院，上海 200092；2. 哈爾濱工程大學 智能科學與工程學院，哈爾濱 150001；3. 山東省交通規劃設計院有限公司，濟南 250031）

0 引言

全球衛星導航系統（global navigation satellite system, GNSS）的高速發展與革新，為用戶提供了三頻及更多頻率的信號[1-2]。我國北斗衛星導航系統（BeiDou navigation satellite system, BDS）作為全球首個全星座可播發三頻信號的系統，北斗二號（BeiDou navigation satellite（regional）system,BDS-2）已提供了B1I、B2I和B3I的信號服務，為了增強多系統的兼容互操作性，北斗三號（BeiDou navigation satellite system with global coverage,BDS-3）新增了B1C、B2a、B2b和B2a+b四個信號，且未來BDS-2播發的B2I信號將逐漸被BDS-3的B2a信號取代[3]。截止到2019年9月，美國全球定位系統（global positioning system, GPS）發射的12顆Block IIF衛星、在播發L1和L2信號的基礎上，新增了L5信號服務。歐盟伽利略衛星導航系統（Galileo satellite navigation system, Galileo）可播發5個頻率的信號，包括E1、E5a、E5b、E5和E6 。

三頻信號為GNSS精密定位中模糊度固定、周跳探測和快速收斂等問題開拓了新的解決方案[4-7]。精密單點定位（precise point positioning, PPP）技術，因具備操作靈活、成本低且精度高等特點，已成為廣泛應用的GNSS精密定位技術之一[8]。傳統PPP是圍繞雙頻定位模型展開的，隨著多頻信號的播發，三頻PPP的研究及定位性能的評估對多頻PPP的發展具有十分重要意義。目前，三頻PPP的研究也取得了一定的進展。文獻[9-10]利用GPS Block IIF衛星信號，展開了關于三頻PPP算法的研究，指出為了充分利用三頻觀測值，必須考慮頻率間的偏差影響。文獻[11]提出了3種三頻PPP模型，實驗結果表明，三頻PPP較傳統雙頻PPP可縮短約10%的收斂時間，當收斂后，二者定位精度相當。文獻[12]基于全球大量測站的GPS單系統數據，進行了三頻實驗，研究表明，受噪聲系數以及待估參數的不同影響，三頻PPP定位模型間存在性能差異。文獻[13-14]基于BDS三頻數據也展開了相關三頻PPP定位算法等研究。目前大部分文獻僅針對BDS或GPS單系統三頻PPP定位性能評估，關于多系統組合三頻PPP定位性能，以及多系統組合對BDS單系統定位性能的提升尚有待深入研究。因此，本文首先通過合理參數化，推導了2種滿秩可估的三頻PPP函數模型，包括非差非組合模型和雙無電離層組合模型，并給出了2種模型拓展到多系統中的具體表達。隨后采用BDS、GPS和Galileo 三系統觀測數據對2種三頻PPP模型的定位性能進行了評估。

1 三頻PPP定位模型

1.1 GNSS觀測方程

令接收機為r、衛星為s，則載波相位Φ和偽距P的觀測方程[15]為

式中：下標j為頻率編號為衛星與測站之間的幾何距離；對流層延遲為頻率f1的斜路徑電離層延遲，為頻率相關的電離層延遲因子；dtr和sdt分別為接收機鐘差和衛星鐘差；Bj,r和分別為頻率fj上的接收機和衛星相位硬件延遲；Dj,r和分別為頻率fj上的接收機和衛星的碼硬件延遲；是吸收了接收機與衛星初始相位偏差的模糊度；Φε和Pε為相位和偽距的觀測噪聲，包含了各自多路徑效應等其他未模型化誤差。需要特別注意的是，各表達量均以m為單位。觀測方程中的其他誤差項（如：天線相位中心改正、相位纏繞效應、潮汐負荷變形、相對論效應和地球自轉等）均采用模型改正[16]。

式（1）中的衛星鐘差、接收機鐘差、硬件延遲、電離層延遲及模糊度等參數相關，這勢必導致法方程秩虧。因此，需要通過合理參數化的方式解決參數不可估的問題[17]。為了便于表達，定義參數為

式中：ijα和ijβ分別為頻率fi和fj的無電離層組合系數；分別為衛星端和接收機端的差分碼偏差。

首先，采用德國地學研究中心（Deutsches Geo Forschungs Zentrum, GFZ）提供的精密鐘差產品改正衛星鐘差，其中BDS、GPS、Galileo三個系統解算的基礎頻點分別為B1I/B3I、L1/L2、E1/E5a。由于精密衛星鐘差dtsIF是基于雙頻無電離層組合解算的，吸收了各系統解算基礎頻點的無電離層組合的衛星端碼硬件延遲[18]，即

因此，衛星s的鐘差和頻率fj的衛星端，碼硬件延遲可通過精密鐘差及DCB產品進行改正，即

類似地，接收機鐘差、接收機端碼硬件延遲和電離層參數間存在相關性。為了獨立參數化，參考文獻[17]，定義無電離層鐘差參數為

相對碼延遲參數（relative inter-frequency code bias, RIFCB）δD1j為

顯然，無電離層鐘差dtrIF吸收了無電離層組合的雙頻硬件延遲。采用這兩個參數，則任意頻率的接收機鐘差與其硬件延遲之和，以及電離層參數可表達為：

經過精密產品改正及合理的參數化處理，觀測方程式（1）可表達為

1.2 三頻非差非組合模型

根據基本式（9），則觀測n顆衛星的單歷元三頻非差非組合觀測方程為

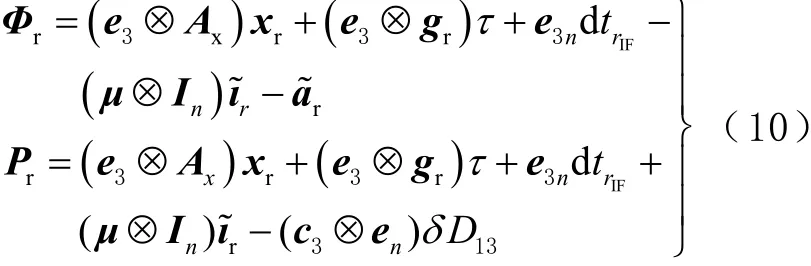
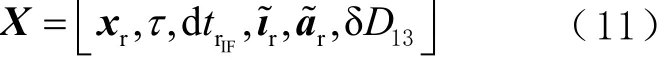
1.3 三頻雙無電離層組合模型

無電離層組合利用電離層延遲的數值特性，通過線性組合消除其一階項的影響。根據等價性原理，每顆衛星的三頻偽距和相位觀測值可構成5個無電離層組合觀測值，其中有一個是由相位和偽距構成的無電離層組合。研究表明，盡管該方式能充分利用所有觀測值信息，但這個相位和偽距構成的無電離層組合帶來的信息增益非常有限，且導致5個無電離層組合觀測值相關，處理相對比較復雜[19]。因此，本文采用三頻偽距和相位觀測值分別構成雙無電離層組合的模型。一般而言，三頻觀測值可以組成三個無電離層組合。各系統采用的三頻觀測值如表1所示，其中BDS在采用B1I和B3I基礎上，BDS-2和BDS-3分別各自采用了B2I和B2b頻點。考慮到噪聲系數的影響，未采用BDS的B2b（B2I）/B3I、GPS的L2/L5和Galileo的E5a/E5b無電離層組合。

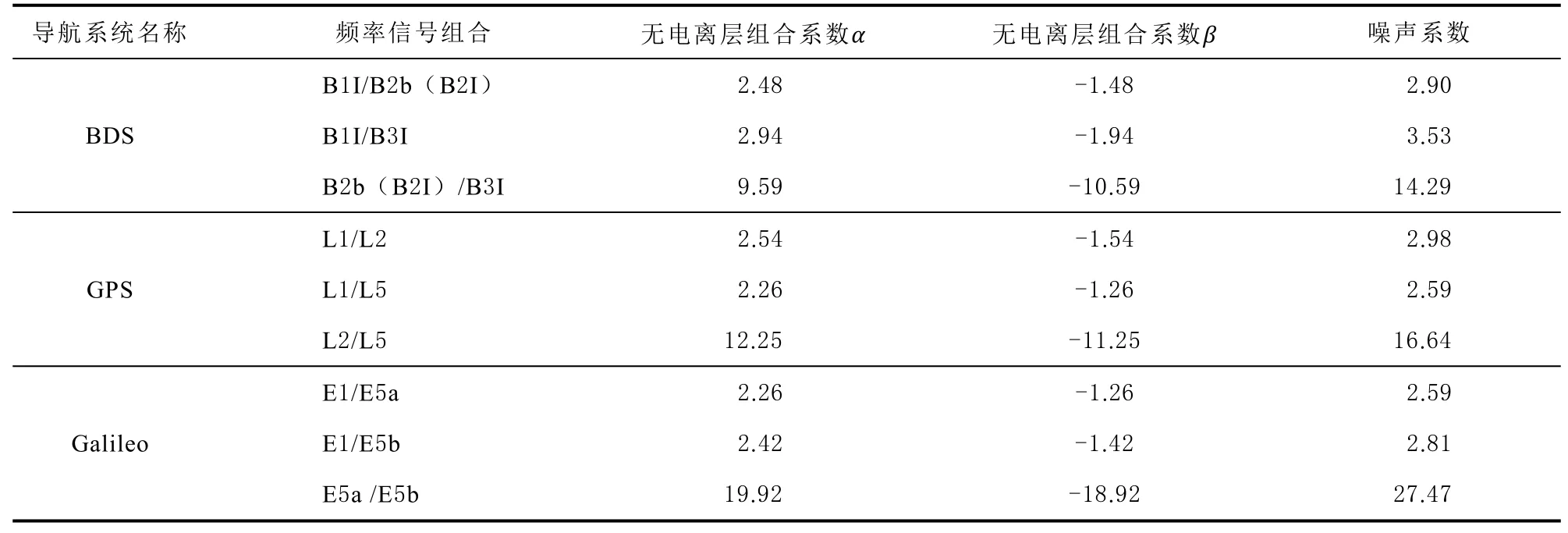
表1 BDS、GPS、Galileo雙頻無電離層組合系數及噪聲系數

三頻雙無電離層組合模型可通過對非差非組合觀測方程（10）左乘一個轉換矩陣3R得到，其中

變換后得三頻雙無電離層組合模型為

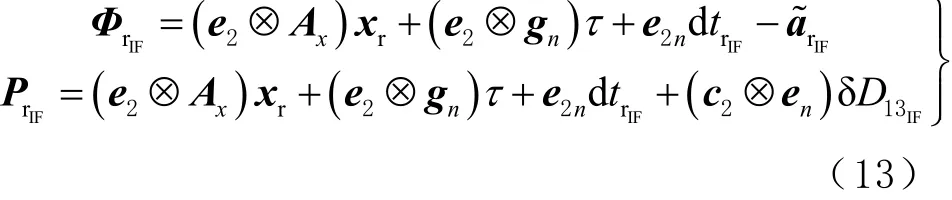
1.4 多系統三頻PPP模型

本文研究的多系統包括BDS、GPS和Galileo。多系統融合的關鍵之一是合理地處理系統間硬件延遲偏差。通常有2種處理方式：一種是每個系統獨立估計各自的接收機無電離層鐘差；另一種是引入系統間碼硬件延遲偏差參數（inter-system code hardware bias, ISCB）[20]，考慮到ISCB的穩定性，從而減少待估接收機無電離層鐘差參數。本文采用引入ISCB參數方式，BDS和Galileo的接收機鐘差為

式中：下標G、C和E分別代表GPS、BDS和Galileo；ηCG=DrIF,C-DrIF,G和ηEG=DrIF,E-DrIF,G分別為BDS和Galileo的ISCB參數，其中DrIF=α12Dr,1+β12Dr,2，為接收機端碼硬件延遲無電離層組合。因此，三系統三頻非差非組合模型為

類似地，三系統雙無電離層模型拓展到多系統為

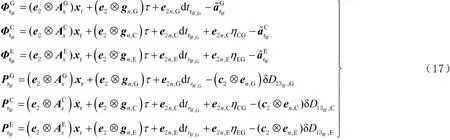
2 三頻PPP的隨機模型

本文采用的相位觀測值天頂方向的觀測精度σ90°為2 mm，相位和偽距觀測值精度比為1∶100。采用衛星高度角函數確定觀測值間關系，則非差非組合PPP隨機模型為

3 實驗與結果分析

3.1 實驗數據及解算策略

選取了12個包含GPS、BDS和Galileo三頻觀測值的國際GNSS服務（International GNSS Service, IGS）組織建立的多模GNSS實驗跟蹤網（multi-GNSS experiment, MGEX）測站，測站分布如圖1所示，數據選取了2019年年積日第121—130天共10 d數據，數據采樣間隔為30 s。分別利用BDS單系統和三系統組合的三頻和雙頻觀測數據進行靜態和模擬動態實驗。

圖1 實驗所選取的12個IGS MGEX觀測站分布

為了充分評估雙頻和三頻PPP不同定位模型在靜態和動態模式下的性能，采用4種評估方案：①雙頻非差非組合模型（DF-UC）；②雙頻無電離層模型（DF-IF）；③三頻非差非組合模型（TF-UC）；④三頻雙無電離層組合（TF-DIF）。

針對這4種方案，采用定位精度和收斂時間兩個指標分析了BDS單系統與三系統組合定位效果，收斂條件為三個方向同時達到收斂閾值且連續60個歷元（采樣時間為30 min）均穩定在閾值內，以IGS中心SINEX文件中的坐標作為各測站的參考坐標。具體的PPP數據處理策略如表2所示。

表2 實驗數據PPP處理策略

3.2 靜態PPP實驗

3.2.1 BDS定位性能分析

圖2給出了2019年年積日第124天FFMJ、LEIJ和ULAB三個測站BDS單系統可視衛星數目與位置精度衰減因子（position dilution of precision,PDOP）值隨時間變化情況。FFMJ與LEIJ測站位于歐洲中高緯度地區，觀測的地球靜止軌道（geostationary Earth orbit, GEO）與傾斜地球同步軌道（inclined geosynchronous orbits, IGSO）衛星數較少，導致PDOP值較差；且隨中圓地球軌道（medium Earth orbit, MEO）衛星數量的變化，數值波動較大。圖3為BDS靜態PPP雙頻和三頻2種模型在E、N和U方向以及3維點位的誤差序列。在定位初始化階段，同一時刻2種模型的三頻PPP定位性能相比于雙頻均有明顯提高，可視衛星幾何分布較差的FFMJ與LEIJ測站改善效果更加明顯。

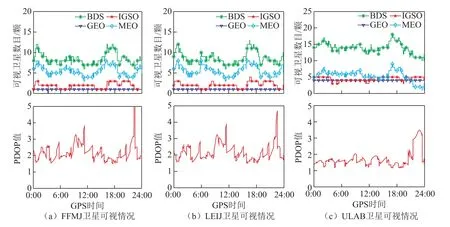
圖2 FFMJ、LEIJ和ULAB測站可視的BDS可視衛星數目與PDOP值

圖3 FFMJ、LEIJ和ULAB測站BDS單系統靜態PPP定位誤差（0時至4時）

圖4給出了4種方案所有測站連續10 d收斂至不同閾值的單天解均方根（root mean square,RMS）和收斂時間的平均值。當收斂閾值為0.1 m時，DF-UC模型E、N和U三個方向RMS分別為1.62、1.18和4.19 cm；TF-UC模型為1.42、1.05和3.87cm，提升約12.3%、11.0%和7.6%。DF-IF

圖4 BDS單系統靜態PPP四種方案不同收斂閾值單天解RMS和收斂時間平均值

模型E、N和U三個方向RMS分別為1.28、0.95和2.33 cm，TF-DIF模型分別為1.14、0.86和2.18 cm，提升約10.6%、9.1%和6.4%。從定位精度角度比較三頻相比于雙頻的提升，TF-UC模型略優于TF-DIF模型。當收斂閾值達到0.1、0.5和1 m時，TF-UC較DF-UC模型分別提高了10.0%、10.4%和16.4%；TF-DIF較DF-IF模型分別提高了13.7%、16.4%和18.3%。從收斂時間角度比較三頻相比于雙頻的提升，三頻PPP可有效縮短收斂時間，尤其是初始化收斂階段并且TF-DIF模型優于TF-UC模型。

從以上算例可以分析得出：由于TF-UC模型待估參數較多且參數之間存在一定時空相關性；因此導致在初始收斂時間方程性態差，收斂時間長。TFDIF模型由于組合觀測值之間的相關性導致該模型在定位精度上提升不如TF-UC模型明顯。

3.2.2 三系統組合定位性能分析

圖5給出了FFMJ、LEIJ和ULAB三個測站三系統組合的可視衛星數目與PDOP值。三系統組合的PDOP值在1左右，顯著小于BDS單系統，即多系統組合有效改善了可視衛星的空間分布幾何構型。圖6展示了上述三個測站靜態PPP四種方案的定位誤差，由圖看出三頻略優于雙頻定位結果，較BDS單系統有明顯提高。

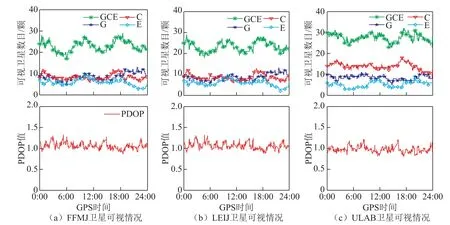
圖5 FFMJ、LEIJ和ULAB測站可視的三系統可視衛星數目與PDOP值

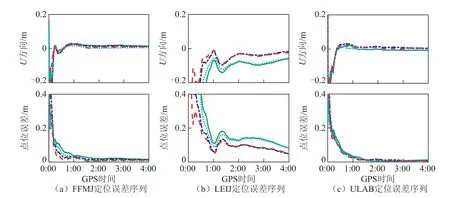
圖6 FFMJ、LEIJ和ULAB測站三系統靜態PPP定位誤差（0時至4時）

圖7統計了三系統組合的4種PPP方案所有測站連續10 d收斂至不同閾值的單天解RMS定和收斂時間的平均值。當收斂閾值為0.1 m時，DF-UC模型在的E、N和U三個方向的RMS分別為0.82、0.55和1.23 cm，TF-UC模型為0.71、0.49和1.13 cm，相對提升了13.4%、10.9%和8.0%。DF-IF模型三個方向RMS分別為0.81、0.53和1.07 cm，TF-DIF模型分別為0.72、0.48和1.02 cm，對應提升了11.1%、9.1%和4.6%。三系統組合與BDS單系統相比，三個方向的TF-UC模型分別提高了50.0%、53.3%和70.8%，TF-DIF分別提高了36.8%、44.2%和53.2%。由圖7（b）得出收斂至0.1 m時，三系統組合的TF-UC和TF-DIF模型僅需21.7 min和18.6 min，較BDS單系統分別提高了77.6%、78.6%。但是就三系統組合而言，三頻較雙頻的收斂時間提升不明顯，這主要是因為三系統組合的衛星數目充足且分布合理，PDOP值得到了極大改善，使得三頻對收斂時間的增益有限。

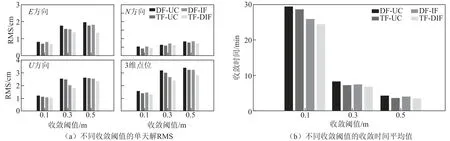
圖7 三系統組合靜態PPP四種方案在不同收斂閾值下的單天解RMS和收斂時間

3.3 模擬動態PPP實驗

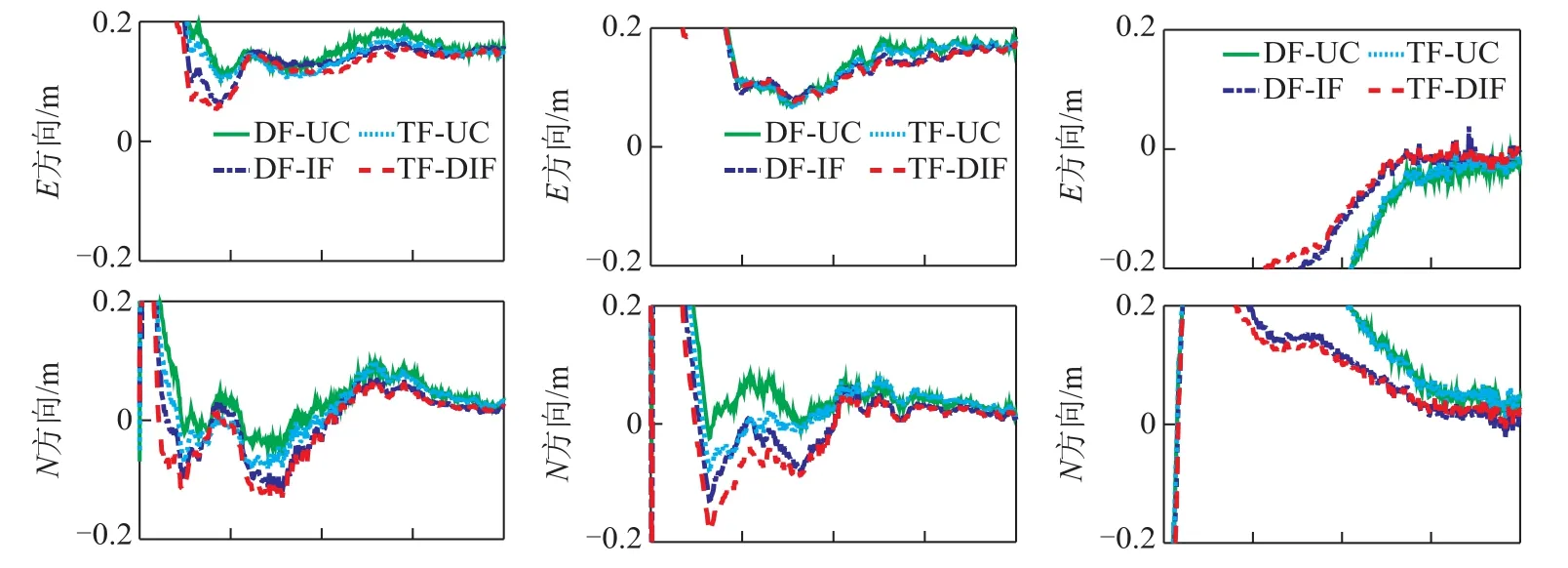
圖8給出了BDS單系統FFMJ、LEIJ和ULAB三個測站動態PPP在（0:00—4:00）時段E、N和U三個方向以及3維點位的誤差序列圖。在初始化階段，三頻TF-UC和TF-DIF模型較雙頻模型具有更高的定位精度。

圖8 FFMJ、LEIJ和ULAB測站BDS單系統動態PPP定位誤差（0時至4時）

圖9給出了三系統組合動態PPP的定位誤差，相較于BDS單系統，三系統組合動態定位結果更加穩定，收斂更快。

?

圖9 FFMJ、LEIJ和ULAB測站三系統組合動態PPP定位誤差（0時至4時）

表3 BDS單系統動態定位性能統計

表4 三系統組合方案動態定位性能統計

表3和表4分別統計了12個測站10 d數據BDS單系統和三系統組合定位三個方向同時收斂至0.1 m的RMS和收斂時間。結果表明，BDS單系統和三系統組合三頻定位模型結果在三個方向上的定三精度和收斂時間均優于雙頻模型定位結果。三系統組合的三頻TF-UC模型三個方向精度分別為1.42、1.03和2.89 cm，相比BDS單系統提高了39.1%、51.2%和44.8%。三系統組合三頻TF-DIF模型三個方向精度分別為1.36、0.97和2.81 cm，相比BDS單系統提高了41.8%、53.6%和45.9%。同時，三系統組合三頻定位模型相比BDS單系統三頻定位模型的收斂時間顯著縮短，TF-UC模型的收斂時間從144.5縮短至24.0 min，TF-DIF模型的收斂時間從123.7縮短至22.8 min，分別提高了83.4%、81.6%。

4 結束語

本文從基本觀測方程出發，詳細地介紹了2種三頻PPP定位模型：非差非組合模型和雙無電離層組合模型。通過實驗，從定位精度與收斂時間2個角度比較與分析得出以下結論：

1）在衛星分布較少、PDOP值較差的情況下，三頻PPP相比雙頻PPP可以有效提高定位結果的精度與可靠性，尤其是在定位初始階段。

2）相較于雙頻PPP，三頻PPP兩種定位模型的定位性能均有所提高。定位精度方面，非差非組合模型提升優于雙無電離層組合模型；收斂時間方面，雙無電離層組合模型提升優于非差非組合模型。

3）受益于GPS、Galileo和BDS融合對衛星空間幾何分布構型的改善，三系統組合的三頻PPP定位性能較BDS單系統有大幅度的提升。