多噴管運載火箭底部熱環境研究

閆指江，沈 丹，吳彥森，蒲鵬宇，宮宇昆

（1. 北京宇航系統工程研究所，北京，100076；2. 北京理工大學，北京，100081）

0 引 言

為了獲得更大的推力，運載火箭動力系統常采用多噴管并聯方案，如美國的土星V火箭[1]、蘇聯的能源號火箭、歐空局的阿里安-5火箭、日本的H-ⅡA火箭以及中國的CZ-2F火箭等[2]。在運載火箭上升的過程中，相鄰噴管射流之間、射流與自由來流之間相互作用，在火箭底部形成復雜的循環流動或沖擊反流，使運載火箭底部承受較高的熱載荷[3]。因此，在運載火箭總體設計的過程中，需要預估底部熱流并采取相應的熱防護措施。然而，由于運載火箭底部流動極為復雜，理論分析方法與實際的遙測結果相比偏差較大；同時，由于縮比效應以及測量的不確定性，試驗數據難以直接用于底部熱流的預估[3,4]。因此，有必要建立相應的數值模型對火箭底部熱環境進行仿真分析，明確底部流動結構以及各種因素對底部熱流的影響，最終為底部熱防護設計提供參考。

Hideyo等[5]采用密度基隱式求解器求解耦合了realizablek-ε湍流模型[6]的N-S方程，同時采用P-1輻射模型[7]求解輻射傳熱，得出了H-ⅡA火箭包含噴管射流在內的流場以及底部壁面熱流分布。Mehta等[8]采用SST-kω與BSL-kω（Baseline）湍流模型對Musial等[9]所做的四噴管火箭縮比模型風洞試驗進行了數值計算，分析對比了四噴管火箭底部熱環境對不同數值模型的靈敏度。Patel等[10]在此基礎上采用BSL湍流模型對兩噴管構型的Antares運載火箭底部熱環境進行了數值計算，并考慮了燃氣回流后在底部區域的復燃。喬野、聶萬勝等[11]對火箭模型進行了簡化，僅考慮火箭尾端及噴管部分，采用耦合了Realizablek-ε湍流模型的N-S方程描述尾焰流動過程，考慮復燃反應的影響，得到不同飛行高度下火箭動力系統的尾焰流場結構。

目前為止，國內外對芯級為兩噴管構型并捆綁助推器的運載火箭底部熱環境的分析研究還較少，且缺少對火箭側壁面邊界層流動分離規律的研究。本文以芯級兩噴管加四助推器火箭為研究對象，對其周圍流場域進行了網格劃分，采用密度基隱式求解器對耦合了SST湍流模型的N-S方程進行求解，擬得出火箭底部熱環境特性，為運載火箭底部熱防護設計提供參考。

1 物理模型和計算方法

1.1 物理模型

幾何模型如圖1所示，由直徑為3.35 m的芯級火箭和4個直徑為2.25 m的助推器組成，4個助推器按旋轉90°分布。芯級火箭底部裝有2臺發動機，每臺發動機噴管向外偏轉2°；每個助推器底部裝有1臺發動機，發動機噴管向外偏轉6°。

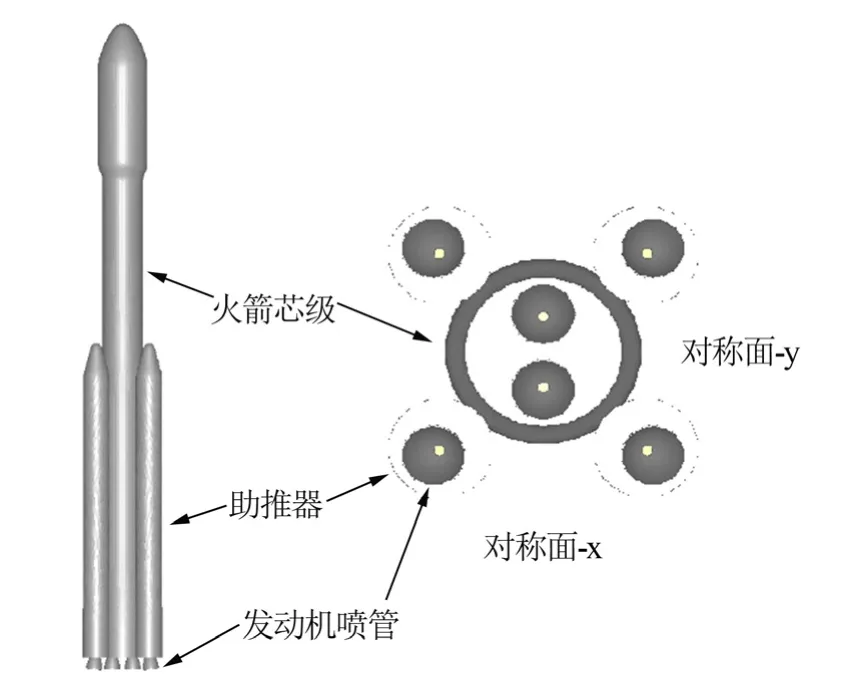
圖1 多噴管火箭的幾何模型Fig.1 Geometric Model of the Multi-nozzle Rocket

本文研究的運載火箭發動機為液氧/煤油型，噴管出口燃氣比熱比為1.16，喉部與出口面積比為1∶35，喉部直徑約為200 mm。液氧/煤油發動機性能參數如表1所示，其中，Tinlet與Pinlet分別為推力室總溫與總壓；Cp與μ為推力室燃氣定壓比熱與動力粘性系數。

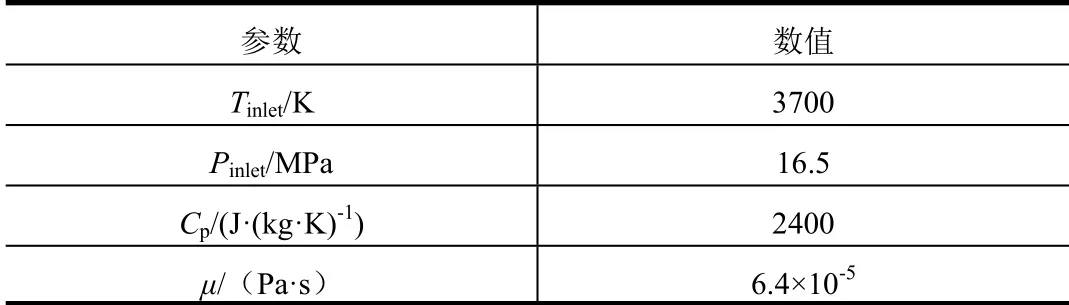
表1 火箭發動機性能參數Tab.1 Parameters of Rocket Engine Performance

1.2 計算模型

根據文獻[8]的計算經驗，采用SST模型[12]與BSL模型所得出的底部熱流數據相差小于2%，而SST模型能夠更好地反應逆壓梯度下的流動分離現象，因此本文選取SST湍流模型用于仿真計算。同時，根據文獻[8]的結果，采用等效燃氣與空氣雙組份混合模型計算得出的熱流比采用多組分有限速率化學反應模型計算結果更高，從工程安全要求與提高計算效率綜合考慮，采用雙組分混合氣體模型計算是合理的。

1.3 控制方程求解

控制方程采用時間推進的隱式方法求解，該方法具有較強的穩定性。應用有限體積法離散噴管內部和火箭周圍流場控制方程，對流項采用二階迎風格式、擴散項采用中心差分格式構建差分方程，梯度采用基于單元中心的最小二乘法獲得，采用Roe格式[13]對單元面上的通量進行離散，最終采用Gauss-Seidel迭代結合代數多重網格方法[14]對離散后的代數方程組進行求解。

1.4 網格劃分與邊界條件

根據幾何模型的對稱性，選取1/4模型以提高計算效率。為了便于局部網格加密，采用非結構四面體網格對邊界層外流場區域進行網格劃分。為了準確模擬運載火箭的底部流動結構，在底部區域進行了網格加密。為了模擬火箭側壁面流動分離，準確計算火箭壁面熱流，采用棱柱網格解析邊界層內流動，確保第一層網格中心處計算網格與邊界條件如圖2所示，網格總量為570萬。不同飛行高度對應邊界條件設置如表2所示，其中，Ma∞、p∞、T∞分別代表來流馬赫數、靜壓與靜溫，10.5 km與26 km為低海拔工況，45 km與62 km為高海拔工況。除噴管內壁面與噴管邊緣為絕熱壁面外，其余壁面均保持恒溫330 K。

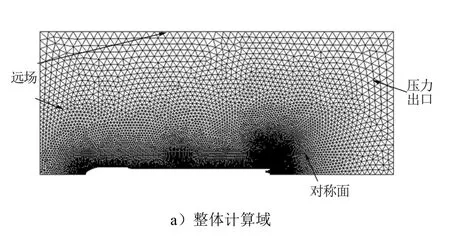
圖2 網格模型和邊界條件Fig.2 Mesh and Boundary Conditions

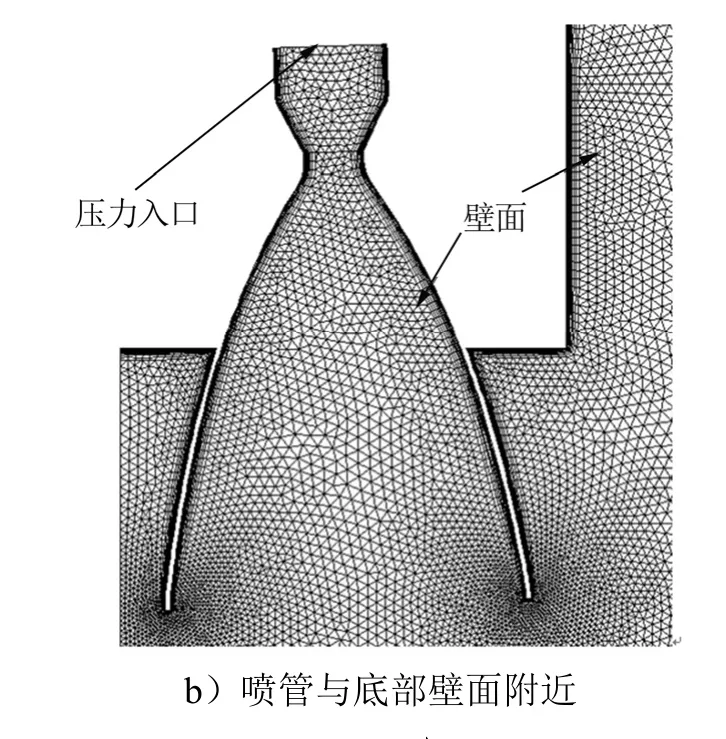
續圖2

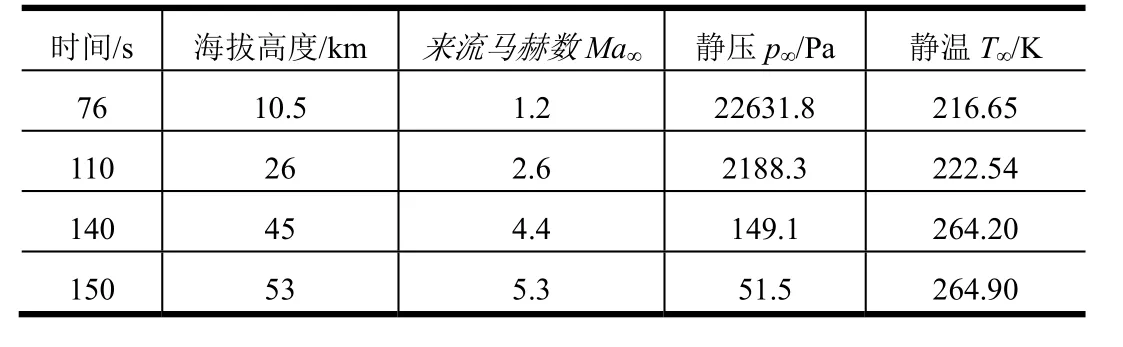
表2 邊界條件選用參數Tab.2 Boundary Conditions Selection Parameters

1.5 計算方法驗證

為了驗證數值計算方法的有效性，選取文獻[8]中用于對比驗證的四噴管火箭縮比試驗工況[9]進行數值仿真計算。該試驗將四噴管火箭縮比模型安裝在風洞中模擬真實來流條件下火箭發動機穩定工作過程，通過傳感器測量火箭模型底盤上的熱流密度分布。圖3顯示了選取的試驗工況下數值計算結果與試驗數據的對比。由圖3可知，二者反映的熱流密度沿底部半徑的分布規律具有較高的一致性，說明選取的數值計算方法能夠較好地反映多噴管運載火箭底部熱環境特性。

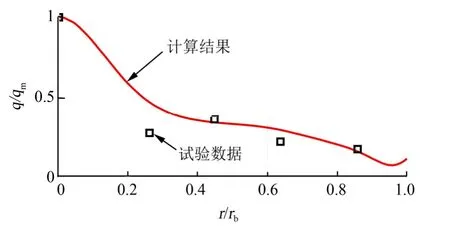
圖3 底部熱流延徑向分布對比Fig.3 Comparison of Base Heat Flux Distribution

2 計算結果分析

運載火箭底部流動受其整體幾何外形的影響。圖4為不同飛行高度下火箭周圍流場馬赫數云圖。如圖4a所示，在飛行高度較低時，來流馬赫數較低，箭體對來流的阻擋效應不明顯。隨著飛行高度升高，來流馬赫數增大，在箭體頭部形成弓形激波，波后流速降低，壓強與溫度升高，從而與遠場來流條件產生差異，進而影響底部流動。由圖4d可知，高海拔工況下火箭底部上游出現亞聲速區，此時底部流動與上游來流相互影響，故箭體外形對底部流動的影響不可忽略。因此，保留全箭模型進行仿真計算對于準確反映火箭底部流動是必要的。此外，相比芯級頭部，助推器頭部距底部更近，因此其產生的激波能夠更為直接地干擾尾焰流場，對底部流動的影響更大。

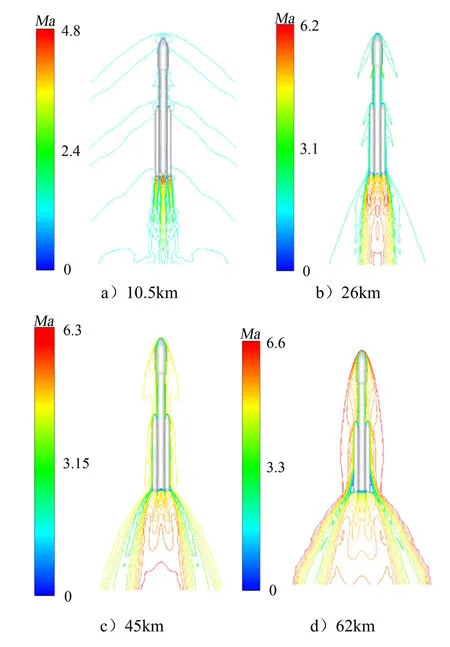
圖4 尾焰流場馬赫數云圖Fig.4 Wake Flow Field Mach Contour

尾焰射流膨脹角決定了火箭底部流動結構，進而影響底部壁面熱流分布。由圖4可知，隨著飛行高度的升高，環境壓強降低，燃氣射流逐漸從過膨脹狀態發展為高度欠膨脹狀態[15]。

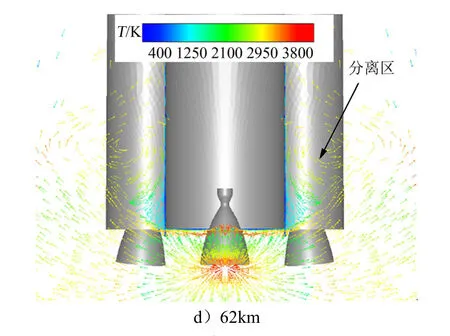
不同飛行高度下火箭底部流動矢量如圖5所示。低海拔工況下，射流膨脹角較小，射流間碰撞較弱，而來流動壓較大，此時射流混合邊界層內一部分動量較小的燃氣相互碰撞后向底部流動，在來流的剪切作用下形成循環流動，在一定高度范圍內隨著飛行高度升高，底部沖擊區逐漸從中心向外移動；而在高海拔工況下，射流膨脹劇烈，來流動壓較低，因此相鄰噴管射流碰撞后直接從碰撞點反向沖擊火箭底部，并阻擋動壓較低的來流空氣流入底部區域。此時沖擊區集中在底部中心處。從火箭底部近壁面流場溫度可以看出，高海拔工況底部近壁面流場溫度高于3000 K，遠高于低海拔工況，說明高海拔工況下火箭底部的流熱環境更為惡劣。

圖5 流動矢量的溫度云圖Fig.5 Flow Vectors Colored by Temperature

續圖5

芯級火箭底部熱流密度分布隨飛行高度的變化如圖6所示，圖中熱流峰值區位置與圖5中的沖擊區對應，熱流峰值大小取決于高溫氣體沖擊強度，即氣流密度與沖擊速度。低海拔工況下，高溫氣體對底部的沖擊強度較低。隨著飛行高度升高，熱流峰值區從底部中心向邊緣移動，熱流逐漸升高。而高海拔工況下高溫氣體沖擊強度較高，峰值大小為低海拔工況的2～10倍，熱流峰值區集中在底部中心。相比于45 km工況，62 km高度下底部熱流密度峰值有所下降，這是由于62 km工況下環境壓強較低，底部高溫沖擊氣流更為稀薄，使得高溫氣體沖擊強度下降，從而降低了底部熱流密度。

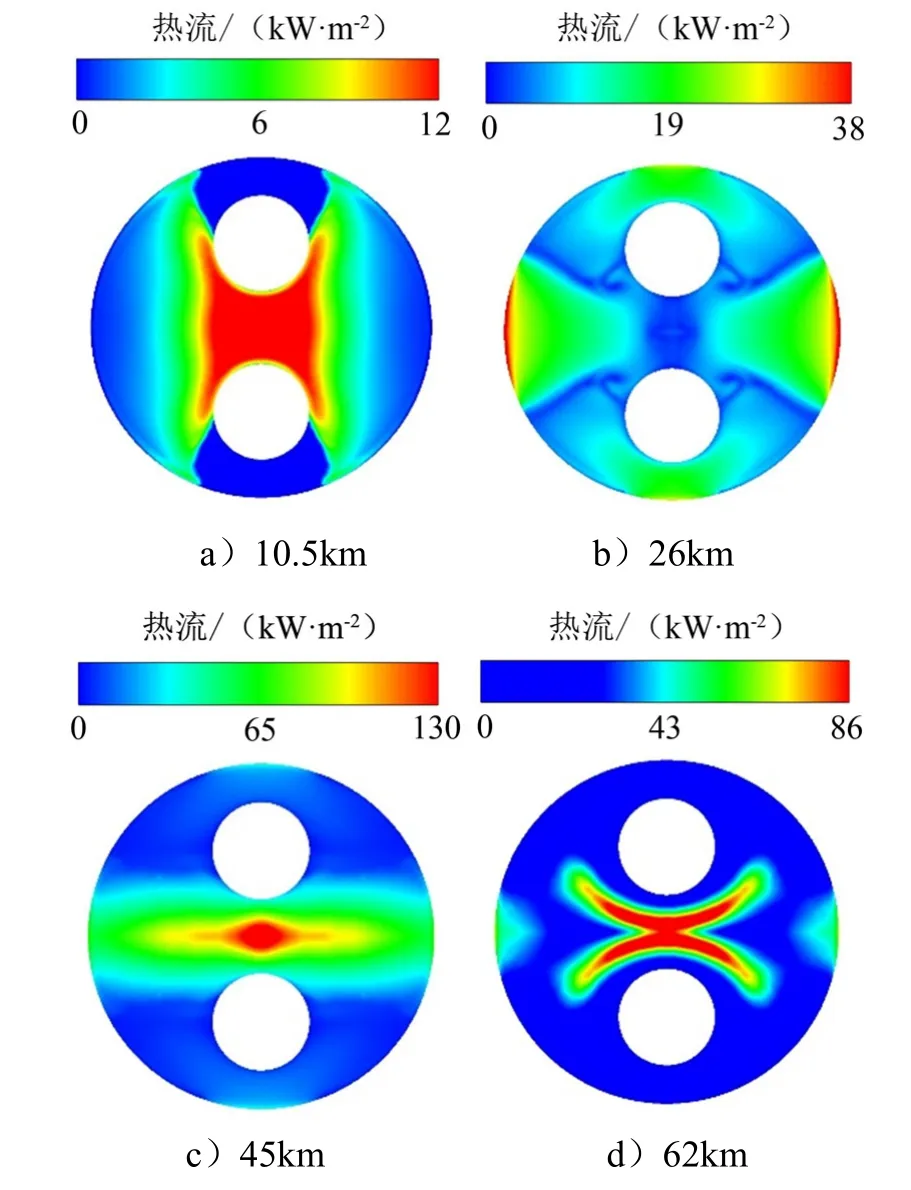
圖6 底部壁面熱流分布Fig.6 Bottom Wall Heat Flux

除增大底部熱流外，射流膨脹角增大還會強化其對來流的阻擋作用，使其上游側壁面產生流動分離。由圖5可知，隨著尾焰射流對來流的阻擋逐漸增強，飛行高度達到26 km時火箭側壁面已出現流動分離，分離臨界高度應位于10.5～26 km之間。流動分離的存在使底部燃氣向上流動填充分離區，加熱火箭側壁面。

由于助推器的阻擋作用，火箭芯級側壁面流動分離主要分布在相鄰助推器之間的區域。定義穿過芯級兩噴管的對稱面為x面，穿過兩噴管之間區域的對稱面為y面，分別獲取兩對稱面內火箭側壁面流動分離點距火箭底面的高度，如表3所示。在同一工況下，y對稱面內分離點位置更高，這是由于在y對稱面內芯級兩股噴管射流相互碰撞，相比于只有單股射流的x對稱面，其對上游來流的阻擋作用更強，產生的逆壓梯度更大，因而分離點更高。對不同飛行高度，分離點位置隨飛行高度升高逐漸上移，這與尾焰射流對來流的阻擋作用隨飛行高度升高而增強是一致的。火箭芯級側壁面熱流密度分布如圖7所示，流動分離區內的高溫氣體顯著增大了火箭側壁面熱流。

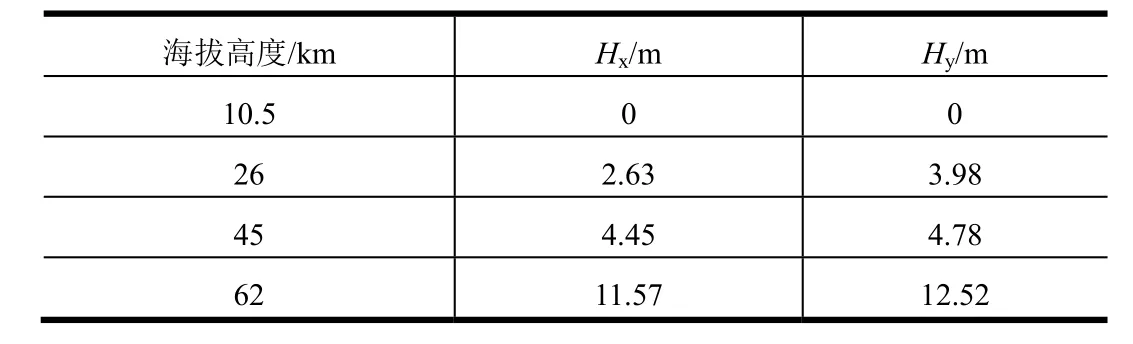
表3 箭體側壁不同位置Tab.3 Different Positions on the Side Wall of the Body

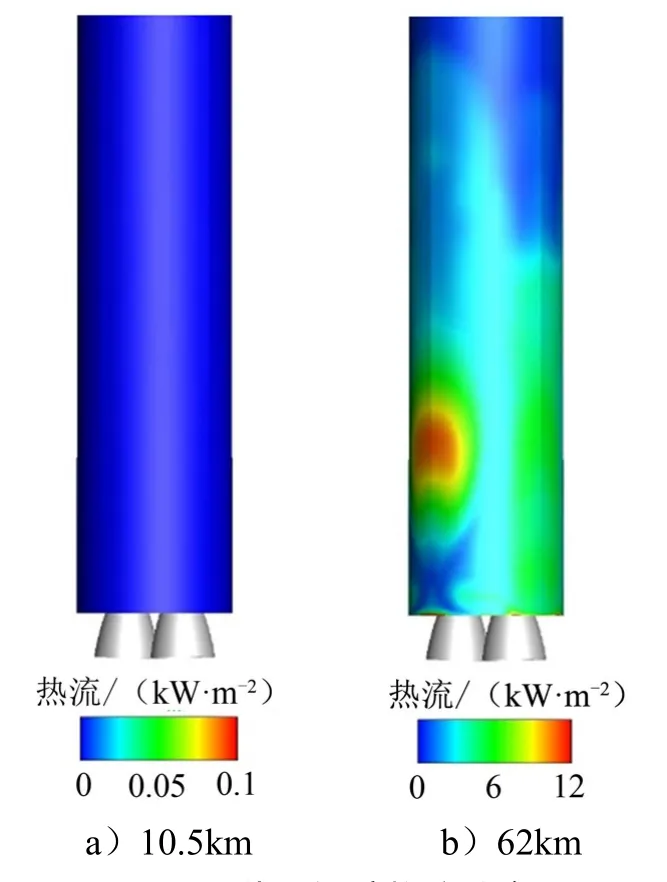
圖7 芯級側壁熱流分布Fig.7 Heat Flux on the Lateral Wall

3 結 論

本文建立了兩噴管芯級加四助推器火箭底部熱環境的數值計算模型，分別研究了10.5 km、26 km、45 km、62 km 4種工況下火箭底部熱環境特性，并分析了火箭側壁面的流動分離現象及其對壁面熱流的影響，得出了如下結論：

a）火箭頭部激波使得波后流動速度降低，增大波后溫度與壓強，從而影響火箭底部流動。相比于芯級頭部，助推器對底部流場影響更大。

b）火箭底部熱流主要由高溫氣體對底部的沖擊強度決定，隨著飛行高度升高，射流膨脹角增大，高溫燃氣對底部的沖擊增強，使得底部熱流密度峰值逐漸增大，在一定高度范圍內峰值區從底部中心向外移動，之后又回到底部中心區域。因此底部熱流隨飛行高度升高先增大后減小，45 km高度下底部熱流最大。

c）尾焰燃氣射流對來流的阻擋作用會導致箭體側壁面邊界層發生流動分離，臨界分離高度在10.5～26 km之間。流動分離使得高溫燃氣加熱箭體側壁面，其中熱流密度最大點位于側壁面底部邊緣處。側壁熱流大小以及流動分離點高度取決于尾焰射流對來流的阻擋作用，射流阻擋作用越強，分離點越高，側壁熱流密度峰值和加熱范圍越大。