新一代運載火箭12點調平控制策略設計及優化

劉麗媛，邢 然，李道平，鄭國昆，李靜妍

（北京航天發射技術研究所，北京，100076）

0 引 言

傳統的發射平臺一般采用4點支撐方式，進行垂直度調整，新一代運載火箭采用12點（以下簡稱多點）支撐的平臺，對平臺支撐物的垂直度調整控制提出了更高精度的要求。多點調平的動作狀態較為復雜，主要包括：4點同升同降，12點同升同降，4點對角垂調，12點對角垂調。在調平過程中要滿足支臂高度、支臂載荷和水平儀監測等多條件約束，增加了控制難度，由于無成熟技術借鑒，需對多點調平控制策略進行研究，尋求多條件的相互協調。

根據需求，調平時跟隨精度和載荷控制要求在一定范圍內，以保證系統總體的安全性。基于試驗需要得到：非線性載荷的變化規律，進行支臂載荷調整時對其它支臂載荷的影響情況，掌握載荷調整控制方法，為研究多點調平的控制方法，進行控制流程的優化提供依據。

本文通過理論分析，并結合試驗的具體情況，對多點調平影響因素與控制算法進行了探討，以實現12點平面下的快速調平閉環控制。

1 理想的調平過程及條件

平臺的12個支撐點分布示意如圖1所示。

圖1 12個支撐點分布示意Fig.1 Distribution Diagram of 12 Support Points

多點調平是希望通過程序的計算控制實現12點1個平面的理想狀態。在M、M1、M2、M3、M45個位置分別安裝1個水平測量儀，由5個測量數據計算加權平均值，根據加權平均值進行水平面的調整。

12點調平的主要動作包括：4個主支承臂同升同降；12個支臂同升同降；4個主支承臂4點對角升降調平（1個主支承臂上升，同時其對角主支承臂下降，即1升1降）；12點支臂升降調平（1個象限內所有支臂上升，同時其對角象限所有支臂下降，即5升5降，各支臂動作過程中保持平臺支撐物作平面翻轉運動）。最終，希望通過各個動作的調整，使得12點處于同一平面，并在調整過程中滿足以下條件：

a）4個主支承臂同升同降時：中間4個主支承臂以I象限主支承臂為基準，在同升過程中其它3個主支承臂與其高度差不超過±0.5 mm，受力接近極限值時暫停，進行載荷調整，載荷調整好后繼續按上述要求同升，要求全過程4個主支承臂位移差小于±0.5 mm，否則報警停止。

b）12個支臂同升同降時：要求與4點情況相同。

c）4個主支承臂對角升降時（以Ⅰ、Ⅲ象限對角升降為例）：各支臂動作過程中，主支承臂Ⅰ為動作基準，主支承臂Ⅲ與其位移偏差小于±0.5 mm。載荷出現偏差時暫停，進行調整后繼續調平。要求全過程4個主支承臂位移差小于±0.5 mm，否則報警，程序停止。

d）12個支臂對角升降時（以Ⅰ、Ⅲ象限對角升降為例），各支臂的支臂速比關系理論位移，如圖2所示。

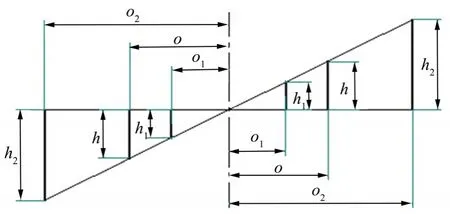
圖2 支臂運動理論位移示意Fig.2 Theoretical Displacement Diagram of Arm Motion

以Ⅰ象限主支承臂為基準，Ⅲ象限主支承臂與其進行反向動作。動作規律是遠端輔助支承臂速度∶主支承臂速度∶近端輔助支承臂速度=1507.6∶850∶443.2，轉換為相應位移比率是遠端輔助支承臂位移（h2）∶主支承臂位移（h）∶近端輔助支承臂位移（h1）=1.77∶1∶0.52。過程中，所有隨動支承臂位移與基準支承臂位移差不超過±0.5 mm，受力接近極限值時進行載荷調整，載荷調整好后繼續運行。要求全過程4個主支承臂位移差小于±0.5 mm，否則報警，程序停止。

外圍8個輔助支承臂隨動控制要求：Ⅰ象限4個支承臂以各自初始設定的速度進行同降，Ⅲ象限4個支承臂以各自初始設定的速度進行同升。其位移與基準支承臂位移（按比例折算值）差不超過±0.5 mm。升降過程中保證支承臂受力在要求范圍內。受力接近極限值時進行載荷調整。

在滿足以上控制要求的同時，以水平儀綜合水平度顯示作為評價標準。可以看出，調平過程狀態多樣，情況復雜，需要考慮協調多種影響因素，并反饋到控制策略中，實時檢測調整控制結果。

2 模型分析

可將圖1的12點支撐簡化為如圖3所示模型。1、2、3、4四點確定的平面中心點為O，實際中的芯級水平儀位置。在調平過程中，如若1、2、3、4四點確定的平面為水平面時，Ⅰ、Ⅱ、Ⅲ、Ⅳ象限的三點平面也為水平面，則12點共處于同一水平面中。

圖3 12點支撐簡化模型Fig.3 The Simplified Model Diagram of 12 Points Support

這樣模型可以拆分為2種簡單共面模型：四點支撐調平和三點支撐調平。

a）四點支撐調平。

將由4個獨立象限中1、2、3、4四點，也就是各象限主支承臂所在點位確定的平面記為芯級平面，如圖4所示。

圖4 芯級平面模型Fig.4 Core Level Plane Model Diagram

水平傳感器沿X、Y方向布置，X、Y兩個方向的水平傾角為α和β，兩傳感器間的夾角為γ，則平臺的傾斜角度θ可由α和β合成為[1]

在實際動作中，γ為90°，則公式可簡化為

b）三點支撐調平。

將各獨立象限中三點確定的平面記為跟隨平面，如圖5所示。

圖5 跟隨平面模型Fig.5 The Follow Plane Model Diagram

O點為象限的主支承臂，默認其為基準已根據式（1）模型調整水平，所以在三點支撐模型中無動作。水平面為過O點的調平平面。A、B兩點為象限內輔助支承臂，A′、B′為A、B兩點在水平面的映射。γ、θ為水平儀所測OAB平面與水平面兩垂直方向上的夾角。α、β為∠AOA'、 ∠BOB'。只需得到AA'和BB'的距離，便可得到各支臂的調整位移[2]。

設OA=OB=a，AC=BC=b，如圖5所示，則存在如下關系式：

可得：

3 方案分析

對理想的調平過程與要求進行分析可知，在實際的調平過程中，高度值需要實時監測并將情況進行反饋，才能進行下一步動作，力和水平儀作為檢測和判別的標準，其規律是需要通過反復試驗進行摸索的，將得到的規律加入到控制中有助于進一步的優化，所以提出的方案是以高度作為主要的調平控制對象。

在高度的控制過程中，主要通過對流量的調控，實現對支承臂升降的控制，從而達到對高度的實時監控。在這過程中，主要依據比例積分微分控制（Proportional Integral Derivative，PID）調節原理。

連續時間PID控制系統如圖6所示。圖中，D(s)為控制器。在PID控制系統中，D(s)完成PID控制規律，稱為PID控制器。PID控制器是一種線性控制器，用輸出量y(t)和給定量r(t)之間的誤差的時間函數。e(t)=r(t)-y(t)的比例，積分，微分的線性組合，構成控制量u(t)，稱為PID[3]。

圖6 連續時間PID控制系統Fig.6 Continuous time PID Control System

PID整定的理論方法：通過調整PID的3個參數KP、TI、TD，將系統的閉環特征根分布在s域的左半平面的某一特定域內，以保證系統具有足夠的穩定裕度并滿足給定的性能指標[4]。KP增大，系統響應加快，靜差減小，但系統振蕩增強，穩定性下降；TI增大，系統超調減小，振蕩減弱，但系統靜差的消除也隨之減慢；TD增大，調節時間減小，快速性增強，系統振蕩減弱，穩定性增強，但系統對擾動的抑制能力減弱。常見被控量的PID參數經驗選擇范圍如表1所示。

表1 常見被控制量PID參數經驗選擇范圍Tab.1 Empirical Selection Rang Table for PID Parameters of Common Controlled Quantities

本方案主要對液壓的輸出流量進行控制。采用試湊法確定PID調節參數：根據經驗范圍，設定基本的初值，通過模擬或閉環運行觀察系統的響應曲線，然后根據各環節參數對系統響應的大致影響，反復湊試參數，以達到滿意的響應，從而確定PID參數。反饋誤差參量為位移。建立公式模型如下：

標準腿作為基準，將其動作曲線認為是理想曲線；隨動腿作為跟隨，按照理想曲線調整。計算隨動腿和標準腿的變換高度誤差，將誤差δΔ反饋到隨動腿的流量控制中，反復調整得到最佳的輸出曲線。

4 試驗數據分析

根據第3節的方案分析，結合多點調平樣機試驗臺架進行了模擬試驗，試驗臺架實物分布如圖7所示。通過試驗來驗證方案的正確性，摸索多點調平的綜合控制策略，因此，下面對主要的3個影響因素（高度、載荷和水平度）。分別進行分析，綜合各個因素的影響程度，得到最終的綜合控制原則。

圖7 多點調平樣機臺架試驗實物Fig.7 Physical Drawing of Multi-point Leveling Prototype Bench Test

4.1 控制精度

試驗中，分別對4點同升同降、4點對角升降、12點同升同降、12點對角升降4種工作狀態進行模擬試驗。考慮到控制的輸出量，將KP初步設定為2，TI結合試驗中其對控制效果影響較小的實際情況，將其取為0。KP根據各隨動腿的距離比例分別進行設定。依照閥件特性，以輸出電流12 mA為中心零位，即液壓系統為0 L/min，動作死區范圍為[11mA，13mA]，默認無動作。電流值大于13 mA時支臂升；電流值小于11 mA時支臂降。

下面以加載10 t時12支臂對角2降4升試驗數據為例，進行分析討論。在該種工況下，載荷的均勻分布情況為主支承臂1176 N，輔助支承臂735 N。載荷超差范圍控制在各支承臂均勻承載情況下的50%。

a）方案初期，根據經驗值范圍選定系數KP為2，高度偏差、輸出流量變化曲線如圖8、圖9所示。

圖8 高度偏差Fig.8 Height Deviation Chart

圖9 輸出流量Fig.9 Output Flow Curve

b）當內圈四主支承臂KP為1，外圈的四輔助支承臂KP為2時，根據前期的試驗數據結果，調整參數KP的大小。高度偏差、輸出流量變化如圖10、11所示。

對比圖8、圖9與圖10、圖11兩組數據曲線可以看出，試驗前期將所有支臂的KP系數均設定為2時，PID的調節幅度較大，調節頻率較頻繁，并伴有某些支臂出現了反向穿越的情況；根據前期的數據結果，將在不同工況下的相對內側4個主支承臂的系數KP減小時，PID的調節幅度減小，頻度適中，消除了大部分的反向穿越現象，使得PID的調整效果更佳。

4.2 載荷規律

對單個支臂進行升降動作，以觀察分析單支臂動作對其他支臂的載荷產生的影響規律。

a）主支臂動作時（主支臂動作先后順序：3、4、2、1），載荷變化如圖12、圖13所示。

圖12 各主支臂載荷變化Fig.12 Load Variation Curve of Each Arm

圖13 各隨動支臂載荷變化Fig.13 Load Variation Curve of Each Arm

b）隨動支臂動作時（動作支臂與先后動作順序：5、7、9、11），載荷變化如圖14所示。

圖14 各支臂載荷變化Fig.14 Load Variation Curve of Each Arm

通過數據曲線圖，不難發現，單個支臂動作調整載荷時，有以下規律：

a）當動作支臂為主支承臂時，主要影響的首先是本象限內的2個輔助支承臂，其次是兩側象限的輔助支承臂，然后是對角象限的主支承臂，且這些受到影響的支臂載荷變化是與動作支臂呈現相反的趨勢。

b）當動作支臂為輔助支承臂時，其主要影響的是本象限內的主支承臂，且這些受到影響的支臂載荷變化是與動作支臂呈現相反的趨勢。

4.3 水平度

試驗過程中，當將平臺依據水平儀顯示調平后，再對單支臂做微小的載荷調整時，對綜合水平度的影響較小，在5″范圍之內。

4.4 控制策略總結

綜合上述分析，可以得到多點支撐下，垂直度調整的控制策略如下：

考慮到水平度在調平后，單支臂微小動作對其影響較小，在控制中以高度誤差值作為基本的控制反饋參數，兼顧載荷情況。在調平動作過程中，檢測載荷情況，設置報警程序，當載荷出現超差時，發出報警信號并暫停動作進行載荷調整；在調平過程中若載荷未出現超差報警，則直到動作結束后，再進行單支臂的載荷調整。但根據試驗顯示，在動作過程中，載荷基本在控制范圍內變化，滿足控制要求。

5 結束語

本文依據需求以高度作為調整控制對象，提出調平控制算法，試驗證明該算法能實時的調整控制支承臂動作速度，將誤差控制在要求范圍之內。方案能滿足設計要求，實現高精度閉環調平控制功能。本文基于設計方案的試驗結果，對多點調平下的多影響因素間相互協調，做了初步探討，總結了多影響因素下的控制策略及優先程度。本試驗是基于模擬臺架進行的，較于實際工程應用鋼性較強，在實際產品應用中效果會較試驗有所提高，試驗結果具有較強的工程應用性。