基于小波分解與二階灰色神經網絡模型結合ADF檢驗的短期負荷預測方法
祖光鑫,武國良,王國良,于 洋
(1.國網黑龍江省電力有限公司電力科學研究院, 哈爾濱 150030;2.國網黑龍江省電力有限公司哈爾濱供電公司, 哈爾濱 150036)
0 引 言
實現負荷預測是保證電力輸送能夠按照計劃進行,維持電網能量交換平衡的關鍵環節。電力市場穩定運行必須依靠負荷預測,同時負荷預測也是電力規劃的重要依據,負荷預測的精度越高,電力設備的利用率就越高,能量損耗就越低。現在的負荷預測方法主要有兩類:第一類為時間序列法等統計模型,它是在分析歷史數據固有特性的基礎上發展起來的;第二類為基于氣象因素或價格等相關因素的負荷預測模型,但量化不同氣候和荷載條件之間復雜的相互作用需要更多考慮,因此,該文使用第一種模型。
目前常用的負荷預測方法主要有時間序列法[1]、人工神經網絡法[2-3]、模糊預測法[3]、數據挖掘預測法[4]、極限學習機預測法[5]和灰色預測模型法[6-7]等。而在文獻[8]中,采用了一種全新的基于根軌跡的短期負荷預測方法,不僅保證了誤差收斂,且對擬合方式進行了探討。在文獻[9]中,以印度電力市場為研究對象,提出了基于極限學習機的短期電力負荷預測方法。文獻[10]中采用了一種基于反饋網絡與主成分分解的短期電力負荷預測模型。大數據理論被廣泛應用于文獻[11]和[12]的負荷預測模型中,提出了一種基于小波網絡的負荷預測模型。在文獻[13]中,通過 LSTM(long-short term memory)模型對用戶負荷進行點預測。
小波分解(wavelet decomposition,WD)方法在文獻[14-17]中得到了廣泛的研究,它可以減少序列的非平穩特征,提高預測精度。在文獻[14]中對母小波的選擇進行研究,在此基礎上,對載荷序列進行小波分解,并且將各分量分別建立模型[15-17]。針對最近的科研過程分析,在使用WD處理時間序列時出現了兩個問題:一是沒有確定WD水平的理論依據,二是缺乏預測高頻分量的能力。
針對第一個問題,該文提出了一種增強迪基-富勒(augmented Dickey-Fuller,ADF)檢驗的WD序列選擇方法。對于第二個問題,采用了基于二階灰色預測模型的負荷預測模型。為得到二階灰色預測模型的最優參數,采用神經網絡映射方法構建了二階灰色神經網絡預測模型[gray neural network forecasting model,GNNM(2,1)]。
1 基于ADF檢驗的WD
1.1 WD法
利用WD可以高效地分析非平穩和非線性信號。該文采用WD對負荷序列進行處理,可以減少負荷序列的非平穩性,并以此作為提高預測精度的依據。WD由式(1)所示
(1)
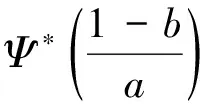
因此,對于與一個信號相關的所有a和b,所有小波系數WTx(b,a)的集合都與母小波相關,其中a和b是實數,表示復共軛。尺度參數a用于控制小波的擴展,平移參數b則決定小波的中心位置。
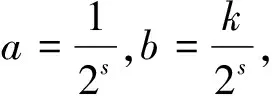
(2)
式中:Ψk,s(t)為離散小波基函數。
小波反變換由下式描述:
(3)
Mallat算法是一種基于多分辨率分析的小波變換快速算法。將載荷序列投影到尺度空間與小波子空間中,求出近似和的詳細信號。Mallat算法流程如圖1所示。
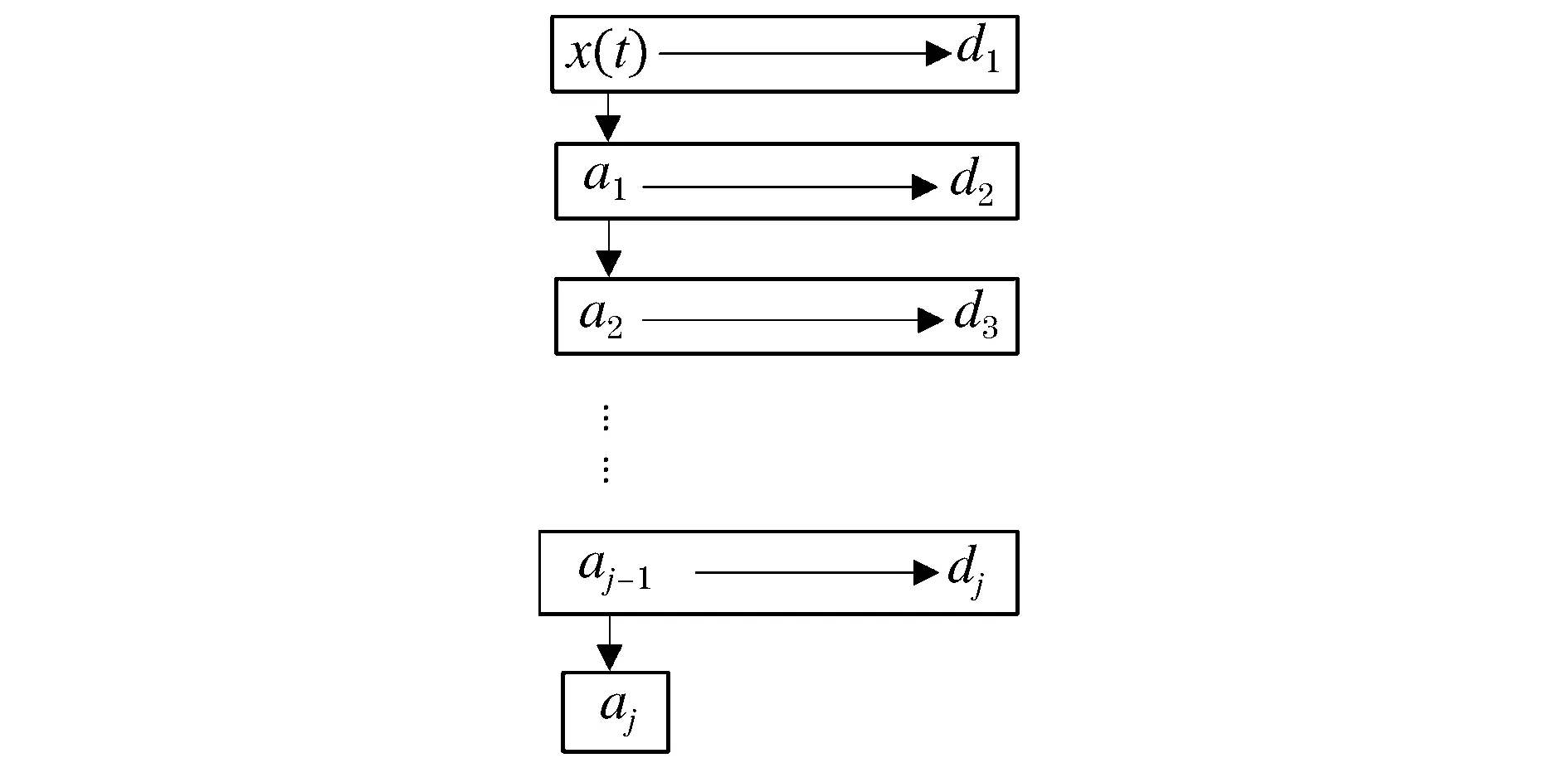
圖1 Mallat算法Fig.1 Mallat algorithm
分解過程可以表示為
(4)
式中:j表示Mallat算法的分解級別;H(·)為低頻分解函數,類似于低通濾波器;G(·)表示高頻分解函數,類似于高通濾波器。
在這個過程中,重構只需要系數向量,系數向量是通過將序列的長度降采樣為一半產生的。因此,重構前,需要對系數進行修正,在樣本之間分配零點。
(5)
式中:H*是H(aj)的對偶算子;G*是G(dj)的對偶算子。
這一過程完成后,負載序列x可通過消除高頻或將其分為高頻和低頻來平滑,該過程如下所示。
(6)
式中:Aj(t)表示近似信號或基元分量;Di(t)表示詳細信號或高頻分量。
為了得到二階灰色預測模型的最優參數,采用神經網絡映射方法構建GNNM(2,1)模型,重構各自輸出,得到最終預測負荷。
1.2 根據ADF檢驗確定最佳WD水平
分解層數和母小波的選取是影響預測結果的關鍵因素。該文對最優WD水平進行了研究。隨著分解水平的提高,低頻分量趨于穩定,基本分量的預測精度提高。然而,高頻分量的數量也增加了。因此預測的準確性隨著組件數量的增加而降低。故需要在WD水平和小波分量的穩定性之間找到一個平衡。
為了保證平衡,該文采用一種基于ADF檢驗確定最優分解水平的WD分組穩定性評價模型。ADF檢驗是單位根檢驗的一種改進方法。它的原理是檢查一個單位根是否在一個序列中出現。如果沒有單位根,則序列是平穩的,否則便是非平穩的。ADF檢驗通常用于評價經濟時間序列的平穩程度,通過ADF檢驗確定最佳WD水平步驟如下所述:
1)設j=1;
2)對負荷序列進行j級小波變換,求出各個分量;
3)用ADF法評價WD各組分穩定性;
4)如果每個部件都是穩定的,j是最好的WD水平,否則,j=j+1,重復步驟(2)。
利用這種方法,可以提高預測的準確性,得到WD的最優層。
2 灰色模型
灰色系統理論的特征是利用灰色數學處理不確定性,充分利用已知參數尋找系統的規律。基于灰色系統理論的預測模型具有模型簡潔易懂、所需歷史參數少、預測精度高、便于計算、不計分布特點等好處。GM(N,M)是階數為N,變量個數為M的灰色模型。二階灰色模型GM(2,1)共有兩個特征值,體現單調變化和非單調變化。計算結果可以很好地模擬出具有顯著振蕩特性的低頻分量和高頻分量。因此,該研究采用GM(2,1)模型。
2.1 GM (2,1)
歷史荷載數據經小波分解后的分量如下:
X(0)=[x(0)(1),x(0)(2),…,x(0)(n)]
(7)
式中:n是序列的個數。
將這些序列疊加產生新的序列,定義為1-AGO [使用上標“(1)”],即
X(1)=[x(1)(1),x(1)(2),…,x(1)(n)]
(8)
x(1)(n)定義為
(9)
基于一階累積生成操作建立二階微分模型,如下式所示:
(10)
這個方程的解如下:
(11)
式(11)為λ1和λ2預測值的解析表達式,揭示了λ2+a1λ+a2=0特征方程的特征根。最后,我們使用以下式獲得最后的預測結果。
x(0)(t)=x(1)(t)-x(1)(t-1)
(12)
2.2 灰色神經網絡模型(GNNM)
灰色模型的參數計算一般采用最小二乘估計法,這需要更新計算結果。想要加快模型的訓練速度,減少計算時間,就需要進行大量的計算。同時,為了提高計算效率,利用最小二乘估計方法對灰色模型的初始值進行估計。最后通過訓練灰色神經網絡,得到最優模型參數。
采用最小二乘估計法計算初始值來確定式(10)中a1、a2、b的初始值(灰色神經網絡的初始權值),公式如下所示:
(13)
其中:
z(1)(t)=0.5x(1)(t)+0.5x(1)(t-1),t=2,3,…,n
參數C1和C2由下面的推導得到,可用一階差分替換積分項如:
(14)
對(11)中的t求導,即

(15)
將式(15)代入式(14)可得
x(0)(t)=C1λ1eλ1t+C2λ2eλ2t
(16)
參數C1和C2通過求解(11)和式(16)得到。為了構造GNNM,將式(11)進行如下變換
(17)
根據(17)構造神經網絡圖,如圖2所示。
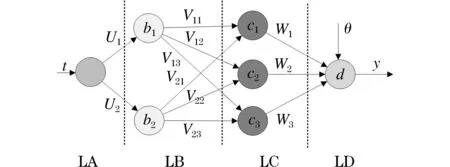
圖2 GNNM(2,1)網絡原理圖Fig.2 Schematic diagramof the GNNM (2,1) network
得到模型的最優參數,神經網絡的學習過程遵循以下過程。
步驟1:輸入初始權值[見式(13)~(16)]和網絡閾值。
U=[U1U2]=[λ1λ2]
W=[1+eλ1t1+eλ1t1+eλ2t]T
LD層的閾值表示為
步驟2:計算每一層的輸出。
LB神經元的輸出定義為
LC神經元的輸出定義為
c1(t)=V11b1(t)
c2(t)=V12b1(t)
c3(t)=V23b2(t)
LD神經元的輸出定義為
d(t)=y1(t)=W1c1(t)+W2c2(t)+W3c3(t)
步驟3:計算逆誤差。
LD層誤差定義為
δd=y(t)-y1(t)
式中:y(t)是實際數據。
LC層誤差定義為
δc1=δdW1;δc2=δdW2;δc3=δdW3
LB層誤差定義為
步驟4:更新權重和閾值。
ΔU和ΔV分別為U和V的修正權值,η為學習速率,μ為慣性系數。
ΔU1(s)=μΔU1(s-1)+ηδb1t
ΔU2(s)=μΔU2(s-1)+ηδb2t
ΔV1(s)=μΔV1(s-1)+ηδc1t
ΔV2(s)=μΔV2(s-1)+ηδc2t
ΔV3(s)=μΔV3(s-1)+ηδc2t
矩陣V的剩余修正量為零,s表示訓練次數。
U(s+1)=U(s)+ΔU(s)
V(s+1)=V(s)+ΔV(s)
矩陣W更新如下:
W1=W2=1+eU1t;W3=1+eU2t
步驟5:重復步驟2~4,直到達到收斂條件。
完整的算法流程如下圖所示:
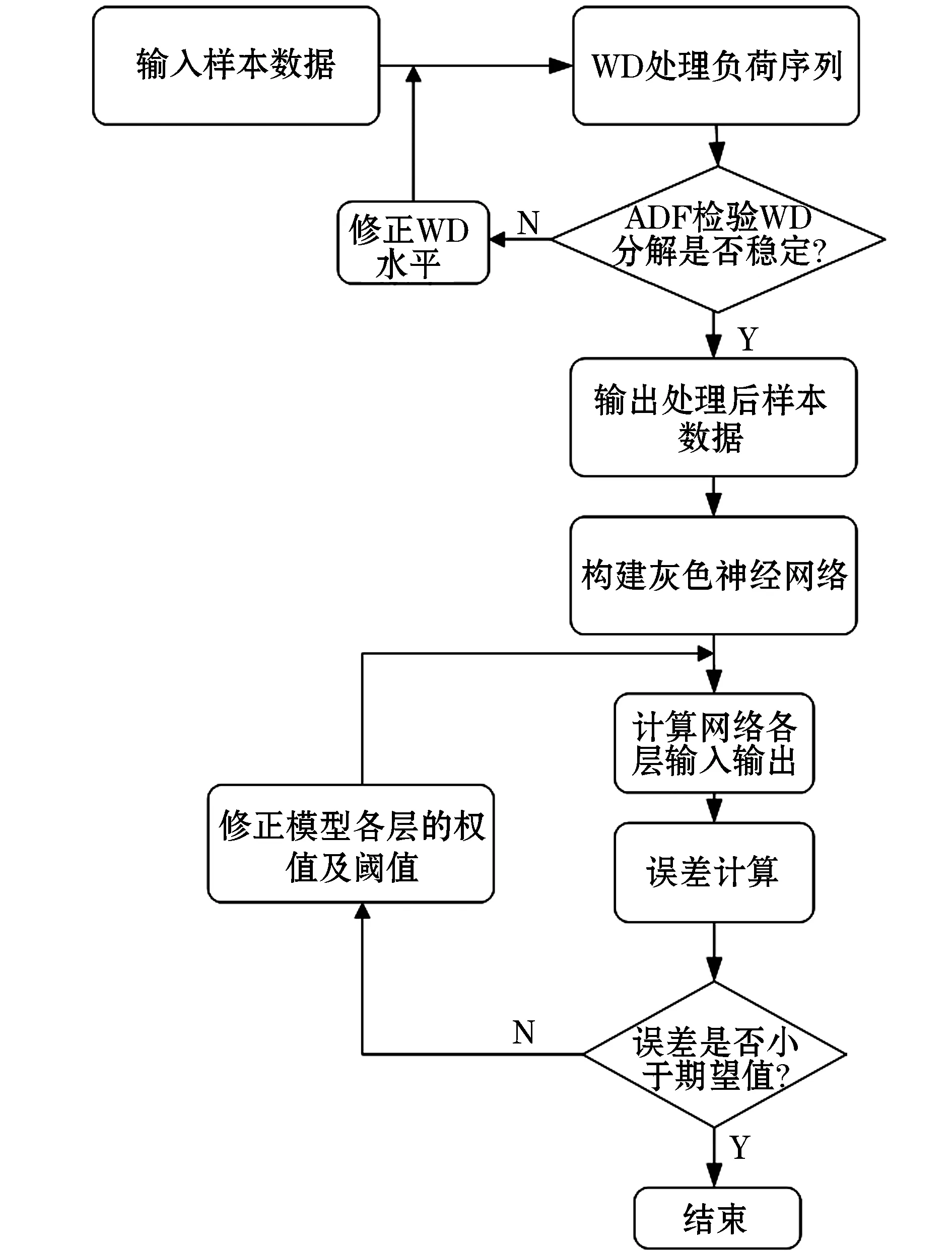
圖3 程序流程框圖Fig.3 Program flow diagram
3 案例研究
3.1 歷史數據
以中國西南某變電站2016年連續負荷時間間隔為1 h的1 000個數據點為研究對象。采用樣本中前900個測量數據用來訓練,后100個測量數據用來測試。圖4為樣本圖示。
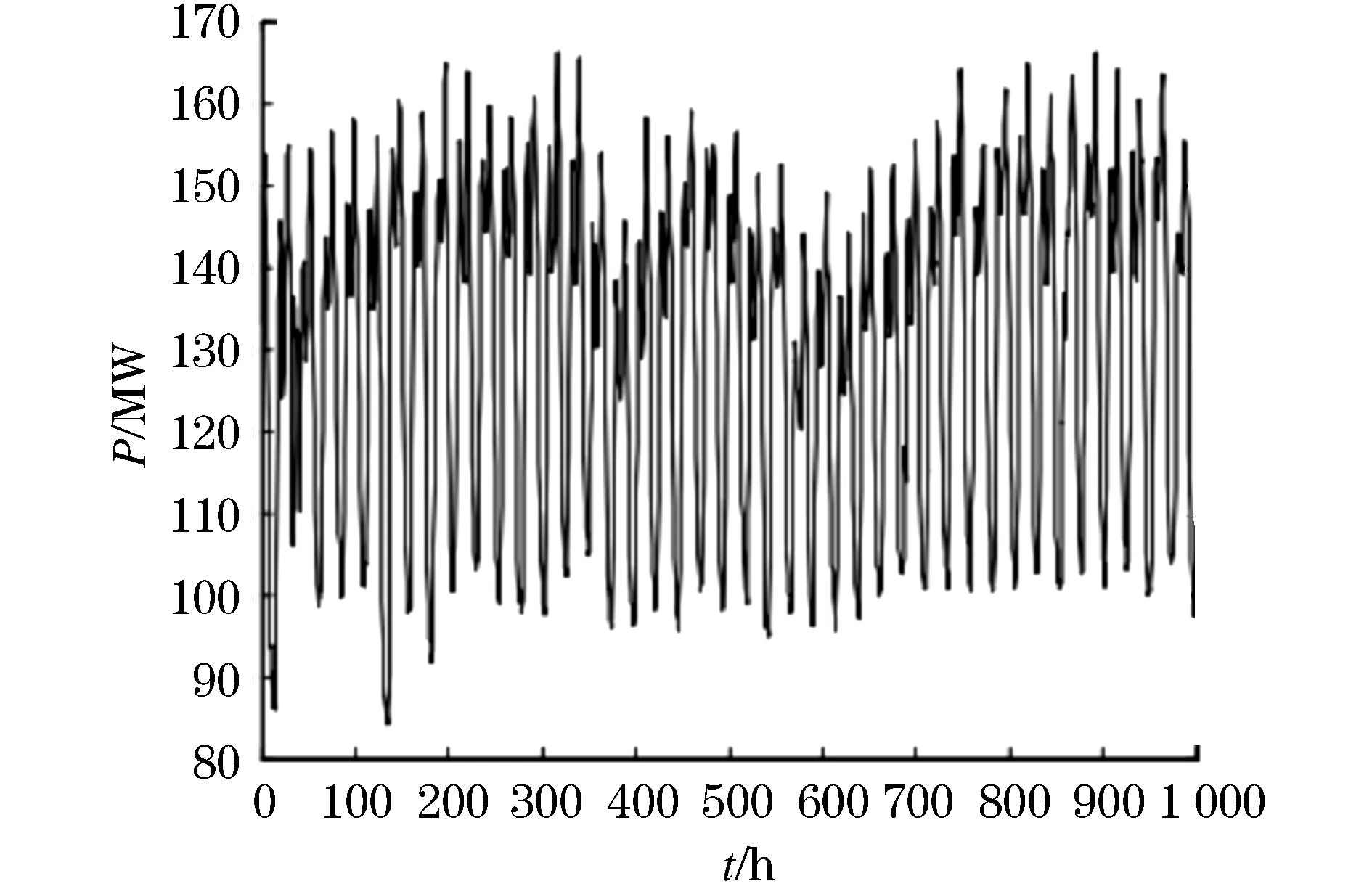
圖4 負荷時間序列Fig.4 Load time series
現有的一些利用小波變換進行電力負荷預測的研究,通常采用四階Daubechies小波。從ADF檢驗中,我們選擇WD級別為5。設給定長度為N的信號為s,離散小波變換至多包含log2n個階段,樣本最多分解9層,圖5表示按頻率分解的電負荷。
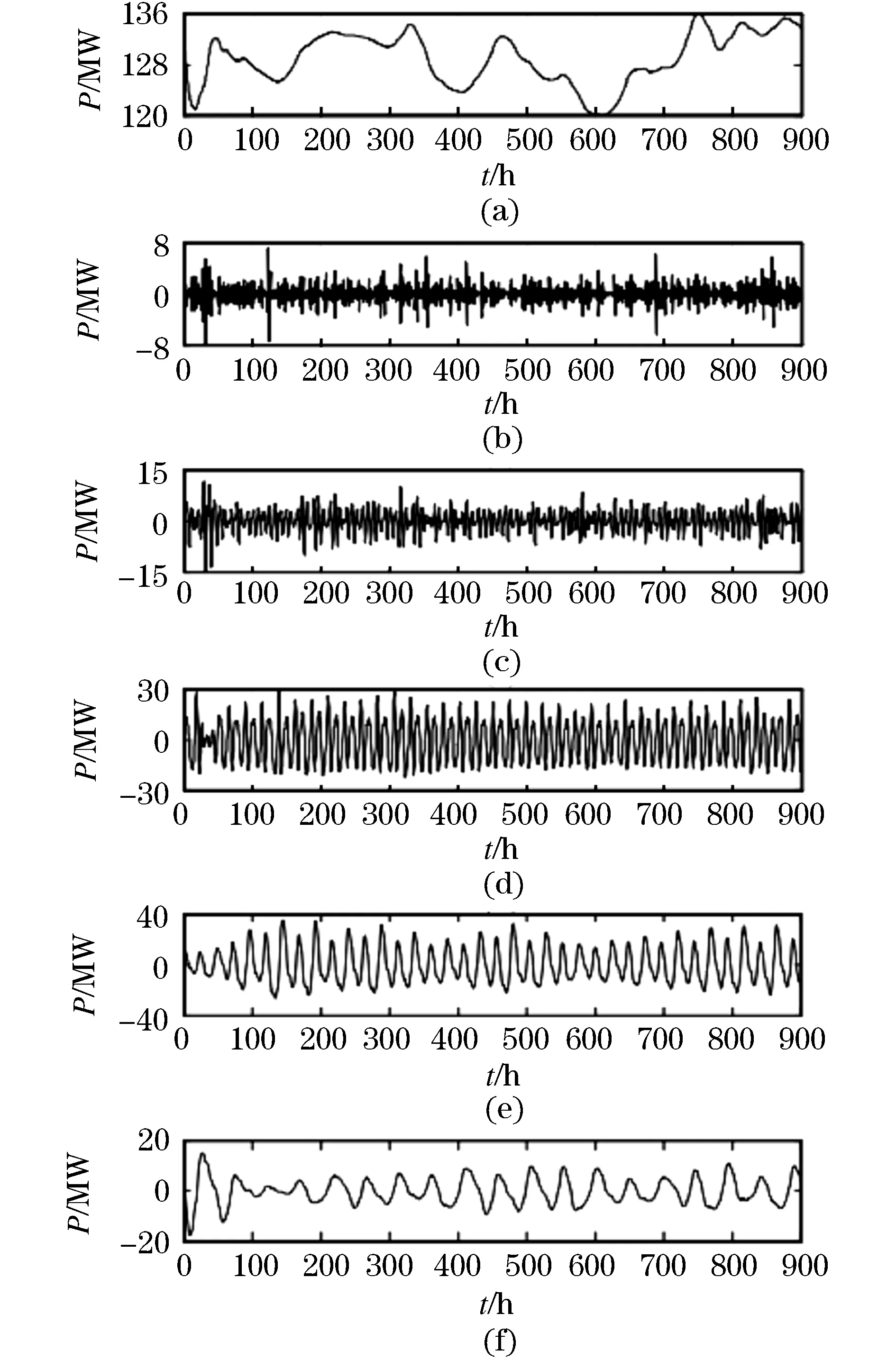
圖5 利用離散小波變換對電力負荷進行分解Fig.5 Decomposed electric load using discrete wavelet transform
3.2 預測結果
應用WD各分量的二階灰色神經網絡模型[GNNM(2,1)]清楚地顯示了基于WD的預測結果,如圖6所示。使用WD-Elman(五層WD結合Elman神經網絡)和GNNM(2,1)比較所提出的WD GNNM(2,1)的性能。圖7表示負荷預測結果及不同模型的結果。
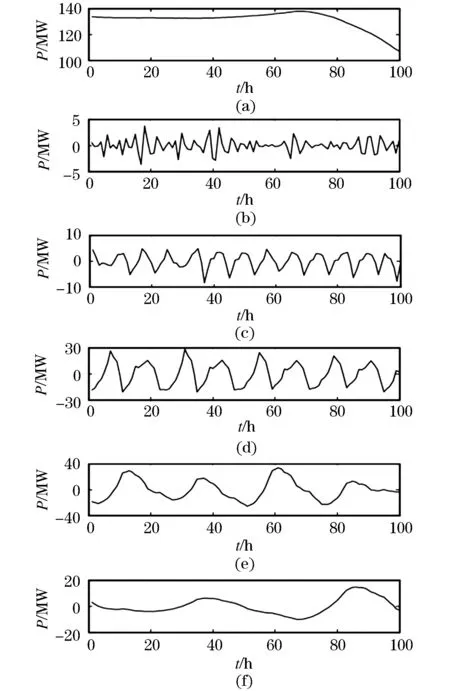
圖6 基于各分量WD-GNNM(2,1)的預測結果Fig.6 Forecasting results based on WD-GNNM (2, 1) of each component
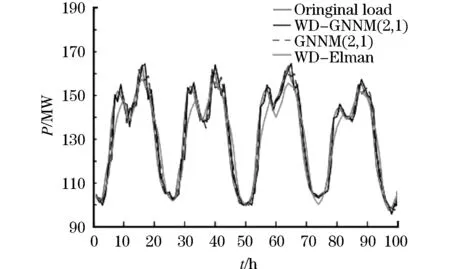
圖7 不同模型的負荷預測結果Fig.7 Load forecasting results of different models
3.3 結果分析
為了驗證ADF檢驗以確定WD的最優層,單層WD到九層WD基于ADF檢驗的穩定性結果列于表1。使用平均絕對百分比誤差(mean absolute percentage error,MAPE)來評估我們的結果。表2列出了不同時期的計算映射。
(18)
式中:y′(i)為預測值;y(i)為實際數據;N為序列個數。
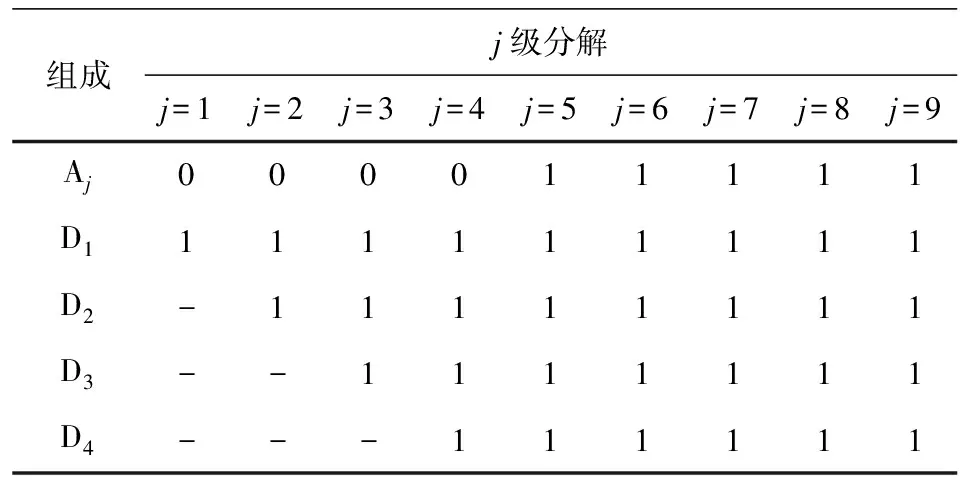
表1 ADF的測試結果Table 1 ADF test results
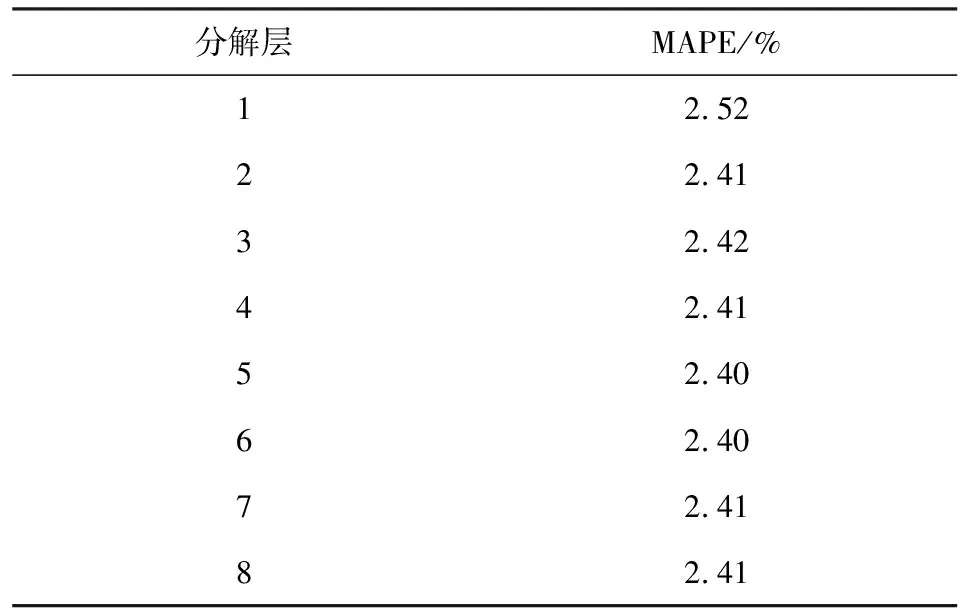
表2 不同分解層的MAPE指數Table 2 MAPE index of different decomposition layers
在表1中,0表示序列為非平穩狀態,1表示序列為平穩狀態。在單層WD中,A1為非平穩分量,D1為平穩分量。繼續分解A1,求出兩層WD的結果;然而A2仍然是一個非平穩分量。隨著Aj的不斷分解,各成分在五層WD中變得穩定。從表2可以看出,隨著WD層數的增加,誤差減小。在五層WD中,基本分量是平穩分量。此時累積誤差最小。當分解水平大于5時,由于各分量都是穩定的,因此保證了各分量的預測精度。然而,隨著WD的推進,累積誤差逐漸增大。
表3和圖7給出了該文提出的WD-GNNM(2,1)和其他兩種方法的詳細誤差分析。理論分析和試驗評價表明,所提出的WD-GNNM(2,1)是一個最優解,有利于建立高精度的負載模型,證明了WD可以提高預測精度。

表3 MAPE指數的不同方法Table 3 Different methods of MAPE index
4 結 語
該文提出了一種基于WD的二階灰色神經網絡短期負荷預測方法,WD后各分解分量的平穩性采用ADF檢驗。首先,小波變換可以降低負荷序列的非平穩性,提高預測精度。其次,基于ADF檢驗確定最優WD水平的方法能夠在最優WD水平與小波分量穩定性之間找到平衡,預測誤差降到最低,最后所提出的WD-GNNM(2,1)能有效提高預測精度。

