面向生產車間的單車路徑優化算法研究

陳澤宇，馮子驍，宋佳員

（1.河海大學機電學院，江蘇 常州213022；2.河海大學物聯網學院，江蘇 常州213022）

1 引言

自動引導小車（Automated Guided Vehicle，AGV）在20 世紀50 年代被首次提出。作為一種智能搬運設備，由于其自動化程度高、易于控制等優點，廣泛應用于倉儲、物流行業。在一些加工車間內，使用AGV 來搬運物料，能有效節約勞動成本和提高工作效率，因此對AGV 應用的研究極為重要，其中如何設置AGV 的路徑直接影響企業生產效率和成本，需要對其進行深刻研究。

目前求解AGV 最優路徑主要采用的是人工智能的算法，比如蟻群算法[1-2]、粒子群算法[3]、神經網絡算法[4]、快速擴展隨機樹尋路算法[5]以及遺傳算法[6-7]。這些有群體智能的算法都有正反饋機制和較優的擴展性，在路徑規劃和旅行商問題（TSP）[8-10]中被成功應用。文獻[1]中使用了優化后的蟻群算法，相較于傳統算法避免了尋優的盲目性，從而提高了算法效率。文獻[3]中使用三角函數變化方式對其參數進行自適應調整，并加入雞群算法去除擾動，有效避免了算法停滯。文獻[4]采用的是基于神經網絡算法來規劃機器人移動路徑，縮短了搜尋時間。而其中遺傳算法雖然提出時間較早，但是由于其是多點式搜索，更有可能搜索到全局的最優解，所以如今多數路徑規劃問題仍可以用遺傳算法去求解。但是傳統的遺傳算法有自身固有缺點，比如容易早熟、收斂效果差的缺點，因此，在使用時必須對其進行改進。本文提出的改進型遺傳算法，是在傳統遺傳算法基礎上，對其中交叉和變異過程進行優化，提高算法計算效率，縮短計算時間，獲得更好的搜索結果。

2 模型建立

對于研究AGV 的路徑規劃問題，首先要建立合適的地圖模型，常用的方法有可視圖法[11-12]、傳統柵格法[13]和人工勢場法[14-15]。其中柵格法（grid method）具有簡單、易于表達和靈活等優點，所以本文采用柵格法建立AGV 地圖模型。如圖1 所示，黑色區域表示障礙或者機器，白色區域AGV可以行駛，行駛方向為AGV 所在格的周圍八個柵格。此外，此柵格可以坐標化便于之后遺傳信息的編寫和路徑長度計算。本文之后的算法都在此柵格地圖的基礎上進行求解。

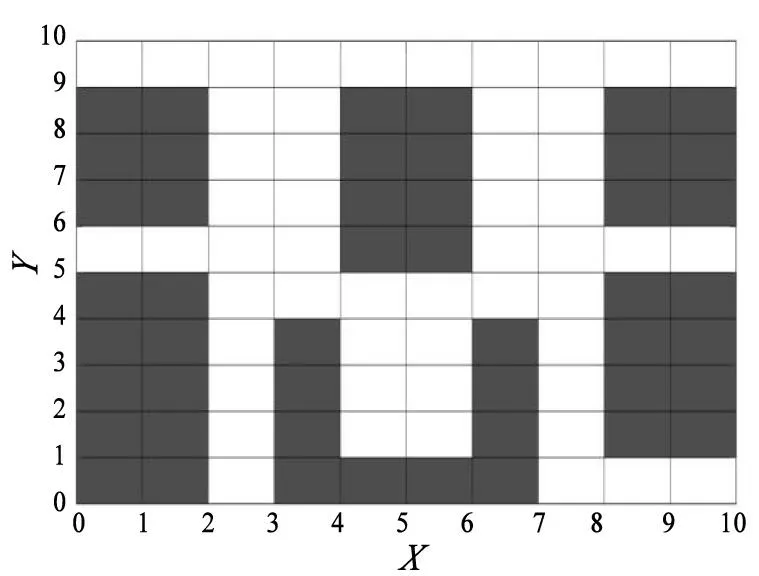
圖1 地圖柵格模型

3 改進型遺傳算法

3.1 改進型遺傳算法模型

遺傳算法是模擬達爾文進化論所創建的，根據生物遺傳和進化的特點和步驟，引入了基因復制、交叉突變等遺傳信息的處理方式，并且采用了進化論中適者生存的法則，對基因信息進行篩選。

本文提出的改進型遺傳算法來求解最優路徑，首先會產生第一代中會產生多條路徑，記為1iL。其中，下標i表示第一代的第i條路徑，上標為代數，路徑由構成路徑的坐標點構成，從點按順序排布，每一條路徑都能代表一個遺傳信息，如式（1）所示。

對于第一代所有路徑的集合記為C1，其中C1表示為：

之后計算C1中的長度，記為，表示為：

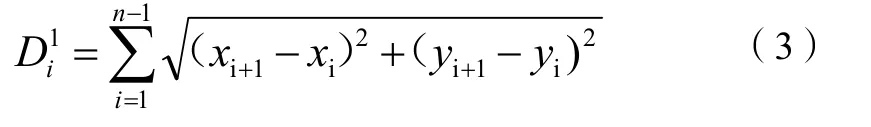
比較之后選出這一代中路徑長度最短的一組遺傳信息，將其路徑長度作為之后評估的標準。

在獲取第一代信息后，對遺傳信息進行復制，準備下一步基因交叉和突變。復制時，根據每一條路徑的長度和最短路徑的比值確定對應遺傳信息的比值后設置一個復制閾值P0，如果比值低于這個閾值，則該遺傳信息不進行復制，但這個值不能取太大，太大容易快速進入局部最優，損失部分可交換的遺傳信息，所以選擇合適的閾值有利于提高算法求解速度，且能提高算法的收斂性。

遺傳信息復制結束后需要對信息進行重新結合，也就是“交叉重組”。交叉重組旨在擴大搜索范圍，產生新品種的后代，為之后迭代復制提供資源，隨著復制過程中的篩選體現出優勝劣汰的特點。該操作的過程是將已經復制的遺傳信息進行部分互換，找到兩組遺傳信息中共用的坐標點，對其進行前后段互換，即可得到一個新的遺傳信息，擴大遺傳算法的搜索。具體先任選一個信息設為，然后算出該信息與其他信息之間的路徑的距離如式（4）所示。

i

0

i

按照此概率選擇方式完成一對信息配對后，將所有信息都進行同樣的操作，之后對每一對信息組中的公共點隨機選擇作為交叉節點，互換遺傳信息，完成一次“交叉重組“操作，得到第二代遺傳信息

3.2 改進型遺傳算法流程

基于以上算法描述，得到改進型遺傳算法的基本流程如下：①獲取第一代所有的遺傳信息，即初始信息集合；②對信息集合中每一條遺傳信息進行計算評估，根據其評估值和閾值的對比，判斷信息是否有繼續遺傳下去的必要，如果沒有則去除此信息，如果有則進行下一步；③復制選擇后的遺傳信息，作為交叉重組的基礎；④使每一條遺傳信息根據概率公式配對、重組，得到新一代信息集合；⑤判斷是否到達最大迭代數，若是則輸出最優路徑，算法結束，若不是則重復步驟②～④，直到算法結束。

4 仿真分析

在MATLAB 軟件中對改進型遺傳算法進行了仿真實驗，在25×25 的柵格地圖的背景下進行計算，總共設置100次迭代，每一代中有50 條遺傳信息，計算結果顯示改進型遺傳算法在算法求解時間和收斂效果上均與傳統算法相比有提升。

圖2 為通過改進型遺傳算法求解出的AGV 最短運動軌跡圖。表1 為改進型遺傳算法和傳統的遺傳算法的對比數據，每種算法各在相同情況下運行10 次后求平均值。

圖2 AGV 最短路徑軌跡

在兩種算法所需計算時間方面，由表1 數據可知，改進型遺傳算法由于在復制時提前進行篩查排除一些極差遺傳信息，減去了大量后期交叉重組所需要的時間，減少了一定的計算量，使得計算時間由平均13.862 9 s 縮短至12.684 7 s，減少了8.49%。

在兩種算法所解最短路徑長度方面，由于改進型算法在引入了概率計算和去除極端信息時，有助于算法收斂，所以改進型遺傳算法的最短路徑為38.627 4，而傳統遺傳的最短路徑為39.974 1，且10 次平均下來改進型遺傳算法也要優于傳統算法，體現出改進后算法的優良性質。

表1 算法性能對比

5 總結

對于傳統遺傳算法在求解AGV 最短路徑規劃問題時的一些不足，在傳統算法的基礎上，我們增加了遺傳信息復制階段的評估篩選和交叉重組階段的概率配對，以此來縮短算法計算時間和提高算法的收斂性。最后的仿真結果也證明了改進型遺傳算法有優于傳統遺傳算法之處。